基于马尔科夫状态转移模型的天气衍生品定价
杨刚 杨徐


摘 要 引入马尔科夫状态转移(MRS)模型拟合长沙市每日平均气温变化,利用最大期望算法估计马尔科夫状态转移模型参数,通过误差分析得到了最佳MRS模型.基于最佳的MRS模型,采用无套利定价原理定价气温衍生品,并利用蒙特卡罗方法得到了取暖指数(HDD)欧式看涨期权的数值解.实证结果表明,五状态的MRS模型对长沙市每日平均气温变化的拟合效果明显优于其他的MRS模型,它使得气温衍生品定价结果相比以前的方法更为精确.
关键词 数量经济学;最优气温模型;EM算法;无套利定价原理;天气衍生品;MRS模型
中图分类号 F840.67 文献标识码 A
Abstract The Markov regime-switching model is introduced to fit the variation of Changsha daily average temperature. The parameters of Markov regime-switching (MRS) models are estimated by Expectation-Maximization algorithm. The optimal MRS model is derived by error analysis. On the basis of the optimal MRS model, no-arbitrage pricing principle is applied to pricing the temperature derivatives. Numerical solution to the HDD European call option is determined by Monte Carlo method. As the empirical result is shown, the fitting effect of five-state-MRS model for the variation of Changsha daily average temperature is superior to other MRS models. Hence, the pricing result of temperature derivatives is more accurate than ever.
Key words quantitative economics; optimal temperature model; EM algorithm; no-arbitrage pricing principle; weather derivatives; MRS model
1 引 言
自1997年12月84個国家在日本京都签订《京都协议书》以来,人们日益认识到气候变化对生产生活的严重影响,并且把该年定为天气衍生品交易元年.2014年8月,国务院发布了《关于加快发展现代保险服务业的若干意见》,指出要“探索天气指数等新兴产品和服务”.天气风险通常分为巨灾天气风险和非巨灾天气风险.对于巨灾风险,许多学者已进行了深入研究.杨刚等(2008)[1]通过Esscher变换对巨灾超额损失再保险进行定价,沈明轩和何朝林(2012)[2]假定巨灾指数服从分数跳扩散情形,利用保险精算方法定价巨灾期权.天气衍生品是一种基于天气指数的未定权益,它通常用于管理因不利天气变化造成的经济损失,常见标的包括温度、降雨量、降雪量和霜冻天数等天气指标.
由于天气衍生品的标的不可交易,天气衍生品市场属于不完全市场,因此不能应用经典的Black-Scholes期权定价方法对天气衍生品进行定价.现有的天气衍生品定价方法种类多样,主要包含精算定价方法、无套利定价方法、效用无差异定价方法和均衡定价方法(Lee和Oren,(2010)[3]).传统的精算定价方法通常基于精算等价原则,往往采用真实概率测度得到贴现价格,由于天气衍生品市场存在显著的风险市场价格,故容易导致较大的定价误差.效用无差异定价方法和均衡定价方法通常以效用函数为基础,由于对个人效用函数的选取较为主观,所以容易产生较大的定价误差.选取风险中性定价方法确定气温衍生品的无套利价格比较合理,它是一种灵活而又便于实施的金融衍生品定价方法.
在无套利定价方法中,Alaton等(2002)[4]首次引入布朗运动驱动的O-U过程对气温衍生品进行无套利定价.王明亮等(2015)[5]利用布朗运动驱动的O-U过程拟合北京市每日平均气温变化,通过蒙特卡洛方法定价气温衍生品.王晶(2016)[6]利用布朗运动驱动的O-U过程拟合北京市每日平均气温变化,通过有限差分方法得到气温期权的数值结果.胡亚茹(2019)[7]采用布朗运动驱动的O-U过程拟合哈尔滨、北京等五个城市的每日平均气温变化,通过蒙特卡洛模拟得到气温期权价格.Alaton等(2002)[4]采用常数方差刻画气温的波动,Benth等(2007)[8]采用截断的傅里叶级数描述方差变化的时变结果,Li(2018)[9]对布朗运动驱动的O-U模型进行改进,采用偏微分方程(PDE)定价天气衍生品.Benth等(2005)[10]发现气温残差并不完全符合正态分布的假定,这使得气温衍生品在定价过程中存在较大的误差,所以他们采用lvy过程驱动的O-U过程来拟合气温过程的变化轨迹.Elias等(2014)[11]首次将两状态马尔科夫状态转移模型(Markov regime-switching, MRS)模型应用于气温衍生品定价.随后,Evarest等(2017)[12]对两状态MRS模型进行拓展,提出时变波动率MRS模型.Gyamerah等(2018)[13]在Evarest等(2017)[12]的工作上对MRS模型进一步修正,得到lvy过程驱动的两状态MRS模型.Xiong和Mamon(2018)[14]采用受隐马尔可夫链调制的O-U过程对天气衍生品进行定价.MRS模型在一定程度上提升了天气衍生品定价的精确性,同时也增加了计算的复杂性.通过对不同气温模型对比分析,最终采用MRS模型对气温衍生品进行无套利定价.
受Evarest等(2017)[12]和Gyamerah等(2018)[13]提出的两状态MRS模型启发,进行了两方面的拓展,一是将时变波动率均值回复MRS模型中基本状态的时变波动率拓展到带有常数指数时变波动率的MRS模型;二是将两状态的MRS模型拓展到五状态的MRS模型.同时,基于最优的MRS模型对取暖指数(heating degree days,HDD)期权进行无套利定价,并通过蒙特卡罗方法得到了HDD期权价格的数值解.
2 每日平均气温分解和马尔科夫状态转移模型
通过分解得到每日平均气温的残差,并用MRS模型拟合每日平均气温残差的变化.
3 气温模型数值分析
首先描述數据来源和数据特征,然后对方程(2)的参数使用非线性最小二乘法估计.最大期望算法(Expectation-Maximization algorithm,EM)以极大似然估计方法为基础,较为简便也便于操作,算法收敛的稳定性强,采用EM算法对MRS模型的参数进行估计应该是可行的.基于所有的MRS模型,拟合气温数据并使用误差分析,挑选最优的MRS模型以便于下一节对气温衍生品进行定价.
3.1 数据来源与数据特征描述
气温数据来源于美国海洋和大气管理局(NOAA)美国海洋和大气管理局官网(https://www.ncdc.noaa.gov/data-access/quick-links#dsi-3505).
将气温衍生品应用于农业天气风险管理之前,需要对气温衍生品进行定价.由于气温衍生品用于管理农业天气风险可能存在地理基差风险,而减少基差风险的简便方式是选取覆盖地点较近的气温衍生品合约.因此选取长沙站点作为湖南省具有代表性的气象站点,时间区间为2016年1月1日到2019年12月31日,样本数量为1461个.在此研究的气温衍生品是以长沙市每日平均气温数据为标的的气温衍生品.需要注意的是,基于长沙市每日平均气温指数的气温衍生品的价格数值并不一定与采用其他地区的气温数据得到的价格数值一致,原因是不同地区的气温数据存在差异,但仍然可以采用与此相同的模型、方法和步骤得到其他地区的气温衍生品的价格.由于样本量较大,可能存在缺失数据的情形.对缺失数据的处理,详见Alexandridi和Zapranis(2012)[16].表1中描述性统计呈现长沙每日平均气温特征,表明样本数据不服从正态分布,并且波动性较大.
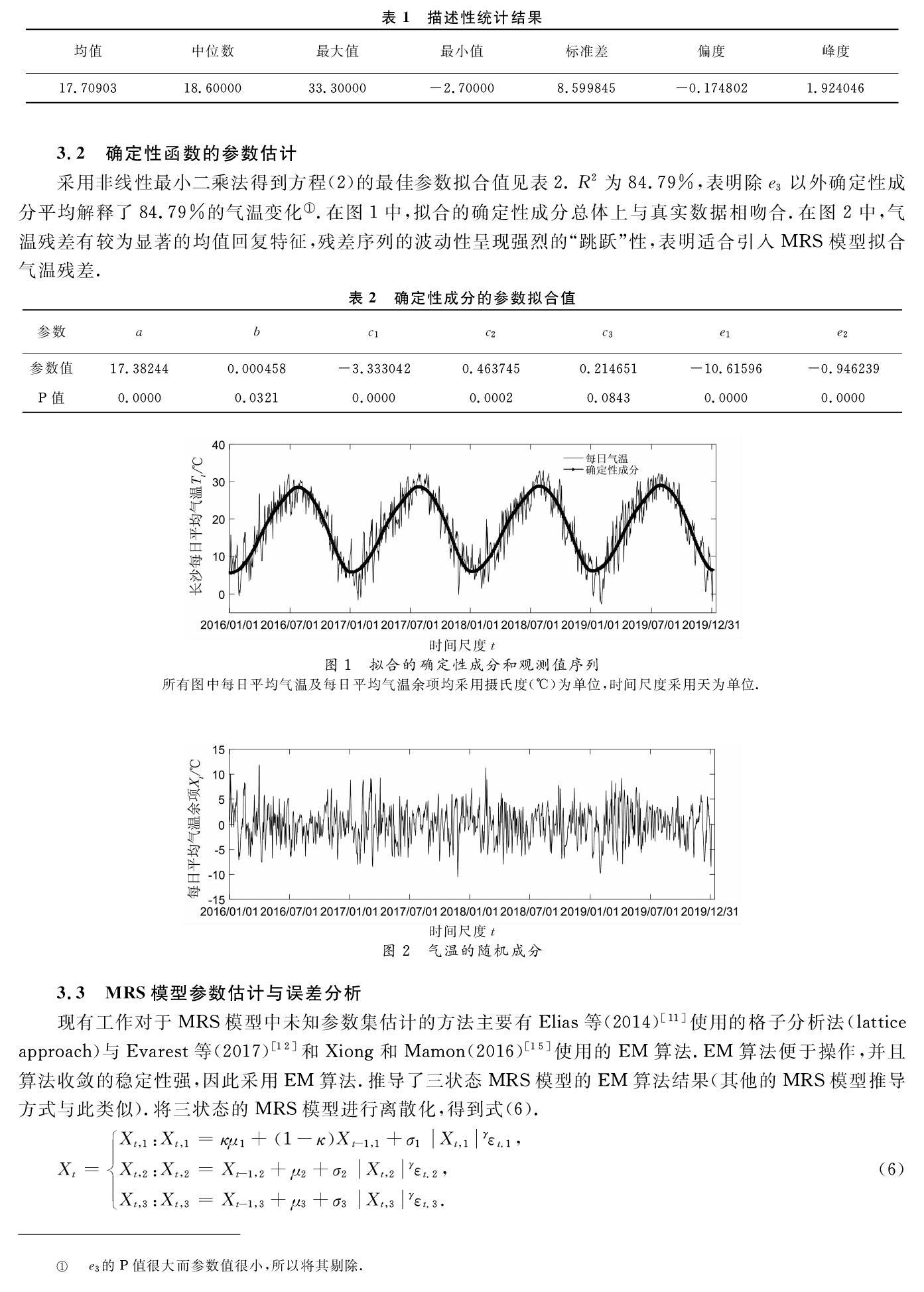
3.2 确定性函数的参数估计
采用非线性最小二乘法得到方程(2)的最佳参数拟合值见表2.R2为84.79%,表明除e3以外确定性成分平均解释了84.79%的气温变化e3的P值很大而参数值很小,所以将其剔除..在图1中,拟合的确定性成分总体上与真实数据相吻合.在图2中,气温残差有较为显著的均值回复特征,残差序列的波动性呈现强烈的“跳跃”性,表明适合引入MRS模型拟合气温残差.
5 结 论
通过将Evarest等(2017)[12]和Gyamerah等(2018)[13]MRS模型的时变波动率拓展到带常数指数的时变波动率MRS模型,将两状态的MRS模型拓展到五状态的MRS模型,发现MRS7模型对长沙市每日平均气温残差的拟合效果相对较好.五状态MRS模型优于其他的MRS模型.在气温期权定价的数值结果中,存在气温风险市场价格和不存在气温风险市场价格两种情形下得到的期权价格相差较大,在气温期权定价时,需要考虑风险市场价格,这与Xiong和Mamon(2018)[14]的研究结果一致.
在高状态MRS模型的拓展中,并未使用lvy过程作为“跳跃”状态构建MRS模型,这可能使得某些极端异常气温难以被模型拟合,未来可以构建常数指数时变波动率均值回复过程为基本状态、lvy过程为“跳跃”状态的MRS模型.
参考文献
[1] 杨刚,刘再明,欧阳资生,等.隐含风险中性分布在巨灾超额损失再保险定价中的应用[J].经济数学,2008,25(4):331-337.
[2] 沈明轩,何朝林.分数跳扩散环境下的巨灾期权定价[J].经济数学,2012,29(3):78-81.
[3] LEE Y, OREN S S. A multi-period equilibrium pricing model of weather derivatives[J],Energy Systems,2010,1(1):3-30.
[4] ALATON P, DJEHICHE B, STILLBERGER D. On modelling and pricing weather derivatives[J].Applied Mathematical Finance, 2002, 9(1):1-20.
[5] 王明亮,何建敏,陈百硕,等.时变O-U模型在气温预测及气温期货定价中的适应性研究——基于北京市1951-2012年的日平均气温数据[J].中国管理科学,2015,23(2):44-49.
[6] 王晶.天气衍生品定价模型的构建[J].统计与决策,2016,32(15):152-155.
[7] 胡亚茹.基于O-U模型的气温衍生品定价研究[J].武汉金融,2019,36(4):31-35,71.
[8] BENTH F E, ALTYT-BENTH J. The volatility of temperature and pricing of weather derivatives[J].Quantitative Finance, 2007, 7(5):553-561.
[9] LI P. Pricing weather derivatives with partial differential equations of the Ornstein-Uhlenbeck process[J]. Computers & Mathematics with Applications, 2018, 75(3): 1044-1059.
[10]BENTH F E,ALTYT-BENTH J. Stochastic modelling of temperature variations with a view towards weather derivatives[J].Applied Mathematical Finance, 2005, 12(1):53-85.
[11]ELIAS R S, WAHAB M I M, FANG L. A comparison of regime-switching temperature modeling approaches for applications in weather derivatives[J]. European Journal of Operational Research, 2014, 232(3): 549-560.
[12]EVAREST E, BERNTSSON F, SINGULL M, et al. Regime switching models on temperature dynamics[J].International Journal of Applied Mathematics and Statistics, 2017, 56(2):19-36.
[13]GYAMERAH S A, NGARE P, IKPE D. Regime-switching temperature dynamics model for weather derivatives[J].International Journal of Stochastic Analysis, 2018,32(1):1-15.
[14]XIONG H, MAMON R. Putting a price tag on temperature[J]. Computational Management Science, 2018, 15(2): 259-296.
[15]XIONG H, MAMON R. A self-updating model driven by a higher-order hidden Markov chain for temperature dynamics[J]. Journal of Computational Science, 2016, 17(1): 47-61.
[16]ALEXANDRIDIS A K, ZAPRANIS A D. Weather derivatives: modeling and pricing weather-related risk[M].New York:Springer Science & Business Media,2012.
[17]HAMILTON J D. Analysis of time series subject to changes in regime[J]. Journal of Econometrics, 1990, 45(1/2): 39-70.
[18]XIONG H, MAMON R. A higher-order Markov chain-modulated model for electricity spot-price dynamics[J].Applied Energy, 2019, 233(1): 495-515.

