基于等效初始裂纹尺寸的吊杆疲劳寿命预测
马亚飞,欧阳清波,汪国栋,王磊,张建仁
(长沙理工大学 土木工程学院, 湖南 长沙 410114)
吊杆是中、下承式拱桥和悬索桥的重要受力构件,长期处于高应力状态。在环境和荷载等因素作用下,若防护不当,高强钢丝易发生腐蚀[1]。腐蚀会加速材料的疲劳损伤过程,显著降低吊杆的疲劳寿命[2]。吊杆腐蚀疲劳失效往往是无任何征兆的脆性破坏。在中国,已发生多起因吊杆疲劳断裂导致的安全事故。许多学者已对高强钢丝的疲劳性能进行了研究。李晓章[3]等人开展了不同腐蚀程度高强钢丝的疲劳试验,发现锈蚀会大幅降低钢丝的疲劳寿命。Nakamura[4]等人采用不同缺口类型来模拟钢丝表面的腐蚀形态,指出钢丝局部缺陷是导致其疲劳性能退化的主要原因。Ma[5]等人建立了应力范围-疲劳寿命-缺口深度的关系模型。但采用的自制缺口与实际锈蚀形态存在着一定的差别。在疲劳寿命评估方面,李先立[6]等人采用偏度-峰度法研究了不同应力水平下高强钢丝的疲劳寿命,得到了Weibull分布下高强钢丝概率寿命曲线和疲劳强度。Castillo[7-8]等人考虑应力幅值的影响,提出了高强钢丝疲劳寿命评估的多参数Weibull 模型。Lan[9]等人基于锈蚀钢丝应力-寿命曲线和线性损伤累积方法,建立了平行钢丝疲劳寿命概率分析模型。线性损伤累积方法计算简单,但缺乏明确的物理失效准则。一些学者基于断裂力学和裂纹增长分析,对高强钢丝疲劳寿命进行了研究。Toribio[10]等人对比了不同直径钢丝疲劳裂纹速率的差异。马亚飞[11-12]等人开展了平行钢丝顶推试验,采用光学观测方法,得到了不同应力比下高强钢丝的疲劳裂纹增长分析模型。然而,受观测手段的限制,未得到门槛值附近的裂纹扩展速率。郑祥隆[13]等人建立了适用于不同屈服强度和应力比的疲劳裂纹扩展模型,但忽略了锈蚀发展对钢丝疲劳的影响。这些研究均针对单根钢丝,单根钢丝断裂并不意味整根吊杆失效。因此,作者基于等效初始裂纹原理,拟将蚀坑引起的应力集中融入应力强度因子表达式中,建立高强钢丝疲劳寿命预测模型。考虑钢丝的串并联关系和断丝后应力重分布的影响,通过引入关联系数分析吊杆内各钢丝疲劳寿命的相关性,提出服役桥梁吊杆疲劳寿命评估方法,并进行参数敏感性分析,以期为大跨度桥梁吊杆的安全性评价和维护提供参考。
1 高强钢丝疲劳裂纹扩展
疲劳裂纹的萌生和发展规律是疲劳寿命预测的前提。疲劳裂纹增长曲线分为低速扩展、稳定扩展和裂纹失稳区[14],稳定扩展区是决定疲劳裂纹扩展寿命的主要区域。材料裂纹扩展速率的计算式[15]为:

式中:a为裂纹长度;ΔKth为疲劳裂纹扩展门槛值;ΔK为应力强度因子幅值;N为疲劳寿命;C和m均为与应力比相关的常数。
为研究应力比的影响,进行了不同应力比下高强钢丝疲劳裂纹扩展速率试验[11],得到了C和m的表达式。
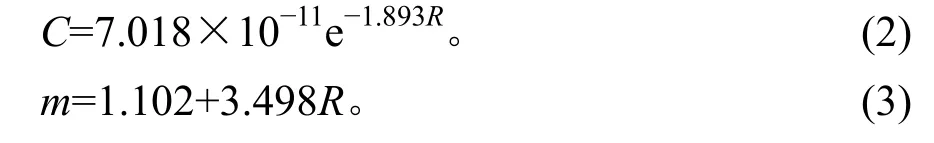
式中:R为应力比。
对式(1)进行积分,可得:

式中:ai为材料初始裂纹长度;ac为临界裂纹长度。
为避免复杂的短裂纹增长分析,一些学者提出了采用等效初始裂纹进行疲劳寿命预测[16]。目前,等效初始裂纹尺寸(equivalent initial flaw size,简称为EIFS)有3 种计算方法[17]:①外推法:通过调整初始裂纹的大小使数值模拟下的理论寿命接近试验结果,由此来估算等效初始裂纹尺寸。②TTCI法:从试验获得裂纹扩展深度与循环次数曲线或裂纹扩展深度与时间关系曲线,将N=0(或t=0)所对应的裂纹扩展深度视为等效初始裂纹尺寸。③Kitagawa-Takahashi 图法:利用裂纹长度与疲劳应力幅的关系,将等效裂纹初始尺寸视为材料的一种固有特性,如图1 所示。

图1 Kitagawa-Takahashi 图法Fig.1 Kitagawa-Takahashi method
Liu[18]等人给出EIFS 的计算方法,其表达式为:

式中:Δσf为疲劳极限;Y为几何修正因子,取决于裂纹扩展前沿形状。
已有研究[11]表明:钢丝疲劳裂纹前缘形状在初始扩展阶段呈半圆形。随着裂纹的扩展,裂纹前缘的形状逐渐趋于扁平。裂纹前沿的几何修正因子为:

式中:D为钢丝直径。
材料屈服强度σy与疲劳裂纹扩展门槛值Kth受显微组织的影响,二者存在对应关系。对珠光体钢丝的门槛值进行了统计,建议门槛值经验公式[13]为:

式中:σy为屈服强度。
实际环境中,钢丝发生锈蚀后,蚀坑处应力集中效应明显,降低了钢丝的疲劳寿命。腐蚀钢丝应力集中系数的计算公式为:

式中:d为锈坑深度。
蚀坑尖端的应力强度因子[19]可表示为:

式中:Kt为应力集中因子;σ为远端应力。

图2 锈坑深度与裂纹深度增长示意Fig.2 Schematic of pit depth and crack depth growth
当钢丝疲劳裂纹发展至临界尺寸时,则发生断裂,临界裂纹长度ac与材料的断裂韧度Kc有关,其计算公式[20]为:

式中:σmax为最大应力;Kmax为应力强度因子上限值。
Mahmoud[21]发现:当裂纹长度与钢丝直径比值达到0.5 时,钢丝发生断裂。因此,ac与直径D的关系可表示为:

2 吊杆疲劳寿命预测
桥梁吊杆由J根平行钢丝组成,其最大应力为σmax,最小应力为σmin,应力比为:

若吊杆防护套的有效防护时间为T年,年车辆荷载循环次数为Q,则T年的荷载循环次数为QT,通过QT可求得积分上限a1。

吊杆护套出现破损后,有害介质进入并诱发腐蚀,钢丝锈坑深度为:

式中:b为年锈坑深度增量;t为腐蚀时间。
考虑腐蚀的影响,吊杆内单根钢丝的疲劳寿命为:
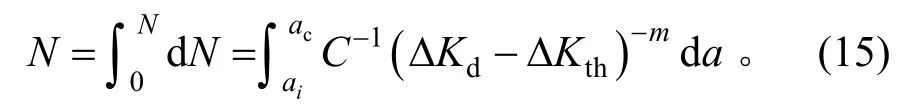
疲劳裂纹尺寸a1作为疲劳寿命积分下限,将年荷载循环次数代入公式,可求得第T+1 年疲劳寿命积分上限a2。

同理,将疲劳裂纹扩展尺寸a2作为第T+2 年疲劳寿命积分下限,将此时锈坑深度代入公式,求得第T+2 年疲劳寿命积分上限a3。

依此类推,计算得到a4,a5,…,an。裂纹长度达临界长度时,钢丝发生疲劳失效,其疲劳寿命为:

若各根钢丝互不关联,考虑断丝后应力重新分布的影响,则:

式中:σfmax为应力重分布后的最大应力;σmax为初始最大应力;J为吊杆内钢丝总数;M为断丝数。
由式(13)~(19)可得到,考虑应力重分布影响的服役吊杆内每根钢丝的疲劳寿命Ni。本研究引入关联系数分析吊杆内各钢丝疲劳断裂的相关性,吊杆疲劳寿命可表示为:

式中:φi,i+1为第i根钢丝与第i+1 根钢丝的关联系数,假定φi,i+1~U[0,1];Ng为吊杆疲劳寿命。
3 实例分析
某三跨连续中承式钢管混凝土拱桥主桥为(80+368+80) m,主拱拱肋为无铰支。吊杆间距为8 m,由73 根屈服强度为1 670 MPa 的镀锌高强钢丝组成。锚头采用OVM-LZM 型冷铸镦头锚,吊杆钢丝的总横截面积为2 807.95 mm2,如图3 所示。建立该桥的有限元分析模型[22],对吊杆内力进行了计算。其中:受力最大的吊杆轴力Fmax为2 254.40 kN,最大应力σmax为802.86 MPa,最小轴力Fmin为1 887.36 kN,最小应力σmin为672.15 MPa,应力比R为0.84。

图3 平行钢丝吊杆断面示意Fig.3 Schematic of parallel wire bundle
对该桥吊杆进行评估前,需得到护套随时间的破损模型。目前,PE 护套按有关试验数据推断其防腐寿命约为25 a,但实际统计结果发现吊杆3~5 a需进行防腐维修,10~15 a 需将原有涂层全部去除[23]。本研究取护套有效防护时间为10 a。防护套出现破损后,钢丝每年锈坑深度增加0.5 mm,假定该桥日荷载循环为500 次,由高强钢丝疲劳裂纹扩展模型考虑钢丝的串并联关系和断丝后吊杆钢丝应力重分布,将相关参数代入式(18)和(19),依次计算出N1,N2,…,Ni。采用蒙特卡罗方法抽样1×105次,根据式(20)可计算得到考虑钢丝间相关性的吊杆疲劳寿命Ng。断丝率ξ为吊杆疲劳寿命评估的重要指标。不同断丝率下吊杆疲劳寿命的预测结果见表1。吊杆疲劳寿命可用正态分布来描述,即:吊杆循环次数的均值、标准差及变异系数。相应的概率密度函数如图4 所示。
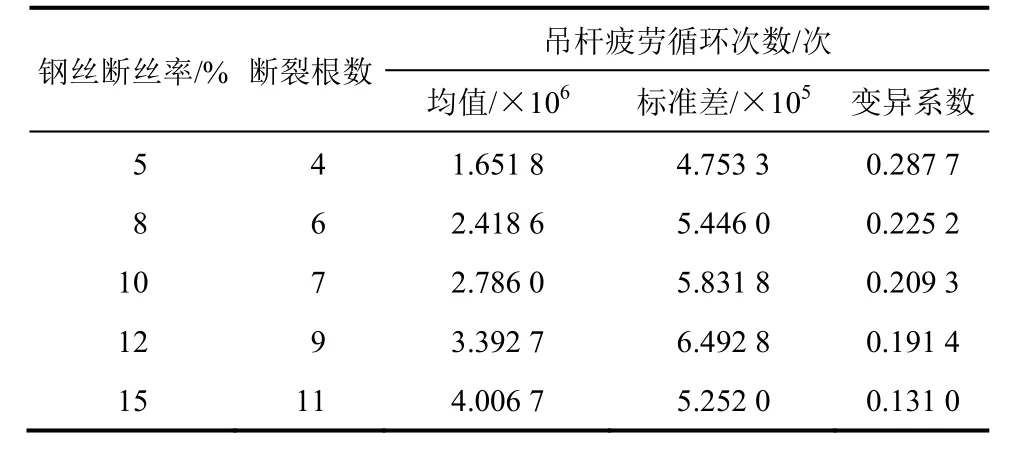
表1 断丝率与吊杆疲劳寿命Table 1 The broken wire rate and fatigue life of suspender

图4 不同断丝率下吊杆疲劳寿命的概率密度Fig.4 PDF of fatigue life of suspender under various wire failure rate
从表1 和图4 中可以看出,断丝后吊杆应力幅增大,断丝速度加快,引起钢丝疲劳寿命进一步降低。随着断丝率的增加,概率密度曲线逐渐右移。当断丝率由5%提高至8%,10%,12%和15%时,吊杆疲劳循环次数均值分别增加了7.668×105,1.134 2×106,1.740 9×106和2.354 9×106次,标准差逐渐增大。按照《斜拉桥用热挤聚乙烯高强钢丝拉索(GB/T 18365—2018)》[24]规定,拉索在2×106次脉冲疲劳循环后,断丝率不大于5%。本试验结果表明:当断丝率ξ等于8%时,吊杆所经受的疲劳循环次数均值为2.419×106次,仍满足规范2×106次循环的要求。
不同地区荷载频率和环境存在差异,应考虑荷载频率和蚀坑增长速度等因素的不确定性,进行参数敏感性分析,探讨各参数对预测结果的影响程度,如图5 所示。从图5(a)中可以看出,日均荷载频率从500 次/d 增加至1 000 次/d 时,疲劳寿命均值增加了33.9%,但吊杆服役时间减少了33.1%。腐蚀的不确定性主要体现在锈坑形状和腐蚀速率方面,锈坑增长速率对吊杆疲劳寿命的影响如图5(b)所示。随着锈坑增长速度的增加,概率密度曲线左移,吊杆疲劳寿命逐渐减小,曲线变陡,标准差逐渐减小。当锈坑年增幅从0.5 mm/a 增加至1 mm/a 时,疲劳寿命均值减少了28.4%,其服役时间减少了28.6%。表明荷载频率的变化对疲劳寿命更为敏感。
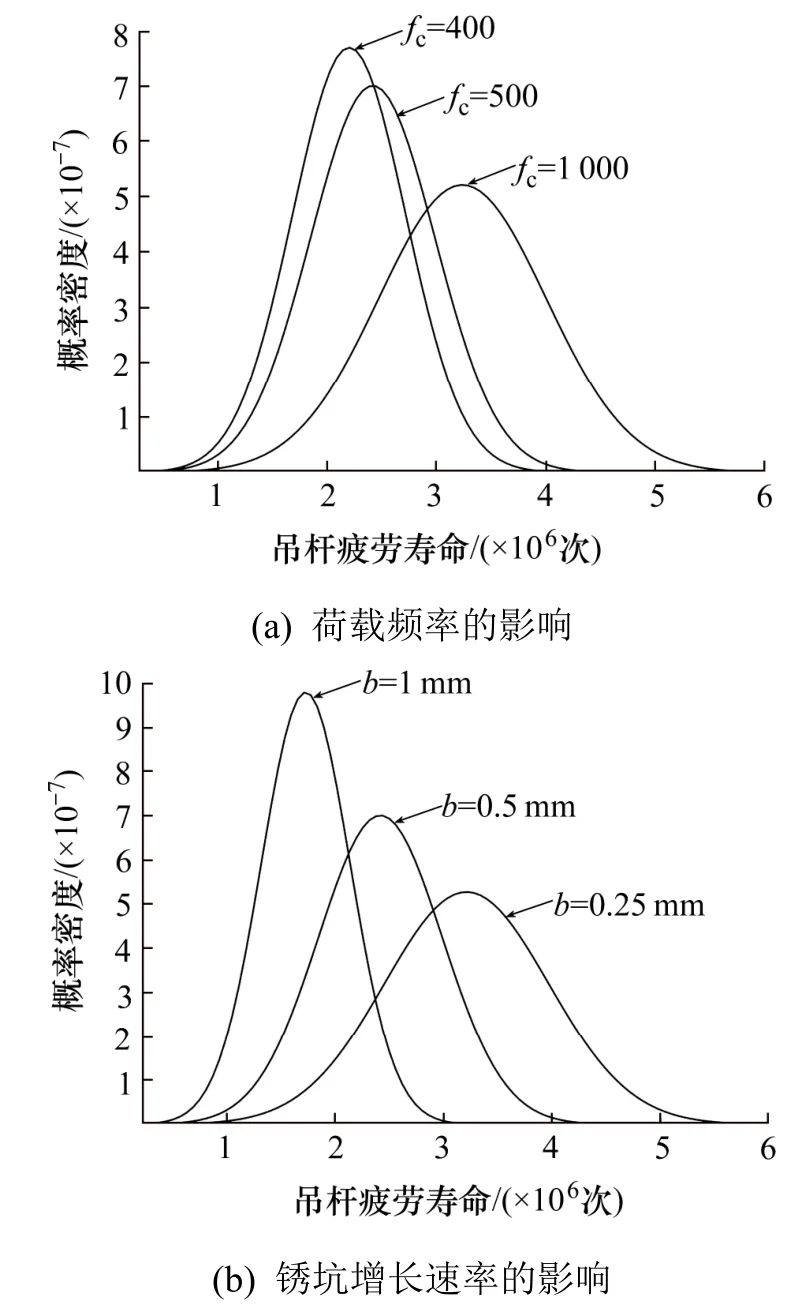
图5 参数对吊杆疲劳寿命的影响Fig.5 Influence of parameters on the fatigue life of suspender
4 结语
基于等效初始裂纹尺寸原理,将锈坑引起的应力集中融入应力强度因子表达式中,建立了高强钢丝疲劳寿命预测模型。考虑钢丝的串、并联关系和断丝后应力重分布的影响,引入钢丝间断丝的关联系数,分析吊杆内各钢丝疲劳寿命的相关性,提出了服役桥梁吊杆疲劳寿命评估方法,并依托一座服役实桥进行了验证分析。得出的结论为:
1) 蚀坑增长速度和荷载频率对吊杆疲劳寿命的影响显著;与蚀坑增长速率相比,荷载频率对疲劳寿命更为敏感。
2) 该研究可为吊杆使用寿命评估和失效标准提供依据,也可为相关管理部门限载提供参考。
3) 实际中,疲劳损伤较为复杂,疲劳荷载往往为随机荷载,如何考虑随机荷载的影响仍需深入。另外,假定的吊杆内各钢丝疲劳断裂的关联系数,其适用性仍需日后进一步验证。

