轴向导热对换热管及壳程圆筒壁温影响的理论分析与数值模拟

聂毅强

(中国石化工程建设有限公司,北京100101)

管壳式换热器换热管内轴向导热和壳程圆筒内导热在传热过程中普遍存在,由于对传热影响较小,在传热研究和设计中,一般较少考虑.但在一些特殊情况下,如反应器飞温、反应气“前烧”或“尾烧”以及反应产物快速降温,一概地忽略这些热传导,不仅研究和设计不完整,还有可能导致较大的计算误差.因此,有必要对这些热传导进行研究.

换热管内轴向导热会改变换热管内部及表面温度,因而对换热管平均壁温、管内及管外流体有效温差和传热系数的计算产生影响;壳程圆筒内导热也同样会改变筒体内部及表面温度,但更少有研究.

夏新林【1】等人研究了管外冷凝且温度恒定时,忽略轴向导热导致的传热系数计算误差以及不同传热管材质对轴向导热的影响;王玮【2G8】等人研究了壁面轴向导热对微细换热管传热的影响;杨卫胜【9】等人研究了轴向导热对管式固定床反应器操作的影响;陈骁【10】等人研究了管壁厚和管内径之比对轴向导热的影响;李隆键【11】等人研究了传导面积及轴向导热对高温换热设备管口区传热的影响.

换热管和壳程圆筒壁温是换热器强度设计的关键参数.GB/T 151—2014«热交换器»未考虑轴向导热的影响.本文重点研究轴向导热对换热管及筒体壁温的影响.通过理论分析,得到轴向导热的影响因素和判定轴向导热影响大小的公式;通过数值模拟方法,得到轴向导热的影响范围和对换热管和壳程圆筒壁温的计算偏差,为换热管和筒体壁温的严格分析提供参考依据.

1 物理模型和控制微分方程

对管壳式换热器进行如下假设:

1)传热过程是稳态的;

2)单管程、单壳程且换热管内、外对流传热系数为常数;

3)管程、壳程流体在横截面上充分混合;

4)壳程流体沿轴向流动.

假设4)的目的是忽略筒体内的周向热传导.

根据上述假设,对稳定、无内热源、轴对称并考虑轴向导热的筒体及换热管可列出控制微分方程,并用柱坐标形式表达,有(式中符号说明见文末,下同):

作为求解式(1)的边界条件,可取筒体两端和外表面绝热,而筒体内表面为第三类边界条件,即

考虑筒体外与环境热交换时,有

作为求解式(2)的边界条件,可取换热管两端绝热,而管壁内、外表面为第三类边界条件,即

对管外流体,其热平衡方程式为:

对应的边界条件为:

对管内流体,其热平衡方程式为:

对应的边界条件为:

2 轴向导热影响因素分析

由于换热管内同时存在径向导热和轴向导热,因此根据式(2)直接求解换热管内轴向温度梯度比较困难.本文旨在给出换热管横截面上平均轴向温度梯度的影响因素和估值范围.根据理论和工程经验可知,径向导热比轴向导热大得多,故先不考虑轴向导热.取换热管上相邻较近的两个横截面“1－1′”和“2－2′”,如图1所示.

设管外为冷流体且流体热容量小于等于管内流体热容量,即

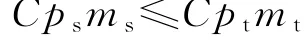
图1 温度截面

根据热平衡,有

也可写成

即,2－2′截面径向温度梯度更大一些,因此有

整理得

将式(9a)~式(9c)的每一项均除以Δz,整理得

忽略管外流体与筒体的换热,式(5a)可写成

式(6a)可写成

ξ1和ξ2分别是介于截面1－1′和2－2′之间、管外和管内传热面上的一点,该处径向温度梯度使得式(11)和式(12)成立.

式(10)可写成

当式(13)中Δz→0时,中间两项可以写成换热管外、内管壁的轴向温度梯度,ξ1和ξ2也趋向于z1.去掉z的下角标,写成

这就得到了管内、外壁轴向温度梯度与径向温度梯度之间的关系.

当Cpsms≥Cptmt时,式(15)中的“≥”改为“≤”.

式(15)给出了不考虑轴向导热、用换热管内壁和外壁径向温度梯度表示的换热管横截面上平均轴向温度梯度的估值范围.由于轴向导热总是倾向于减小轴向温度梯度,因此实际换热管横截面上平均轴向温度梯度接近甚至小于式(15)的下限.

一般情况下,换热管轴向温度梯度小于换热管内、外表面径向温度梯度的10%.极端情况下,当管内和管外流体质量流量和比热容的乘积很小、换热管内径和外径很大或者换热管导热系数很高时,换热管轴向温度梯度可能大大提高.典型工况是在高温、高真空条件下流体流量很低时的传热.

由于换热管导热系数在各个方向相等,因此,将式(15)左右同乘导热系数λt,就是换热管轴向热通量与径向热通量之间的关系.

换热管轴向导热的影响可以用轴向导热的传热速率与径向传热速率的比值η表示,仍按照Cpsms≤Cptmt,有

由式(16)可知,换热管导热系数越大、换热管横截面积越大以及管长越短、流体质量流量和比热容的乘积越小,换热管轴向导热影响就越大,反之则越小.

在常规条件下,换热管轴向导热负荷往往不到总传热负荷的0．1%,可以忽略不计.

换热管内轴向导热会改变换热管内部及内、外表面温度,因而对换热管平均壁温、管内及管外流体有效温差和传热系数的计算有影响.从宏观传热上讲,换热管内轴向导热会将热流体高温段热量传给低温段的冷流体,造成热量从高温到低温的“漏流”,并导致局部和总体传热温差均减小,对传热不利.

下面对壳程圆筒轴向导热进行研究.当认为筒体外侧与环境绝热时,由于筒体只有内表面与外界有换热,且筒体各点温度处于稳态,故沿筒壁长度对筒体内表面的传热进行整体积分,有

管外流体T(0)≠T(L)时,易得出如下结论:1)高温段流体向筒体传热,低温段筒体向流体传热;

2)筒体表面温度与对流系数乘积的积分值与管外流体主体温度与对流系数乘积的积分值相等.

式(18)为考虑筒体外表面向环境散热时,表达筒体横截面上平均轴向导热梯度的方程.推导过程略.

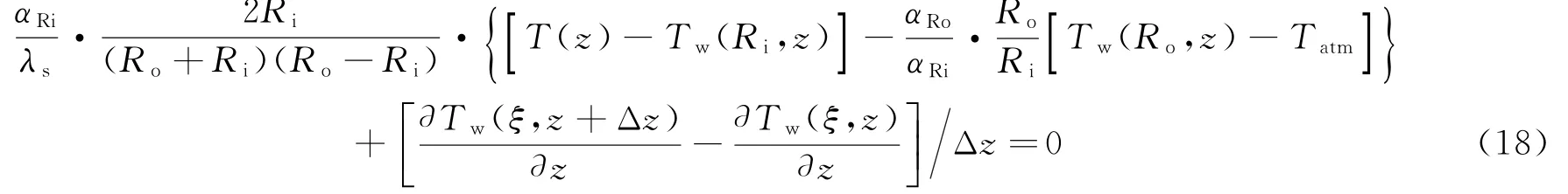
其中,ξ是筒体内径和外径之间的一点,其轴向温度梯度等于筒体横截面上轴向温度梯度平均值.

在筒体高温段,热量从壳侧流体传向筒体,一部分在筒体内沿轴向传递,一部分传递给环境.这时,式(18)中的第一项为正,即筒体轴向温度梯度的变化率为负,又由于筒体入口端面温度梯度为0,故在筒体内部,轴向温度梯度数值加速上升.由于筒体出口端面温度梯度也为0,故在筒体低温段,轴向温度梯度数值加速下降.筒体中心部分,由于轴向导热总是倾向于减小轴向温度梯度,故温度梯度的变化速率较小,与不考虑轴向导热时相比,筒体中心温度变化显得比较“平坦”.

由式(5a),筒体传热对管外流体的影响可用筒体传热与换热管外壁传热的比值γ表示,即

由式(19)可知:筒体导热系数与换热管导热系数之比越大、换热管外径与筒体直径之比越大、筒体内壁面对流传热系数与换热管外壁对流传热系数之比越大、筒体内壁面温度与管外流体主体温度的温差与换热管外壁面温度与管外流体主体温度的温差之比越大,筒体传热影响越大.

由上述对圆筒轴向导热的分析可知:从流体高温段、沿筒体长度方向,筒体内壁面温度先是低于但逐渐接近管外流体主体温度,而后交叉,高于管外流体主体温度且温差逐渐增大;在筒体进、出口端,筒体轴向导热影响最大;在筒体中间,轴向导热影响可以忽略不计.

在石化工程中,换热器筒体导热总体影响不到总传热负荷的1%.

筒体轴向导热会改变筒体内部及内、外表面温度,因而对筒体的平均金属壁温的计算有影响.从宏观传热上讲,筒体内轴向导热会将管外流体的热量从高温段传给低温段,造成管外流体热量的“短路”,并且导致局部和总体传热温差均减小,对传热不利.

3 数值求解与算例

上述内容仅是对换热管和筒体轴向导热的影响因素和影响大小做定性的分析,要得到准确的计算结果,需对上述控制微分方程和边界条件进行求解.当然,解析求解是非常困难的,本文采用有限差分方法进行数值计算法求解.

在圆柱坐标下对筒体和换热管进行均匀网格划分(见图2),控制容积的界面设在相邻节点的中心,将筒体和换热管内部微分方程离散为网格节点温度方程;运用向前或向后差分格式的边界节点离散控制微分方程,得到式(1)和式(2)的差分方程一般形式.

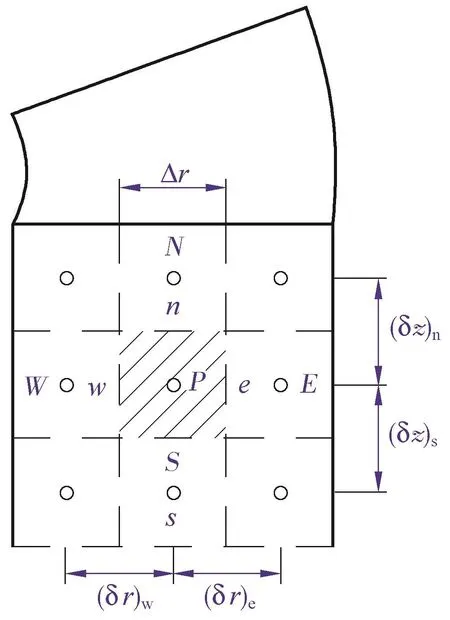
图2 圆柱轴对称网格系统

AP,AE,AW,AN,AS和aP,aE,aW,aN,aS是筒体和换热管离散方程对应的系数.其具体表达式可参考文献【12】.

边界条件对应的式(5a)和式(6a)的差分方程一般形式分别用式(2 1a)和式(2 1 b)表示,即

式中:

式中:

式(20a)、式(20b)、式(21a)和式(21b)中,I和J表示在某个维度上划分的点数,点数从1开始,一直到第I或J个点;点1、点I或点J分别在研究区域的两个边界面上;点i和j表示区域内部相应维度上的任意一个点..

表1是某高温快速撤热换热器的数据.下面以表1所给条件为例,考察轴向导热的影响程度.

表1 计算用数据表

由式(16)可得,该换热器换热管轴向导热的影响因子η约等于2．2.可见本例的换热管轴向导热影响明显,必须考虑.

本文对差分方程式(20a)、(20b)、(21a)和(21b)进行联立,反复迭代求解,直至收敛并达到满意的精度.为加快迭代速度,交替从冷、热流体入口温度开始,逐行扫描.

根据上述差分方程和计算方法,编制计算程序并计算.

4 计算结果与分析

表2为不同工况下的换热负荷和有效传热温差.

表2 不同工况下的换热负荷和有效传热温差

使用HTRI计算得到的换热负荷为10．86 k W,而使用数值模拟计算,不考虑换热管、筒体轴向导热时换热负荷为10．91 k W,相对误差0．46%,可见数据模拟结果令人满意.在考虑换热管和筒体轴向导热后,换热负荷和有效传热温差都下降了25．0%.可见对于类似本例的情况,换热管和筒体轴向导热不宜忽略,否则会导致较大误差.

图3显示了换热管轴向导热对管内流体和管内表面温度的影响.由图3可以看出:在考虑换热管轴向导热时,管内流体出口温度上升约190℃;管内表面温度梯度变小,显得更“平坦”.这是由于热流体高温段热量通过换热管壁轴向导热传递给了低温段的冷流体,造成热量从高温段到低温段的“漏流”,并导致局部传热温差减小、热流体出口温度上升.本例的计算结果显示,换热管轴向导热对传热的不利影响十分明显.

图3 换热管轴向导热对管内流体和管内表面温度影响

图4 显示了换热管和筒体轴向导热对管外流体、管外表面和筒体内表面温度的影响.由图4可以看出:在考虑换热管和筒体轴向导热时,管外流体出口温度下降约193℃;筒体内表面温度梯度变小,显得更“平坦”,并且在高温段低于管外流体温度,在低温段高于管外流体温度.筒体轴向导热会改变筒体内部及内、外表面温度,因而对筒体的平均金属壁温的计算有影响.在换热管和筒体轴向导热的“双重”作用下,管内热流体高温段热量通过换热管轴向导热、管外冷流体高温段热量通过筒体轴向导热,一起传递给了管外低温段冷流体,造成热量的“短路”,并导致局部和总体传热温差均减小,对传热不利.

图4 换热管和筒体轴向导热对管外流体、管外表面和筒体内表面温度影响

由于换热管和筒体两端绝热,换热管和筒体温度的轴向二阶导数(见图5)代表轴向导热对传热的影响.由图5可以看出:在冷、热流体高温段,换热管和筒体轴向温度二阶导数数值非常大,分别为6 466．63℃/m2(换热管内表面)、3 465．76℃/m2(换热管外表面)和1 070．96℃/m2(筒体内表面),说明换热管和筒体内部轴向热传导影响非常明显;符号为负,代表换热管和筒体内部部分径向传热转向轴向导热;在冷、热流体低温段,换热管和筒体轴向温度二阶导数数值非常大,分别为13 980．57℃/m2(换热管内表面)、13 980．57 ℃/m2(换 热 管 外 表面)和15 043．31℃/m2(筒体内表面),说明换热管和筒体内部轴向热传导影响非常明显;符号为正,代表换热管和筒体内部轴向导热转向径向传热;在离开换热管和筒体两端之后,换热管和筒体轴向温度二阶导数数值迅速减小,小于50℃/m2.可见轴向导热影响区域主要集中在换热管和筒体两端,离开换热管和筒体两端0．2 m之外的区域,轴向热传导可以忽略不计.

图5 换热管内、外表面和筒体内表面温度二阶导数

将换热管和筒体各点壁温加权平均,得到换热管和筒体平均金属壁温,与GB/T 151—2014计算结果进行对比,结果见表3.

表3 不同方法换热管和筒体平均壁温计算结果

从表3可以看出:有轴向传热的换热管和筒体金属壁温大大高于无轴向传热的计算结果,与GB/T 151的计算结果比较接近;有轴向传热的换热管和筒体金属壁温差比无轴向传热减少20．2%,无轴向传热的计算结果与GB/T 151的计算值非常接近.可见在本例中,轴向传热对换热管和筒体平均壁温及两者壁温差影响显著.

需要说明是,GB/T 151与数值模拟在计算换热管和换热器壳程筒体壁温时方法不同,主要表现在:GB/T 151使用冷、热流体进、出口温度的加权平均值和热阻分配方法;而数值模拟采用网格法逐点计算壁温后取平均值.因此两者计算结果相差较大.

GB/T 151方法不考虑轴向传热,计算方法简单,而且在本例中计算结果最保守,在工程设计上采用GB/T 151方法似乎更稳妥.但也并非一定如此.仍以本例为例,当考虑换热器与环境的热损失时,如果筒体内壁结垢、筒体内壁对流传热系数低以及筒体外部保温不良时,筒体金属壁温会显著降低,这就会加大管、壳程金属壁温差,导致其超过GB/T 151的计算结果,要特别注意.

5 结论

本文通过理论分析和数值计算,分析了轴向导热对换热管和筒体金属壁温的影响因素、影响大小和影响范围,得到以下结果:

1)通过理论分析,得到了换热管管内轴向温度梯度与径向温度梯度的公式、换热管和筒体轴向导热对主体传热影响大小的公式,可用以判断是否要考虑轴向传热的影响;

2)轴向导热会改变换热管和筒体金属壁温,并引起换热管和筒体的“热漏流”,对传热不利;

3)轴向导热影响范围主要集中在换热管和筒体的进、出口端部,在主体范围内,轴向导热的影响可以忽略;

4)筒体轴向导热与环境的热损失对筒体平均温度影响很大.在筒体内壁结垢、筒体内壁对流传热系数低以及筒体外部保温不良时,更要特别注意;

5)一般情况下,轴向导热可以忽略不计.但在一些特殊情况下,如高温、高真空、管内和管外流体流量很低、管长短但管内和管外物流温度变化很大、管壁和筒壁较厚且导热系数较高等条件下,应考虑轴向导热的影响.

符号说明:

Tw(R,z),tw(r,z)——分别为筒体壁和换热管壁温度,℃;

R,r——分别为筒体和换热管径向坐标,m;

z——为筒体和换热管轴向坐标,m;

L——筒体和换热管长度,m;

Ro,Ri——分别为筒体外、内半径,m;

ro,ri——分别为换热管外、内半径,m;

T(z),t(z)——分别为换热管外、内流体在轴向z处的主体温度,℃;

αRi,αro,αri——分别为筒体内壁、换热管外壁和换热管内壁流体对流换热系数,W