基于内状态变量理论的盐渍土本构模型研究

陈会官 朱珍德 王 震

(1.河海大学岩土力学与堤坝工程教育部重点实验室,南京 210098；2.河海大学 江苏省岩土工程技术工程研究中心,南京 210098)

冻结盐渍土广泛分布于我国西部高原地带,随着“一带一路”倡议的推进,该区域内的工程建设正迅速发展.冻结盐渍土是由土颗粒、未冻水、冰、气体和盐分组成的多孔介质,其物理与力学特性受冻结温度、盐含量、未冻水含量及所受压力的影响[1].

研究多种因素对冻结盐渍土的综合影响及推导相应的本构模型对该区域内工程设计、施工具有重要的指导意义[2].众多学者通过试验研究了不同含盐量、含水率、围压等因素对盐渍土冻结温度[3]、水盐迁移规律[4-5]、冻胀机理[6]、力学特性[7-8]等的影响[9].盐分的存在会减弱土体的水分迁移现象,从而影响冻结过程中的水盐迁移规律,最终导致土体内部未冻水含量的差异[10].不同围压下盐渍土的强度特征不同,从而影响土体的体积变形与剪切变形机制[11].然而,大多数试验仅考虑单一因素,鲜有考虑含盐量、含水率、围压对冻结盐渍土力学特性的综合影响.高娟,赖远明,常丹,等[11]建立了一个考虑加载速率影响的冻结含盐砂土强度准则.吕晶晶[12]以修正剑桥模型为基础,推导了一个冻结盐渍土的单屈服面本构模型.多数学者认为单一屈服面难以描述土体的变形特性,主张采用两个或多个屈服面[13].Lai Y 等[14]基于能量耗散理论提出一个冻结盐渍土的双屈服面本构模型,以预测不同盐浓度对土体力学特性的影响.但目前尚未有考虑冻结盐渍土内部未冻水含量与围压对土体力学行为综合影响的双屈服面本构模型.

鉴于此,基于内状态变量理论[15],提出一个考虑未冻水含量和围压综合影响的冻结盐渍土双屈服面本构模型.将未冻水含量与围压作为本征变量修正内状态变量理论.依据耦合了未冻水含量与围压的Helmholtz自由能,考虑土体的体积变形机制及剪切变形机制,建立一个增量型的双屈服面本构模型,并给出了详细的数值计算流程.最后对模型进行验证,在2.5%盐含量不同围压下模型模拟的轴向应力-偏应力曲线与试验结果吻合良好.

1 双屈服面本构模型

1.1 考虑未冻水含量和围压的内状态变量理论

冻结土体中未冻含水率可由公式(1)计算[1]

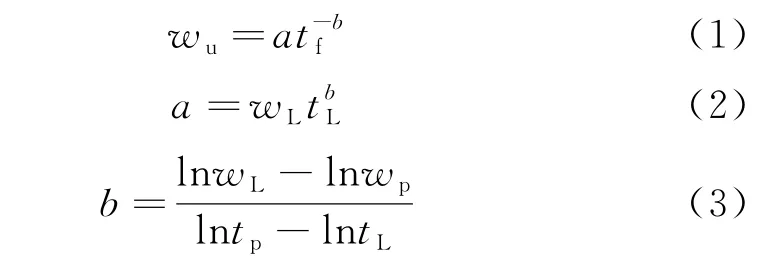
式中,wu为未冻水含水率(%)；wp为塑限(%)；wL为液限(%)；tf为冻结温度绝对值(℃)；tp为塑限 时的冻结温度绝对值(℃)；tL为液限时的冻结温度绝对值(℃).

在内状态变量理论中[16],本征变量为一些可以直接或间接观测的状态变量,一般为εe,T.在冻结盐渍土中,未冻水含量能够反映冻融对土体影响的程度,且可通过已有的公式进行计算.围压能够直接观测,且会对土体的变形特性产生影响.因此,可以将围压与未冻水含量作为本征变量对内状态变量理论进行修正,修正后的自由能可表示为：

式中,φ为单位质量的 Helmholtz自由能,vα为第α个内状态变量,与塑性应变有关vα=vα(εp),(α=1,2,…).

1.2 应变分解

考虑土体体积变形和剪切变形特性,采用两个屈服面来描述冻结盐渍土的变形行为.相应于球应变有一个压缩屈服面,相应于偏应变有一个剪切屈服面.双屈服面理论认为,随着加载方向的不同,土体可能只产生塑性体积应变或只产生塑性剪切应变,或两者同时产生,应变可分解为[17]：

弹性阶段应力增量与应变增量的关系可表示为[17]：

式中,K为体积模量；G为剪切模量.

依据能量分解原理：

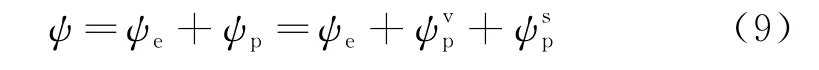
1.3 体积塑性变形

在土体体积变形过程中,相应的自由能可表示为：

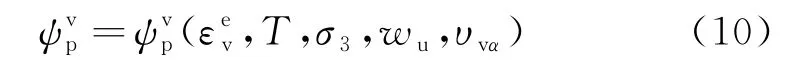
在内状态变量理论中,热力学力Avα与内状态变量vα相对应,共同描述材料内部的非弹性耗散.可表示为[18]：

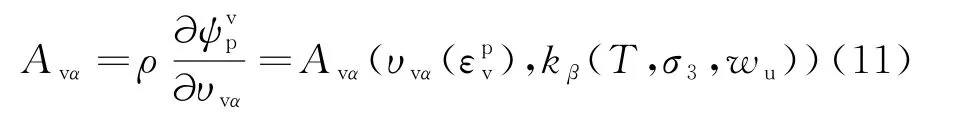
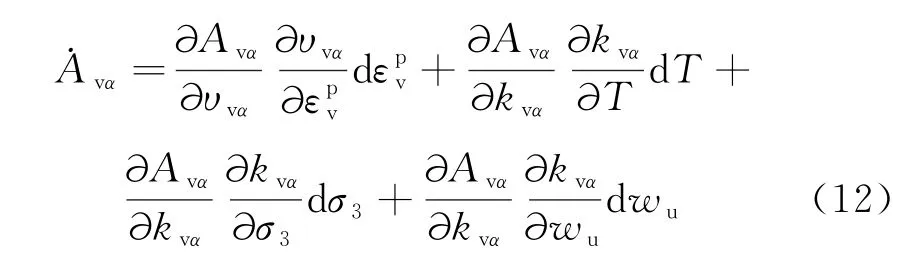
式中,kβ为反映材料内部耗散的耗散参数,与材料的特性与热力学力的选取有关.可表示为温度、围压、未冻水含量的函数,即kβ=kβ(T,σ3,wu).

体积变形屈服面方程,在应力平面p-q中表示为：

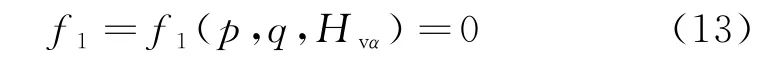
式中,Hvα(α=1,2,3,…)是表征体积塑性变形引起物质微观结构变化的参量,称为硬化参量,与体积塑性应变、温度和水分迁移量有关.则相应的势函数为[17]：

在经典损伤力学中[19],损伤常被看作损伤热力学力来探究材料内部损伤的演变.在塑性力学中,硬化参量Hvα可看作热力学力Avα来描述材料的非弹性变形,即：

不同的塑性变形机制所对应的应变可表示为：

相应的一致性条件可表示为：

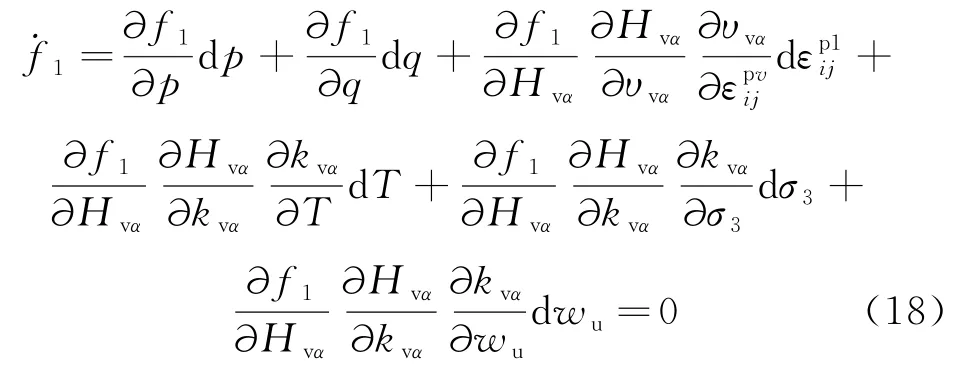
将公式(18)代入公式(17)可得：

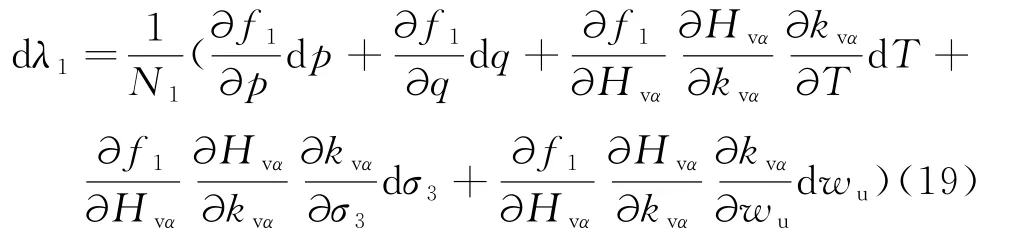
其中：

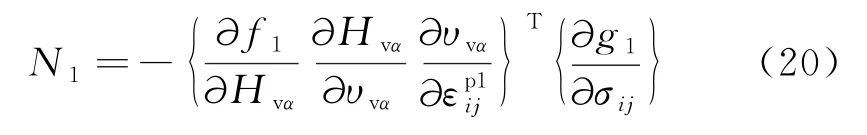
则体积变形机制下的塑性变形可表示为：

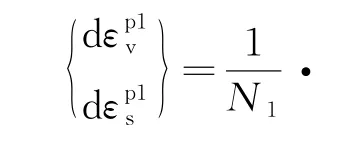
1.4 剪切塑性变形

依据修正的内状态变量理论,推导剪切机制下的本构与推导体积变形机制下的本构相似.自由能可表示为：

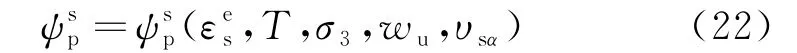
体积变形屈服面方程及势函数在应力平面p-q中可表示为：

则耦合了温度和水分迁移量的剪切塑性本构方程可表示为：

式中：

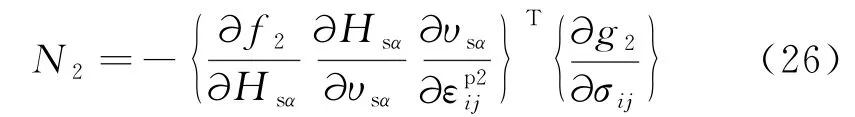
1.5 弹塑性本构方程

综合考虑土体的体积变形与剪切变形,土体的弹塑性本构方程可表示为：

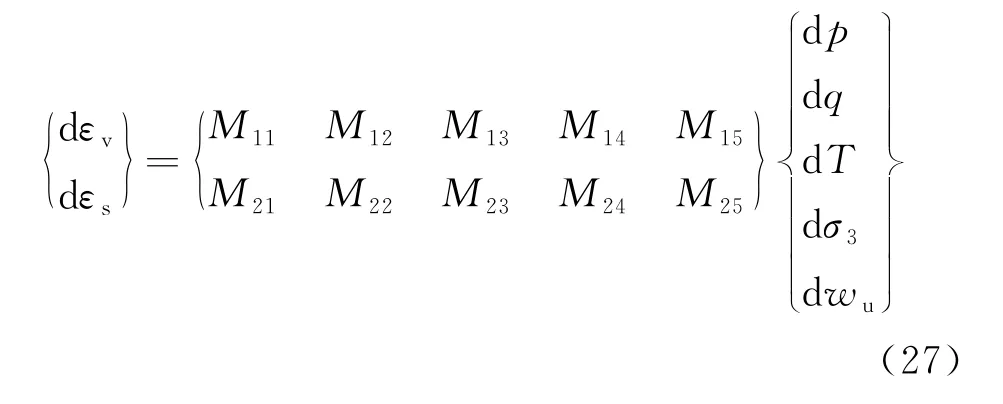
为考虑未冻水含量与围压综合影响的冻结盐渍土双屈服面弹塑性本构方程,式中Mij(i=1,2；j=1,…,5)为综合考虑公式(7),(8),(21),(25)的值.

1.6 数值计算流程

1)输入基本参数：盐含量S,温度增量ΔT,围压增量Δσ3,未冻水含量增量Δwu,轴向应力增量Δσ1；并输入第(n-1)步的过程变量值：σ1(n-1),T(n-1),σ3(n-1),wu(n-1)-1)

2)计算模型中耗散参数涉及的参数值及第n步的p(n-1),q(n-1),σ1(n-1),σ3(n-1),wu(n-1).

5)如果f1(p,q)＞0,依据公式(21)计算应变,否则

6)如果f2(p,q,)＞0,依据公式(25)计算应变,否则

图1 不同围压下的轴向应变-偏应变曲线[14]

2 模型验证

2.1 试验方案

2.2 屈服面选取

公式(27)为弹塑性本构模型的广义形式,屈服面、势函数的具体形式未给出,硬化参数及耗散参数的函数未明确.在实际应用中,应根据土体特性及工程条件选择恰当的屈服面、势函数、硬化参数及耗散参数表达式,从而推导出公式(27)的具体表达式.考虑冻结盐渍土的特性,体积变形屈服函数在修正剑桥模型基础上调整得到,剪切变形屈服面为考虑旋转硬化参数的抛物线函数[14].屈服面及相应的势函数取为[14]：

式中,p*为平均有效应力,为p的函数；α为屈服面的旋转角度,为的函数为硬化参数,为的函数；M0为初始应力比,描述三轴应力加载下的初始应力比；为参数值；θ为旋转硬化参数,为的函数；Cl为临界状态曲线在p-q平面上的截距[14].

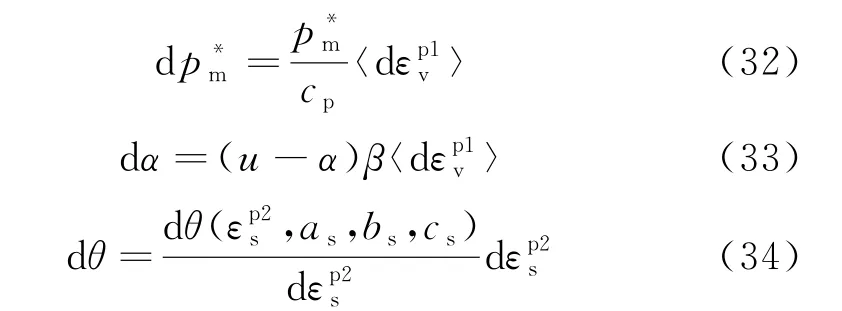
与第一节中的本构模型相对应,此处：

式中,耗散参数cp,u,β,as,bs,cs均为温度,围压,未冻水含量的函数.

2.3 参数识别

由于冻结过程中温度变化规律相同,且压缩过程均在-6℃下进行,因此可不考虑温度影响.试验中参数均在2.5%盐含量,不同围压下测得,因此仅需考虑围压对模型中各参数的影响.依据试验条件,与体积变形机制相关的耗散参数cp,u,β与围压为二次函数关系,可通过拟合得到各参数表达式；与剪切机制相关的耗散参数as,bs,cs与围压为三次函数关系,可通过拟合得到各参数的表达式.

2.4 结果对比

将各耗散参数表达式,硬化参数函数,及相应的屈服函数和势函数代入本构方程中可得到具体的Mij的值.依据1.6节的数值计算流程,将得到的本构方程(27)采用 Matlab 软件编程可得到盐浓度2.5%时不同围压下的应力应变曲线.

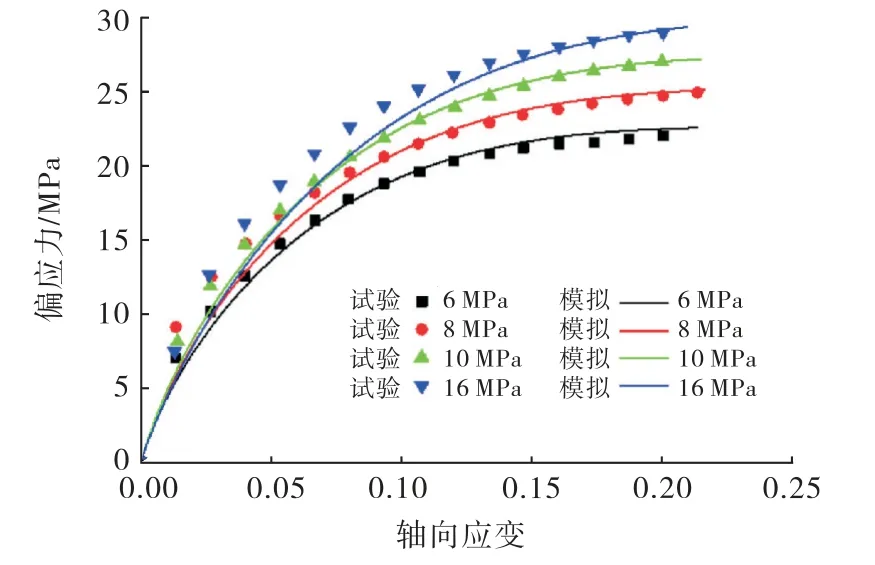
图2 模型模拟与试验结果对比

由图2可知,该模型能够准确地模拟不同围压下冻结盐渍土的轴向应变-偏应力曲线.通过定义恰当的热力学力及耗散参数,该模型能够很好地反映冻结盐渍土的力学行为.

3 结 论

依据修正的内状态变量理论,充分考虑围压和未冻水含量,本文在热力学框架下构建了冻结盐渍土的双屈服面弹塑性本构模型,并采用2.5%盐含量不同围压下的试验对模型进行验证,验证结果表明模型模拟结果与试验结果吻合良好.

1)本构方程(27)以广义形式给出,可以选取恰当的热力学势和耗散参数对模型进行具体化,以满足不同土体类型、盐类型和计算精度的需求.

2)该模型以增量形式给出,相较于全量模型,更适用于复杂应力历史条件下的计算.且给出了详细的数值计算流程,有利于模型的二次开发.

3)模型在热力学框架下推导,采用能够直接观测或计算得到的变量作为本征变量修正内状态变量理论,拓展了内状态变量理论的使用范围,为复杂条件下土体本构模型的构建提供了新思路.