基于爆破损伤的露天矿边坡稳定性的灾变分析

周子涵 陈忠辉 刘昱廷

(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083；2.三峡大学 土木与建筑学院,湖北 宜昌443002)

突变理论是法国数学家Thom[1]于1972年在前人基础上创立的,用来研究不连续现象,特别适用于描述作用力或动力的渐变导致状态突变的现象.由于边坡的失稳恰恰是一种由渐变至突变的自然现象,系统的真实特性与突变理论的思想很接近,均强调系统的非线性、不可逆性及动态的过程,并且特别适用于内部作用尚属未知系统的研究[2].因此,利用突变理论来分析边坡的失稳规律是行之有效的.

目前,突变理论已经在边坡稳定性的分析方面得到了广泛地应用,取得了丰硕的成果.龙辉,秦四清,万志清[3]等考虑滑面介质的应变软化和水致弱化性质,针对降雨触发的滑坡,通过突变理论分析发现了滑坡演化的过程,并在整体上深化了对斜坡失稳机理的认识.刘军,秦四清,张倬元[4]等利用弹性力学理论并综合考虑地下水因素建立了缓倾角层状岩体滑坡的尖点突变模型,通过对形成机制的分析,发现地下水是岩体突发失稳的一种触发因素,并提出了防治意见.秦四清[5]采用Weibull分布描述应变软化介质的剪应力与应变关系,运用尖点突变理论给出了滑坡失稳的充要力学判据.ZHU Hongwei[6]等在考虑了凝聚力、内摩擦角等因素的情况下,建立了基于突变级数法的图时边坡地震稳定性评价模型.QIANG Pei[7]等利用意大利的Ca,di Malta以及白鹤岭滑坡的监测数据,通过建立椭圆突变模型进行分析,确定出了岩质边坡的初始不稳定点和滑坡失稳的判据.

爆破震动及地下水作用是影响露天矿局部台阶边坡稳定性的两个重要外界因素.迄今为止,国内外学者利用突变理论对地下水作用下边坡失稳规律的研究已经屡见不鲜,而对于爆破震动因素的考虑仍然较少.因此,本文将在前人研究成果的基础上,引入爆破荷载因素,通过建立爆破荷载及地下水共同作用下的二维斜坡失稳力学模型,并考虑爆破震动对滑动趋势面介质的损伤弱化效应,对边坡在爆破震动影响下的失稳规律进行探讨,提出一种新的滑坡失稳判据,为预防露天矿边坡的岩体动力失稳提供理论支持.

1 突变模型的建立

1.1 力学模型

爆破震动和地下水作用是影响露天矿局部边坡稳定性的重要外界影响因素,而地下水作用又主要包含作用在边坡后缘裂隙的静水压力和作用在滑动趋势面上的扬压力等.因此,本文建立了如图1所示的二维斜坡滑动失稳力学模型.

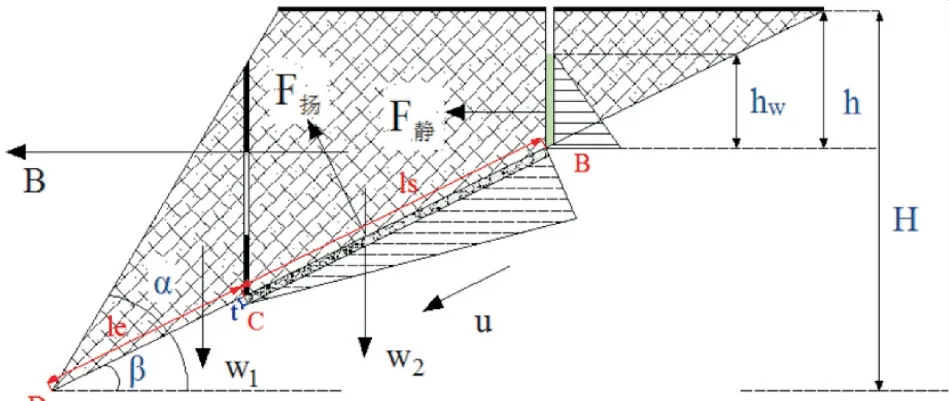
图1 斜坡滑动失稳力学模型

从图1中可以看出,滑动趋势面由3 个部分组成：第1个部分AB段为边坡的后缘张拉裂隙段,垂直深度为h,内部充有裂隙水,高度为hw；第2个部分BC段受爆破震动的影响较为强烈,层面岩体在爆破作用影响下通常以层裂的形式产生松动弱化,从而造成岩体力学参数大大降低,这里将该区段称为弱化层裂区段,长度为ls,该区段趋势面介质具有应变弱化的性质,初始内摩擦角为φ1,初始黏聚力为c1；第3个部分CD段,趋势面介质强度较高,粘结力强,与弱化层裂区段相比受爆破震动的影响较小,具有弹性或应变硬化的性质,这里称之为硬质结构面区段,该区段长度为le,趋势面介质内摩擦角为φ0,黏聚力为c0.边坡上部滑体为刚体,岩体重度为r,密度为ρ,边坡坡角为α,高度为H.硬质结构面区段范围内边坡滑体的自重为W1,弱化层裂区段范围内边坡滑体的自重为W2,滑动趋势面BD段的倾角为β,厚度为t,上部滑体在自重和外力作用下沿滑动趋势面产生的下滑位移为u.

由图1中的平面几何关系可以得到硬质结构面区段范围内边坡滑体自重W1和弱化层裂区段范围内边坡滑体自重W2分别为：

根据达朗贝尔原理可将爆破动荷载折算成等效静荷载,引入到边坡稳定性的计算.目前,常采用下述经验公式反映爆破震动的影响[8]：

式中：B为爆破震动作用力,方向水平指向采场,作用于潜在滑体的几何中心；m为上部滑体的质量；f为爆破震动主频率；βF为静力系数,一般取0.2～0.3；Q为一次实际爆破药量；R为测点与爆源的距离；K为与岩性、地质条件、爆破方法等有关的系数,称为相关系数；ξ为衰减指数,K和ξ可通过对现场实测爆破震动数据进行回归分析获得.

另外,当边坡后缘张拉裂缝中充水后,如果内部裂隙水得不到及时扩散,便会形成高压水流,产生很高的静水压力,给边坡造成一个明显的扰动,同时高压水流会沿着边坡的后缘裂隙渗入到固有的软弱潜滑面中,产生很高的浮托力,使边坡的抗滑力大幅度减小,极大地危害着边坡的稳定性[9].所以,本文在建模时考虑了地下水以上两种水力效应的影响,即后缘张拉裂隙中存在的静水压力和作用在弱化层裂区段上的扬压力,可分别表示为：

式中：F静为裂隙水静压力,水平作用在滑体上,呈三角形分布；F扬为作用在弱化层裂区段上的扬压力,呈三角形分布,方向垂直于斜面向上,亦称浮托力；其它符号的含义同前.

由于弱化层裂段趋势面介质易受爆破震动作用的影响,该区段介质岩体在周边爆破开挖的影响下,内部微裂纹会不断地延伸扩展,从开始的细观裂纹逐步发展成为贯通的宏观裂纹,使得该区段介质的松裂程度加剧,与硬质结构面区段介质相比,其力学参数所产生的损伤劣化较为严重,从而使得该区段介质的强度和力学参数大大降低.根据文献[10-11]所述,假定岩体为各向同性体,根据各向同性损伤理论,考虑爆破震动影响下的损伤劣化效应,弱化层裂段趋势面介质的抗剪强度参数及弹性模量可以近似采用下式计算：

式中：φ1x、c1x、Esx分别为受到爆破扰动影响,损伤劣化后的弱化层裂区段趋势面介质的抗剪强度参数和弹性模量；Φ1、c1、Es分别为弱化层裂区段趋势面介质的初始抗剪强度参数和初始弹性模量；Db为岩体爆破损伤变量,可根据下式计算求得[12]：

式中：Db为爆破损伤变量；Vi-1为第i-1次爆破后测试岩体的声波波速；Vi为第i次爆破后测试岩体的声波波速；ηi为第i次爆破后的岩体相对于爆前岩体的声波降低率.

至此,通过对图1中的斜坡失稳力学模型进行受力分析,可以得到边坡系统在自重及外力作用下的抗滑力和下滑力分别为：

式中：W为上部滑体的总重量,其中W=W1+W2；其它符号的含义同前.

考虑爆破震动作用的影响,弱化层裂段趋势面岩体损伤劣化后的剪切模量可表示为：

式中：Gsx为弱化层裂段趋势面岩体受到爆破震动影响损伤劣化后的剪切模量；νs为弱化层裂段趋势面岩体的泊松比,这里假定其是不变的,即不受外界因素的影响.

因此,根据式(12)可以对文献[13]中提出的弱化区段介质的本构关系进行修正,考虑爆破震动作用对弱化区段介质的损伤劣化效应,得到修正后的滑动趋势面弱化层裂段介质的本构关系为：式中：τ1为BC段介质的剪应力；Gs为未产生损伤劣化的BC段介质的初始剪切模量；u0为BC段介质本修正构关系曲线峰值点处对应的位移.根据式(13),就可以得到BC段介质修正本构关系曲线拐点处对应的位移u1=2u0.

滑动趋势面硬质结构面区段介质的本构关系可表示为[13]：

式中：τ2为CD段介质的剪应力；Ge为CD段介质的剪切模量；τm为残余抗剪强度.

BC段和CD段介质的本构关系曲线如图2所示.

图2 滑动趋势面不同介质的本构关系曲线

1.2 尖点突变模型

通过对如图1所示的二维斜坡滑动力学模型进行分析可知,边坡系统的总势能函数由3个部分,即硬质结构面区段和弱化层裂区段岩体自身的应变势能、下滑力F在位移u方向上产生的滑动势能和抗滑力R在位移u方向上产生的耗散能共同组成,总势能函数为：

根据突变理论的方法,选择滑动位移u作为状态变量,对式(15)中的总势函数V进行求导,得边到坡稳定性分析的平衡曲面为：

式(16)为力的平衡条件,再对总势能函数V进行3次求导,并根据V‴=0可得：

所以平衡曲面尖点处的剪切位移u=u1=2u0,与BC段介质本构关系曲线拐点处对应的位移值相同.

式(16)相对于尖点处状态变量值u1进行Taylor展开,取前3项,得到平衡曲面为：

对式(18)做变量代换,并将平衡曲面方程以尖点突变理论的标准形式进行表示有：

式中：x为无量纲状态变量；b、c为无量纲控制变量；λ为滑动趋势面中CD段岩体介质刚度和BC段受爆破震动作用影响的损伤劣化岩体介质本构关系曲线拐点处的刚度之比,这里简称修正刚度比；θ为与上部滑体重量、爆破作用力大小、后缘裂隙水高度、滑动趋势面抗剪强度等有关的参数,称为系统的几何力学参数.

根据文献[14],尖点突变理论模型分叉集方程的标准形式为：

将式(21)和式(22)代入式(25)中可得：

根据分叉集Δ和控制变量b的变化情况来分析岩质边坡在爆破荷载和地下水作用共同影响下的稳定情况.当Δ＜0时,系统发生突变,边坡产生失稳滑动；当Δ=0时,系统处于临界状态,边坡处于临滑状态,如果此时控制变量产生微小的变化,必然会引起平衡状态的改变；当Δ＞0时,系统稳定,边坡不会产生滑动[4].

综上所述,分叉集Δ＜0是边坡发生失稳的充要力学条件,而为了满足该充要条件,显然只有当Δ≤0时,才能成立,即只有在b≤0条件下才能跨越分叉点集.继而由式(21)和式(23)可以得到边坡在多种外力因素作用下发生滑动失稳的必要条件为：

由式(26)和分叉集的性质可得：

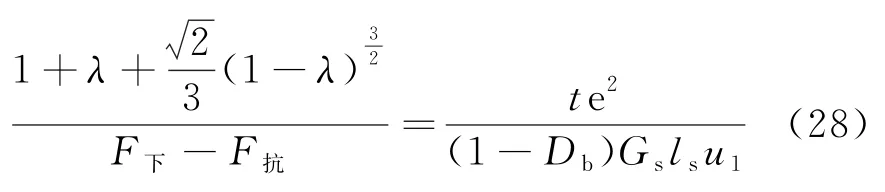
式中：F下和F抗分别为边坡的下滑力和抗滑力,具体形式参见式(10)及式(11).

根据刚性极限平衡理论,边坡的稳定性安全系数可表示为对应于位移u时的抗滑内力与外部作用所产生的合力的比值,即：

将式(28)代入式(29)有：

由式(29)和式(30)可知,边坡稳定性系数K与滑体重量、滑动趋势面修正刚度比、硬质结构面区段和弱化层裂区段的长度等多种内外影响因素均有关.由式(19)及式(25)可知,边坡在处于临滑状态时,其失稳临界点处的位移为[9]：

由式(30)和(31)可得：

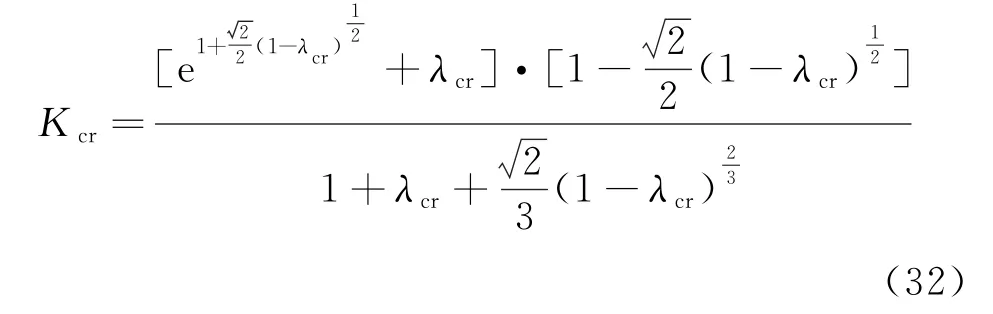
式中：Kcr称为边坡临界安全系数.

当边坡的安全系数K＜Kcr时,会发生失稳破坏；当K=Kcr时,边坡处于临滑状态；当K＞Kcr时,边坡不会发生失稳,可以看出,Kcr的大小可以反映边坡的稳定情况,Kcr越大,边坡发生失稳的可能性越大；λcr为边坡处于临界滑动状态时,CD段岩体介质刚度和BC段损伤劣化岩体介质本构关系曲线拐点处的刚度之比,简称临界修正刚度比.

2 滑坡失稳判据分析

由上述分析可知,爆破震动作用是露天矿局部边坡稳定性的重要外界因素,因此,可根据边坡在一定条件下所能够承受的最大临界爆破作用力提出滑坡失稳的判据.通过对方程(28)进行等式变换,可以得到边坡在一定条件下所能够承受的最大临界爆破作用力,即Bcr为：

根据式(3)及式(34)可以得到边坡在一定条件下所能够承受的最大临界爆破药量Qcr为：

从式(33)和(34)可以看出,边坡在发生失稳时所能够承受的最大爆破药量与滑体的质量,后缘裂隙的深度以及其内裂隙水的高度、爆源距离等因素均有关,并不是由单一的某因素决定的,即临界爆破药量的大小并不是固定不变的.

至此,可根据修正刚度比λ和临界爆破药量Qcr提出岩质边坡在爆破荷载、后缘裂隙水静压及滑动趋势面扬压力共同作用下发生失稳的判据条件：在满足边坡失稳必要条件λ≤1时,当Q＞Qcr时,边坡会发生失稳破坏；当Q=Qcr时,边坡处于临滑状态；当Q＜Qcr时,边坡处于稳定状态,不会发生失稳.如果不满足边坡失稳必要条件,即λ≥1时,边坡亦不会发生失稳破坏.

在露天矿的实际爆破开挖过程中,为了保证临近台阶边坡的稳定,防止爆破震动引起邻近台阶的局部滑动失稳,造成严重的后果,可应用现场声波测试对边坡潜在滑动面处岩体的爆破损伤及累积进度进行监测.通过获得每次爆破作业后潜在滑动面处岩体的波速降低率,利用式(6)～(8)近似地计算出受爆破震动影响损伤劣化后的趋势面介质的力学参数,并通过式(33)和(34)计算出在下一次爆破开挖时边坡能够承受的最大临界爆破药量,对后面的爆破开挖设计中实际药量的选择起到一定的指导意义.

3 算例分析

鞍千矿业有限公司许东沟采场长为1 740 m、宽为280～490 m.根据设计院一期开采设计,边坡采用靠帮两并段的开采方案.台阶高度为12m,部分并段高度24 m,采场东帮台阶坡面角为65°,采场西帮台阶坡面角55°.由于地下水以及爆破开采的共同作用,采场内边坡已有多处发生局部破坏.本文选择矿区内位于西帮的一处滑坡为例,将滑动面简化成如图5所示的滑动失稳力学模型.

铁矿爆区的爆破设计采用的是逐孔起爆技术,采用的起爆器材主要是采用高精度高强度的导爆管雷管,在地表主要采用的是25 ms导爆管雷管,孔内为400 ms的段别,采用的炸药种类主要是乳化油炸药,爆破的相关参数见表1.

表1 爆破相关参数

研究边坡位于采场西帮,并已经出现了局部的变形破坏现象(如图3所示),边坡与爆源的相对位置平面图以及边坡滑动的二维简化力学模型分别如图4和图5所示.经现场勘探及室内外试验的测定,该区域岩体类型主要为磁铁石英岩,自坡顶向下一定深度处存在局部贯通的泥岩夹层,相关参数见表2.

表2 实测边坡参数

图3 现场滑坡现象

图4 边坡与爆源的相对位置平面图

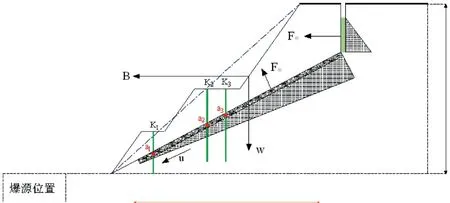
图5 边坡的二维简化模型

该处边坡在滑坡前,在其相邻台阶处进行过多次爆破作业,获得的爆破震动相关数据见表3.

表3 4次爆破的相关数据

如图5所示,K1、K2、K3分别为选取的边坡在失稳前的部分声波测试孔的布置位置,分别位于由下至上的两个台阶上,孔深分别为15 m、20 m、20 m.通过对3个测孔处的岩体进行爆破前后的声波测试,得到3 个测试孔内的边坡泥化夹层处附近位置,即a1、a2、a3三个位置处的爆破前后声波测试结果见表4.

表4 声波测试结果

经计算,该处边坡在4次爆破后的临界修正刚度比分别为λcr1=0.74、λcr2=0.87、λcr3=0.94、λcr4=0.98,均满足失稳的必要条件.将上述临界刚度比分别代入式(32)可以得到边坡临界安全系数随爆破次数的变化曲线,如图6所示.由图6可以看出该处边坡的临界安全系数随爆破次数的增加而呈现递增的趋势,边坡失稳的可能性在不断提高,同时也说明了边坡失稳滑动的发生通常不是由某一次爆破作业造成的,而是由于多次爆破的累积作用所致.

图6 K cr 随爆破次数的变化曲线

通过计算,各次爆破前边坡所能够承受的最大临界爆破药量和各次爆破的实际药量对比如图7所示.

图7 临界药量与实际药量的对比

由图7可以看出,前3次爆破的实际药量均小于相应的临界药量,而第4次爆破的实际药量大于其临界药量,根据前面提出的滑坡判据条件,由于Q＞Qcr,第4次爆破边坡会发生失稳,与实际情况相符,验证了判据的合理适用性.

4 结 论

本文基于如图1所示的二维斜坡平面滑动失稳力学模型,引入爆破荷载因素,运用尖点突变理论研究了爆破荷载和地下水共同作用对露天矿岩质边坡稳定性的影响,结论如下：

1)在满足边坡失稳必要条件,即修正刚度比λ≤1时,当Q＞Qcr时,边坡将发生失稳破坏；当Q=Qcr时,边坡处于临滑状态；当Q＜Qcr时,边坡处于稳定状态.如果不满足边坡失稳必要条件,即λ≥1时,边坡不会发生失稳.

2)边坡失稳的可能性随爆破次数的增加而不断提高,同时也说明了边坡失稳滑动的发生通常不是由某一次爆破作业造成的,而是由于多次爆破的累积作用所致.

3)通过将4次爆破作业的临界药量和实际药量进行对比,验证了利用导出的滑坡失稳判据评价边坡的稳定情况是合理可行的.