RBF神经网络与遗传算法的离心泵优化设计

杜梦星 王彦伟 张相志

(武汉工程大学 机电工程学院,武汉 430205)

离心泵作为流体机械,广泛地应用于化工、石油及农业等各个领域,对国民经济的发展起着不可小觑的作用.在离心泵各个组件中,叶轮作为离心泵最重要的部件之一,其外型的设计直接影响到离心泵的各项性能,因此想要设计出优越的离心泵,对叶轮的优化设计是关键点.在传统的离心泵优化设计中主要采取经验公式用于映射离心泵各项性能与影响因素之间的关系,然后在考虑约束的情况下用数值最优计算方法求得目标函数的最优值[1].这种方式虽然因简捷易行而应用较广,但却由于叶轮的性能与变量间是复杂的非线性关系而往往难以得到恰当的函数模型,使得传统的优化算法在优化叶轮的应用上受到限制.近年来,随着CFD 技术与优化算法的不断发展,许多对叶轮性能优化的研究都采用将流场分析与优化算法相结合的方式,通过构造性能参数的优化目标代理模型而获取最优值[2].

随着智能优化设计被广泛应用于各行各业,人工神经网络由于具有很强的非线性映射能力和不需要任何假设而被运用到离心泵的性能预测及优化,目前很多学者都采用BP(back-propagation)神经网络结合优化算法对关系函数进行寻优[3].BP 神经网络具有学习精度高的优点,但学习速度较慢且收敛性差.为了克服算法自身特性,本文采取学习速度快且逼近能力强的径向基函数(radial basis functio-n,RBF)神经网络来实现对离心泵代理模型的构建,利用遗传算法(genetic algorithms,GA)求解优化模型,获取最优解,以期为离心泵叶轮的优化设计提供参考.

1 数值模拟

1.1 叶轮几何结构参数

选取型号为Q25H52单级单吸卧式离心泵为研究模型泵,设计工况下流量Q=25 m3/h,设计扬程H=52 m,设计转速n=6 600 r/min.叶轮进口直径D0=44 mm,叶片入口直径D1=40 mm,叶轮外径D2=100 mm,叶片出口宽度b2=8 mm,叶片包角φ=110°,叶片流道中线入口安放角β1=25°,叶片出口安放角β2=30°,叶片数z=6,离心泵叶轮几何参数如图1所示.

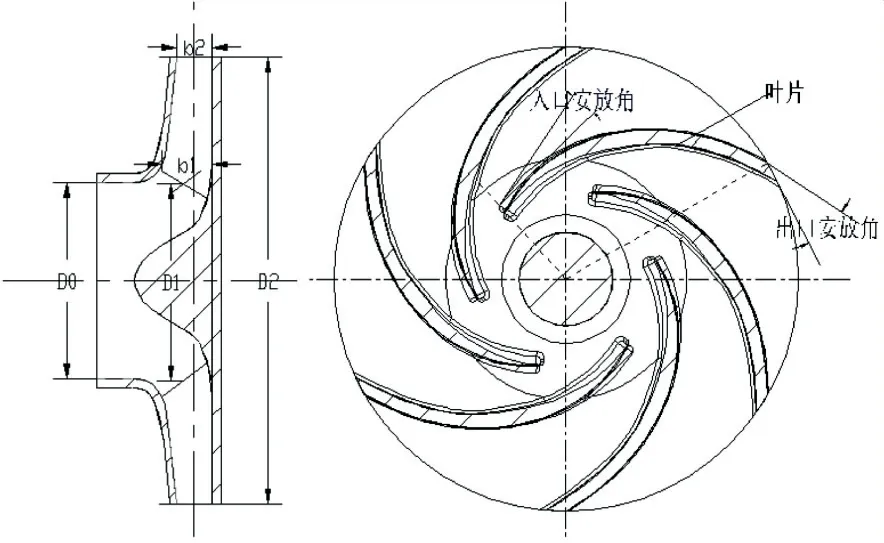
图1 离心泵叶轮几何参数图

1.2 水力计算单元划分

计算网格单元是CFD 模型的几何表达形式,也是模拟与分析的载体,网格质量的好坏直接影响到CFD 计算精度和计算效率[4],高质量的网格不仅能够保证计算结果的准确性[5],而且后续样本的流场优化分析更加顺利.为了实现对离心泵进行高质量的网格划分,应该考虑到在近壁区域网格分布有足够的网格节点[6].本文采用Pro/E 建立离心泵蜗壳、叶轮及叶片的三维模型,并构造出流道模型,利用ANSYS ICEM 对计算域网格划分,由于泵结构复杂,采用非结构网格进行划分,得到的离心泵水力计算域的网格划分如图2所示.此外,为了确保网格对计算精度不造成影响并节约计算时间,对网格进行了无关性分析[7],如图3所示.在进行网格划分时通过改变平滑度及相关中心粗糙度,分析6种不同单元数量网格独立性,当网格数量从30万左右增加到160万左右时,泵扬程的计算结果是相似的,因此,选择网格大约有186万个节点的方案.

图2 网格无关性分析

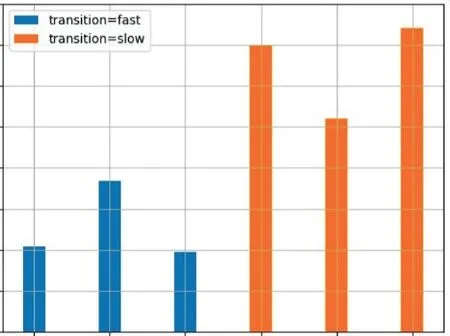
图3 计算域网格划分

1.3 仿真参数设置

为了实现优化前后离心泵叶轮性能的对比,对原始叶轮进行数值模拟计算.在对泵的边界条件设置上,进口采用压力边界条件,压力设置为1 atm,方向与叶轮轴线重合；出口根据工况流量采用流量出口边界条件,设置质量流量为6.94 kg/s；固壁边界为无滑移条件,边界条件设置完毕后如图4所示.

图4 计算域边界设置

在计算中,湍流模型为k-ε模型,采用三维不可压缩黏性流场,控制方程选用三维雷诺平均的N-S方程.在非定常数值模拟中,采用多重参考模型(MRF),假定网格单元做匀速运动,旋转部件与静止部件的交界面设置为Frozen Rotor,求解离散设置为二阶迎风格式,物理时间设置为叶轮转速的倒数1/ω,收敛残差设置为10-4.

2 优化设计

2.1 离心泵性能影响因素的确定

由于离心泵结构参数类型较多,其中有些参数只对特定的性能影响显著,而对其他性能参数不显著,以效率和扬程最优为优化目标,筛选出对扬程及效率影响显著的结构参数[8]：叶片进口安放角、叶轮前盖板圆弧半径、叶轮后盖板圆弧半径、叶片出口安放角、叶轮出口宽度及叶片包角.参考王春林,胡蓓蓓,冯一鸣,等的Plackeet-Burman 试验[9],对叶轮的上述性能参数进行试验设计,并由Design Expert完成结果分析.如表1所示为选取的主要性能参数及其对应的两组水平,水平值分别为参数值的0.8倍和1.2倍,试验采用N-12的设计,余留2个空白项用于估计误差.

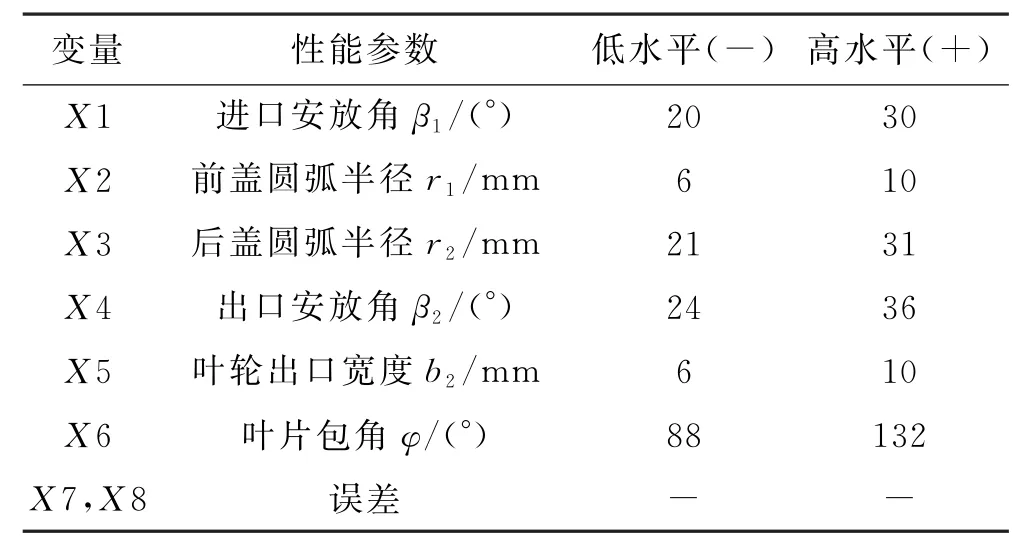
表1 Plackett-Burman试验高低水平设计表

利用Fluent下的ICEM CFD 软件获取12组相应最高效率的试验结果,并对其进行方差分析,结果见表2.可以看出模型的Prob＞F为0.045 4,小于0.05,说明此模型显著；决定系数R2=0.978 8,表明有97.88%的实验数据可用于模型回归方程的解释.

表2 方差分析结果

对各参数的分析结果见表3.

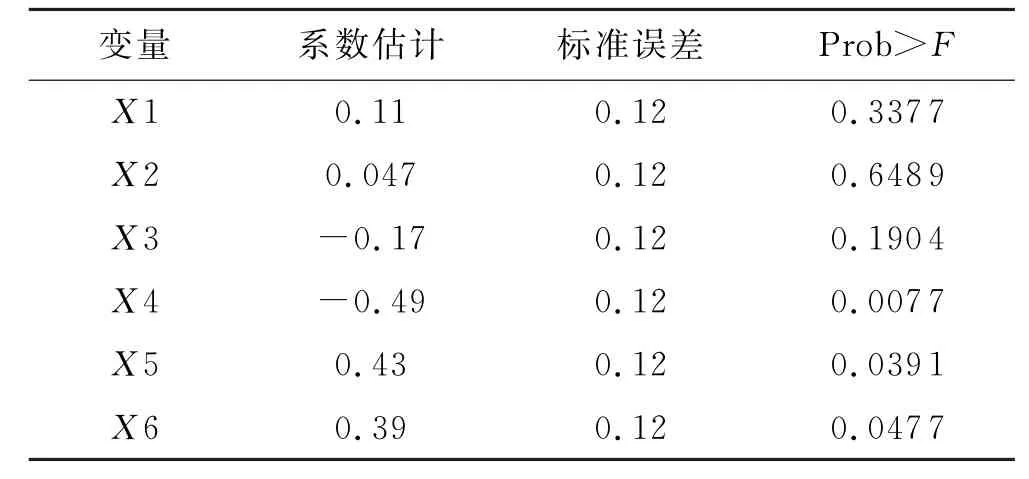
表3 性能参数显著性分析结果

其中叶轮出口宽度、叶片出口安放角以及叶片包角在95%的概率水平差异显著,因此确定以叶轮出口宽度、叶片出口安放角及叶片包角作为离心泵叶轮优化设计中的变量.

2.2 试验数据样本的建立

往期对利用神经网络对泵进行优化设计时所需要的试验设计样本数据大多以均匀设计获得.为了减少试验顺序对实验的影响,本文采取一种可以平衡试验顺序的拉丁超立方抽样方法(LHS).该方法解决了蒙卡抽样样本大、效率低等缺点,采用分层抽样的方式,在较低样本量的情况下,提升了抽样效率.

拉丁超立方设计(LHD)试验中把对试验目标有影响的变量称为因子,把因子的变化状态称为水平[10].其原理是在n维变量设计空间中,将每一个维度的变量区间进行m等分,随机选取m+1个样本点以保证每个因子的各个水平被研究且仅被研究一次[11].本文研究扭曲叶片叶轮出口宽度b2、叶片出口安放角β2 及叶片包角φ3种因子对离心泵扬程及效率的影响,b2的取值范围为6～15 mm,β2 的取值范围为25°～40°,φ的取值范围为100°～140°,每个因子取30个水平,图5所示为随机拉丁超立方设计生产的样本点分布.

图5 随机拉丁超立方设计试验

上述取30个水平符合神经网络训练样本数量至少满足输入层变量数的10倍原则,取随机生成的样本数据点并进行数值模拟.表4为部分试验数据和计算结果,其中出口宽度、出口安放角及叶片包角为通过拉丁超立方设计试验在取值范围内生成的性能参数值,将每个样本点进行数值仿真计算,得到所对应的泵的效率及扬程,用于后续神经网络的构建.

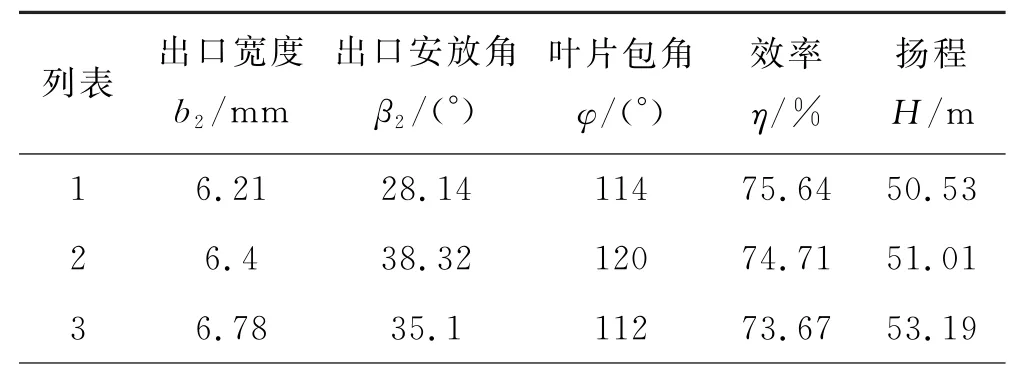
表4 部分试验数据及数值模拟结果

续表4 部分试验数据及数值模拟结果

2.3 RBF神经网络模型的建立

RBF是由MOODY 和MARKEN 提出的一种神经网络[12].它是一种3层前馈状型的神经网络,其结构包含有输入层、隐藏层、输出层,从输入节点到隐藏层节点的变换是非线性的,而从隐藏层节点到输出节点的变换是线性的,因此能以任意精度逼任一连续函数,非常适用于非线性动态系统的建模.

本文将Matlab作为RBF神经网络的编写语言,设定隐藏层激活函数为高斯径向基函数radbas,输出层激活函数为线性函数purelin；根据选取性能影响因素设计网络的输入节点为3个,分别为叶片出口宽度、叶片出口安放角及叶片包角；输出节点根据优化设计目标设置为效率和扬程；对于隐藏层神经元节点个数设置最大为200,目标误差为10-4,迭代显示频率设置为1,迭代次数等同于样本个数.

根据上述网络参数,使用newrb函数建立BRF神经网络[13],将表1所示的数据样本用于训练BRF神经网络,其训练过程误差变化曲线如图6所示.从图中可以看出当迭代27次后,误差已经小于10-4,达到了误差精度要求.

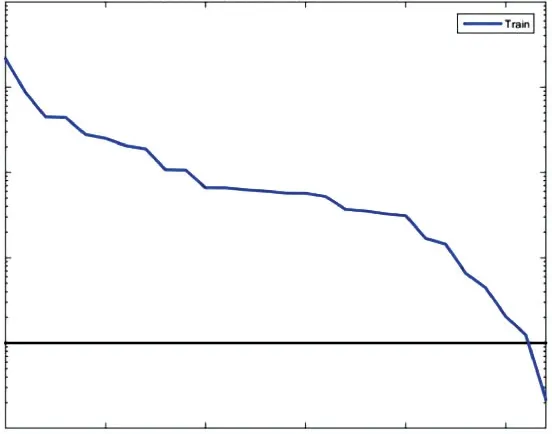
图6 RBF神经网络训练误差变化曲线图

将训练样本作为预测数据代入到RBF神经网络中,得到效率及扬程的预测值,如图7～8所示.分别为通过CFX 得到的效率及扬程数值计算值与通过BRF神经网络得到的效率及扬程预测值对比图,从图中可以看出数值计算值和预测值之间的误差较小.

图7 CFX 与RBF效率对比图

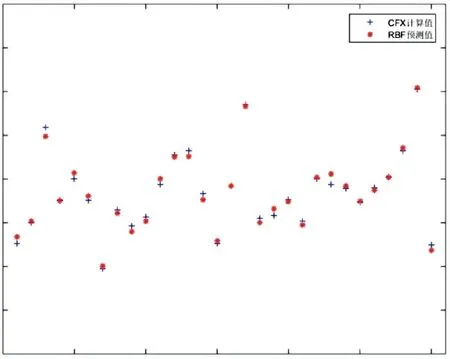
图8 CFX 与RBF扬程对比图

为了验证神经网络预测的可靠性,采用拉丁超立方设计随机生成5 组离心泵影响因素测试数据,见表5.

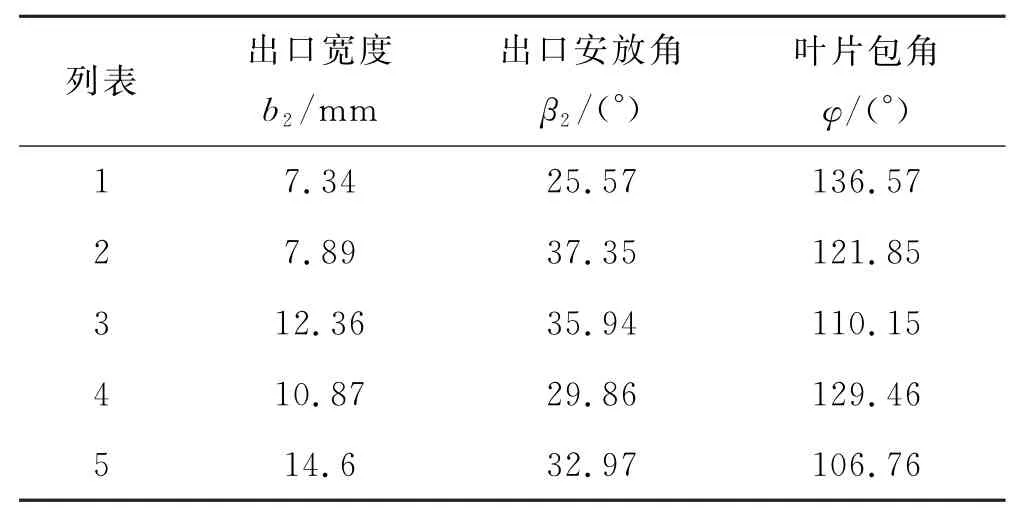
表5 随机生成的5组测试数据

将其作为测试数据利用神经网络进行效率和扬程预测,并将输出的结果与CFX 数值计算进行对比及误差分析.从表6、7中可以看出,效率最大误差为2.89%,扬程最大误差为1.4%,均在工程许可范围内.因此建立的BRF 神经网络所预测的效率及扬程可用于后续工作.

表6 CFX数值计算与BRF网络预测效率对比

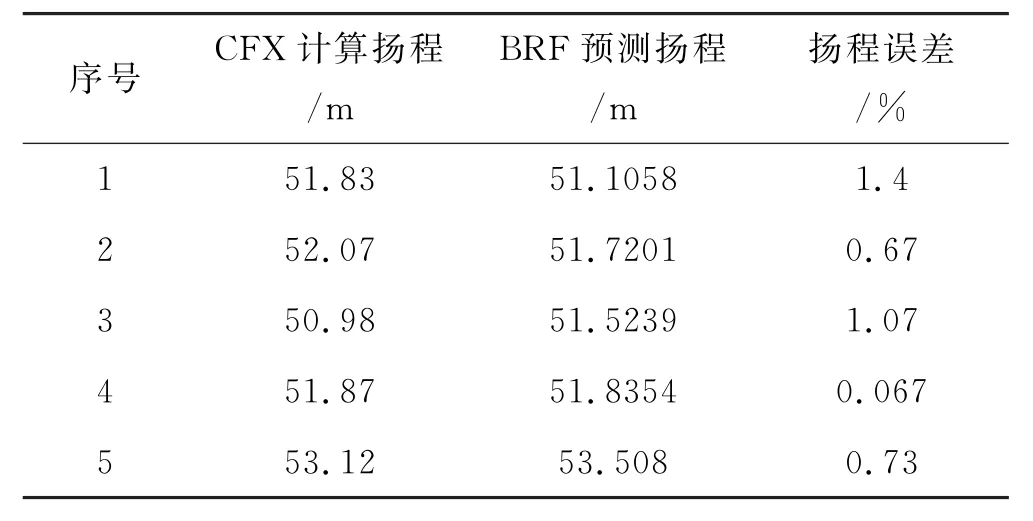
表7 CFX数值计算与BRF网络预测扬程对比

2.4 遗传算法全局寻优

遗传算法是由Holland提出的一种模拟生命进化机制的搜索与寻优的方法,它通过借鉴达尔文的物竞天择、适者生存的自然选择、遗传机理[14],实现能够求解问题并全局寻优.在利用遗传算法进行寻优时,将会从初始种群开始搜索,其中每一个个体都是染色体,其不断迭代的过程称为遗传,在遗传中用适应值来衡量后代的好坏,根据适应度进行部分保留和部分淘汰,经过若干代后既保持了种群大小不变又收敛于最好的染色体[15].

染色体对应着所求问题的可行解,每个染色体都由一组二进制字符组成.本文所用的二进制字符串有24位,图9所示为编码示意图,总分为3段,前8位表示叶轮出口宽度,中间8位表示叶轮出口安放角,后8位表示叶轮包角,二进制解码后代表其实际值.

图9 染色体二进制编码示意图

在利用遗传算法进行全局寻优时,以离心泵水利效率及扬程代表适应度,它们的大小代表该染色体的优劣,定义种群大小为100,最大遗传代数为50次,个体长度按上述二进制编码方式设置为8,代沟为0.95,交配概率为0.7,变异概率为0.01.

3 优化结果分析

3.1 遗传算法全局寻优

对优化目标与设计参数建立了RBF神经网络结合遗传算法的近似模型,如图10、11所示.图10为随着迭代次数的增加每一代中效率最大值的变化曲线,从图中可以看出,在迭代35次左右后算法收敛,泵效率趋于稳定,其值接近85%；图11为取最优效率及扬程的散点分布图,图中以横轴为扬程,以纵轴为效率,其中可以清楚地看到效率与扬程的分布情况,基本覆盖在影响因素设定取值范围内的效率与扬程点,并可与其对应得到叶轮的几何参数.

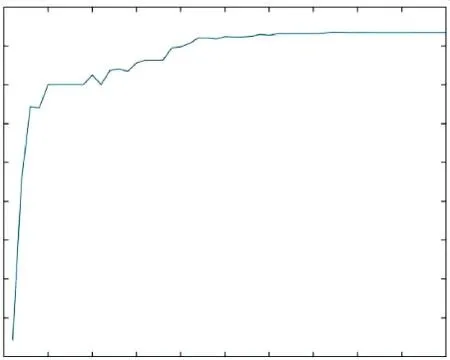
图10 最大效率随遗传代数变化曲线

图11 最优效率及扬程散点分布图

为研究优化后叶轮结构与性能变化,从散点分布中选取最优点对应的结构参数进行三维造型和数值模拟,并在设定同样工况下与初始个体进行比较分析.表8为优化前后离心泵叶轮影响参数和性能对比.可以看出,叶轮出口宽度和出口安放角减小,叶片包角增大；通过数值模拟得到设计工况下的效率为74.87%,扬程为54.21 m,均比优化前有所提高.

表8 优化前后泵影响参数及性能对比

3.2 优化前后内流场对比

对优化前后离心泵水力计算域内流场分析,可以更加直观地分析泵的工作情况.图12为优化前后泵中心截面压力分布云图.可以看出,叶轮流道内的静压值从叶片入口到出口呈现出均匀上升的趋势,且在相同半径处叶片工作面的静压力要大于叶片背面的静压力,在叶轮的出口位置,由于受到蜗壳的影响,静压力明显变化；蜗壳流道内的静压力值从叶轮出口到蜗壳第八截面随着半径增大大致为均匀分布,当水流到达扩压管后,压力最大；对比分析优化前后压力云图,离心泵内部流动趋势非常相似,由于液体在进入叶轮后与叶片边缘发生碰撞,从而在叶轮进口处产生负压区域,相比于优化前,负压区域明显缩小.

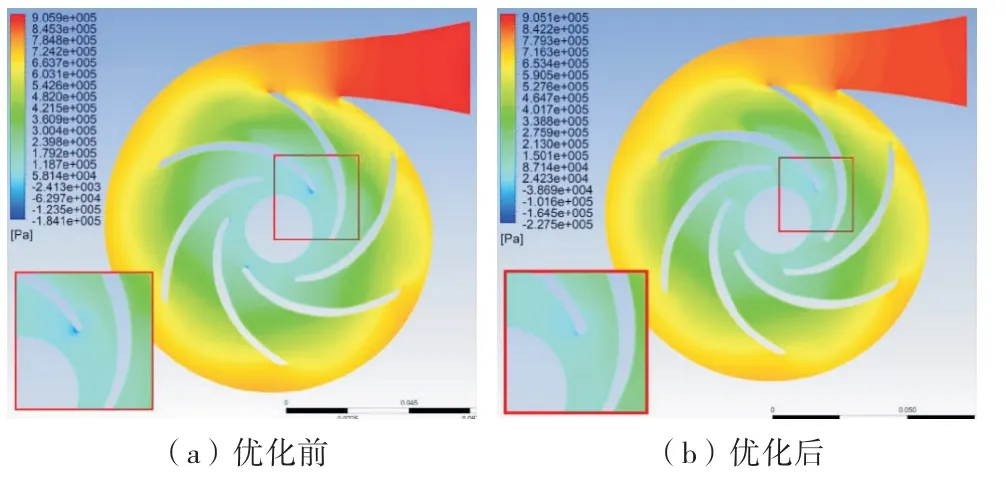
图12 优化前后泵流域静压力分布云图

图13为优化前后泵内相对速度分布云图.在蜗壳内部随着流道的扩大和叶轮水流入口的增加,蜗壳内的流速逐渐减小,当过了蜗壳第八截面后,随着流道的突然扩张再次变小；优化前叶轮在蜗壳流道最窄所对应的叶片流域中存在较明显的水流涡旋,这必然导致能量的损失,而优化后此区域涡旋减小,使得水流效率提高.

图13 优化前后泵流域相对速度分布云图

4 结 论

本文首先采用拉丁超立方试验设计方法对扭曲叶片叶轮离心泵的几何尺寸进行了30组方案设计,并采用CFX 数值模拟对设计数据进行了仿真,得到对应的效率及扬程；其次以其为训练样本,带入到BRF神经网络进行训练,得到了能够较准确预测效率和扬程的近似模型；最后,采用遗传算法结合BRF神经网络对影响因素设定的取值范围内进行全局选优,得到了叶轮的最优几何参数并进行了数值模拟及仿真,对比了优化前后内流场情况,得到的结论如下：

1)根据离心泵性能影响因素分析,得到了叶轮出口宽度b2、叶片出口安放角β2 和叶片包角φ为对优化目标最为显著的影响因素,并采用拉丁超立方试验设计方法进行随机抽样,克服了在均匀性方面的不足,试验样本取值满足输入层10倍的原则,在较低样本量的情况下,提升了抽样效率.

2)根据拉丁超立方试验样本建立了BRF神经网络并得到了近似模拟,对其预测结果与CFX 数值模拟结果进行误差分析,得到效率最大误差为2.89%,扬程最大误差为1.4%,因此该模型预测结果可作为实际数值模拟结果.

3)采用遗传算法并以BRF神经网络为目标函数对研究模型进行优化,对设定叶轮几何参数范围内进行全局寻优,得到最优个体.对比优化前模型,分析表示叶轮出口宽度和出口安放角减小,叶片包角增大,效率提高了3.87%,扬程增加了2.21m,增幅达到了4.25%,提升了泵效率.