分子非晶体系中结构弛豫的非线性动力学研究
王利民,王冰涛,陈泽明, 田永君
(燕山大学 亚稳材料制备技术与科学国家重点实验室,河北 秦皇岛 066004)
0 引言
非晶材料一直被人类所关注,无论是生活中随处可见的硅酸盐玻璃、应用于航空航天等先进领域的非晶合金[1],还是各种电子元器件中广泛存在的非晶半导体,以及医药行业有着亮眼表现的非晶药物[2-3],均体现着非晶材料的各自特殊性能。但是,非晶材料还存在着一些重要的问题尚未解决。例如,非晶材料在热力学上处于非平衡态,有向平衡态和稳定态转变的趋势。如何预测和评估动力学行为,直接关系到非晶的稳定性问题。同时此问题的解决将极大促进对非晶物理的深入认识。本文以小分子非晶体系结构弛豫过程中的非线性特征为研究对象,分析了非线性动力学的基本特征与基本规律,以期探索出非线性特征与非晶材料其他两大结构弛豫动力学特征(非简单热激活和非指数性)间的关系,建立更加完善的结构弛豫动力学知识体系。
1 结构弛豫中的非线性特征
1.1 玻璃化转变
液体在降温至熔点以下时成为过冷液体,继续降温,若晶化能够避免,在某一温度下过冷液体转变为玻璃态,称之为玻璃化转变,该温度为玻璃转变温度。玻璃化转变过程中,体系的焓和体积等参量连续变化,并不会如同晶化时存在热力学突变,但其比热容以及热膨胀系数在玻璃转变温度附近发生突变。不仅如此,玻璃化转变过程与其热历史有关,严格来说并非可逆过程,一直以来,关于玻璃转变是否为热力学相变的问题是一个具有挑战性的话题。玻璃化转变温度Tg在动力学上,一般定义为粘度(η)达到1012Pa·s或弛豫时间(τ)达到100 s时所对应的温度[4];而在热力学上,一般是选取某一速率下升降温热容曲线上的热容发生跳跃时的温度进行表征[3,5]。
玻璃化转变的热历史不同会导致最终的玻璃性质不同,为表征玻璃的热力学状态,Tool于1946年提出结构温度Tf的概念,定义材料玻璃态所处的状态与平衡液态相同时的温度为结构温度[6]。因此,玻璃化转变将随温度降低的平衡液体的构型熵锁定在玻璃转变温度的结构温度Tf处[7]。
1.2 弛豫过程中的非线性特征
Lillie于1936年在对无机玻璃的粘度的研究中发现粘度的变化具有时间依赖性[8],即与热历史有一定关系,而对热历史的依赖性正是玻璃态弛豫动力学的典型特征,即非线性特征。这是非线性特征最早的发现。1955年Hara与Suetoshi通过温度跳跃实验,发现体积弛豫函数依赖于温度跳跃的方向,也就是与温度变化的热历史有着直接的关系,从而真正证实了弛豫过程中非线性特征的存在[9]。Kovacs在对polyvinyl acetate(PVAc)的体积弛豫研究中也证明了这一点,如图1所示[10]。
图1 PVAc不同温度的体积弛豫曲线
Fig.1 Volume relaxation curves of PVAc at different temperatures
玻璃弛豫过程中的非线性特征可以使用温度跳跃实验进行表征[11-12],如图2。第一种情况是将处于平衡态的体系快速降温,由T1骤降至T2,而后在T2恒温处理,此时性能随温度发生变化,逐渐达到一个新的平衡,如右图上面的曲线。第二种情况是将处于平衡态的体系由T3骤升至T2,而后在T2下恒温处理,则亦会发生相似的过程,由右图下面曲线所示,体系同样向新平衡态趋近,但其回复过程明显较降温时更慢。由此可见,玻璃态中某一温度下的等温弛豫动力学与玻璃的热历史密切相关,属于典型非线性行为。
为量化玻璃态弛豫动力学中由于结构的变化造成的影响,即非线性特征,在弛豫时间的温度函数中引入结构温度Tf变量以表征非晶的结构状态,并使用非线性因子x表达结构对弛豫性能改变的贡献量[13],定量给出了非晶弛豫动力学对热历史的依赖程度:
(1)
式中,τ0为前置因子;h为玻璃转变激活能;x为非线性参数,取值在0~1之间。当x为1时,表征体系弛豫过程为线性,其弛豫过程沿平衡态外延至低温,与热历史无关;x小于1,表征体系温度在Tg以下弛豫动力学为非线性,且取值越小,对热历史(即玻璃结构状态)的依赖越大。图3给出了一个例子。
图2 温度跳跃实验性能曲线和弛豫时间线
Fig.2 Temperature jump program and corresponding relaxation measurements
图3 不同非线性参数值下的结构弛豫时间对温度的依赖关系
Fig.3 Reciprocal temperature dependence of structural relaxation time with various nonlinear parameters
2 研究方法与手段
研究非晶态的非线性特征,一般采用差示扫描量热仪(Differential Scanning Calorimeter, DSC)得到样本的热容曲线,并通过拟合得到非线性因子。应用最多的是Tool-Narayanaswamy-Moynihan-Hodge(TNMH)方程,其先后由Tool[14-16]、Narayanaswamy[17-18]、Moynihan[6]以及Hodge[19-20]提出、补充与完善。该方程由两部分组成,一部分是对于非线性因子在弛豫时间函数上的引入,如式(1),另一部分是对Tf的求解,即

(2)
式中,β是非指数因子,q为冷却或加热速率,本实验中选为20 K/min。式中结构温度Tf的实验值可由Moynihan[7]提出的方法进行计算得到:
(3)
式中,Cp-normal为归一化热容,Cp-liquid为液体热容,Cp-glass为玻璃态热容。TNMH方程由于考虑到了非指数性因子在弛豫过程中的影响,其对包括非指数性、非线性在内的玻璃化转变相关动力学参数都可以给出理想的拟合值,并且拟合过程简便有效,是研究者们广泛使用的模型之一[21-28]。
当将退火时间作为主要变量[29-30],可利用TNMH方程的等价形式计算Tf,如式(4),该形式在处理等温退火的弛豫过程时,具有明显的优越性。
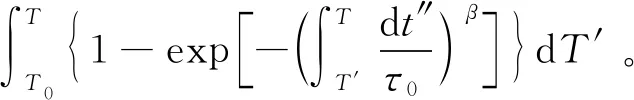
(4)
除TNMH方程之外,KAHR公式[31],Peak shift法[32]、Adam-Gibbs法等[33],均在非晶材料结构弛豫的研究中存在一定的应用。
3 纯物质玻璃形成体系的结构弛豫研究
小分子体系大多具有良好的玻璃形成能力,图4与图5给出了一个对药物扑热息痛分析的实例,实验采用标准先降温后升温方式,降温速率选用5、10、20、30、40 K/min,固定升温扫描速率为±20 K/min。图4是实验测量的不同冷速冷却到玻璃转变温度以下,再升温的玻璃转变Cp曲线。图5实线是利用式(3)对±20 K/min对应的Cp曲线计算得到的归一化热容曲线,虚线是利用式(1)和(2)得到的拟合曲线,据此可给出x=0.43和β=0.668。其中的激活能h既可从弛豫时间的温度关系中获得,也可基于冷却速率的Tf关系获得[4]。表1中引用了近些年受到关注的部分小分子玻璃形成体系的特征参量x和β,并以此做出非线性因子与非指数性因子[34]的分布图,如图6所示。可以观察到,非线性因子和非指数性因子具有同步变化的趋势,x随β的增加而增加。更重要的是,也观察到非线性因子普遍较非指数因子低。
图4 药物扑热息痛不同降温速率对应的升温热容曲线
Fig.4 Heating heat capacity curves of acetaminophen glasses quenched at different cooling rates
图5 药物扑热息痛归一化热容曲线和拟合曲线
Fig.5 Normalized heat capacity curve of acetaminophen glass and TNMH fitting
4 混合玻璃形成体系的结构弛豫研究
4.1 理想混合体系的特征参数研究
选取互为同分异构体的间甲基苯甲酸甲酯(MMT)与邻甲基苯甲酸甲酯(MOT)配成的二元混合溶液作为研究体系,两者由于结构极其相近,不仅完全互溶,且可以视为理想混合体系。以摩尔百分比配制74∶26、50∶50、25∶75三个比例的MMT与MOT的混合溶液,采用标准升降温速率(±20 K/min)扫描得到不同组分的升温热容曲线,如图7左图所示。之后对得到的曲线进行归一化处理和拟合,图7中右图为MMT含量XMMT从0到100%的归一化与拟合热容曲线。表2给出了不同组分下的特征参数。图8比较了这一体系非线性因子与非指数性因子随组分变化的情况。
表1 部分小分子玻璃材料的特征参数值
Tab.1 Characteristic parameters of some small molecule glass materials
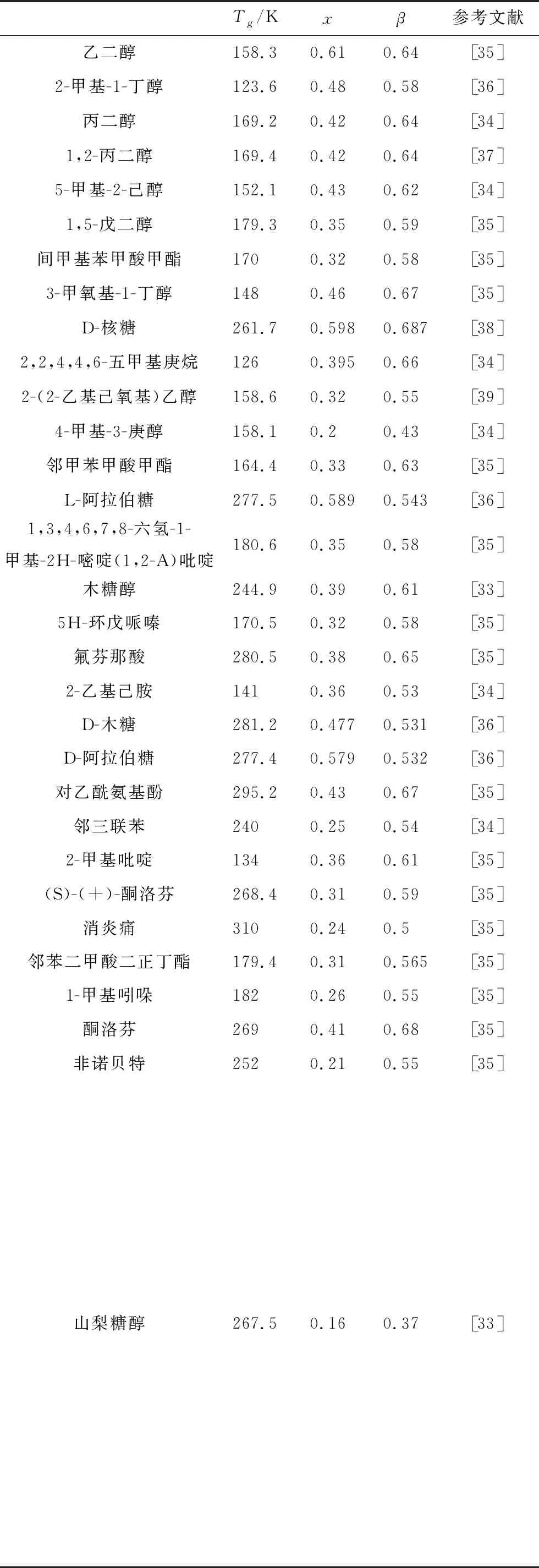
Tg/Kxβ参考文献乙二醇2-甲基-1-丁醇丙二醇1,2-丙二醇5-甲基-2-己醇1,5-戊二醇间甲基苯甲酸甲酯3-甲氧基-1-丁醇D-核糖2,2,4,4,6-五甲基庚烷2-(2-乙基己氧基)乙醇4-甲基-3-庚醇邻甲苯甲酸甲酯L-阿拉伯糖1,3,4,6,7,8-六氢-1-甲基-2H-嘧啶(1,2-A)吡啶木糖醇5H-环戊哌嗪氟芬那酸2-乙基己胺D-木糖D-阿拉伯糖对乙酰氨基酚邻三联苯2-甲基吡啶(S)-(+)-酮洛芬消炎痛邻苯二甲酸二正丁酯1-甲基吲哚酮洛芬非诺贝特山梨糖醇158.30.610.64[35]123.60.480.58[36]169.20.420.64[34]169.40.420.64[37]152.10.430.62[34]179.30.350.59[35]1700.320.58[35]1480.460.67[35]261.70.5980.687[38]1260.3950.66[34]158.60.320.55[39]158.10.20.43[34]164.40.330.63[35]277.50.5890.543[36]180.60.350.58[35]244.90.390.61[33]170.50.320.58[35]280.50.380.65[35]1410.360.53[34]281.20.4770.531[36]277.40.5790.532[36]295.20.430.67[35]2400.250.54[34]1340.360.61[35]268.40.310.59[35]3100.240.5[35]179.40.310.565[35]1820.260.55[35]2690.410.68[35]2520.210.55[35]267.50.160.37[33]
图6 小分子玻璃形成体系以及混合体系中不同物质非线性因子x与非指数因子β的关系
Fig.6 Relationship between the non-linear factorxand the non-exponential factorβin the small molecule glass forming systems
表2 MMT和MOT混合溶液的特征参数
Tab.2 Characteristic parameters of the glass transitions in MMT and MOT mixtures
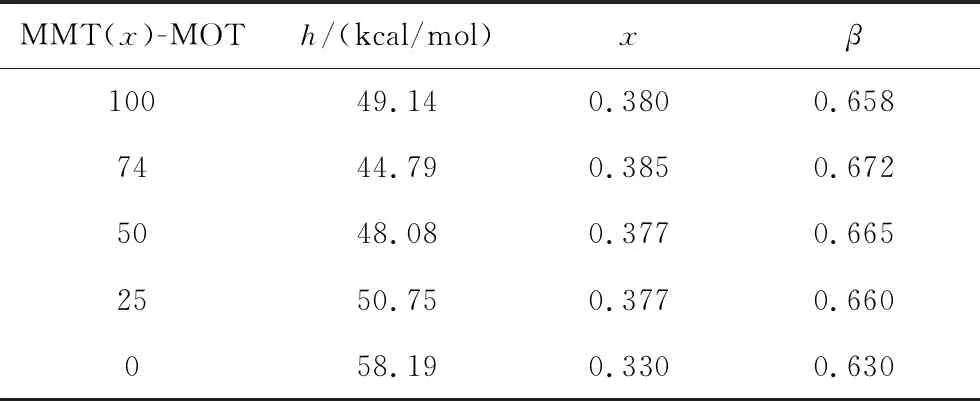
MMT(x)-MOTh/(kcal/mol)xβ10049.140.3800.6587444.790.3850.6725048.080.3770.6652550.750.3770.660058.190.3300.630
可以看到,非指数性因子和非线性因子随组分变化的偏离方向一致,均为正偏离。与纯物质相同的是,MMT-MOT混合体系中非线性因子的值均低略于非指数性因子。显然,在混合体系中非线性因子与非指数性因子同样也具有一定的密切关联。
4.2 非理想混合体系的特征参数研究
选取结构上有较大差别,混合热较大的1,2-丙二醇(PG)和2-乙基己胺(EHA)作为非理想混合体系的样本。以摩尔比配制了90∶10、68∶32、59∶41、42∶58、23∶77五种组分的混合溶液,保证混合溶液均匀性的前提下,开展了相关的测试研究工作。给出了混合体系不同组分下的升温热容曲线(如图9左图),同时对标准升降温速率(±20 K/min)下得到的升温热容曲线进行归一化处理,并采用TNMH方程对混合体系的归一化热容曲线进行拟合(如图9右图),图中自左到右为PG量从0到100%。将由归一化曲线计算得到的动力学特征参量列于表3,同时做x与β对组分的变化曲线,如图10。同时将得到的理想混合与非理想混合体系的x与β值也表示在图6中,即三角。
图7 MMT和MOT混合溶液的升温热容曲线(左)以及归一化热容曲线和拟合曲线(右)
Fig.7 Heating heat capacity curve of MMT and MOT mixtures (left) and normalized heat capacity curve as well as TNMH fitting curves (right)
图8 混合体系中非线性因子和非指数性因子随MMT摩尔百分数分变化的关系
Fig.8 Non-linear and non-exponential factors as a function of mole percentage of MMT component in the MMT-MOT mixtures
在图10中,排除了PG组分为23%时的异常点,可以看到,x与β的变化趋势大致相近,同时非指数性因子β均大于非线性因子x,同样符合纯物质以及理想混合体系中得到的规律。尽管在理想混合体系与非理想混合体系中,x或β随组分的偏离方向不同,但两种情况下,非线性参数与非指数性参数的偏离方向总是保持同步,且非线性因子均小于非指数性因子,说明二者的关联无论在纯物质中还是在混合体系中都是一致的。揭示这一普适关联对于理解和鉴别非晶体系中的非晶线性因子具有重要的应用价值。
图9 PG和EHA混合溶液的升温热容曲线(左)与归一化热容曲线和拟合曲线(右)
Fig.9 Heating heat capacity curves for the glass transitions in PG-EHA mixtures (left) and normalized heat capacity curvesas well as the TNMH fitting results(right)
图10 非理想混合体系中非指数性因子和非线性因子随PG组元摩尔百分数的变化关系
Fig.10 Non-exponential factors and non-linear factors as a function of mole percentage of PG component in PG-EHA mixtures
表3 PG和EHA混合溶液的特征参数
Tab.3 Characteristic parameters of the glass transitions in PG and EHA mixtures
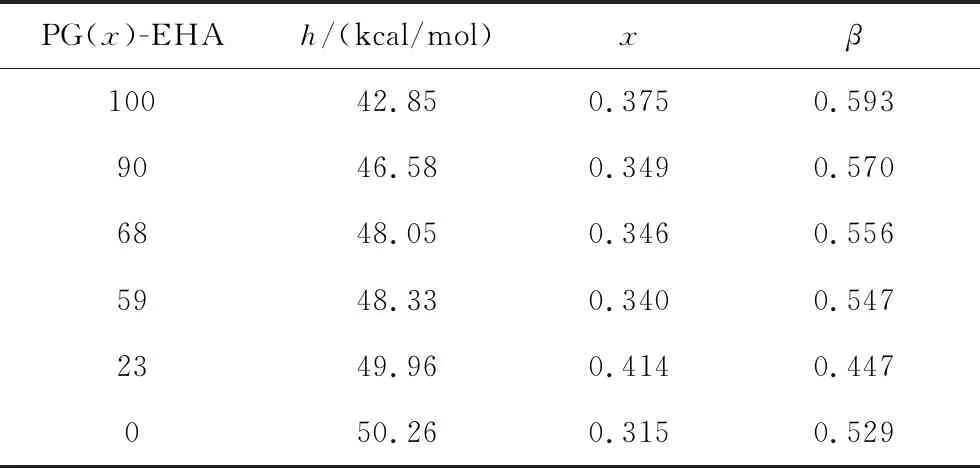
PG(x)-EHAh/(kcal/mol)xβ10042.850.3750.5939046.580.3490.5706848.050.3460.5565948.330.3400.5472349.960.4140.447050.260.3150.529
有关非线性因子随组分变化的相关研究较少,通常集中在某一组分下研究包括非线性参数在内的多个动力学参量的变化[40-41]。本文实验结果清楚表明不同混合模式的混合体系中,非线性参数随组分偏离的方向均和非指数性参数相同。Svoboda对(GeS2)y(Sb2S3)1-y玻璃的弛豫动力学进行了研究,对其数据随组分分析也同样发现非线性因子与非指数性因子变化趋势相近[42]。
5 三乙酰甘油酯的等温退火研究
5.1 不同退火时间下的非指数因子
选取结构简单,玻璃形成能力强的小分子三乙酰甘油酯进行研究,将样本分别于198 K温度下退火60、180和420 min后降至低温,之后再进行升温测量,得到热容曲线。之后对其进行归一化处理,归一化热容曲线和拟合曲线如图11所示。
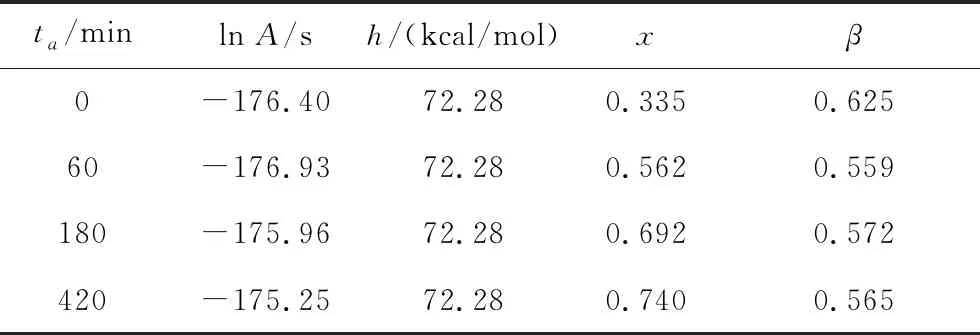
图11中除(a)以外,最下方的虚点线是未经退火的归一化热容曲线,用于对照。黑色实曲线代表样本经不同退火时间得到的归一化热容曲线,点划线是拟合时,保持激活能、非线性因子、非指数因子不变情况下,仅仅改变退火时间从而计算得出的结果。发现拟合曲线普遍与实验曲线严重不符。与黑色实线重合的间断线是调整非线性和非指数因子后的拟合曲线,发现利用该方法得到的β、x随退火时间ta的改变,发生非常大的变化,数据如表4。可以看到随着退火时间的增加x在数值上大幅变化,而且出现非线性因子高于非指数因子的情况,可见直接使用TNMH方程的一般形式对等温结构弛豫进行定量拟合分析会出现较大的误差。
图11 三乙酰甘油酯等温退火不同时间后的归一化热容曲线和对应的拟合曲线
Fig.11 Normalized heat capacity curve and corresponding TNMH fitting in the triacetinglasses subjected to isothermal annealing of at differdent time
表4 三乙酰甘油酯在198 K下等温不同时间后再升温曲线拟合参数值
Tab.4 Fitted parameters of reheating curves for triacetin after aging for different times at 198 K
ta/minln A/sh/(kcal/mol)xβ0-176.4072.280.3350.62560-176.9372.280.5620.559180-175.9672.280.6920.572420-175.2572.280.7400.565
5.2 不同拟合公式对拟合参数的影响
采用针对等温退火的TNMH方程的等价形式(式4)对三乙酰甘油酯在198 K下退火后的曲线进行拟合,得到了结构温度Tf与退火时间之间的拟合曲线,如图12。
图12中实线为采用TNMH方程等价形式拟合得到的结果,点代表实验数据,对比可以看出,拟合较为符合实验曲线。对比上文中TNMH方程原始升温形式在198 K下的拟合结果,等温退火TNMH方程的拟合结果更符合实际情况,因此升温TNMH方程的适用范围虽广,但在处理等温退火实验结果来获得玻璃弛豫参量时精度还有待提高,在 Svoboda[43]以GeTe4为样本对TNMH方程以及Adam-Gibbs方程的准确性对比中也证明了这一点。
图12 三乙酰甘油酯198 K下的结构温度与退火时间关系图及相应的拟合曲线
Fig.12 Structural temperature of triacetin as a function of annealing time at 198 K and the corresponding fitting curve
6 结束语
作为非晶结构弛豫的重要参量,非线性因子在弛豫动力学中占据了重要的地位。本文应用TNMH方程对小分子非晶体系的非线性参数进行了研究,观察到非线性因子与非指数因子具有密切关联,且非线性因子普遍低于非指数因子,这为基于非晶材料的非指数因子来评估和预测非线性因子提供了实验支撑。对应用TNMH方程的不同形式得到的拟合结果进行对比,发现在处理等温弛豫数据来确定非线性因子时应用等温TNMH方程更可靠。此外,非线性因子同非指数因子等动力学特征参量之间的关系还停留在定性阶段。同时对于非线性因子的有限研究,多是非指数性和非简单热激活两大特征研究过程中的附属品,因此开拓非线性因子研究的新途径、增添非线性因子研究的新手段亦是必要的。

