乘法分配律的教学设计与思考

鲍海林

[摘要]传统的教学中，教师引导学生寻找答案、方法和结论，只要学生死记硬背，把知识反复训练后“吞进肚子”即可，强调的是结果。在“乘法分配律”的教学中，教师创设了一个学生比较感兴趣的情景，引导学生自主参与知识形成的过程，让学生分几个小步骤来学习，既重视结果又重视过程，促使学生形成良好的数学情感和价值观。

[关键词]乘法分配律;巧设情景;逐步学习;灵活应用

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0058-02

【教学内容】人教版教材四年级下册第三单元第六课时“乘法分配律”

【教学目标】

1.在春播秋收活动中计算收获成果，了解乘法分配率的意义，并能应用乘法分配率解决相关问题。

2.通过听、看、画、摆、说，总结乘法分配率的公式。

3.在实际操作与活动中让学生感受数学知识的获得过程，激发学生学习数学的兴趣。

【教学重点】乘法分配率的理解与应用

【教学难点】乘法分配率的意义以及推导过程

【教学过程】

一、情景导入

师（演示课件）：体育课上，同学们在做春播秋收的游戏，需要在规定的时间内从起点出发到指定地点用篮子装玉米后拿回起点，拿的次数不限。每个玉米的质量为350克，拿得最多的为胜者。

二、问题探究

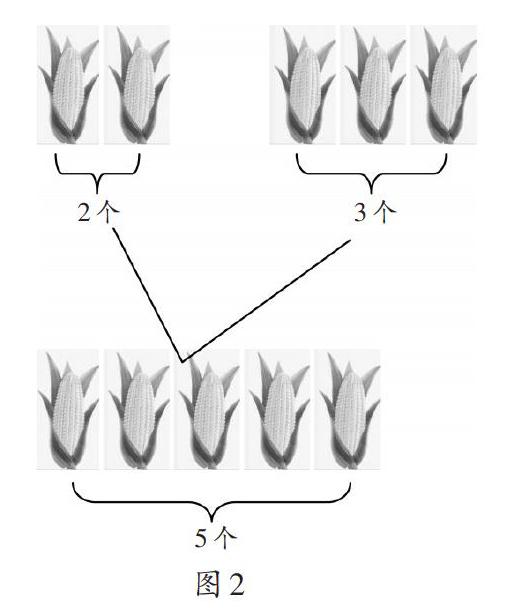
问题1：小明在规定时间内拿了2次，第一次拿了3个玉米，第二次拿了2个玉米。小明拿的玉米一共为多少克？

师：如何列算式？你是怎样想的？

（1）从总个数出发

分析图：（体现合的思想）对应算式：

①分步计算3+2=5（个），5x350=1750（克）。

②综合算式（3+2）x350=1750（克）。

（2）分次计算

（体现分的思想）

对应算式：3x350+2x350=1750（克）。

（3）对比算式

5x350=（3+2）x350=3x350+2x350。

师：你有什么发现？

【设计意图：学生分析图形后知道可以运用两种方法解题，初步理解两种方法的具体含义。】

问题2：小红在规定的时间也拿了2次，第一次拿了4个玉米，第二次拿了1个玉米。小红拿的玉米一共为多少克？

师：你能自己试着画一画，或者摆一摆，并能列出算式吗？

（学生先自主尝试，再在小组内交流，最后在班上交流）

生：5×350=（4+1）×350=4×350+1×350。

【设计意图：学生运用图形和学具进行演示、分析，学会应用两种方法解题，加深对算理的理解。】

问题3：如果小亮在规定时间内拿了2次，试问：小亮如果获胜需要拿多少个玉米，怎么拿？他拿的玉米一共为多少克？

分析：小明一共拿了5个，小红也拿了5个，小亮如果想获胜，则2次至少要拿6个才行。

算式：

（5+1）×350=5×350+1×350;

（4+2）×350=4×350+2×350;

（3+3）×350=3×350+3×350;

（2+4）×350=2×350+4×350;

（1+5）×350=1×350+5×350。

【设计意图：引导学生运用两种数学思想列式，从而通过算理理解算式并总结规律。】

三、规律归纳

师：分析以上解题过程和算式，归纳出乘法分配律的公式。

师：求一个数乘几个数的和，可以把这个数分别和这几个加数相乘，再把它们的积相加，结果不变，叫作乘法分配律。反之，求一个数与几个数的积的和，可以把这几个数相加，再把它们的和与这个数相乘，结果不变。通常只用3个字母来表示：（a+b）c=ac+bc或ac+bc=（a+b）c。

四、达标检测

1.判断正误

（1）56×（19+28）=56×19+28;

（2）32×（7×3）=32×7+32×3;

（3）64×64+36×64=（64+36）×64。

2.你能说出下列算式的算理吗？选择你自己觉得较为简便的方法计算下列算式：

（40+8）x25;

24×（3+9）;

20×（99+1）;

78×102。

【设计意图：第2题的4个不同类型的计算题不仅能检验出学生对乘法分配率的理解和应用水平，还能使学生明白乘法分配率的真谛——简便计算的数学艺术。】

3.巩固提高

56×9+56×91;

83+83×99;

31×99。

【设计意图：解第3题需要的是乘法分配率的逆运算，能加深学生对乘法分配率的理解。】

五、布置作业：写学后反思

師：请写这节课所学的知识点，或是通过什么方式、方法学会了什么数学知识，或是学完本课后有哪些地方还不太懂，或是在哪些知识方面比较有心得。希望大家能尝试建构本课的思维导图。

【设计意图：以学定教，先学后教，学生不是教师教会的，而是自己学会的，让学生写学后反思不仅有利于学生建构完整的知识和思维体系，学生还可以不断总结出好的学习经验，明白自己的错误在哪里并进行改正，让自己进步。教师也可以根据学生的学习经验进行专题性的培优补差。】

六、课堂小结

师：谈一谈这节课你有什么收获。

【课后反思】

乘法分配律是人教版教材四年级下册第三单元第六课时的知识。乘法分配律包含的两个算式怎样呈现？怎样才能让学生理解算理并获得学习经验，最终归纳出乘法分配律？乘法分配率存在的价值以及如何灵活应用？……这都值得思考。

1.考虑学生如何学的问题

数学不仅仅是让学生学会一些数学符号知识，要让学生知道这些数学符号的意义，更重要的是要让学生学会发现知识、创造知识的方法。

以体育课游戏活动为背景设计的3个连续递进的问题，能让学生在经历数学活动、积累相关学习经验后，通过观察等式的特点总结出乘法分配率。

问题1的出示是为了让学生能结合图形初步理解两种方法的算理，以及体现的数学思想，知道可以运用两种方法解题。

问题2是在问题1的基础上强化学生的学习经验，使学生能运用图形和学具演示、分析，学会应用两种方法解题，加深学生对算理的理解。

有了前面积累的学习经验，学生在解决问题3时就能充分理解算理并能较为熟练地进行列式计算，总结乘法分配率。

2.设置达标检测，体现教、学、评的一致性

在教学活动中，学生参与了学习，但学会了没有？学得怎么样？学到什么水平？这是教师和学生都想知道的问题。为此我设计了3个题目：第1题是判断题，主要检测学生对公式的理解程度;第2题有4道计算题，这4道计算题不仅能检验出学生对乘法分配率的掌握情况，还能使学生感受到简便计算的数学艺术;第3题为乘法分配率的逆运算问题，亦能将学生对乘法分配率的理解水平推向一个新的高度。

（责编：童夏）