从直观经验走向数学推理

章刘飞

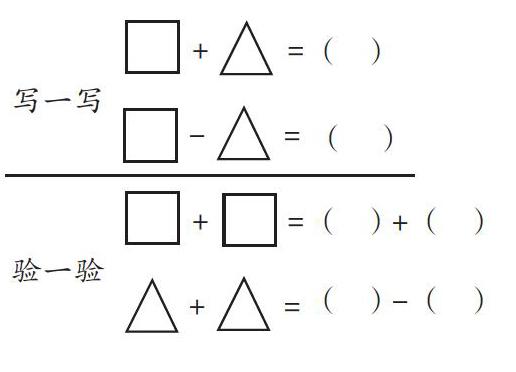
[摘要]“和差问题”是小学数学中的一个经典问题，传统教学重点是告诉学生“大数=（和+差）÷2，小数=（和-差）÷2”，缺少过程性的探究。在“和差问题”的教学中，教师基于学生从直观地凑数到一一列举再到数学推理建构新方法，让学生经历观察、分析、验证、应用的过程，可有效帮助学生积累学习活动经验，提升学生的数学推理能力，发展学生的数学核心素养。

[关键词]和差问题;直观经验;数学推理

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0052-03

人教版教材六年级下册在“数学思考”这个单元的练习中安排了这样一道题目：

〇、口、△各代表一个数，根据下面的已知条件，求〇、口、△的值。

（1）〇+口=91 （2）口-〇=8

△+口=63 口+〇=12

△+〇=46 △=口+口+〇

对于第（1）小题，常规的解答方法是把三个等式“=”左边的图形加起来，“=”右边的得数加起来，从而知道〇+口+△的和是多少，然后再求每个图形的值。还有一种方法是把前两个等式“=”左边的图形相减，“=”右边的得数相减，得到第四个等式“〇一△=28”，然后把第三和第四个等式“=”左边的图形加起来，“=”右边的得数加起来，从而得到〇+〇的和是多少，最后再求每个图形的值。

对于第（2）小题，常规的解答方法是把前两个等式“=”左边的图形加起来，“=”右边的得数加起来，从而得到口+口的和是多少，然后再求每个图形的值。当然还有一些学生是用“凑数”的方法，先思考满足“口-〇=8”的可能答案，然后再思考满足“口+〇=12”的可能答案，两个都满足要求，就得到正确的答案了。

在教学中，笔者发现学生一般喜欢用“凑数”的方“必然”的过程，让学生相信这不是一种“凑巧”，而是一种必然的经验。】

出示问题：一个笔袋和一本练习本一共12元，一个笔袋比一本练习本贵6元，一个笔袋（）元，一本练习本（）元。

交流：你是用什么方法解决这道题的？

（1）快速列举法：9+3=12，9-3=6。

（2）一一列举法：如11+1，减法不对;10+2，减法不对，9+3，减法对。

（3）笔袋+笔袋：12+6=18（元），所以一个笔袋是9元;练习本+练习本=12-6=6（元），所以一本练习本是3元。

师：你可以用自己喜欢的方法解题，但更要考虑如何既正确而又快速地求得答案。

师：那像这样的加减法算式，都有这样的秘密吗？可以举一些例子再验证一下。

（学生尝试举例证明，反馈交流）

小结并板书：大数=（和+差）÷2，小数=（和-差）÷2。

【反思：解题方法千万条，正确快速很关键。学生基于列举法学会用“和+差”和“和一差”来计算，这是一种新方法的尝试，更是一种新经验的应用。用自己喜欢的数据来进行验证这种方法的普适性，既是一种过程性的尝试，更是一种对结论的不完全归纳，体现了求真务实的科学精神。】

（四）课堂总结，拓展思维

师：今天我们通过仔细观察、积极思考，并采用多种方法找到加减法里面的秘密。数学学习就是这样，有了问题，我们就解决问题，在解决问题的过程中，又产生新的问题，只有在问题中不断寻找结果，我们的数学学习才会越来越棒。现在，你看着这张图片，你心里有新的问题了吗？

生：乘除法里的问题;减乘相关的问题;加除相关的问题……

【反思：带着问题进入课堂，最后带着问题走出课堂，这不仅是一种数学意识，更是一种学习习惯。學生只有自主思考、合作探究，才能形成数学学习的兴趣，提高解决问题的能力。】

【教学反思】

1.鼓励学生学会提问。提出问题的意识贯穿本节课的始终，可让学生养成“想一想”“问一问”“试一试”“验一验”的好习惯。学生提出的问题或许没有教师想象中的那么理想，但是，提着提着，就“提”到核心要素上去了。特别是求两种物品的单价，学生不仅直接问到点子上，而且还能用“猜测”“一一列举”等方法去解决问题。这样的学习习惯必然能促进学生能力的提高。

2.师生合作寻找规律。要得到“大数=（和+差）÷2，小数=（和-差）÷2”这个抽象的规律，必须要经历一定的探究。学生思考的重点往往是如何得到两个不同物品的单价，而至于是用什么方法求得的，没有进行思考。要使学生能通过观察、讨论、归纳、应用“大数=（和+差）÷2，小数=（和-差）÷2”这个规律，就需要师生合作，如数形结合“验一验”、开放式举例“验一验”等。

3.不断优化解题方法。在第一次尝试解决“口+△=10”的问题时，鼓励学生打破固定的“一个答案”，让学生积极参与解决问题，这样才会出现“9+1，8+2，7+3，6+4，5+5，4+6，3+7，2+8，1+9”这9种情况。学生一是结合自己的生活经验，认为这两样物品的单价可能是多少，还有就是认为两种物品的单价是固定的，所以只能有一种答案。教师再出示“口-△=2”这一条件，这时学生会尝试用减法进行一一验证，而且理所当然地提出：第一件物品是大数，第二件物品是小数，所以“5+5，4+6，3+7，2+8，1+9”都是不对的。学生对一一列举的方法是情有独钟的，甚至有些数感好的学生，一下子就想到了答案，这对建立“大数=（和+差）÷2，小数=（和-差）÷2”这个规律，是一个挑战。而且解答组合的两个等式，学生以前也是没有经历过的。为此，教师用遮挡两个小数或两个大数的方式，引导学生去观察、分析，然后再用圆片图验证，最后让学生用自己想的数进行验证，通过不断强化得出的新方法。不管是“一一列举”，还是“大数=（和+差）÷2，小数=（和-差）÷2”，在这节课中说不上哪种方法谁更好，但教师要有一种意识，即得到一种新方法的过程，就是一个学习研究的过程，对于学生探究新知识是一种经验积累。可以预见，对于解决数据比较大的“和差问题”时，用“大数=（和+差）÷2，小数=（和-差）÷2”还是比较好的。

（责编：黄春香）