“读”“说”“查”，作业检查的三字经

方经斐

[摘要]学生完成作业后回头进行检查，这一环节是不可缺少的。检查实质上就是反思，对自己的作业进行审查反省，就有可能发现错误，从而获得更正的机会。教师要教会学生反思与反省，这对学生学习品质的提高乃至人生成长都具有深远影响。

[关键词]读;说;查;再次;机会;更正

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0041-02

笔者一直从事低年级数学教学工作，发现低年级学生（尤其是一年级学生）的作业中几乎都会出现一些共性问题，如計算题错误常有雷同，填空题错误率居高难下，选择题是连蒙带猜、不明就里，解决问题是“重灾区”，等等。为了减少学生上述作业中的错误，笔者针对性地采用了“读”“说”“查”的作业检查三字经，效果斐然。

一、读

“读”，顾名思义就是读题。只有会读题、读通题、读懂题，才能明白题目讲的是什么事情，待求的是什么问题，由此施以对策，解决所求问题。

低年级学生，尤其是刚入学不久的一年级学生，有些题并不一定是不会做，而是由于识字量非常有限，读不懂题目里的文字，也就不明白题目想表达的意思。再就是平时的作业或期末测试，一般都有教师帮助读题，到了一年级下学期，要求学生自己读题和解题时，原来依赖教师读题的习惯还未彻底消除，学生没有耐心自己读题，题目中的文字也认不完全，由此产生了畏难情绪，做题出错也就不足为奇了。针对上述状况，笔者在平时的教学中强化培养学生独立读题的习惯，主要措施如下。

1.给予机会，磨炼读题

“万事开头难。”教师千万不能因为怕学生不会读题、读不通题、读题速度慢、读题出声而影响他人等，就越俎代庖，长此以往，就会培养出懒惰的学生。教师有时要学会“偷懒”，把读题的机会交给学生，让学生自己磨炼读题，教师则在一旁倾听、点评和指导。在读题的过程中，当学生遇到不认识的字时，教师可以帮助注上拼音。学生在拼一拼、读一读、记一记中认识的字越来越多，读题的能力就会越来越强，计算解题的正确率也会随之提高。

2.精确读题，读懂题目

心理学研究表明，儿童具有感知事物笼统、不精确、顾此失彼等特点。因此，在做填空题和解决问题时，学生读题常常是一扫而过，或凭借以往的经验，陈陈相因就动笔了。而此时的题目并非他们想象“经验”里的原型，计算的方法自然也不同，故而时常出错。

教学时，笔者要求学生用手指着题目，一个字一个字地精确读，出声读、轻声读、静默读皆可，尽力做到读仔细、读完整、不漏字、不添字，在读通题、读懂题、弄清题意后，方可动笔解答。

如，教学“数的组成”时，有一组填数题：（1）（）个十和（）个一合起来是23;（2）23里面有（）个一和（）个十。这两道题文字表述相近，数字相同，学生往往不多加细读，就把第（1）题中填的数同样填在第（2）题中，导致解答错误。

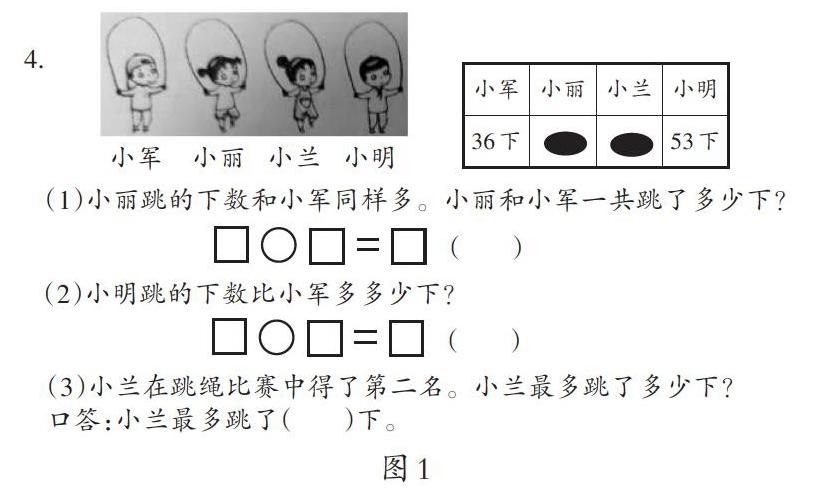
又如图1中的解决问题，在读第（1）题时，要求学生精确读出“同样多”，并引导学生思考：“同样多”是什么意思？这里的“同样多”是与谁“同样多”？在读懂题目后，再要求学生在“同样多”的文字下面注明“36"，将隐含的条件显露出来，变未知为已知，从而提高学生解题的准确率。

二、说

“说”，是指说题意、说方法、说思路。语言是思维的外壳，会做未必真正理解了，会说也很重要。通过学生的语言表述，教师可以发现问题，进而解惑授业。做题不仅仅是为了得出答案，同时也是培养学生思维能力和语言表达能力的有利时机和有效途径。

1.说图意

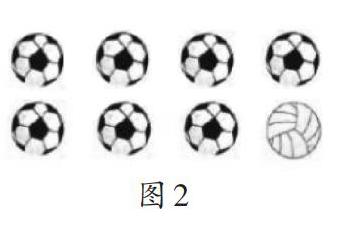
如，教学一年级上册看图列式时，教师出示例题：根据图2列出两道加法算式和两道减法算式，并说说题意。学生在写加法算式时，一边写算式7+1=8和1+7=8，一边说图意：“有7个足球，1个排球，一共是8个球;有1个排球，7个足球，一共是8个球。”在写减法算式8-7=1和8-1=7时，学生同样能说出图意：“一共有8个球，去掉7个足球，还剩1个排球;一共有8个球，去掉1个排球，还剩7个足球。”

又如，教师出示图3、图4，要求学生先说出图意。学生说：“图3中，盘子里面有5个苹果，盘子外面有3个苹果，问号处是求一共有多少个苹果，就是把盘子里面的5个苹果和盘子外面的3个苹果合起来，用加法计算，即5+3=8（个）。图4中，一共有7个羽毛球，球桶外面有1个，要求球桶里有多少个羽毛球，就是从一共有的7个里面去掉1个，用减法计算，即7-1=6（个）。”

2.说算法

计算时，教师可以要求学生一边计算一边说算法、说法则，做到手写口说、做说合一。

如，教学一年级下册“100以内的加法和减法（二）”时，主要是学习进位加法和退位减法的知识。这是学生第一次遇到进位和退位，他们的大脑中原本没有进位和退位的意识，不熟悉进位与退位的方法，稍不留心就会出错。针对这一状况，在用竖式计算时，教师可要求学生边计算边说算法、说法则、说过程。如计算54-17=？时，学生可以边算边说：“54减17，个位4减7不够减，从十位退1当十，14减7等于7，十位上的5退1还剩4，4减1等于3，得数就是37。”

如此经过较长时间的训练，学生计算的出错率会大大降低。

3.说思路

学生对题目的理解与否，通过语言的表述便能知晓，只有理解了内容，才能用自己的语言表述题意，才能厘清解题的思路。

如，教学图5、图6的解决问题时，可以让学生先说：“图5中，求一共有多少个键，就是把白键和黑键合起来，用加法计算，即52+36=88（个）。图6中，求已经栽了多少棵，就是从一共要栽的总棵数里去掉还没有栽的棵数，用减法计算，即35-4=31（棵）。”

通过说思路，可以不断提高学生的分析能力和思维能力，同时锻炼学生的语言表达能力。

三、查

“查”，是指检查验算、再度审视。学生在首次计算解题时，可能会因一时疏忽，或理解偏差，或暂时思维“短路”，或书写笔误等造成错误。回头进行检查，就可能会豁然开朗，发现计算错误之处，有重新更正的机会。

由于低年级教学内容相对浅显，涉及的计算也较简单，学生计算起来速度还是比较快的，可以有充足的检查时间，重点是如何培养学生的检查习惯？

1.查得数，再次计算

首次计算的得数，一般都不能保证百分之百正确，经过检查和再次计算，可以提高得数正确的概率。如，做“直接写得数”“计算题”等练习时，笔者都要求学生重新算一遍;做“竖式计算”时，则要求学生先查看数字、运算符号是否抄写有误，再重新计算，最后比较两次计算的得数，看看是否相同。

2.查填空，再次读题

“填空题”考查的多是概念或容易混淆的内容，这也是学生错误高发之处。检查时，教师应要求学生反复多读原题，弄懂概念、厘清关系之后审慎填写。

如，做"50比（）大1，比（）小1”的填空题时，不少学生误将题目看成“比50大1是（），比50小1是（）”，导致填写错误，通过再次仔细读题，学生发现了错误所在。

又如，做"49添上1是（）个十”的填空题时，不少学生只读到"49添上1是（）”，后面的“个十”就省略不读了，故误填成“50”，当再次仔细读题时，发现了错误所在。

3.查条件和问题，再次思考

“解决问题”一直以来就是学生的“重灾区”，原因无外乎是对文字内容的理解有偏差，没有找到数量之间的关系、算式的对应选择和思维分量的增加等。当学生第一次列出算式解答后，教师应引导学生重新查清条件所对应的问题，厘清数量间的关系，选择相应的算式等，简单来说就是再理理思路、再次思考、深度理解。

如，解决“小红和小组里的每个同学都合照一次，一共照了9次。小组里一共有（）人。”时，一年级学生往往读到“照了9次”，就誤以为是9人，故不多加思考地就填上“9”。这时，教师要求学生重新查找题目中的条件和问题。学生通过再次审慎思考和画直观图后得知，已知条件是“小红和小组里的每个同学都合照一次”“一共照了9次”，问题则是“小组里一共有多少人？”，这其中还应该包括小红本人，也就是9+1=10（人）。通过“查”，学生自己找出了错误，更正了答案。

总之，学生在完成作业后进行检查是不可或缺的。检查就是反思，更是反省。教师要培养学生检查作业的习惯，结合上述“读”“说”“查”的作业检查三字经进行反思与反省，从而有效降低学生作业的出错率，提高学生的学习成效。

（责编：李琪琦）