借直观小方块，深度建构面积计算

陈肖娟

[摘要]建构深度课堂，要抓住知识的本质和内涵。“长方形和正方形的面积计算”是图形面积教学的种子课。在图形面积教学的起始课中，借直观的小方块，让学生通过“悟——测——验——用”四步，由浅入深，循序渐进地探究长方形面积计算的本质与内涵，以求课堂的深度建构。

[关键词]面积计算;小方块;准确定位;深度建构

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0021-02

一、源于实践之思

思考一：周长和面积为何易混淆

学生常常混淆周长与面积，如果是面积计算与面积单位换算的综合运用，错误率更是居高不下，原因如下：一是知觉错误，由于周长和面积都在一个图形之中，导致认识易混淆;二是符合学生易忘记的认知规律;三是符合学生的心理特征——易混淆面积表征与长度表征或周长表征。

思考二：学生的困惑何在

學习“长方形和正方形的面积计算”时，学生能快速背诵公式和熟练地运用公式进行计算，可是对于“长方形的面积为什么等于长乘以宽？”，学生却十分困惑。究其原因有二：一是教师只注重公式的推导与应用，忽视用面积单位度量图形的过程，过早进行形式化的计算训练;二是课堂定位的偏差，教师只要求学生牢记公式、熟练应用，忽视学生学习经验的积累过程。

长方形面积计算的学习难在哪里？下功夫的点在哪里？

二、探寻课堂之深

如何展开教学才能建构深度课堂？通过“悟——测——验——用”四步，由浅人深，带领学生探究长方形面积计算的本质。

（一）悟“面积”——比中明理，感悟本质

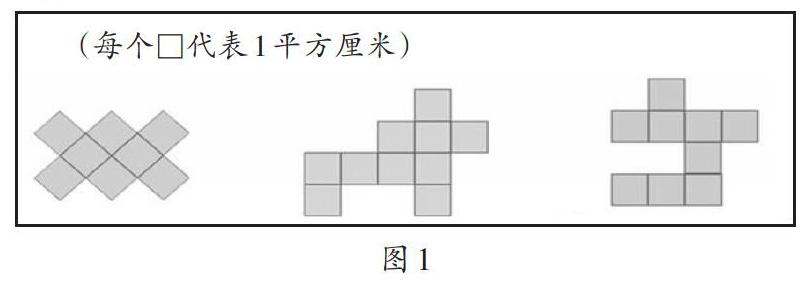
学习是一个从眼睛走向大脑、从观察走向思考的过程。课始，教师提问：“下面3个图形（如图1），哪个面积最大，哪个面积最小？说一说理由。”通过比较图形的面积大小，激活学生数面积单位的经验，在观察、比较、归纳的过程中，学生能够感知一个图形的面积就是数一数它有几个小方格，在对比中感悟图形的面积本质。

（二）测“面积”——拼摆探析，领悟本质

度量是面积计算的本质，通过“动手拼摆——问题驱动——深入追问”三个维度，带领学生逐渐领悟长方形面积的度量本质。

1.动手拼摆

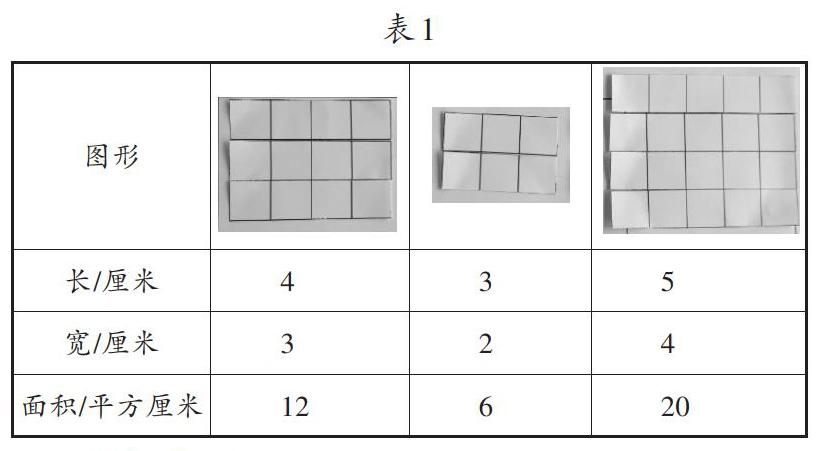
思维是从指尖开始的。活动一：让学生任意取几个1平方厘米的正方形拼成不同的长方形，并记录在表1中，再和同桌说一说有什么发现。这样，学生在拼摆中初步感悟：面积是几，就要摆几个小正方形，每行摆几个就是长方形的长，摆几行就是长方形的宽;每行的个数×行数=正方形的总个数，也就是图形的面积。拼摆长方形能直观地为学生打通为长、宽与面积单位个数的联系，不仅让学生知其然，亦知其所以然，凸显面积计算的本质。

2.问题驱动

思源于问，问题驱动是激发学生积极探究和深度思考的支点。活动二：动手摆一摆、分一分、画一画，求出下面长方形的面积。学生动手验证，用1平方厘米的正方形把长方形铺满，每行摆5个，摆了4行，长方形的面积就是20平方厘米（如图2）。在数的过程中，学生发现最简便的数数方法——把每行的5个×4行就可以得出总个数，从中感悟图形的面积就是数有几个1平方厘米的正方形，深刻理解长方形面积的本质。

3.深人追问

教师的追问要抓住问题的本源，要围绕问题的本质，让学生在追问中讲理，在辨析中明理，在理中逐渐掌握长方形面积计算的本质。活动三：如果只铺一部分，你能数出全部面积单位的个数吗？在深人的追问中，学生明确知道“尽管只铺一部分，也能数出图形一共有几个小正方形。学生在观察、想象、分析活动中，领悟到长方形中所含面积单位个数与每行个数、行数之间的联系。至此，突破本节课的教学重难点。

（三）验“面积”——探索内涵，建构本质

1.想象提升

想象提升：长方形中只摆了5个1平方厘米的正方形，你能数出长方形有几个1平方厘米吗？学生通过观察、对比、想象，知道把正方形向下平移，就表示每行摆了5个，把正方形向左平移，就表示每列摆了4个;接着教师将正方形演变成刻度，从单位面积向单位长度转化，建立长度单位和面积单位之间的对应关系，提升学生的思维能力。这样，数形结合，沟通了长、宽与每行面积单位个数、行数之间的关系，使学生的思维从朦胧走向清晰。

2.再次抽象

再次抽象：你会数如图4所示的图形的面积吗？借助几何直观，学生经历了“铺满——未铺满——空白图形”的过程。通过直观数数到想象数数，从直观到抽象，从朦胧走向清晰，为学生的思维打开通道。长的长度就是沿长摆几个面积单位，宽的长度就是沿宽摆几行的对应关系，建构了长方形的长、宽与面积单位的个数的联系，避免学生以后生搬硬套计算公式。

3.沟通联系

变一变：长方形的长缩短1分米，它的面积是多少？学生交流汇报后得出“长方形的面积=单位面积的每行个数×行数”;正方形是特殊的长方形，它们是不可割裂的（如图5）。学生的思维从混沌走向明朗，使得公式的推导水到渠成。

（四）用“面积”——灵活训练，深化思想

1.拓展延伸

猜一猜：一个面积10平方厘米的长方形，它的长和宽各是多少？学生在问题的驱动下，积极参与，得出“长为5厘米，宽为2厘米;长为10厘米，宽为1厘米”。此时教师可追问：“长方形的长有可能比10厘米长吗？”打破学生的思维定式，同时突破以“整个”面积单位数的常规思维，让学生更深入地理解长方形面积的意义。

2.变式延伸

猜测是学生喜欢的活动，最后让学生猜一猜：信封里藏的长方形面积是多少？在学生随意猜测后给出提示：一行有3个，摆了2行。学生猜：6平方厘米，6平方分米，6平方毫米。结果学生发现都猜错了。巧妙改变度量标准，让学生在错中辨析，在错中明理，避免了学生思维的惯性，驱动学生在思辨中深入理解长方形面积的本质，深刻建构长方形的面积公式。

教材是教学的源，学生是教学的因，抓准教学的“源”与“因”，才能引导学生深度探究，经历数学模型的建构，有效培养学生的深刻思维。