基于数据分析教出平均数的统计学“味道”

郑祥旦

[摘要]基于数据分析观念，呈现平均数的统计学“味道”的教学，就是要把每个数据看成是抽样得到的独立样本，对统计图表中的数据进行统计分析，得出的数据误差有正有负，在正负抵消为零时得到平均数的概念理解和算法理解，以促进学生理解平均数的统计意义。

[关键词]平均数的教学;基于数据分析;统计学

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）14-0019-02

平均数是一个重要的统计量。目前，小学数学关于平均数的教学已经从简单的应用题发展到系统的统计初步知识，即启发学生去想到“移多补少”，将“和”按人数“平均”，以平均数来代表一组数据的整体水平，体会平均数具有假设性的特征，从而比较浅显地揭示平均数的统计意义。随之而来的问题是，很多教师过早地给出平均数的统计意义，甚至出现抽象的“虚拟数”概念，超出了学生接受和理解的范围，失去了统计学的“味道”。因此，有必要运用“数据分析观念”去重新审视平均数的教学。

一、教材分析

小学的平均数一般是指算术平均数，也就是一组数据的和除以这组数据的个数所得的商。算术平均数常用于表示统计对象的一般水平，它是描述数据集中程度的一个统计量，用平均数表示一组数据的情况，有直观、简明的特点。

人教版四年级下册的教材设置了两道例题。例1是先直接求平均数，再用统计图表示每人收集到矿泉水瓶的数量，通过观察得出平均每人收集了13个，然后用算式表示平均数与一组数据之间的关系，归纳求平均数的一般方法，得到平均数的含义。教学时，学生根据生活经验进行“移多补少”，从平均数应用题进行迁移，往往缺少数据分析过程。例2是比较两组个数不同的数据，通过问题“哪个队的成绩好”，使学生感受用总数表示各队成绩的比较方法不公平，得出应用平均数区别这两组数据的总体情况。教学若从例1到例2，学生一般不会再用“求总数”的方法来比较，而是直接迁移求平均数的方法。因此，可反其道而行之，用例2的踢毽比赛为素材导入新课，再教学例1认知平均数，而后又返回到例2来拓展学生对平均数的理解，这样的教学反而能收到良好的教学效果。

二、教学过程及相应评析

平均数教学关键之一是发展学生的数据分析观念，使他们愿意用平均来刻画数据。因此，本课的教学目标可确定为：通过解读图表进行简单的数据分析，学会求平均数的算法，体会平均数的统计意义。

1.利用学生踢毽比赛的情况，在独立样本的比较中引入新课

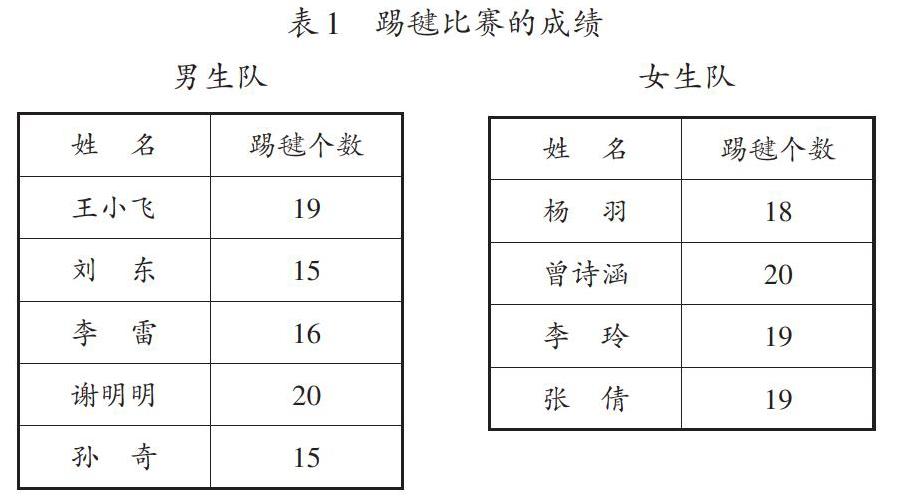
教师先出示踢毽比赛的主题图（例2），让学生猜一猜男生队和女生队哪个成绩好，然后模拟比赛场景，依次给出每一对同学的比赛成绩并记录于统计表中（表1），并顺次征询胜负情况，让学生用自己的语言解释统计结果，根据结果做出简单的判断后进行交流。

在出示第5个男生踢毽的成绩后，有学生认为，男生队的个数多，成绩好。有学生认为，两个队的人数不同，这样比赛不公平。于是，学生根据课前的预习成果，提出要计算每队的平均成绩。这时，教师可板书课题，然后出示例1。

【评析：教学统计意义上的平均数，必须考虑到样本的随机性，每个数据都可看成独立的样本，是通过抽样得到的，而且每次抽样是独立进行的，每次抽样过程在本质上是一样的。教师要发展学生的数据分析观念，就必须在特定的情境中促使学生想到用平均数，愿意用平均数来解决问题。】

2.利用收集饮料瓶的情况，在误差的学习中掌握平均数的知识

（1）数据分析，移多补少，概念理解

教师出示环保小组收集饮料瓶个数情况的统计图（例1），引导学生找出数据的一些简单特征：小亮收集11个是最少的，小明收集15个是最多的，小红比小兰收集的多2个，等等。

进一步挖掘数据的深度特征：小明送2个给小亮，两人收集的个数同样多;小红送1个给小兰，两人收集的个数也同样多。送完之后，4人收集的个数都是13个。换一种说法，小明比13个多2个，而小亮比13个少2个;小红比13个多1个，而小兰比13个少1个。多的送给少的，多与少互相抵消了，还得到一个新的表示同样多的数，13成为這4个数的代表。

归纳概念的含义：数学上，把这种数的代表13称之为平均数。也就是说，13是这4个数的平均数。也可以说，平均数是一组数据平均水平的代表。

（2）寻找观测数据和真实数据的关系，理解算法

教师通过问题“13是这4个数的代表，那么怎样用算式表示13与这4个数的关系？”引导学生理解数据间的相等关系，即13x4=14+12+11+15;进一步推算，把平均数当作未知数，就得到（14+12+11+15）÷4=13;归纳算法，得出求几个数据的平均数，就是“和÷几=平均数”。

学生可能会疑惑：平均数与平均分有什么关联？对此，教师可引导学生回顾平均分的过程，如把52个瓶子平均分4份，每份是几个，即每次拿出4个，一个一个地分;或者一次拿出40个，十个十个地分，直到分完为止。与此不同，求平均数只要把多的“匀”给少的就可以。小结：平均数与平均分虽是一个字之差，但它们的意思大不相同。

【评析：平均数的教学，重要的不是让学生掌握计算模式“平均数=瓶子总数÷人数”，而是让学生在分析数据中感悟平均数的价值，产生需要用平均数来刻画数据的意愿。平均数的概念与算法相生相伴，算法的表达是出于对数据误差的理解，而不是出于对平均分的拓展。倘若教学直奔求平均数而去，学生就只学会“移多补少”“计算方法”这些单纯的数字计算，而使平均数失去统计学的“味道”，那就不是统计初步知识的教学。】

3.遭遇统计需要，体会平均数的意义和价值

如何让学生在学习后能想到用平均数，可让学生回到例2的求平均数的问题。

（1）移多补少

再次观察两组数据，学生能快速地发现女生队的平均数是19个，“移多补少”即可。

（2）算式表达

男生队的数据复杂，难以用“移多补少”快速找出平均数，可以把平均数当作未知数，列算式（19+15+16+20+15）÷5=17。

（3）统计理解

平均数需要从“算法”“概念”“统计”这三个角度来理解。

教师提问：“现在，女生队来了第5个同学——李丽红，她可能踢毽多少个？”学生根据前4个同学的平均数，猜测她可能踢毽19个。

教师满脸遗憾地说：“因为第5个同学李丽红表现不佳，导致女生队失败。你们能计算李丽红的成绩吗？”学生根据数据之间的关系，列出算式18+20+19+19+（）=16x5，得出李丽红可能踢毽4个。教师追问：“她只可能踢4个吗？”学生经过思辨，得出她的成绩可能是1～8中的一个。至此，为平均数是小数的教学打下伏笔。

【评析：概念理解和统计理解对于统计的教学是非常重要的。教学时，通过女生队失败的情形，学生深刻地体会到：①平均数可以用来作为推断的重要依据;②平均数反映的只是一般情况，但不排除特殊情况的出现。这样，学生既体会了平均数的意义，又体会了数据的随机性。】

三、教后反思

用比较两组个数不同的数据导人平均数的教学，较早出现于吴正宪老师的课堂，她精湛的教学艺术，使学生从中感受到学习数学的快乐。我仿照吴老师的做法，以例2的踢毽比赛为导入新课的素材，一对一对地呈现两组比赛的成绩，学生的思绪就在一一对比和总数对比、可行与不可行之间摇摆，最终产生要比较平均数的需求。例1的教学，是把每个数据看成抽样得到的独立样本，对统计图表中的数据进行统计分析，得出数据误差有正有负，由正负抵消为零得到平均数的概念和算法，然后再理解平均数的统计意义。再次教学例2时，学生对学习对象有了更高的认知，可以根据数据的特征，求女生队的平均数时“移多补少”，求男生队的平均数时列式计算，这是运用知识求解的本真。作为对知识的拓展，还可增加女生队人数后让学生求其平均数，使其体验随机现象。总之，这种基于数据分析的教学才真正体现了平均数的统计学“味道”。