扩展的卡尔曼滤波在近红外光谱提取脑血流信号中的研究
刘颂阳, 刘光达, 刘卓娅, 邱吉庆, 蔡 靖,朱展鹏, 张 程, 齐 远, 张 尚
1. 吉林大学, 吉林 长春 130061 2. 吉林大学珠海学院, 广东 珠海 519041 3. 吉林大学第一医院, 吉林 长春 130061
引 言
大脑作为人体的神经中枢, 是人类高级认知功能的载体。 近年来, 用于研究大脑运作机制、 疾病诊断的脑功能成像方法得到了长足的发展, 脑功能成像技术主流的方法有脑电图(electro encephalo gram, EEG)、 脑磁图(magneto encephalo graphy, MEG)、 功能磁共振成像(functional magnetic resonance imaging, FMRI)、 功能性近红外光谱技术(functional near infrared spectroscopy, FNIRS)等。 在上述方法中, 功能性近红外光谱技术(FNIRS)因具有较高的空间分辨率、 适中的时间分辨率、 无创费用低等优点成为脑功能成像技术研究的热点。 各种脑成像技术优劣对比见表1。
功能性近红外光谱技术(functional near infrared spectroscopy, fNIRS)探测脑组织活动的方式是间接方式。 大脑的各种神经活动需要氧气, 脑部血流(Celebral blood flow)做为大脑供氧的重要渠道, 它对大脑的神经活动是十分敏感的, fNIRS正是利用探测脑血流动力学的参数变化, 来判断脑组织的各种神经活动的。 显而易见的是, 大脑作为人的神经中枢, 各种生理活动如心跳、 呼吸、 脉搏等都会引起神经活动, 也自然会引起脑血流动力学的参数变化, 因此, 如何从包含各种生理干扰的信号中提取脑组织神经活动信号是近红外光谱提取脑功能信号难点。

表1 各种脑成像技术优劣对比
目前, 常见的提取近红外光脑信号的算法有: 脉搏色素谱法[1]、 EEMD-ICA法[3]主成分分析法(PCA)[5]、 独立成分分析法(ICA)[6]、 相干平均法[7]、 自适应滤波[8]等。 脉搏色素谱法采用注射显影剂吲哚青绿的方式进行示踪估计; EEMD-ICA对信号进行希尔伯特变化, 再进行滤波; PCA和ICA这两种方法适用于连续光谱的近红外光谱系统; 自适应滤波法可以消除心跳干扰; 相干平均法可以滤除脉搏等生理干扰。 上述算法在对近红外脑神经活动信号提取时都取得了一定的进展。
但是, 上述算法在提取近红外光谱脑功能信号时, 重视各种生理干扰, 忽视了在提取信号中的测量干扰, 如仪器精密度、 信号传输中的串扰等。 研究[10-11]表明, 近红外光谱脑信号用非线性算法提取可以去除测量干扰。 如Fritson使用非线性算法将信号Volterra[11]级数化, 大大提高了信号的信噪比。 本工作提出的扩展的卡尔曼(Extend Klaman Filter, EKF)算法是一种非线性算法。 根据近红外光谱提取的脑信号中的干扰成分是多维非平稳随机的, 利用其时变性、 功率谱不固定, 建立了数学模型, 将信号进行泰勒级数分解, 取一阶函数, 再进行滤波和估计, 进行了高斯(Gauss)滤波实验、 Valsava实验、 视觉诱发实验, 并将EKF算法和主流的EEMD算法进行比对。
1 理论基础
1.1 修正的朗伯比尔定律
朗伯比尔定律(Lambert-Beer law)是分光光度法的基本定律, 是描述物质对某一波长光吸收的强弱与吸光物质的浓度及其厚度间的关系。 适用于所有的电磁辐射和所有的吸光物质, 包括气体、 固体、 液体、 分子、 原子和离子。 其公式为
(1)
式(1)中,ελ为吸光物质在波长λ(nm)下的消光系数,c为吸光物质的浓度(mol·L-1),d为光在物质中的传输距离,I0和I分别代表出射、 入射光强,A为吸光度。
但事实上, 光在生物组织中会有散射、 吸收等现象, 图1给出了光在组织传播的路径。 因此, 光在组织中的实际传输距离远大于物质厚度。 为了消除这一误差, 1998年, Deply D T等对朗伯比尔定律进行了修正[12], 修正的朗伯比尔定律见式(2)
(2)


图1 光在组织中的路径
1.2 功能性近红外光谱
近红外光谱是指波长在650~950 nm的不可见光, 科学家Jobsis[2]在1977年发现近红外光对人体组织具有良好的透射性, 首次验证了用近红外光谱技术无创监测组织血氧的可行性。 各种生理活动都离不开氧气, 脑组织所需氧气的输送靠的是脑血流中的两种血红蛋白, 氧合血红蛋白(Hb02)和还原血红蛋白(HbR), 当脑血流流经脑组织时, 血液中HbO2释放氧气, 供脑组织使用, HbO2转化为HbR; 当血液流经肺泡时, HbR又获得氧气转化为HbO2。 两种血红蛋白的总量基本恒定, 由上述可知, 人脑组织的生理活动会引起HbR和HbO2两种血红蛋白含量[6]的变化。
人体大脑组织中, 水的含量占据了大部分的比重, 约为75%, 除此之外, 还有氧合血红蛋白(HbO2)、 还原血红蛋白(HbR)和黑色素等。 在650~950 nm近红外光波段, 水的吸收率很低, 氧合血红蛋白(HbO2)和还原血红蛋白(HbR)的吸收率较高, 不同物质对不同波长的光的吸收度如图2, 这一区间也称为光窗期。
近红外光谱脑信号提取技术正是基于待测组织中的水、 氧合血红蛋白(HbO2)、 还原血红蛋白(HbR)在近红外波段具有不同吸收光谱特性, 以及近红外光可以穿过0.5~3 cm的外层生物组织到达脑组织这一特性进行测定的。 若分别选取波长为λ1和λ2的近红外光源, 利用修正的朗伯比尔定律,可得入射光和出射光的光密度变化, 见式(3)—式(6)

图2 组织的吸光度图谱
(3)
(4)
进而计算, 可得。
(5)
(6)
式中, ΔA是光密度变化,ε是某一物质在某一波长的消光系数,L是光源和光源接收器的距离, DPF和L的乘积可以近似表示光在组织中走过的实际路径, Δc代表的是浓度变化。 进而计算可得氧合血红蛋白(HbO2)和还原血红蛋白(HbR)两种物质的浓度变化。
2 扩展的卡尔曼滤波算法及近红外光谱模型的建立
2.1 卡尔曼滤波算法
卡尔曼滤波(Kalman filtering)是1961年由Rudolf Kalman提出, 是一种利用线性系统状态方程, 通过系统输入输出观测数据, 基于误差平方和最小的原理进行递归计算的方法, 其本质是参数化的beiyesi模型, 通过对下一时刻系统的初步状态估计以及测量得出的反馈相结合, 得到该时刻无限逼近真实值的状态估计。 在现代随机最优控制和随机信号处理技术中, 信号和噪声往往是多维非平稳随机过程, 对于离散域线性系统, 其线性系统状态预测方程式
xk=Axk-1+Bxk-1+wk-1
(7)
p(w)~N(0,Q)
(8)
cov(w)=E(wwT)=Q
(9)
式中,xk和xk-1分别为在k时刻、k-1时刻的状态值,uk-1为在k-1时刻的控制输入,wk-1为过程噪声, 并且服从高斯分布;A为状态转移系数矩阵,B为控制输入的增益矩阵,Q为过程激励噪声的协方差矩阵。
测量方程为
Zk=Hxk+vk
(10)
P(v)~(0,R)
(11)
cov(v)=E(vvT)=R
(12)
式中,Zk为k时刻的测量值,Vk为测量噪声,H为测量矩阵,R为测量噪声协方差矩阵。 并且满足:E(w)=E(v)=0。
2.2 扩展的卡尔曼滤波及模型建立
扩展的卡尔曼滤波是在卡尔曼滤波的基础上, 将非线性系统函数作泰勒(Taylor)级数展开, 再进行线性的卡尔曼滤波, 这就是扩展的卡尔曼滤波(extend Kalman filter, EKF)。
考虑离散时间非线性动态系统
(13)
其中,w(k)是过程噪声, 协方差是Qk;Vk是测量噪声, 其方差是Rk+1。f是状态变量x和时间k相关的非线性函数,h是状态方程中与状态变量x和观测量z相关的非线性函数。 进行泰勒(Taylor)展开, 取展开后的一阶线性部分作为非线性模型的近似。
状态方程表示为
=Fk-1xk-1+wk-1+uk-1
(14)
式(14)中,f(xk|k)进行泰勒展开,
(15)
(16)
测量方程表示为
=Hkxk+Vk
(17)
式(17)中, Gh(xk)表示在xk|kG处进行泰勒展开,
(18)
参考经典卡尔曼滤波的推导过程, 可以得到扩展卡尔曼滤波的五个方程式(19)—式(23)
xk|k-1=f(xk-1|k-1)+wk-1
(19)
pk|k-1=Fpk-1|k-1FT+Q
(20)
Kk=pk|k-1HT(Hpk|k-1HT+R)-1
(21)
xk|k=xk|k-1+Kk(Zk-h(xk|k-1))
(22)
pk|k=(1-kkH)pk|k-1
(23)
式(19)是状态预测方程, 式(20)是误差协方差方程, 式(21)是卡尔曼增益方程, 式(22)是滤波校正方程, 式(23)是误差协方差更新方程。
2.3 EKF模型的建立
简而言之, 人脑的神经活动需要氧气, 氧气需要脑血流中的两种血红蛋白进行输送, 必然会引起氧合血红蛋白(HbO2)和还原血红蛋白(HbR)浓度的变化。 由扩展的朗伯比尔定律及近红外光谱的特性可知, 这种变化可以由近红外光谱测量得到, 此时测量的数据是包含了生理噪声和测量噪声, 将测量所得到的数据经扩展的卡尔曼滤波, 取得HbO2和HbR浓度的变化。 图3表述了上述关系。
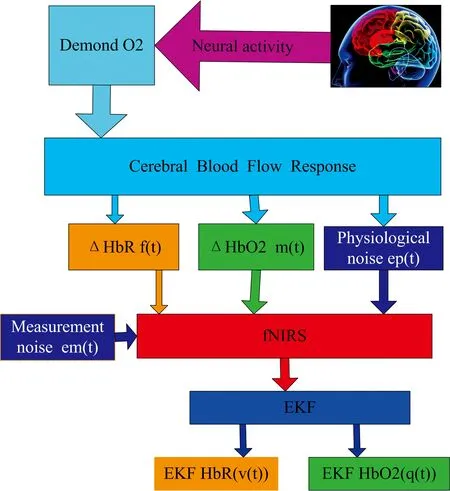
图3 脑血流动力学数学模型图
3 实验结果与讨论
3.1 扩展的卡尔曼滤波(EKF)对Gauss噪声滤波有效性的仿真实验
近红外光谱脑信号采集过程中的噪声干扰符合高斯分布, 取干扰信号w(k)和测量噪声信号v(k)的幅值均为0.01的高斯白噪声信号, 输入信号幅值为1.0、 频率为1.5的正弦信号。 使用EKF实现信号的滤波, 取Q=1,R=1。 仿真时间是5 s, 在MATLAB中编程进行仿真, 图4是在信号中叠加了高斯(Gauss)噪声的波形图, 图5是经EKF滤波后的信号。 从MATLAB仿真结果看, 信号平滑、 无失真、 没有畸变, 该算法在去除高斯(Gauss)白噪声方面效果明显。
3.2 EKF提取HbR和HbO2浓度变化
3.2.1 实验装置
为了测量整个前额叶区域的血红蛋白和还原血红蛋白的变化量, 设计了近红外光谱脑信号采集装置。 其中, 直流稳压电源和光源驱动电路给近红外光光源稳定供电, 光源为波长750和830 nm的二极管近红外光源, 用同相放大和低通滤波做初步处理, 将处理后的信号发送至上位机, 上位机用C#编写, 其框图见图6。
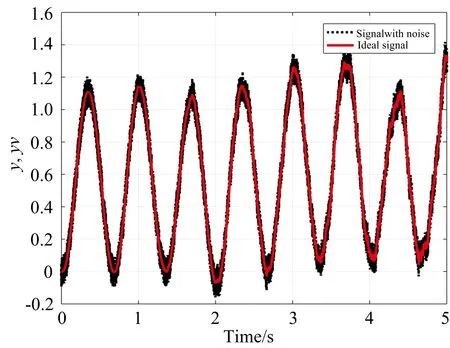
图4 叠加噪声的原始信号

图5 EKF滤波的信号

图6 装置设计框图
3.2.2 Valsava实验与分析
为了获得HbO2和HbR在血液中的浓度变化曲线, 使用波长分别为750和830 nm的近红外光源进行Valsava实验, 近红外光源和光源探测器用黑布完全遮起来, 被试者是25岁成年男性, 身体健康, 无烟酒嗜好。 耳朵中放置隔音棉, 尽可能减少外界环境干扰, 进行闭气-呼气实验。 在实验开始的0~60 s, 被试者正常呼吸; 第60~120 s, 被试者闭气; 第120 s之后, 被试者恢复正常呼吸。 采集到的HbO2和HbR经扩展的卡尔曼滤波后变化曲线如图7所示。

图7 Valsava实验血红蛋白变化曲线图
3.2.3 视觉诱发实验与分析
为了验证本方法在提取氧合血红蛋白(HbO2)和还原血红蛋白(HbR)浓度变化的对外界刺激的敏感性, 进行视觉诱发实验。 Arturs发现, 视觉诱发实验会引起脑血流参数的变化[14], Zaletel发现视觉诱发实验和脑血流流速变化是正相关关系[15]。 本工作采用黑白相间的图片作为视觉诱发源, 如图8所示。

图8 视觉诱发源
将视觉诱发源信号在电脑屏幕上交替播放, 交替频率是5 Hz, 近红外光源和光源探测器用黑布完全遮起来, 被试者是25岁成年男性, 身体健康, 无烟酒嗜好。 耳朵中放置隔音棉, 尽可能减少外界环境干扰。 让被试者观看图片, 测得氧合血红蛋白(HbO2)和还原血红蛋白(HbR)浓度变化如图9所示。
3.3 EKF和EEMD算法比对
EKF算法在提取近红外光脑信号的有效性得到了验证, 进一步对其滤波效果进行评价, 比对方法是利用均方根误差RMSE (root mean square error)、 相关系数r(correlation coefficient)。 RMSE可以表示测量值和真值的离散情况, 参数越小, 表明滤波效果越好。r表示的是相关系数,r越接近1,表示效果越好。 对同一被试者采集10组数据, 分别计算EEMD算法和EKF算法的RMSE值、r值, 结果如表2。 可以看出, EKF算法对比EEMD算法, 其RMSE值提高了0.96%,r值提高了0.6%。

图9 视觉诱发实验血红蛋白浓度变化曲线图
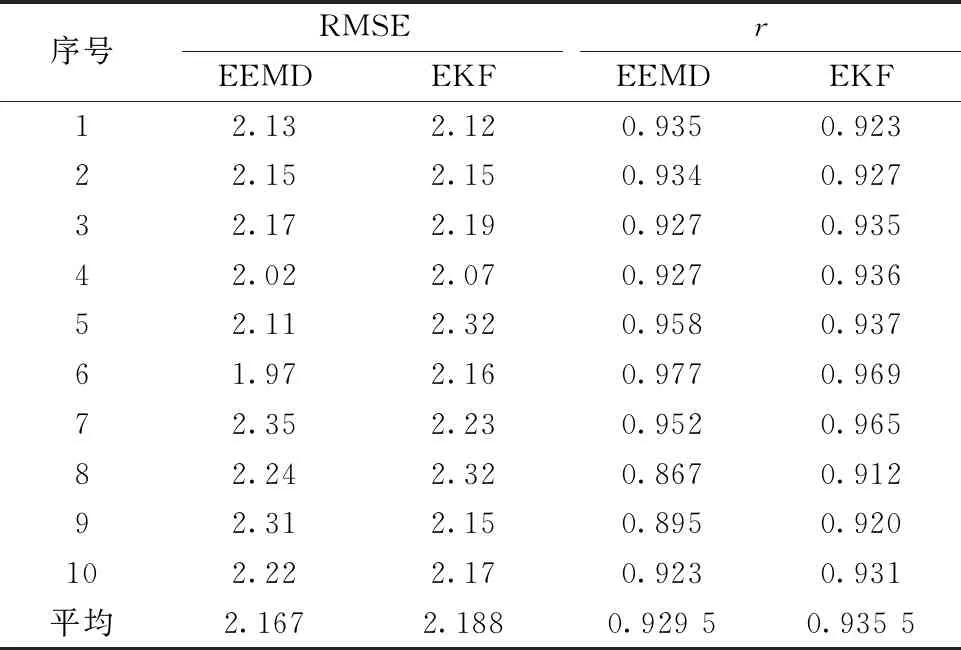
表2 EKF和EEMD算法比对
4 结 论
设计了功能性近红外光谱(fNIRS)脑血流信号采集装置, 进行了Valsava和视觉诱发实验, 采用扩展的卡尔曼滤波(EKF)建立数学模型, 对所采集信号进行了EKF处理。 通过实验表明: 本文所提出的装置和算法可以有效去除符合高斯分布的干扰, 提取出脑血流中氧合血红蛋白(HbO2)和还原血红蛋白(HbR)变化曲线图; 和主流的EEMD提取脑信号算法比对其RMSE值提高了0.96%,r值提高了0.6%。 表明本文所提出的方法有一定的优越性。 并可以为相关脑部疾病诊断如癫痫病灶定位、 抑郁研究等提供了一种有效的脑信号提取途径。

