“假设”下的多元呈现——《鸡兔同笼》教学设计（二）

【教学内容】

北师大版五年级上册第99、100页《尝试与猜测》。

【教学过程】

一、激发兴趣，导入新课

1.引入课题：同学们，你们知道这本书吗？《孙子算经》是我国古代的数学名著，里面有很多有趣的数学问题，其中有一个这样有趣的问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”你们知道这道题目是什么意思吗？今天我们就来学习有趣的“鸡兔同笼”问题。

2.导入新课：（出示图片）你能猜出笼子里有几只兔、几只鸡吗？

课件出示：笼里有鸡和兔共9只。

师：猜猜看有哪些可能？

预设1：1只鸡8只兔。

预设2：2只鸡7只兔。

预设3：3只鸡6只兔。

……

师：有这么多猜测，那怎样清晰地整理出你们说的这些可能呢？

生：用列表格的方法。

师：是的，说得真好！（课件整理出示表一）

表一：

鸡有几只 0 1 2 3 4 5 6 7 8 9兔有几只 9 8 7 6 5 4 3 2 1 0

师：你们能具体确定它们的只数吗？

生：不能！缺少条件。

师：出示题目：鸡兔同笼，有9个头，26条腿。鸡、兔各有几只？

【设计意图：从我国的数学名著导入，让学生感受我国传统的数学文化。“鸡兔同笼”问题是我们生活中经常会看到的数学趣题，让学生猜鸡和兔的数量，激发学生的学习兴趣。考虑到《孙子算经》中原题的数据较大，首先从例题中的简单问题开始研究。】

二、合作学习，探索规律

●活动一：化繁为简，探索不同解题方法。

1.理解题意：谁能说说这道题的意思？

明确：鸡兔同笼，一共9只，每只鸡有2条腿，每只兔有4条腿，笼内鸡和兔的总只数是26，分别求出鸡和兔各有几只？

2.列表法。

师：现在你能猜出鸡兔各有几只吗？怎么知道你猜测的是否正确呢？

整理表格。（每只鸡有2条腿，用鸡的只数×2=鸡的腿数，每只兔有4条腿，用兔的只数×4=兔的腿数）

表二：

鸡有几只 0 1 2 3 4 5 6 7 8 9兔有几只 9 8 7 6 5 4 3 2 1 0腿有多少条 36 34 32 30 28 26 24 22 20 18

师：表格中，我们从鸡有0只开始逐一假设列举，这种方法叫做逐一列举法。

【设计意图：由于“鸡兔同笼”原题的数据较大，不便于学生进行探究，所以以化繁为简的思想为指导，先安排一道数据较小的“鸡兔同笼”问题，一步一步引导学生猜测，让学生发现在已有的条件中，哪些条件是不变的，再让学生用自己的方法来解决，不仅吸引了学生的注意力，也激发了学生继续探究的兴趣。学生觉得用形象、清晰的列表法就能较快地解决有趣的难题。】

●活动二：回归原题，进一步探究解题方法。

出示：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？

师：通过刚才的学习，你们觉得用哪种方法比较合适？

预设：列表法。

1.提问：谁来说说这道题怎么列表？

师：大家思考一下，说说在这道题中，用这种逐一列表的方法怎么样？你有什么好的想法呢？

汇报预设：在这道题中，用逐一列举法，列举的次数较多，为了减少列举的次数，可以先估计鸡和兔数量的范围，再用列表法的方法解决问题。

2.小组讨论交流，在《作业单》上填一填。

（1）展示交流。

汇报预设：

表三（部分）：

鸡有几只 兔有几只 腿有多少条0 35 140 10 25 120 20 15 100 25 10 90 24 11 92 23 12 94……假如全部是兔，有140条腿……腿太多了，兔子数应该减少……差不多了，再调一点……腿数比94 少了，兔子数应该在10和15 之间

表四：

?

（2）说一说：这几种表格有什么不同？

（3）小结：先估计鸡和兔数量的可能范围，这样可以减少列举的次数，这种列举法叫做跳跃列举法。先假设鸡和兔的只数差不多，然后列举，在列表时再根据实际情况调整鸡和兔的数量，这样可以缩小列举的范围，这种列举法叫做折中列举法。

3.对比三种列举法。

师：这三种列举法中，哪种最简便？

【设计意图：教材呈现了“逐一列表、跳跃列表和折中列表”三个层次的列表方法。逐一列举：无遗漏、不重复；跳跃列举：减少尝试的次数；折中列举：缩小尝试的范围。三种列表，三个层次，本质都是“逼近”的思想。对于学生来说，列表不难，难就难在让学生在经历这一过程的基础上，掌握用列表解决问题的策略、感悟“逼近”等数学思想方法，并能在教师的引导下予以优化，能灵活选用合适的列表方法解决问题。】

●活动三：拓展提升，发现规律。

师：刚才我们用列表的方法，通过尝试、猜测解决了鸡兔同笼问题。其实这些都是我们先通过假设，再来验证的过程，如果鸡兔的只数很多，列表法就太费时间了，所以我们要借助表格找一找里面隐含的规律。

下面我们看看完整的表三，你发现了什么规律？

小结：在鸡和兔总只数不变的情况下，每增加1只兔，减少1只鸡，腿的总数增加2，反之，每减少1只兔，增加1只鸡，腿的总数减少2。只要按照这个步骤下去，不管头数和腿数是多少，都能解决问题。

师：完整的表三中的第一行数据是什么意思？

预设：假设笼中全是兔，有4×35=140（条）腿，与实际的94条腿相比较，多了140-94=46（条）腿。把1只鸡当成1只兔来计算，就会比实际多4-2=2（条）腿，46中有多少个2，就有多少只鸡。这样就可以求出鸡的只数。

鸡：（4×35-94）÷（4-2）=23（只）。

兔：35-23=12（只）。

师：完整的表三中的最后一行数据是什么意思？

预设：假设笼中全是鸡，有2×35=70（条）腿，比实际的94条腿相比较，少了94-70=24（条）腿，把1只兔当成1只鸡来算，就会比实际少4-2=2（条）腿，24中有多少个2，就有多少只兔。这样就可以求出兔的只数。

兔：（94-2×35）÷（4-2）=12（只）。

鸡：35-12=23（只）。

小结：通过大家的讨论，在列表法的基础上，发现了鸡和兔的腿数的关系，并采用假设都是鸡或都是兔的方法来解决问题，所以我们把这种方法叫做假设法。这种方法能化难为易，也是解答鸡兔同笼问题的一种好方法。

【设计意图：列表法能直观反映数据的变化，学生容易理解，可当数据较大时还是用假设法计算比较简便。但是假设法对于学生来说比较难以理解，所以用数形结合的方式让学生先发现表格中的规律，再从表中抽象出来，通过假设、计算的方法来解决鸡兔同笼问题，进一步提高学生的分析和解决问题的能力。】

三、灵活运用，拓展提高

师：今天我们学习了解决鸡兔同笼问题的方法，你们可以用这些方法来解决生活中的这类问题吗？

出示练习：乐乐的储蓄罐里有1角和5角的硬币共27枚，总值5.1元，1角和5角的硬币各有几枚？

（学生在书上独立完成）

汇报预测：

方法一：

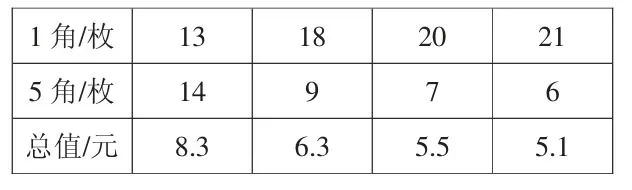
1角/枚 13 18 20 21 5角/枚 14 9 7 6总值/元 8.3 6.3 5.5 5.1

方法二：

【设计意图：通过练习，让学生在大胆的猜测、尝试和不断调整的过程中，体会出解决问题的一般策略——列表和假设法，会利用所学知识解决生活中的“鸡兔同笼”问题，让学生体会“鸡兔同笼”问题在生活中的广泛应用。】

四、全课总结

师：今天你学会了用什么方法来解决鸡兔同笼的问题？你有什么收获呢？