基于ESN的下肢表面肌电信号预测算法
熊 鸣
(北京信息科技大学 自动化学院,北京 100192)
0 引言
随着残疾人和老年人口不断增加,依靠科技创新来保障及改善他们的健康已经成为当前许多国家的战略需求。研发先进的功能康复机器人,对老年健康服务与助残公益事业具有十分重要的社会意义[1]。相比于专业康复师,康复机器人有执行效果始终保持一致的优点,缺点是无法根据训练者的实际情况更改训练计划。人的中枢神经系统中运动神经发出的动作电位通过神经纤维传导到肌肉,肌肉因此产生伸缩,肌电信号(electromyography,EMG)就是由许多微弱动作电位组合的序列总和,其中蕴涵了很多与人体动作有关联的信息[2]。如果康复机器人能够通过传感器直接获知训练者肌电信号,就可以适时地对训练计划做出改变以满足训练者要求。
Borui Li[3]设计了可穿戴下肢和踝关节EMG装置,利用EMG信号来提示使用者从坐到站的趋势,误判率和漏判率都低于5%。Jimson Ngeo等[4-5]设计了辅助运动用的外骨骼装置,通过采集健康手指的EMG信号,预测出健康手指的运动趋势以及力量,并控制辅助残肢的外骨骼,取得了较为理想的效果。Tanvir等[6]采集膝关节的EMG信号,并利用自适应神经模糊网络推理系统来估算膝盖的弯曲角度。传统的EMG信号处理都采用了神经网络来进行,需要确定神经网络的规模;而网络规模的选择只能依靠研究者的经验,数据预测结果存在着不确定性。Wang等[7]利用二进制粒子群优化方法 (binary particle swarm optimization,BPSO) 优化回声状态网络(echo state network,ESN)的输出层连接,提出了一种利用改进PSO优化ESN网络参数,并用优化后的ESN对EMG信号进行建模以及预测的方法。张杰烁等[8]用基于递归最小二乘法的回声状态网络心电信号降噪算法来消除心电信号中的复杂噪声。该算法得到含噪心电数据中非线性的且具有区分度的深层次特征,并利用这些特征自动分离心电信号与噪声。王磊等[9]提出基于灵敏度分析的模块化回声状态网络修剪算法,利用灵敏度大小判断子储备池模块的贡献度,删除灵敏度低的子模块,修剪之后的网络具有较好的泛化能力和鲁棒性。
回声状态网络[10]是一类新型回归神经网络,在混沌和非线性动态系统建模、辨识和控制等方面取得了成功应用。如在经典的Mackey-Glass(MG)混沌时间序列的前向第84步预测,其预测精度相比常见的方法提高了约2个数量级。本文采用回声状态网络来对EMG信号进行建模以及预测。
1 EMG检测装置
EMG检测装置主要由电极、检测电路和信号调理电路组成。检测下肢股二头肌EMG信号的装置如图1所示。
其中电极1与电极2分别贴在大腿肌后群股二头肌上,保持一定间距,保证两个电极在大腿做屈伸运动时,能够产生电压差。由于检测装置后端采用精密整流电路,故两个电极相对位置不影响信号输出特性。检测电路采用差分放大电路,差分放大器采用AD8221,该芯片具有高增益和高共模抑制比特性,并且增益可调。
当大腿进行屈伸运动时,所产生的差分信号经过放大器之后成为交流信号,经整流后进入滤波电路。滤波电路由工频陷波电路组成以滤除工频干扰。为了降低EMG检测装置输出阻抗,在滤波电路之后采用同向比例放大电路。
本文检测股二头肌EMG信号,故此EMG参考电位为远离大腿肌后群的股四头肌,相当于电极1和2在大腿的后部,参考电极在大腿的前部。参考电极与差分放大电路参考地线相连。电极与检测装置之间采用导联线进行连接。
2 回声状态网络
ESN由被称为储备池的内部网络与简单的输入输出网络组成,典型ESN拓扑结构如图2所示。图中左侧为M个输入节点;中间为漏积分神经元组成的储备池,由稀疏矩阵以及稀疏矩阵所对应的连接权值组成,其中稀疏矩阵为一L×L的矩阵;图中右侧为N个输出节点。其中连接输入权重矩阵记为Win,储备池稀疏矩阵记为W,输出连接权重矩阵记为Wout,输出反馈连接权重矩阵记为Wback。当ESN作为波形发生器和模式发生器时,Wback是必需的矩阵。对于本文来说,ESN作为系统建模使用,故此Wback在本文中默认为零矩阵。对ESN来说,Wout是通过训练得到的矩阵。
回声状态网络可表示为
x(t+1)=(1-α)×x(t)+α×f(Win×
u(t)+W×x(t))
(1)


(2)
通过式(2)可以得到Wout的最优估计。实际计算中,由于xTx比较容易接近奇异,将会导致Wout病态解,因此常利用岭回归的方法来替换式(2)的伪逆方法:
(3)
式中λ为正则项系数,用其作为噪声改善xTx可能的奇异性,以保证Wout有合适解。由于x初始状态为零矩阵,为了消除零矩阵初始状态的影响,参与式(3)计算中的x从n1+1时刻后开始参与计算。即[0,n1]为序列初始化,这时间段内x不参与Wout计算。ESN训练序列长度为n2,其中[0,n1]⊂[0,n2]。
3 ESN参数优化方法
3.1 参数优化目标
对于ESN来说如何获得一个好的储备池是一个至关重要的问题[10]。虽然相关研究很多,但是没有一个较为系统全面的方法。常用方法是利用训练残差来调整储备池权值,并进行相应的迭代运算以得到最优参数。源于鸟类捕食行为模拟的PSO没有变异以及交叉环节,容易陷入区域最优解。ESN参数有4个:1)谱半径ρ;2)储备池规模L;3)储备池尺度因子α;4)储备池稀疏度。储备池规模与拟合数据类型有关系,在本文中作为固定参数。储备池稀疏度调整范围较小,也作为固定参数使用。将谱半径以及尺度因子作为待优化参数,利用PSO对这两个参数所组成的二维空间进行搜索。PSO算法实质是在空间搜寻全局最优解[12],对搜索的过程和方向进行了一定约束。如果能够在搜索方向上有较为明确规定,则PSO计算量会大为减小,可以缩短优化时间。
某个信号序列ESN最优输出连接权重问题可以转化为一个约束优化问题。相对误差函数(RES)定义为
(4)
利用PSO来求解式(4)最优化问题。式(4)中所使用序列为[n3+1,n2],该序列称为测试序列,测试序列长度小于训练序列长度。
式(4)是对传统均方根误差(RMSE)的改进。RMSE定义如下:
R=
(5)
RMSE是时间序列预测等回归分析中常用的评价指标,着重点在于绝对误差,式(4)对RMSE进行了修改。相对误差越小则认为预测输出向量与期望输出向量之间欧式距离越小,两条曲线拟合度越高。
3.2 PSO粒子位置和速度的更新机制
PSO算法采用速度-位置模型[11]。PSO算法关键在于粒子位置更新,位置更新依靠更新速度。其数学描述如下。
设在一个N维解空间内,由M个粒子组成一个群组,第i个粒子位置和速度可表示为:pid=(pi1,pi2,…,pin,…,piN)和vid=(vi1,vi2,…,vin,…,viN),其中i=1,2,…,M;第i个粒子区域最优值为Pbestid=(xi1best,xi2best,…,xinbest,…,xiNbest),全局最优值为Gbestd=(x1best,x2best,…,xnbest,…,xNbest)。
粒子位置更新公式为
(6)
(7)
式中:I为总迭代次数;i为当前迭代次数;ωmax=1和ωmin=0.1分别为惯性权值的初始值和终值。
为了加快PSO优化速度,对PSO更新速度方法进行了改进,在基本PSO更新速度基础上增加一个约束条件。处理方式如式(8)所示:
pgbest2=(M+1-j)/M×pgbest+
(j-1)/M×psfbest
(8)
式中:pgbest2为当前迭代最优解位置;pgbest为RES当前迭代最优解位置;psfbest为绝对误差函数(absolute error,AE)当前迭代最优解位置;M为粒子群组的个数;j为AE最优解所对应位置在本次RES序列排序中的序号。AE定义如下:
(9)
从式(4)和式(9)可以看出,RES和AE最优解位置不可能完全相同,存在最优解不一致的可能性。假设AE和RES最优解位置相同,此时j=1,则pgbest2与pgbest相等,即当前迭代最优解位置与RES最优解位置相同。假设AE最优解位置与RES次最优解位置相同,则j=2,以此类推。式(8)对两种目标函数所得到的位置进行线性组合,以得到当前迭代最优解位置。从式(8)可以看出最优解位置还是以RES最优位置为主体,以保证ESN输出向量与期望输出向量有更好的拟合度。
由于基本PSO易陷入区域最优解,故借鉴遗传算法变异和交叉操作,对每次迭代中部分粒子位置进行变异和交叉工作。每次迭代中,对所得到的RES数值从小到大排序,对于排序中最后30%的粒子进行该操作。将最后10%的粒子群组称为A组,除去这10%之后剩下的20%的粒子群称为B组。即A与B的并集组成了排序中后30%的粒子群。A组进行变异的规则为:
1)当A组RES数值远大于B组数值;
2)当A组RES数值与B组后半部分RES数值相同时。
两个条件满足任一则进行变异。当不满足上述条件时,进行交叉操作。交叉操作对象为一个随机生成位置。本文中算法采用十进制编码方式,交叉操作为将A组粒子位置与随机生成位置进行加权平均。
B组进行交叉操作,随机生成数如果大于交叉概率0.2时,进行交叉操作。交叉操作为将B组粒子位置与当前迭代最优解位置进行加权平均。
通过对A组和B组粒子位置变异与交叉,使得在每次迭代中都有新粒子产生,极大地降低了迭代中陷入区域最优解的概率。A组变异行为类似于鲶鱼效应,给下次迭代粒子带来新位置,使得下一次迭代过程有新的激励元素。
3.3 优化步骤
本文所使用的优化目标函数是RES,故满足下面两条中任何一条即可退出优化过程:1)当A<(n2-n3)×0.052=2.5×10-3×(n2-n3)并且测试序列中有90%以上的个体相对误差小于5%;2)迭代次数到达迭代上限。
优化步骤为:1)对变量进行初始化;2)利用式(1)和式(3)得到Wout;3)得到每个粒子的优化目标函数值;4)对每个粒子RES和AE进行排序,根据式(8)更新当前迭代最优解位置;5)对RES排序中后30%的粒子位置进行变异和交叉操作;6)判断是否满足退出优化条件,不满足则从第2步开始继续优化,满足则退出优化过程。
4 实验结果与分析
4.1 实验结果
图3~6为经过归一化处理后的EMG信号,EMG信号采样频率为280 Hz,S为该采样数据序列的均方差。图3和图4为大腿做被动屈伸运动时EMG信号。大腿被动屈伸运动主要由外力引起,图3为左腿EMG信号,图4为右腿EMG信号。图5和图6为大腿进行自主屈伸时EMG信号。大腿屈伸运动是自主行为,并且该自主行为以右腿蹬踏为主,模拟肢体残障人士双腿肌力分布不均的情况。图5为左腿EMG信号,图6为右腿EMG信号。从图中可以看出左右腿EMG信号并不完全相同,主要是由于检测装置以及左右腿肌肉不同所造成。
所选用ESN稀疏矩阵为(500×500),稀疏度为4%,正则项系数 为1×10-5,待优化参数为尺度因子和稀疏矩阵谱半径,训练序列为[0,600],测试序列为[500,600],初始序列为[0,100]。PSO粒子群数量为10,粒子群速度更新上限为0.1,下限为-0.1。区域最优解学习因子以及本次迭代最优解学习因子均为2,PSO迭代次数为100。为了验证本文改进算法的预测效果,对3种算法进行比较:1)利用ESN常用的RMSE作为优化目标函数,优化采用基本PSO,PSO退出机制采用本文提出的方法(算法1)。2)利用本文提出的RES作为优化目标函数,优化采用PSO算法,其中速度-更新算法中惯性权重为经典线性递减方式如式(7)所示,PSO退出机制采用本文提出的方法(算法2)。3)利用本文提出的RES作为优化目标函数,PSO速度-位置更新办法采用本文的改进算法,退出机制采用本文提出的方法(算法3)。利用这3种算法对图3~6的数据进行预测,结果如表1~4所示,表中数据均为10次预测的平均值。

表1 图3数据的10次预测平均数值
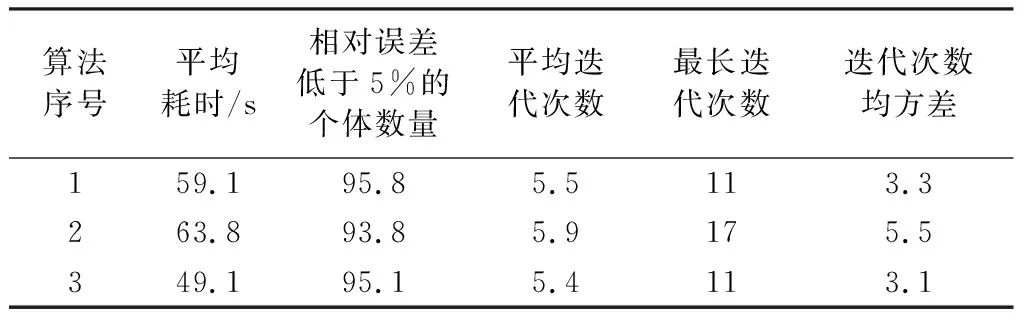
表2 图4数据的10次预测平均数值

表3 图5数据的10次预测平均数值
4.2 实验分析
从表1和表3数据对比来看,3种算法没有明显区别,在不同指标中各有优势。表2和表4数据对比说明,算法3在平均寻优速度上具有一定优势。尤其表4中算法3平均寻优时间是算法2的1/3左右。表2和表4迭代次数均方差数据说明了算法2在10次预测中优化时间分布不均衡,因此优化时间最长,这反映了基本PSO在优化时比较容易陷入局部最优的特点,同时也说明本文的改进算法能够在一定程度上避免这种缺陷。
通过数据对比可以看出,当数据序列均方差较小时,3种算法效果基本一致,当均方差较大时利用本文算法则可以较快得到符合要求的解。改进算法通过对当前全局最优解的二次处理以及对部分粒子进行变异和交叉操作之后,提高了解空间的搜索效率。本文算法在各项指标中不一定最优,但却是较快找到符合优化条件的算法,为预测的实时性奠定了基础。
5 结束语
本文在回声状态网络基础上,使用改进PSO算法对ESN参数进行优化,利用PSO找到适合于不同EMG序列的ESN参数。通过数据对比发现,ESN在时间序列预测方面具有较好的效果。本文所提出的改进PSO算法提高了ESN参数解空间的搜索效率。

