基于传热系数的高温循环流率测量方法研究

张杨鑫，王志宁，张 扬，程 璐，樊保国，张 海，吕俊复

(1.太原理工大学 电气与动力工程学院，山西 太原 030024；2.清华大学山西清洁能源研究院，山西 太原 030032； 3.清华大学 能源与动力工程系 热科学与动力工程教育部重点实验室，北京 100084)

0 引 言

循环流化床(CFB)锅炉是一项发展潜力巨大的煤清洁燃烧技术，具有燃料适应性广、燃烧效率高、低成本脱硫脱硝等优势[1-3]。在CFB锅炉中，循环物料流率Gs是表征炉内物料平衡和压力平衡的重要参数[4-5]，可以反映循环流化床锅炉炉内传热和传质、炉内温度的均匀性[6]。在CFB定态设计理论中，Gs是确定炉膛内物料流态的重要参数，而炉内物料流动状态又影响炉内的燃烧过程，进而影响污染物的生成[7-8]。因此，准确获得Gs对于循环流化床锅炉的设计和运行十分重要。

测量管道中固体流率的方法主要分为两类：① 间接式测量法，包含静电传感器[9]、数字成像技术[10]、示踪粒子[11]等方法，其精度高，不会破坏管道内气固流动，但成本高、操作环境要求高，在高温测量环境中无法正常使用；② 直接式方法，包括冲击法[12]、叶轮法[13]和振动探针法[14]等，其制造成本较低，环境适应性强。其中，冲击法流量测量装置在解决了磨损和堵塞问题的前提下，可实现实际工业CFB锅炉上的在线测量[15]。

由于CFB锅炉中物料温度超过800 ℃，Burkell等[16]针对这种高温物料，提出了一种以计量热交换量来测量Gs的方法。该方法通过在CFB锅炉料腿增设一段水冷壁，同时测量此段水冷壁进出口水温温差、冷却水流量以及经过水冷段前后高温物料平均温差的方式，利用热交换量推算循环流量。该方法能够实现800 ℃左右的高温测量，并在实验室规模的试验中得到验证。但该热交换量法应用于实际CFB锅炉中仍存在困难：① 该方法要求水冷段内无内热源，但实际CFB锅炉的料腿中常存在“后燃”现象，使该方法的条件不成立；② 实际CFB锅炉的料腿尺寸较大，使用水冷壁会破坏料腿横截面的温度均匀性，使高温物料的温度测量不具有代表性，造成较大的测量误差。

基于CFB锅炉内受热面的传热系数与固体物料浓度和运动速度等有关[17-19]，本文提出一种基于传热原理的高温物料循环流率测量方法。不同于文献[16]中直接测量换热量，本文提出的方法仅通过测量冷却水温差计算传热系数k，建立传热系数k和Gs的关联式来计算物料流率。本文的换热法使用结构简单的换热套管，通过测量物料与管壁之间传热系数k的变化得到Gs，克服了高温测量的难点，且由于冷却介质在换热装置内部不断冲刷降温，可减轻高温固体颗粒对测量装置表面的烧蚀磨损。本方法采用传热原理，无需计算整体热平衡，因此无需考虑测量段内是否有内热源的影响。本方法也无需采用水冷壁的设计，不会破坏料腿内横截面温度的均匀性，因此仅需在料腿内布置少量体积较小的换热表面测量k值，对于下降管内的气固流动影响较小，同时结合物料流动的截面分布规律，即可“以点代面”的推算出Gs。因此，该方法原理简单，且制造成本低，具有实现大型化系统测量的潜力，对于测量环境较差的应用场合，更具优势。为了适应不同温度和实际工况，本文获得了料腿中下降流换热关联式，并研究了计算关联式的通用性。研究结果将对CFB锅炉高温循环物料流率测量技术的发展提供理论指导。

1 试 验

1.1 Gs换热式测量方法原理

Gs换热式测量的基本原理如图1所示，由于循环流化床锅炉料腿内的物料流动方向是单向下行，不存在类似于提升管中复杂的返混情况，因此测量位置选定在料腿中。本文改进的换热法测量装置可分为外套管和中心管，外套管的前端伸入料腿中与高温的固体物料直接接触，中心管中通入冷却水，冷却水管路上采用流量计记录水流量，采用热电偶记录进出口水温变化，待换热过程稳定后，根据水流量和进出口水温即可得到该换热过程的换热量，炉内物料温度可从中控室采集，根据固体物料温度和冷却水的定性温度，可计算出高温颗粒和装置表面之间的传热系数k，仅需通过建立的Gs与k的关联式，即可得到Gs。

图1 Gs的换热式测量方法示意Fig.1 Schematic diagram of Gsmeasurement method using heat transfer process

1.2 热态试验系统

本文搭建的热态试验系统如图2所示，主要包括加热系统、物料分布装置、测量段、换热管、温度采集系统、计量水泵和物料计量系统。加热系统包括一台管式炉和不锈钢加热管，固体物料装在不锈钢管中加热，加热管材质为不锈钢310s，最高承受温度为900 ℃，加热管的加热部分长2.2 m，最大固体物料容量为6.5 kg，试验中采用2种粒径范围的固体物料——石英砂，其物理性质见表1。

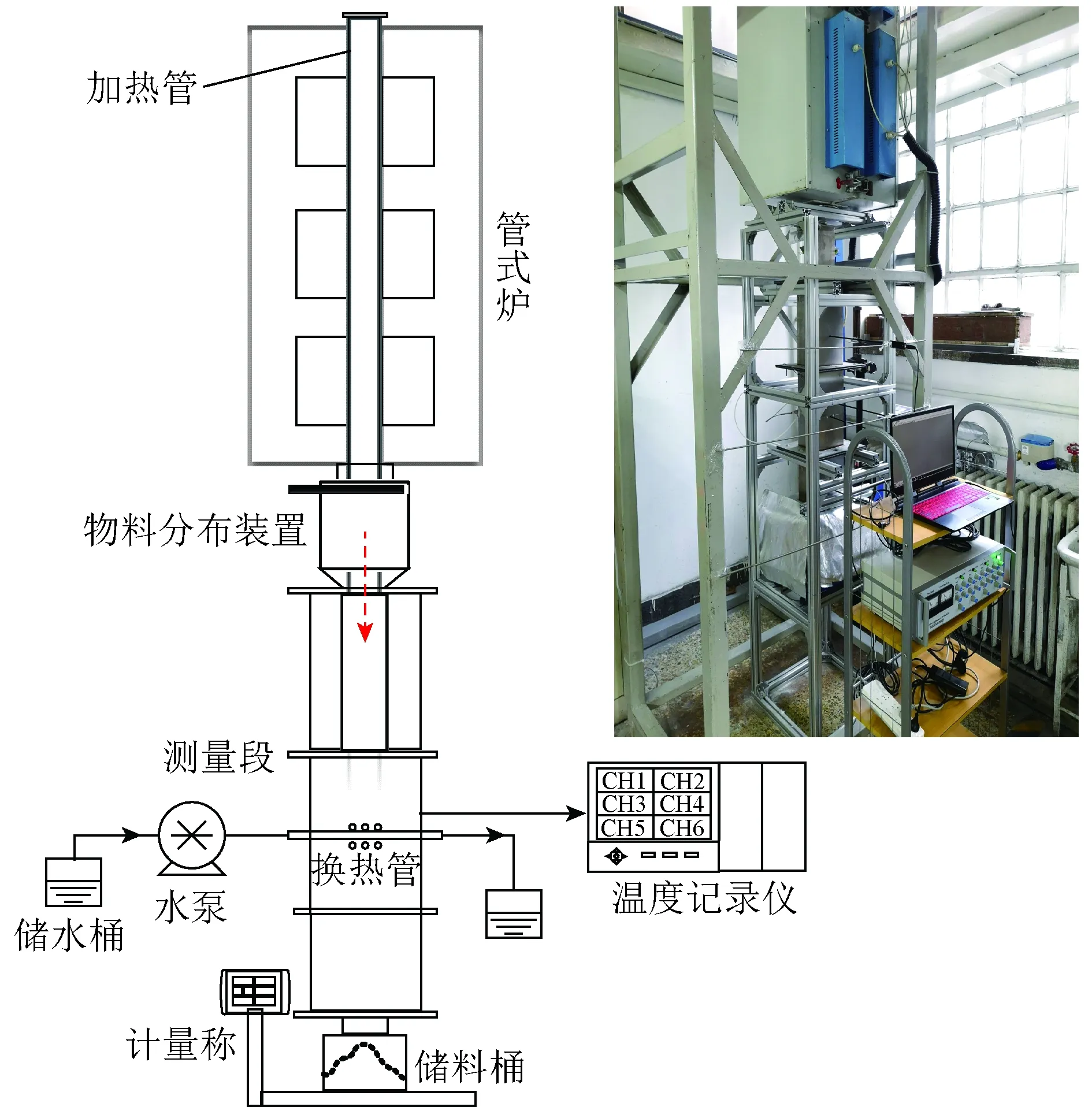
图2 热态试验系统Fig.2 Thermal experimental apparatus

表1 石英砂物性参数

物料分布装置用于改变试验中的物料流率，在水平和侧面方向上分别设有一块可活动的水平挡板和2块侧挡板，通过控制侧挡板位置形成不同的开度，装置的底部设计为缩口，确保物料能够顺利进入测量段中，图2中虚线箭头方向为物料下落路径。在测量段上方设有物料的分布装置，让物料下落时横截面分布均匀。

测量段整体分为中心的方管和保温外壳，两层之间填充保温棉，防止高温固体颗粒热量散失，内部方管的横截面积为(0.04×0.06) m2，侧面中心位置处开贯通的小孔放置换热管。换热管尺寸为总长20 cm，外径4 mm，壁厚0.2 mm，与高温物料接触的换热段为方管内6 cm段，换热管材质为紫铜，导热系数为400 W/(m·K)。温度采集系统中Pt100热电阻测量进出口水温，铠装K型热电偶测量颗粒温度，热电阻的精度为A级，热电偶的精度为Ⅰ级，响应时间均小于0.2 s，温度数据由MIK-9600智能温度记录仪采集，采集通道数为18，采集频率为1 s。物料计量系统由小型电子秤和不锈钢储料桶组成，计量秤可记录物料下落的质量变化，储料桶承接落下的高温物料。

试验中将石英砂加入到加热管中，水平抽板保持关闭状态，通过调整侧面挡板形成不同的开度，对应不同的物料流率。打开管式炉，按照目标温度设置升温程序，一般以5 ℃/min的速率升温，升温程序结束后继续在设定温度下加热一段时间，确保颗粒温度达到设置温度。加热完成后，打开计量水泵，设定水流量，水流量稳定后，打开水平抽板使高温颗粒落下，当颗粒冲刷过换热管时，出口水温开始迅速变化，温度记录仪采集颗粒温度和进出口水温，颗粒下落后全部进入储料桶中，根据颗粒下落期间的质量变化，物料实际流率为下落物料质量随时间变化的斜率和方管横截面积的比值。

根据试验温度数据和水流量可计算传热系数(式(1))。由于换热管的导热系数很大，且壁厚仅0.2 mm，经计算，管外的传热系数与管内相差2个数量级以上，因此在本文试验条件下，由式(1)计算的传热系数即为高温颗粒与换热管表面之间的传热系数。

(1)

式中，qm为冷却水流量，kg/s；Cp,w为水的比热容，J/(kg·K)；tout为出口水温，℃；tin为进口水温，℃；A为颗粒与换热管接触面积，m2；ts为石英砂颗粒温度，℃；tf为冷却水的定性温度，tf=(tin+tout)/2，℃。

2 试验结果与讨论

试验颗粒温度分别设置为300、400、600 和800 ℃，颗粒流率为20～90 kg/(m2·s)，2种颗粒平均粒径分别为171、339 μm。试验出口水温变化为初始数据，所有工况中，虽然出口水温的绝对数值变化较大，但变化规律类似，因此只选取400 ℃部分工况的出口水温变化进行分析。图3为颗粒温度400 ℃时3种不同Gs下出口水温变化。高温颗粒开始接触换热管表面时，换热管出口水温迅速升高，表明高温物料与换热管表面发生强烈的换热，冷却水吸收热量后，温度迅速上升，当出口水温升高到某一定值后基本不再变化，表明换热过程达到相对稳定的状态，可认为冷却水与高温颗粒之间达到了稳态，颗粒完全落下后，出口水温下降。计算传热系数时，仅需对达到稳态的数据进行分析。

图3 出口水温的变化Fig.3 Variations of outlet water temperature

对稳态段的数据进行计算后，可得到一组瞬态传热系数值，需要对数据进行粗大误差剔除和误差分析。式(1)敏感性分析如图4所示，可见进出口水温的测量是对k测量结果影响较大的2个参数。由于进口水温不变，主要基于格拉布斯准则，对出口水温和颗粒温度进行粗大误差剔除，剔除后颗粒温度和出口水温最大偏差分别为3.31 ℃和2.24 ℃，换算百分比为3%和4%。

图4 敏感性分析Fig.4 Sensitivity analysis

利用误差分布原理对传热系数k进行误差计算，即

(2)

其中，σk为传热系数k的标准偏差；σs、σout、σin分别为颗粒温度ts、出口水温tout、进口水温tin的标准偏差。计算结果表明，所有计算的瞬态k值最大标准误差不超过±20%。取每组工况瞬态传热系数的平均值作为该组工况对应的传热系数进行分析。

2.1 颗粒流率对传热系数的影响

为了研究颗粒流率与传热系数之间的关系，在同一颗粒温度和颗粒粒径工况下，颗粒温度400 ℃时平均传热系数与物料流率之间的关系如图5所示。可以看出，当颗粒温度和颗粒粒径一定时，随Gs增大，k增大，二者呈正相关关系。

图5 传热系数k随颗粒流率的变化Fig.5 Variation of k with particle flow rate

k增大的主要原因是由于Gs的增大造成测量段截面上颗粒浓度增大，在颗粒下落过程中高温颗粒与换热管表面的碰撞几率增加，高温颗粒和换热壁面的换热过程更加强烈，从而使颗粒与换热管表面之间的k增大。

2.2 颗粒温度对传热系数的影响

颗粒粒径相同，300、400、600 ℃下温度对传热系数的影响规律如图6所示。可以看出，在颗粒流率和颗粒粒径相同时，传热系数随颗粒温度的升高而增大。对比300 ℃和400 ℃的传热系数平均值，二者相差近一倍，表明温度与传热系数呈正相关关系，且随温度的升高，传热系数显著增大。400 ℃和600 ℃时，传热系数数值增大幅度不大，其原因可能是在600 ℃时颗粒下落的速度比对应流率下400 ℃时的速度大，虽然温度高使传热系数增大，但是由于颗粒速度大，换热管表面的颗粒更新快，停留时间减少，导致换热强度减小，因此传热系数增加幅度不大。

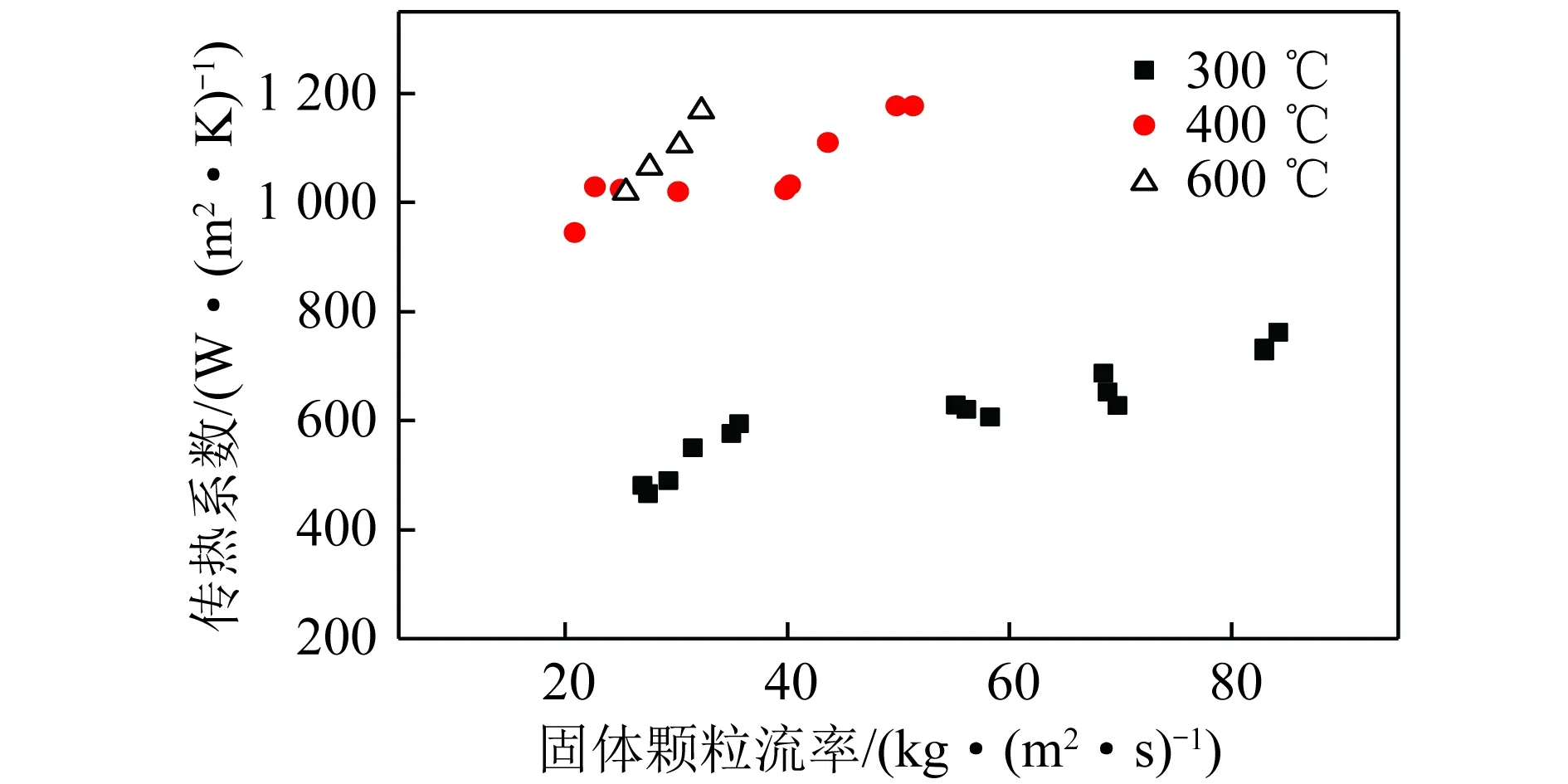
图6 传热系数k随颗粒温度的变化Fig.6 Variation of k with particle temperature

2.3 颗粒粒径对传热系数的影响

为了探究高温条件下颗粒粒径对传热系数的影响，800 ℃下改变物料粒径，选用d50=339 μm的颗粒进行试验。图7为在600、800 ℃时2种不同粒径颗粒的传热系数变化。虽然颗粒温度从600 ℃升至800 ℃，且800 ℃的流率更大，但800 ℃的传热系数小于600 ℃。小粒径颗粒在600 ℃下的传热系数最大数值可达103左右，而大粒径颗粒的传热系数较之减小了近50%，表明颗粒粒径与传热系数呈负相关，随着颗粒粒径增大，传热系数减小。其主要原因可能是由于大颗粒与换热管表面的接触面积较小，且颗粒粒径增大导致颗粒速度增大，颗粒在管壁的停留时间减少，换热强度减弱，使传热系数减小。

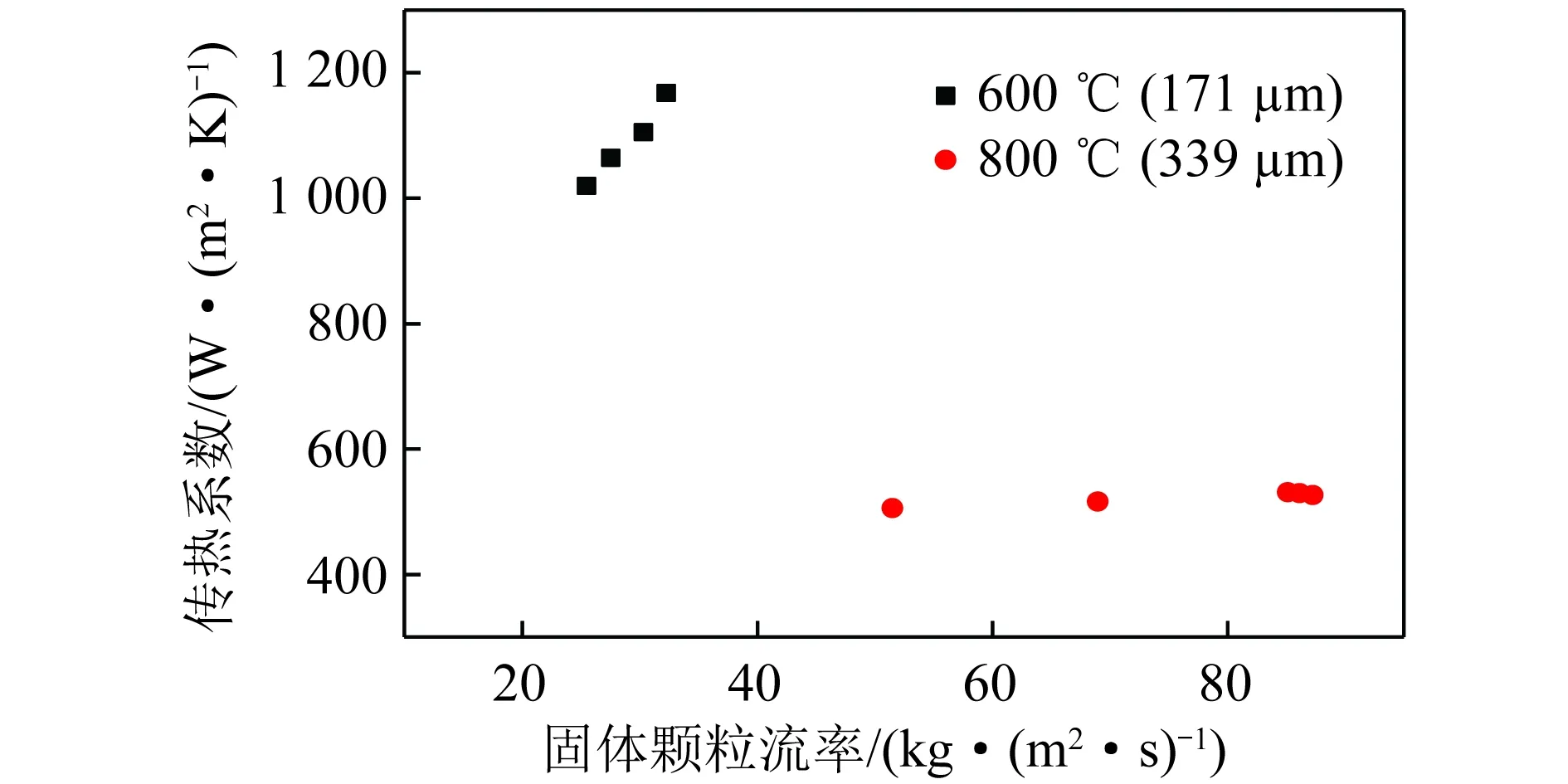
图7 传热系数k随颗粒粒径的变化Fig.7 Variation of k with particle size

2.4 颗粒流外掠圆管对流换热特征数方程

根据上述分析，可认为颗粒流与换热管表面之间的传热系数与颗粒流率、颗粒温度、颗粒粒径等有关，且颗粒速度影响颗粒浓度和停留时间，从而影响传热系数。由于传热系数的影响因素较多，且不同温度下，颗粒流率与物料流率之间的函数关系无法统一形式，因此采用特征数方程表示，并找出传热系数和物料流率之间的关系。根据文献[19-20]以及热态试验的测量数据可知，将各影响因素归纳为颗粒流的无量纲参数中：如阿基米德数Ar、努塞尔数Nu、雷诺数Re和普朗特数Pr组成的关系式。

Borodulya等[20]提出了一种在试验条件下具有较高精度的预测传热系数经验关联式，即

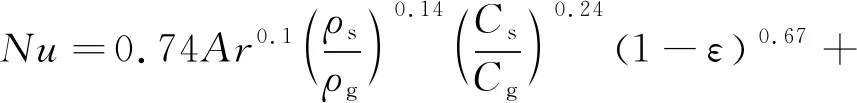
(3)

式中，ρs为固体颗粒密度，kg/m3；ρg为气体密度，kg/m3；Cs为固体颗粒的比热，J/(kg·K)；Cg为气体的比热，J/(kg·K)；ε为空隙率，计算公式为

(4)

式中，φ为颗粒体积分数；u为通道来流速度，m/s。

阿基米德数Ar为

(5)

式中，dp为颗粒粒径，m；g为重力加速度，m/s2；μg为气体黏度，Pa·s。

努塞尔数Nu为

(6)

式中，λg为气体导热系数，W/(m·K)。

颗粒流的雷诺数Re为

(7)

颗粒流的普朗特数Pr为

(8)

图8为模型预测值和试验值对比，可以看出，试验值都在模型预测值的±25%内，可以认为模型式(3)能够较好地预测热态条件下的传热系数，模型适用条件为：0.1 mm≤dp≤6.0 mm、0.1 MPa≤p(压力)≤10.0 MPa、20 ℃≤ts≤1 440 ℃。

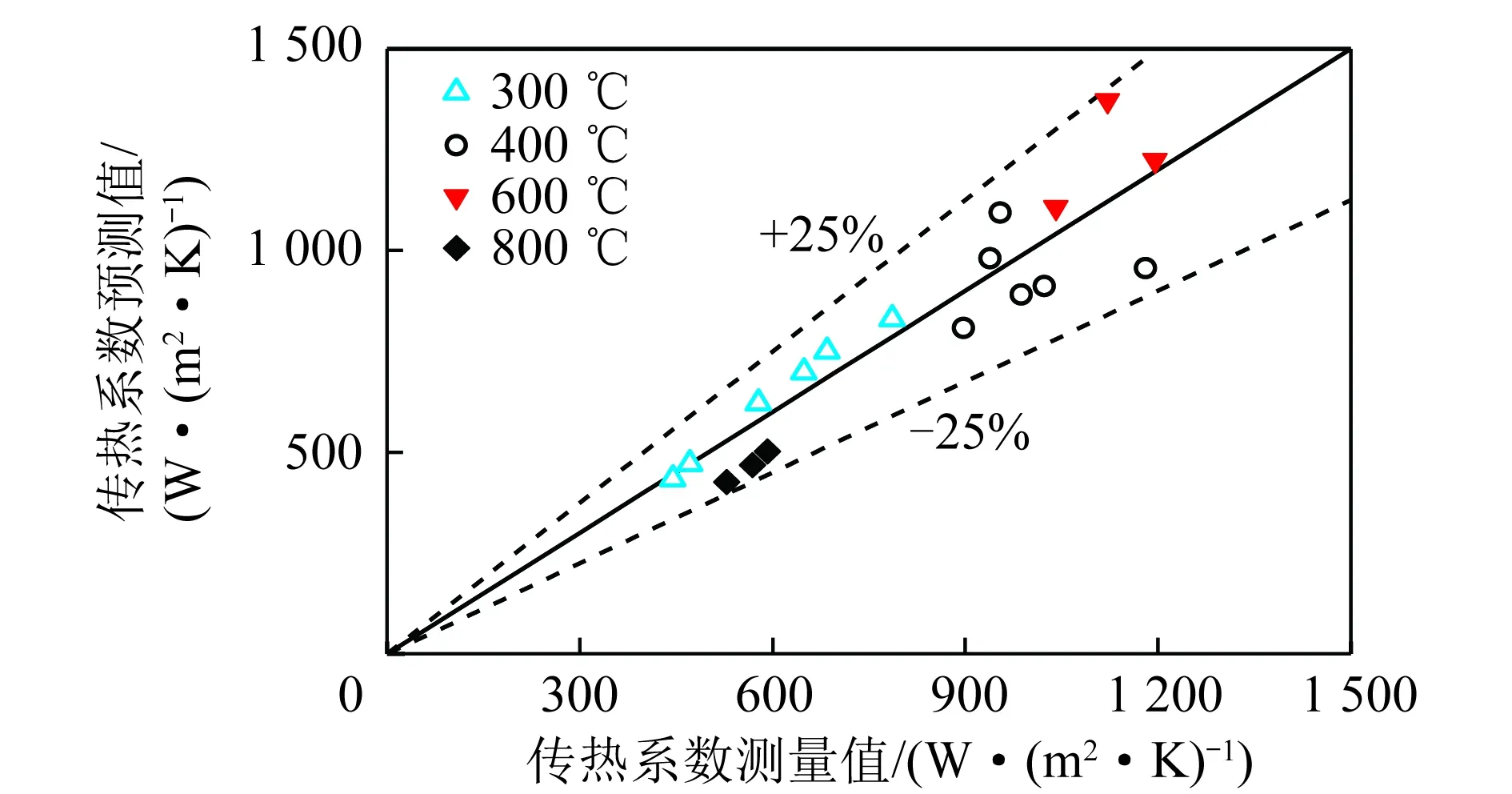
图8 传热系数k预测值与测量值比较Fig.8 Comparison between the predicted values and the measured values of k

将式(4)代入(3)可得到传热系数k与物料流率Gs之间的关联式，即

(9)

根据式(9)，选取实际料腿中的Gs变化范围和灰渣参数进行传热系数计算。料腿中Gs在100～1 000 kg/(m2·s)时，传热系数的计算值如图9所示。可以看出，随着Gs增大，传热系数k单调增大，说明通过计算模型得到的传热系数k和Gs之间可一一对应，本文改进的换热法原理适用于测量Gs，不存在多解的情况。

本文得到的换热法计算公式对传热系数的测量值进行计算，得到对应的颗粒流率值，并与设定的颗粒流率进行对比，结果如图10所示。式(9)计算得到的流率值在±25%范围内可以预测颗粒流率Gs试验值，说明该计算模型可较准确地测量颗粒流率Gs。

但温度较高时(>800 ℃)，辐射和对流换热对整体传热起重要作用。式(1)中的k为总传热系数，当辐射传热占比较高时，式(3)～(9)需辐射修正。

在实际流化床下降管内，管道内的速度并非均匀分布。因此，后续需要进一步获得截面物料分布规律，在特征点布置测点，从而推断出截面平均Gs值。

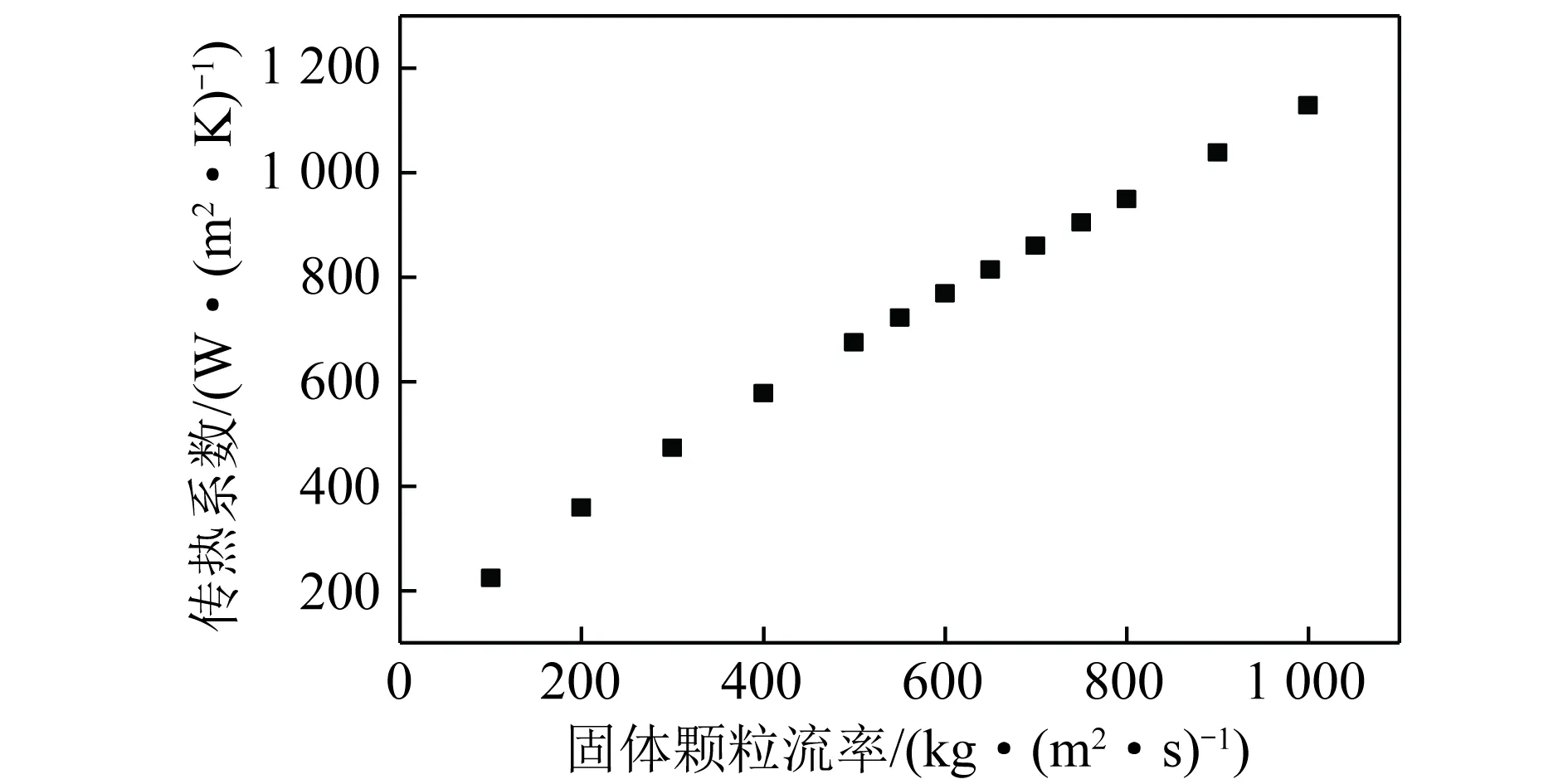
图9 传热系数k随Gs的变化Fig.9 Variation of k with Gs

图10 设定流率值与换热法测量得到流率值比较Fig.10 Comparison between the pre-set values and the measured values using the heat transfer method

3 结 论

1)高温物料和管壁之间传热系数k的影响因素主要有颗粒流率、颗粒温度、颗粒粒径等，主要表现为颗粒温度和颗粒粒径一定时，随着颗粒流率增加，k增大；颗粒流率和颗粒粒径相同时，k随着温度的升高显著增大；颗粒粒径与k呈负相关关系，当大粒径物料温度和流率均高于小粒径物料时，大粒径物料的k显著减小。

2)本文推导出颗粒流外掠圆管对流换热的计算模型，其中包含颗粒流率、颗粒粒径、颗粒流速度等参数，可更好地预测传热系数。热态试验测量值可完全落入计算模型预测值的±25%以内，模型中Nu与Re和Pr呈正相关关系，模型的适用条件为0.1 mm≤dp≤6.0 mm、0.1 MPa≤p≤10.0 MPa、20 ℃≤ts≤1 440 ℃，可满足常压、高温工况下传热系数的预测。

3)建立了传热系数k和循环物料流率Gs之间具有通用性的关联式，确保Gs和k之间存在单调对应关系，且关联式在±25%范围内可以对实际的Gs进行较好地预测。本文研究结果改进和完善了换热式测量方法，为后续换热式流量计的样机在实际大型锅炉中的应用提供了新的研究方向和思路。