基于形状分布式模型检索的农机装备快速设计方法
刘洪豪 张开兴,2 卢 山 刘贤喜,3
(1.山东农业大学机械与电子工程学院,泰安271018;2.山东省农业装备智能化工程实验室,泰安271018;3.山东省园艺机械与装备重点实验室,泰安271018)
0 引言
模型检索是一种重要的设计重用方法[1],可有效促进机械装备实现快速化设计。现阶段基于三维模型的产品设计与制造已成为我国制造业主流模式[2],研究表明,包括农业机械领域在内的三维模型数量每年以指数方式增长[3]。面对数量与日俱增、种类日新月异的三维模型,快速有效提取模型特征、并实现三维模型相似性检索已成为制约设计重用技术[4]的关键。三维模型检索方法可分为:形态特征统计法、视图投影法以及函数变换法,3 类方法侧重点不同,但均不同程度提高了三维模型检索效果。面向工程应用的模型检索方法需尽可能稳定、高效,其中形状分布法能够集鲁棒性、简单易用性于一体,是一种通用、高效的模型检索算法。
形状分布算法本质上是一种概率统计方法[5],该方法以特征点之间距离、角度、面积等特征为样本,经过概率统计分析,最终以特征频率分布直方图作为模型的特征表示形式。ANKERST 等[6]提出了一种基于形状直方图特征的空间模型分类方法;OSADA 等[7]成功将5 种形状分布函数应用于三维模型特征提取;LIN 等[8]对D1、D2、D3 等形状分布函数的分辨率、不变性、鲁棒性进行了多元化测试评估;模型表面采样点的均匀性影响三维模型特征提取效果,基于此SHIH 等[9]提出一种GD2 形状分布算法,该方法将三维模型体素化分解,使用体素单元替代随机采样点,提高了分布函数的分辨能力;张开兴等[10]提出了一种基于距离-夹角的形状分布算法,实验证明该方法的特征代表性优于传统形状分布算法。形状分布算法无需对三维模型进行旋转归一化处理,具有刚体变换与反射变换不变性[11]。
三维CAD 模型形态结构逐渐复杂多样,单一形式的形状特征无法综合反映三维模型主要特征。此外,传统的形状分布法生成特征点概率与模型表面网格面积存在不对称性,即网格面积越大,生成特征点概率越高,但三维模型结构形态变化主要由小面积网格表示,因此传统特征点采样无法反映模型细节特征。本文对形状分布算法的特征点采样规则以及多特征融合方式进行改进,提出一种自适应动态加权的形状分布模型检索算法,以促进机械装备三维模型检索与设计重用。
1 形状分布特征提取原理
形状分布函数本质上是一个概率分布函数,以形状特征分布作为三维模型的特征描述符,可以将复杂的三维模型间相似性度量问题转换为概率分布匹配。理论上,任何有关三维模型的特征函数均可通过样本采样形成特征描述符,例如:模型表面纹理特征、表面随机点间距离、颜色特征、材质属性等。在三维模型特征函数中,通过形状特征函数提取的模型特征描述符最为有效,图1 为常用的6 种形状分布函数,表1 为对应形状分布函数的属性特征。

图1 常用形状分布函数特征示意图Fig.1 Illustrations of frequently used shape distribution feature

表1 形状分布函数属性Tab.1 Property of shape distribution function
对于三维模型,位置方向变动引起的特征提取偏差是影响三维模型相似性匹配的主要因素,且在三维模型归一化变换过程中,旋转归一化处理最为复杂。图1 所示6 种形状分布均通过采样点间特征函数计算获得,6 种形状特征提取描述符均具有旋转不变性,其中角度A3 形状分布函数不仅具有旋转不变性,而且尺度不变,特征提取效果不受三维模型缩放、旋转的影响。此外,形状分布法是一种通用模型特征提取方法,适用于任何由三角网格表示的三维模型,非三角网格模型经过转换后同样适用。
2 动态加权融合形状分布特征
2.1 组合式特征点采样
现阶段模型表面特征点采样概率多与网格面积相关,而三维模型的特征细节主要是由一系列微小网格表示,模型特征与特征采样概率间不对称性降低了特征提取的区分度,因此使用组合分类排序法对特征点采样方式进行改进。
(1)模型预处理
设三维模型经过三角网格化后顶点集合为V={v1,v2,…,vn},其中vi=(xi,yi,zi)为网格顶点,则三维模型中心点为

式中 n——模型顶点总数量
将模型中心点平移至坐标原点,完成平移归一化,计算模型中各顶点到中心点的最大距离,采用最大半径缩放法[12],对三维模型进行尺度归一化处理
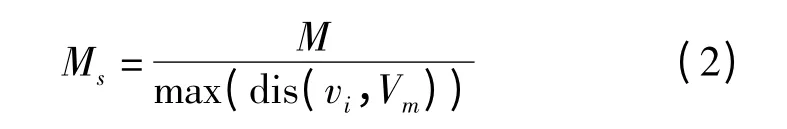
式中 M——归一化前模型
Ms——归一化后模型
dis(vi,Vm)——顶点vi与中心点Vm之间的欧氏距离
由于形状分布算法具有旋转不变性,三维模型无需复杂的旋转变换处理,在预处理过程中三维模型顶点集合均以矩阵形式存储。
(2)网格分类组合
图2 为驱动桥万向节模型网格分类组合过程,首先遍历模型全部网格顶点,根据Heron 公式计算网格面积,设三角网格顶点为(vi,vj,vk),则其面积计算公式为
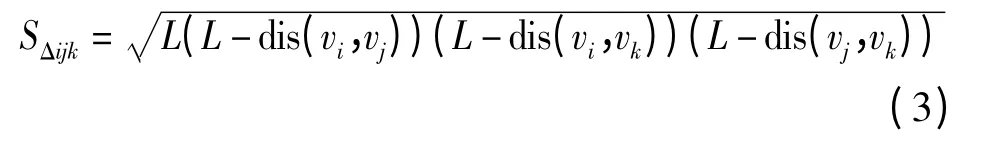
其中
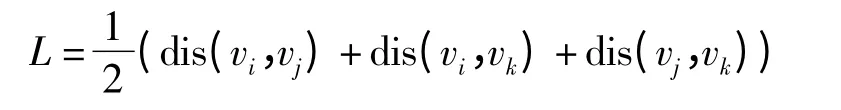
式中 L——三角网格周长一半
SΔijk——三角网格面积
然后存储网格面积及位置信息,根据面积对全部三角网格排序,对于排序后的网格有两种分类方法:网格数量分类与面积分类。模型典型细节特征由一系列面积较小的三角网格表示,数量分类法无法体现网格面积区分度,因此根据面积分类法将三角网格分为Max(Ⅰ类)、Mid(Ⅱ类)、Min(Ⅲ类)。
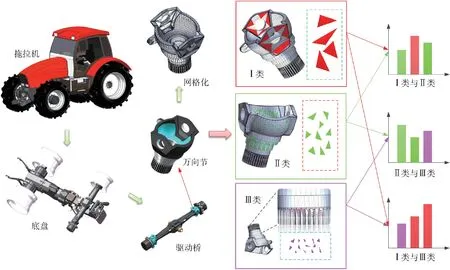
图2 模型三角网格分类与组合Fig.2 Classification and combination of model triangular mesh
网格分类后,不同类别依次交叉组合取点,计算网格表面采样点间形状特征。由于不同类别间网格位置及面积差异性增大,从而提高了模型提取特征的分辨力与区分度。
(3)准随机序列
生成随机点是完成网格采样的关键步骤,计算机无法产生绝对均匀分布的随机数,传统的伪随机数序列均匀性较差,而准随机序列分布更加均匀,常用的准随机性序列包括Halton 序列、Sobol 序列、Latin 超立方序列等[13],其中Sobol 序列具有较好的计算精度与计算效率[14],因此采用Sobol 准随机序列对分类后的三角网格采样。
Sobol 序列主要由一组方向数vt构成,其中vt=mt/2t,构造步骤如下[15]:首先,生成系数c 为0 或1的原始多项式
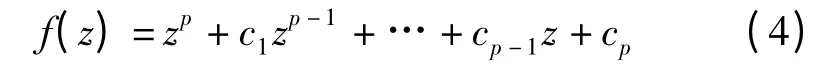
然后根据递推公式计算
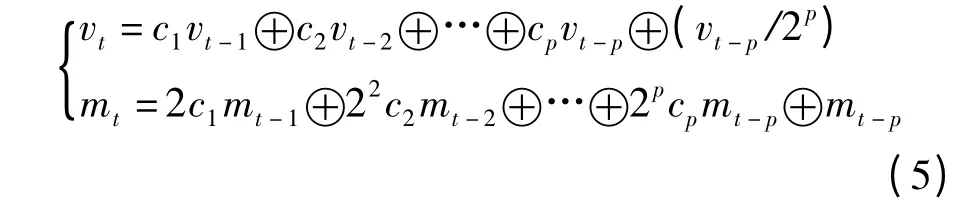
式中,t >p,mt为小于2t的正奇数,⊕表示二进制按位异或运算。
对于任何一个十进制整数y,能够唯一表示为与数基b=2 有关的表达式

式中,aj系数为0 或1,k 为大于等于lby 的最小整数。
Sobol 序列的第z 个元素可表示为

图3 为Matlab 中伪随机序列与Sobol 准随机序列二维分布,准随机序列分布更加均匀。
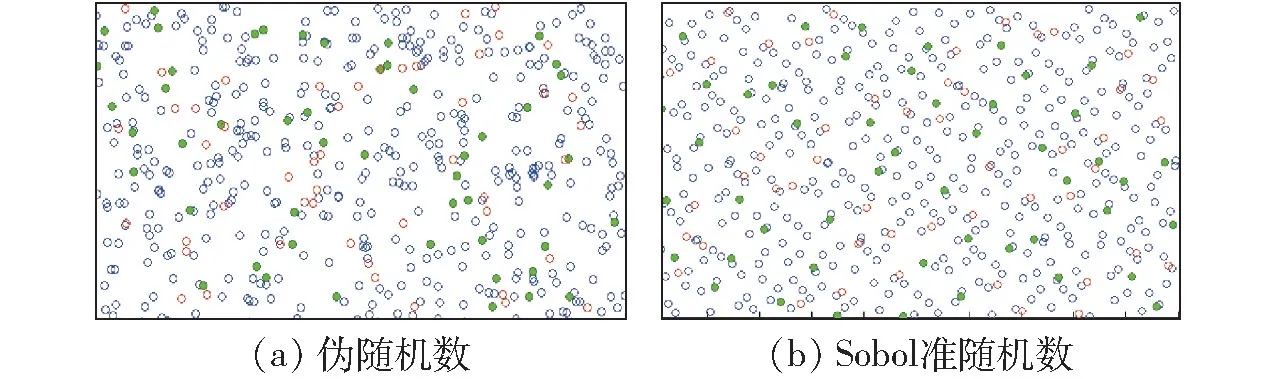
图3 随机序列数二维分布Fig.3 Distributions of random sequences
根据准随机序列选定不同类别集合中三角网格,以三角网格重心为采样点,完成模型特征点采样。
2.2 自适应特征融合
特征融合可有效弥补单一特征代表性不足的缺点,现阶段的形状分布算法种类多样、功能专一、效率不同,对典型形状分布特征进行有机融合,不同形状分布特征优势互补,从而提高模型特征代表性与区分度。
(1)形状分布函数融合
特征融合需尽可能融合多种类别形状特征,但同时兼顾效率因素。由表1 可知,单个D3、A3、C1形状特征样本需要3 个采样点,D2 特征与D1 特征同为距离特征且均需要2 个采样点,体积特征D4需要4 个采样点。此外,形状特征采样具有向下兼容性,即高频采样可满足低频采样特征提取需求,因此,3 采样点作为采样基本单位的特征提取效率最高。图4 为单位采样点数为3 的融合采样特征,本文对距离D2、面积D3、曲率C1、角度A3 形状特征进行融合,实现三维模型线与面、内部与表面、距离与曲率综合特征提取。
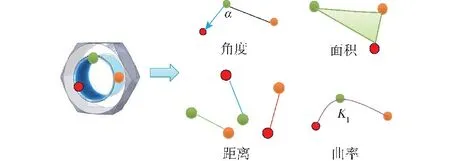
图4 融合特征采样Fig.4 Fusion feature sample
(2)自适应动态加权
对于不同类型的三维模型,每种形状分布函数的表现能力不同,为最大限度突出模型主形状特征并体现次要特征,需计算不同形状函数权重。常用的加权方法可分为固定权值法与动态加权法[16],动态加权法更适合数值波动较大的变量,本文基于变异系数采用动态加权法确定形状函数权重。
变异系数可以度量变量的离散程度[17],在评价模型融合特征体系中,特征变量幅值变化范围越大,越能反映模型主特征,因此变异系数能够度量不同特征变量权重,其计算式为

式中 Vj——第j 项特征的变异系数
xi——j 特征的第i 个样本值
Xj——j 特征的样本均值
s——样本总数
特征权重为

式中 Wj——第j 项特征权重
m——融合特征总数
将各形状分布特征变量值归一化,然后根据各形状特征权重,按照D2、D3、C1、A3 顺序将不同特征变量拼接成具有多特征的形状分布直方图,从而完成自适应加权融合特征(Adaptive weighted shape distribution,AWSD)提取。
(3)相似性度量
为实现模型库中不同模型相似性检索,需要根据形状分布直方图计算模型间相似性。距离比较是度量模型相似性的典型方法,主要包括Euclidean 距离、Manhattan 距离、Hausdorff 距离等[18],本文采用χ2距离[19],计算式为
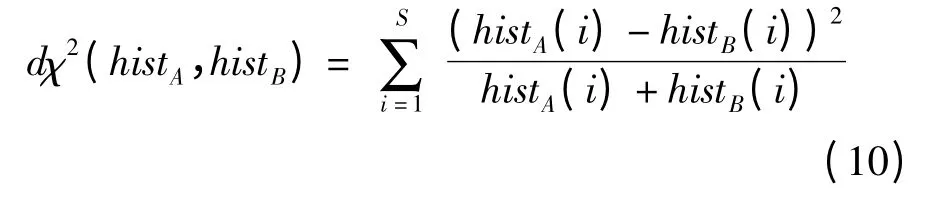
式中 histA、histB——模型MA和MB直方图
histA(i)、histB(i)——直方图第i 个特征分量频次
S——直方图特征分量总数
三维模型相似度计算式为
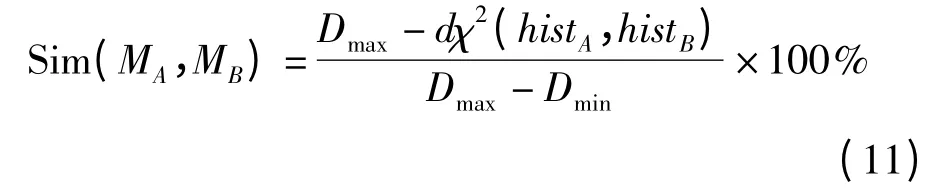
式中 Dmax、Dmin——模型MA与所有参与比较的模
型间距离最大值、最小值
3 实验与讨论
3.1 实验数据集
选用ESB 模型库[20]与农业机械装备CAD 模型库作为三维模型实验数据集,其中ESB 数据集由美国普渡大学设计开发,包括薄壁、棱柱、回转体3 大类共计867 个模型;农机模型库根据国家重点研发计划项目“农机装备智能化设计技术研究”构建,主要以联合收获机与拖拉机CAD 模型为主,共包含9大类、23 小类共计2 166 个模型,部分三维模型如图5 所示。

图5 三维模型库节选Fig.5 Part of 3D model database
3.2 评价标准
采用国际通用标准对模型检索效果进行评价,主要包括6 类指标:
(1)查准率(Precision)与查全率(Recall)计算式为
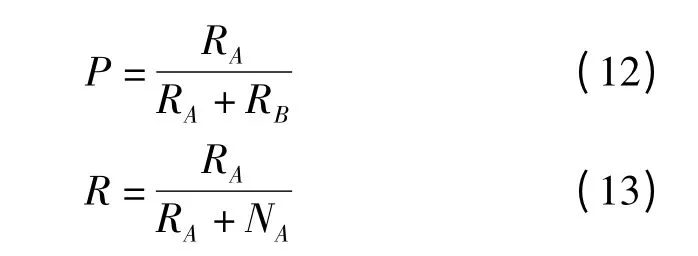
式中 RA——检索返回结果中与待检索模型相关的模型数量
RB——与待检索模型无关的模型数量
NA——整个模型库中与待检索模型相关但未检索到的模型数量
(2)E 测度计算式为
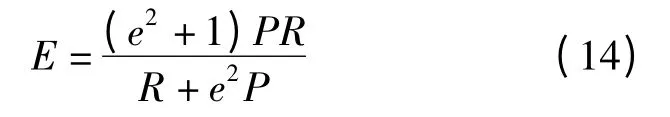
式中 e——查准率P 与查全率R 相关程度,通常取0.5 或1
(3)平均查准率(MAP)计算式为
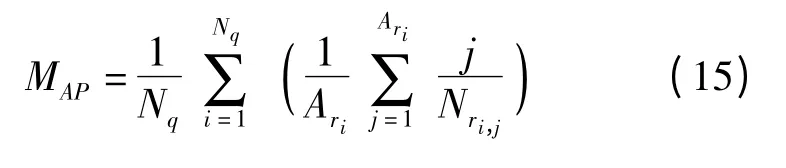
式中 Nq——待检索模型数量总和
Ari——第i 个检索返回结果中正确相关模型数量
Nri,j——返回结果中截至前j 个相关模型出现时模型数量
(4)最近邻精度(NN)计算式为

式中 N——检索精度参数,即检索返回N 项数量
Rn——返回前N 项中正确相关模型数量,通常采用第一最近邻精度(N=1)指标
(5)FT 与ST 测度
模型库中与待检索模型同类模型数量为C,则FT 与ST 分别为前C -1、2(C -1)个检索结果的查全率。
(6)排序累积增益(DCG)计算式为
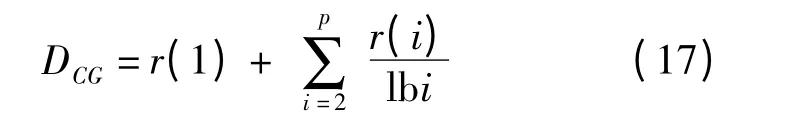
式中 p——检索返回模型总量
r(i)——第i 个模型的相关性评分
3.3 结果与分析
实验设备配置环境为Windows 10 操作系统,处理器Intel Core i7-6500U(2.5 GHz),内存8.0 GB,以VS2010 与Matlab 2016b 为开发环境,以Open Cascade 为几何造型平台。表2 为部分典型模型的特征提取结果,由表2 可知,圆盘耙模型距离D2 频率先增大后减小,拨禾轮模型距离D2 频率增大后保持,到达峰值后陡然减小,D2 形状特征随模型形状差异而变化,基本能够反映模型主要特征。表2中发动机模型与圆盘耙模型在几何形态方面显著不同,而发动机距离D2 频率特征与圆盘耙特征相似,这主要因为发动机模型较为复杂,距离D2 特征趋于正态分布,从而降低了特征的区分度与代表性[21],由此表明单一形状分布特征的区分度有限。

表2 模型特征分布图Tab.2 Model charateristic distribution
表2 同时显示了本文提出的AWSD 融合特征,其中圆盘耙模型融合特征权重为0.25、0.23、0.33、0.19,拨禾轮模型权重为0.28、0.21、0.28、0.23,发动机模型特征权重则为0.23、0.19、0.23、0.35。圆盘耙与发动机模型的D2 特征相似,AWSD 特征具有明显差异,其主要体现在形状特征波峰与波谷变化趋势以及峰值大小上,圆盘耙模型在第3 个波峰时取最大值,拨禾轮模型的4 个波峰值近似,而发动机模型特征最大值体现在第4 个波峰上。融合特征最大峰值即各组成特征最大权重,而特征权重由模型各特征差异性决定,通过自适应加权方式,AWSD融合特征能够有效弱化低区分度特征,突出模型特征差异性,提高模型特征分辨率。
为确定不同形状特征提取方法应用效果,选取拖拉机转向器、变速箱、轮胎3 类,玉米联合收获机摘穗辊、押送器2 类进行检索实验,以5 类模型平均查全率为X 轴、以平均查准率为Y 轴,绘制查准率-查全率曲线如图6 所示。理想的查准率-查全率曲线是纵坐标为1 的水平直线,实际以查准率-查全率曲线与X-Y 轴包围面积即查准率-查全率指数作为检索效果评价依据,查准率-查全率指数数值与检索效果正相关。由图6 可知,特征检索查准率由大到小依次为D2、C1、A3、D3 特征,本文提出的AWSD融合算法在查全率为0 ~0.5 区间内显著优于D2特征,在0.5 ~1.0 区间内检索效果与D2 特征近似。表3 进一步显示了不同方法的检索评价参数,AWSD特征各项指标优于其他形状分布算法,综合检索精度较D2 形状分布算法提高了8.5%。
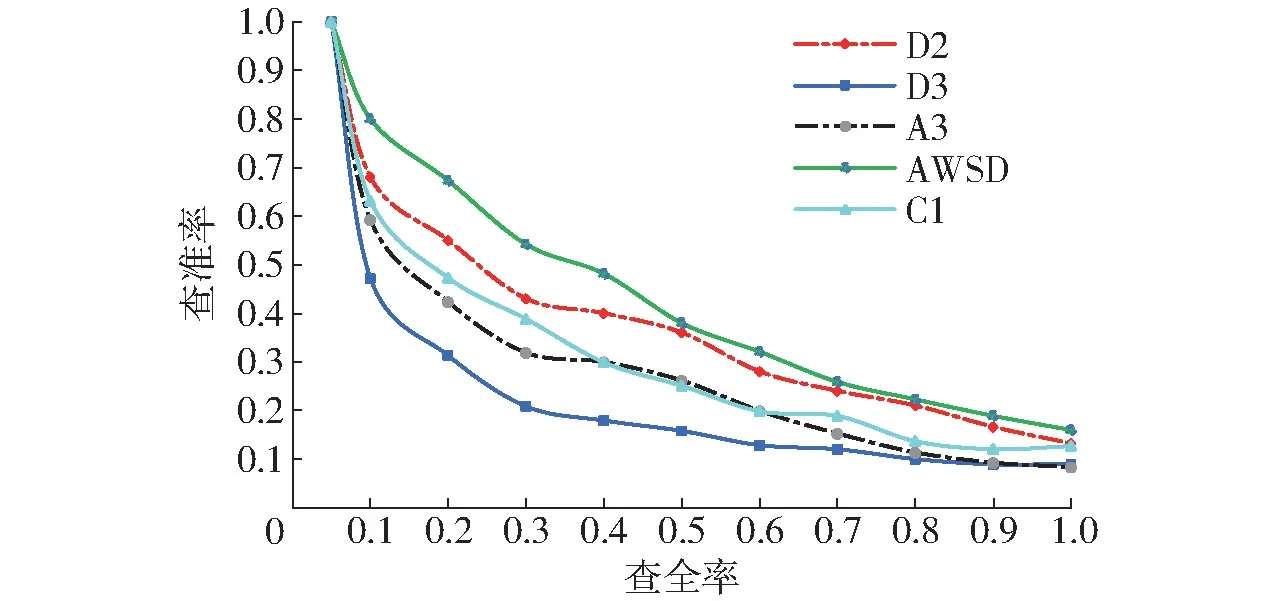
图6 查准率-查全率曲线Fig.6 Recall-precision curves
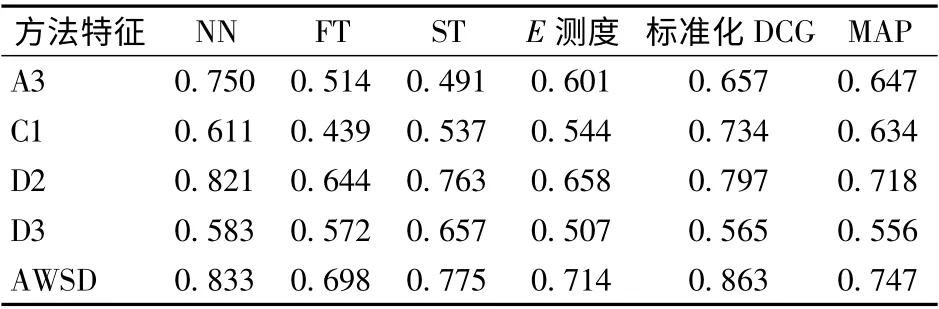
表3 农机模型检索效果Tab.3 Retrieval performance metrics
表4 给出了不同方法检索所需时间,由表4 可知,相对于单一特征提出方法,AWSD 特征融合方法特征提取时间、特征匹配时间不同程度增加,其平均检索时间为6.439 2 s,模型检索效率略有降低。综上可知,本文提出的AWSD 模型特征提取方法的检索精度与准确度均得到提高,检索效率符合要求。
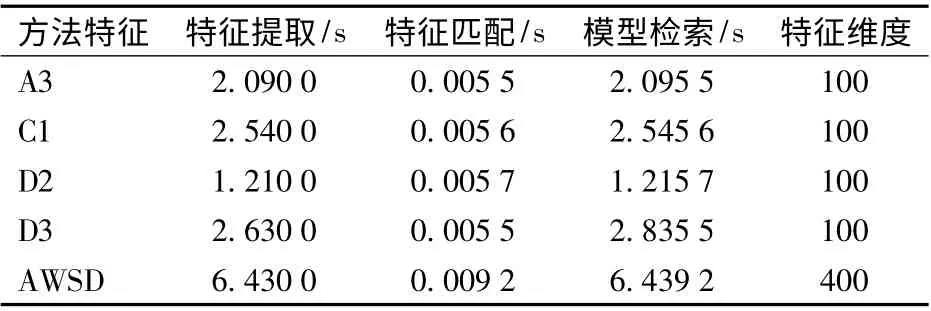
表4 模型检索所需时间Tab.4 Retrieval efficiency performance
3.4 应用实例
表5 为拖拉机轮毂CAD 模型检索结果,拖拉机轮毂的曲面特征最典型,因此选用曲率C1 形状分布算法与本文提出的AWSD 算法比较,距离D2 分布算法作为对照。由表5 可知,3 种算法均能够检索出同一类的6 个轮毂模型,视觉主观上可以观察出曲率C1 算法与AWSD 算法检索效果优于距离D2 算法,由此表明本文提出的AWSD 算法适用性较高,在检索主观满意度方面与专一特征检索算法近似。
摘穗板是玉米收获机割台的重要零部件[22],不同于拖拉机轮毂大类零件,常用摘穗板结构约10 种,表6 为模型库中摘穗板CAD 模型检索结果,其中与输入模型同一类的模型标记为黄色,非同类模型标记为灰色。由表6 可知,C1、D2 算法检索出4 种同类模型,而AWSD 算法能够检索出6 种,数量上AWSD 算法性能优于C1、D2 算法;输入的摘穗板模型含2 个方形槽,与其最相似的模型同样应为方形槽,但D2 算法首先返回U 型槽摘穗板,这可能由采样点随机性导致,此外距离D2 特征分辨率过低也将导致该现象发生。对检索后的模型进行简单尺寸、颜色编辑后即可设计重用,图7、8 为使用检索出CAD 模型进行快速设计的割台装配体。
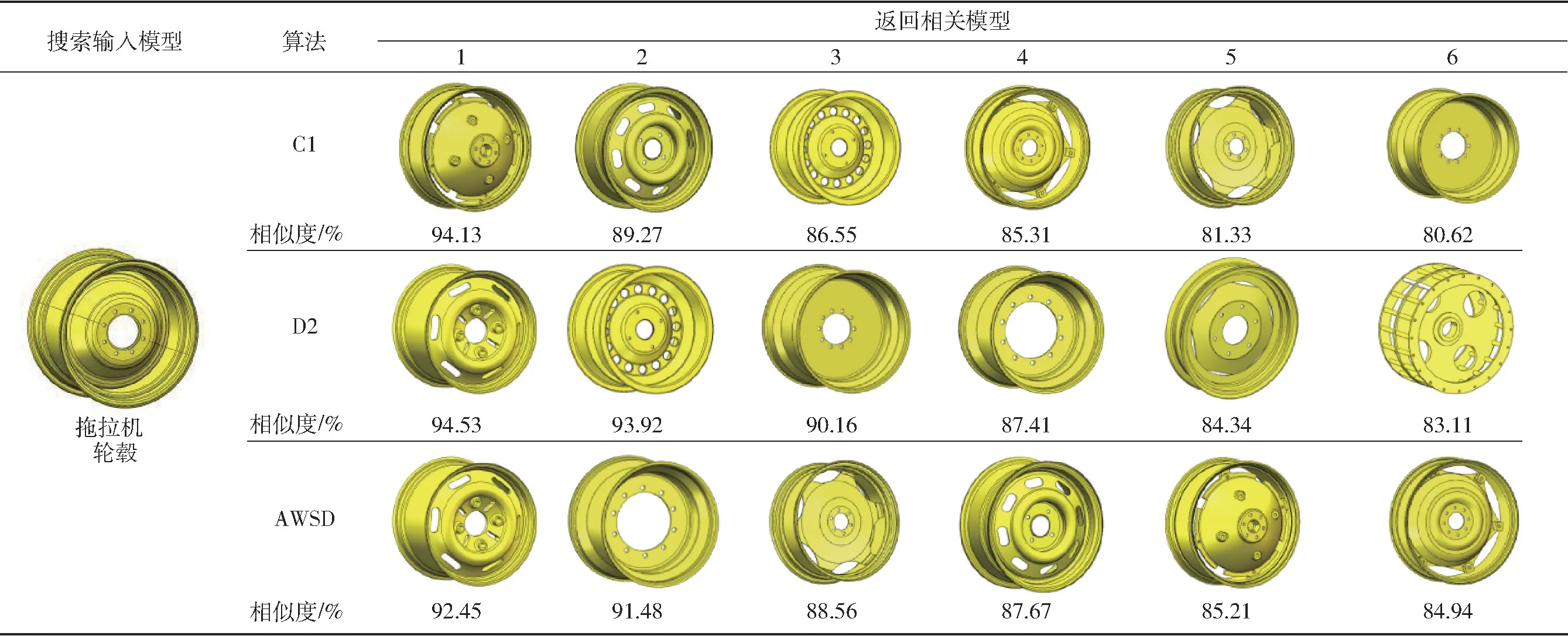
表5 拖拉机轮毂CAD 模型检索结果Tab.5 Retrieval results of tractor wheel hub model
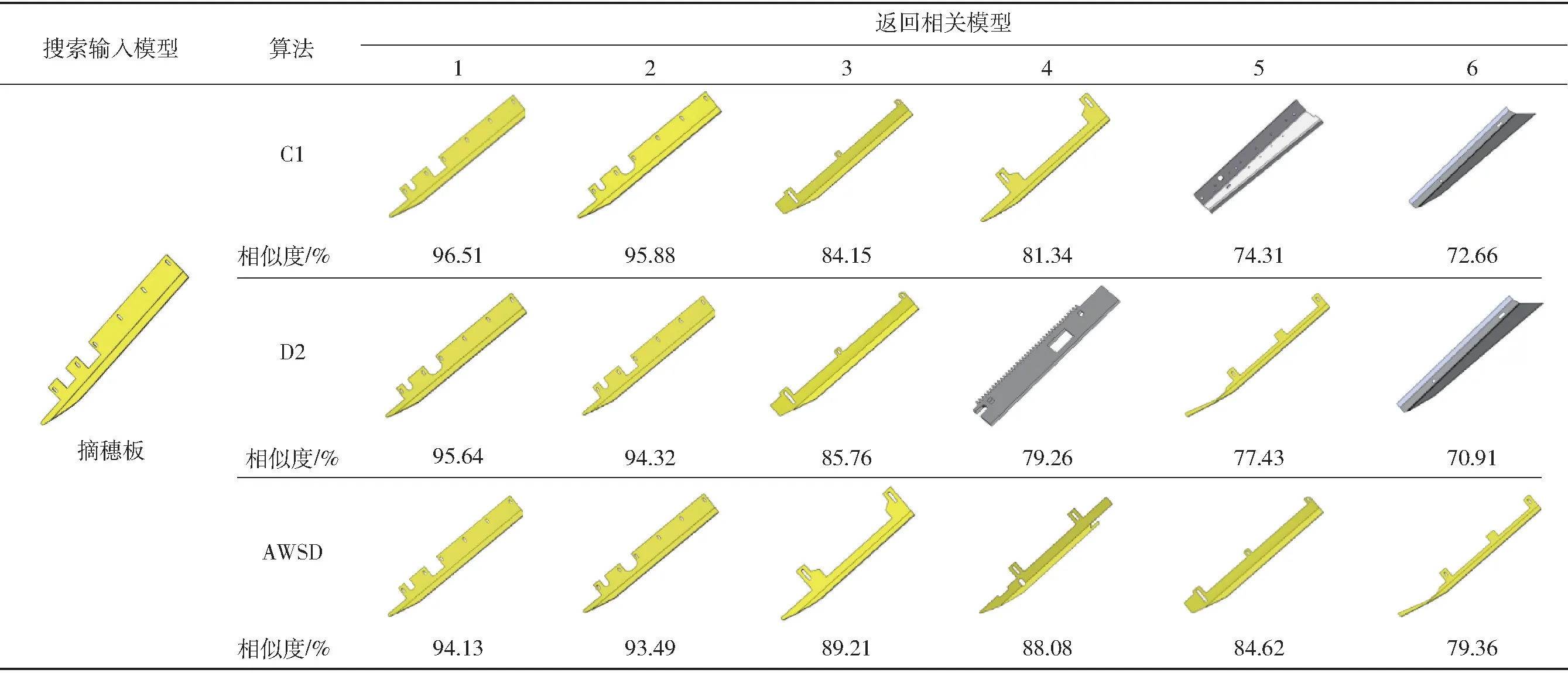
表6 收获机摘穗板CAD 模型检索结果Tab.6 Retrieval results of harvester picking board model
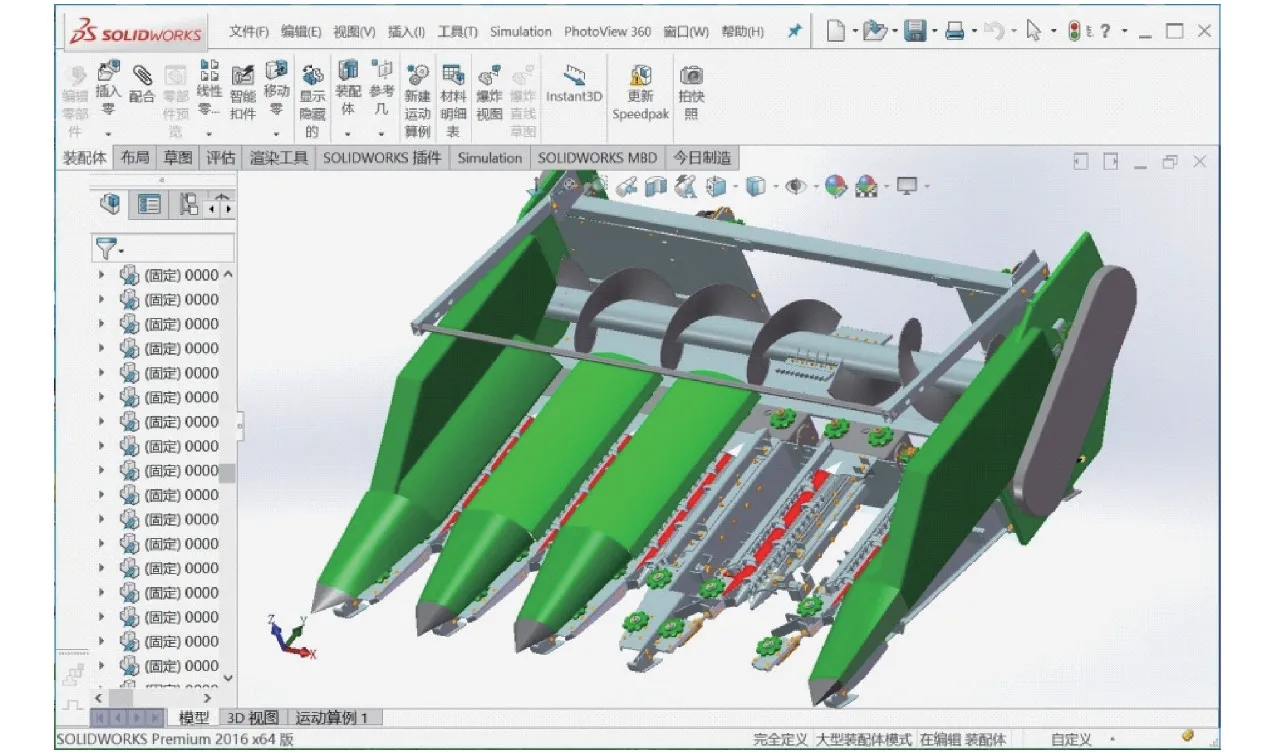
图7 玉米收获机割台Fig.7 Assemblies of corn harvester header
4 结论
(1)基于模型检索方式的设计重用方法将模型再设计问题转换为相关模型搜索,在模型数据库完备的情况下可有效降低设计成本、缩短设计周期。
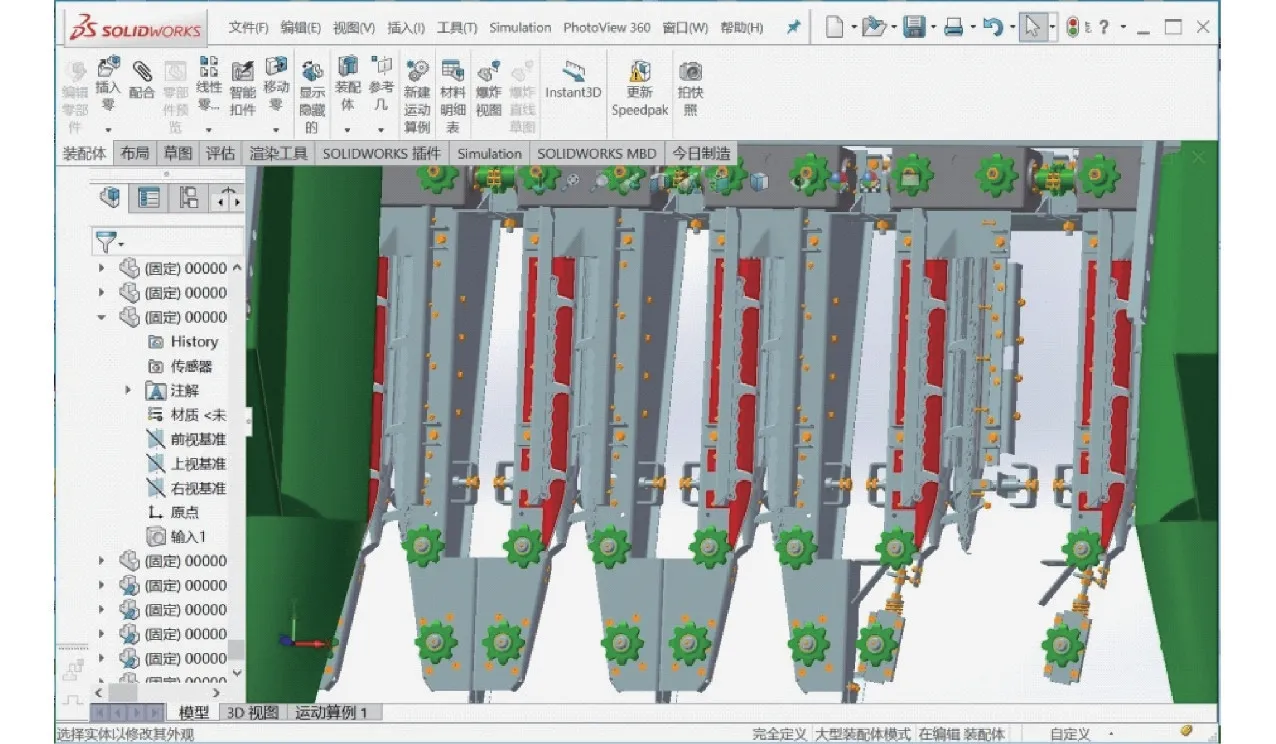
图8 玉米收获机割台局部Fig.8 Partial assemblies of corn harvester header
(2)单一形式的形状分布特征提取效果有限,通过计算特征值变异系数确定多特征动态权重,从而实现距离D2、面积D3、曲率C1、角度A3 多特征有机融合,融合后的特征不仅能够体现模型线与面、内部与表面、距离与曲率综合特征,而且能够有效弱化低区分度特征,突出模型特征的差异性,提高模型特征分辨率。
(3)提出的基于形状分布的AWSD 模型检索方法能够保持形状分布算法原有高稳定性的优点,对农机装备关键零部件模型库具有较高适用性,其综合检索精度较D2 形状分布算法提高了8.5%。

