基于平衡孔偏移的离心泵空化性能改善研究

王东伟 刘在伦 赵伟国

(1.兰州理工大学能源与动力工程学院，兰州730050;2.甘肃省流体机械及系统重点实验室，兰州730050)

0 引言

空化是离心泵内部流动的一种物理现象，是不可避免的一种流态。在离心泵运转过程中，空化将直接导致水力性能恶化，同时在空泡破灭位置会产生瞬间高压，造成材料表面破坏，并伴随强烈的振动与噪声，严重影响泵系统运行的安全性与稳定性［1-3］。

国内外学者针对离心泵空化流场做了大量研究。文献［4］利用PIV 技术与CCD 相机捕捉了叶轮内空化的发展过程。文献［5］采用SST k-ω 湍流模型分析了空化条件下离心泵泵腔内的不稳定流动。文献［6 -7］采用在离心泵叶片吸力面、流道中间以及叶片压力面布置监测点的方法，分析了叶片上与流道内压力脉动的变化特性。文献［8］通过数值模拟，分析了离心泵内空化瞬态特性，发现空化过渡过程中叶片上载荷随着空化的发展而变化，空化引起的漩涡导致叶片工作面产生较大载荷。

但针对离心泵空化性能改善方面的研究相对较少。文献［9 -10］通过在离心泵叶片表面布置障碍物及开槽的方法改善了离心泵的空化性能，发现布置障碍物可以有效增大叶片近壁面湍动能，叶片开槽可以有效阻止低压区域向外扩张，两种方法对空化各个阶段的发展均有抑制作用。文献［11］发现，在叶片表面开孔对离心泵空化性能的影响主要取决于流体在吸力面与压力面之间的能量差值与开孔后造成的能量损失之间的差，两者差值为正，则抑制空化，差值为负，则加剧空化。文献［12 -13］对穿孔翼型流场特性进行了研究，发现穿孔翼型改变了流场绕流条件，提高了低压区压力，而且单孔比多孔更有利于改善空化性能。文献［14］通过在翼型表面施加粗糙带，使得近壁面流场湍动能增加，提高了近壁面流场压力，进而抑制了空化初生的发生。文献［15］采用复合叶轮改善了离心泵内空化性能，指出长短叶片是提高空化性能的有效途径。文献［16-17］发现，在水翼表面布置射流水孔和在水翼吸力面布置凹槽的方法，在一定程度上可以抑制空化。

本文在前人研究工作的基础上，对平衡孔位置进行偏移，采用定常与瞬态模拟方法，对偏移前后离心泵内空化流场及轴向力变化进行分析，以期为改善离心泵空化性能和离心泵的优化设计提供参考。

1 计算模型

计算模型为单级单吸悬臂式离心泵，型号为IS150-125-250。基本参数:流量Qe=200 m3/h，扬程He=20 m，转速n = 1 450 r/min，比转数130，效率ηe=80%，表1 为模型泵过流部件基本设计参数。

表1 过流部件基本参数Tab.1 Specification parameters of flow passage component

本文采用Pro/E 软件生成三维计算区域模型，如图1 所示。为了保证计算的准确性建立了全流域模型。整个模型由叶轮水体、蜗壳水体、前后泵腔及进出口延伸段水体组成。

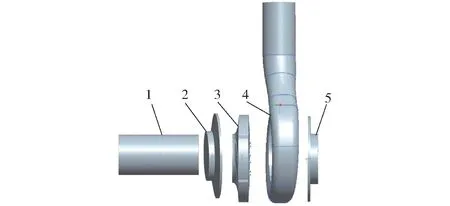
图1 模型泵三维模型Fig.1 3D structure of model pump

图2 为平衡孔偏移前后叶轮水体图，其中平衡孔直径为6 mm。参考原模型空化数为0.69 时叶轮中截面上空泡体积分数分布的计算结果，并根据各流道内空泡体积分数沿叶片背面分布长度的平均值选取偏移位置，偏移位置为叶片背面靠近进口边处，偏移后平衡孔中心距叶轮轴线半径为66 mm，同时为避免平衡孔出流对叶片背面造成冲击，偏移位置距离叶片背面取5 mm。

图2 平衡孔偏移前后水体模型Fig.2 Water model before and after balance hole offset

网格划分采用ICEM 软件，考虑到叶片曲面的复杂结构，对叶轮水体采用适应性较强的四面体网格，以便准确捕捉平衡孔附近流场的特征，蜗壳及其它过水段采用六面体结构化网格;针对网格数量对数值计算的影响，在额定工况下进行网格无关性检查，如表2 所示，当网格数大于280 万时扬程趋于稳定，考虑到计算资源最终网格总数取280 万作为网格的选取标准。

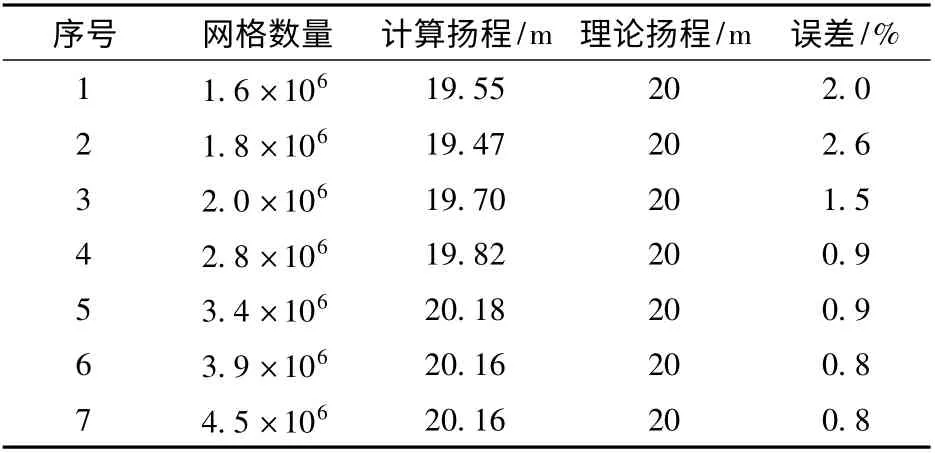
表2 网格无关性验证Tab.2 Grid independence test and verification

为保证数值计算精度，通常采用Y+来衡量近壁面区域是否有足够的节点数来捕捉边界层内的流动，其中Y+表示离壁面最近的网格节点到壁面的距离，为无量纲变量。本文采用Fluent 软件中RNG k-ε 湍流模型，Y+在300 以内则满足RNG k-ε 湍流模型对近壁网格质量的要求［18］。本次模拟近壁网格Y+最大值为120，能够保证在数值计算中具有较好的适用性。

2 数值计算方法

2.1 流动控制方程

流体运动基本控制方程为基于Reynold 平均的Navier-Stokes 方程［19］

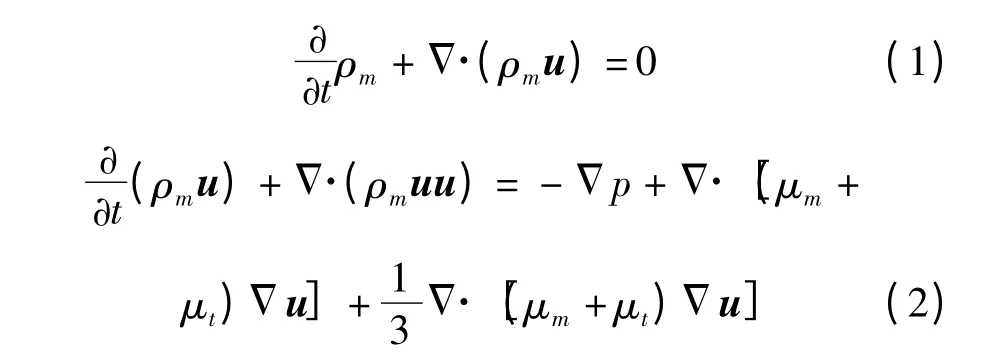
式中 t——时间

ρm——混合项的密度

μt——湍流粘性系数

μm——动力粘性系数，按气、液两相体积分数加权平均后获得

p——压力 u——速度矢量

2.2 空化模型

数值计算中采用基于Rayleigh-Plessset 方程的Zwart-Gerber-Belamri 空化模型，考虑气泡气化及凝结过程，得到质量运输方程为［20-21］

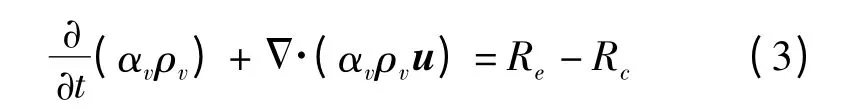
其中

式中 Re——单位体积质量蒸发速率

Rc——单位体积质量凝结率

Cvap——蒸发项经验系数，取50

Ccond——凝结项经验系数，取0.01

αv——气相体积分数

Rb——气泡半径，取10-6m

pv——水饱和压力，取3 540 Pa

ρv——气体密度，取0.554 kg/m3

αruc——成核位置气核体积分数，取5 ×10-4

ρl——液体密度，取997 kg/m3

2.3 边界条件

基于RNG k-ε 湍 流 模 型［22］和Zwart-Gerber-Belamri 空化模型;固壁表面为无滑移边界条件，进口条件设置为总压进口，出口设置为速度出口，系统参考压力设置为0;进口段与叶轮、叶轮与蜗壳以及平衡孔与后泵腔采用动静交界面耦合;前泵腔与蜗壳、前泵腔与进口段以及后泵腔与蜗壳采用静态交界面耦合;模型中未考虑容积损失及叶轮前后盖板与流体的摩擦损失。在额定工况下，首先对非空化流场进行定常数值计算，然后以此为初场并通过逐步降低进口总压的方法实现定常空化的数值模拟，并在定常空化计算的基础上进行瞬态数值计算，瞬态计算以叶轮旋转3°为一个时间步长，旋转一周总共120 个时间步长，每一步长的时间为Δt =0.344 8×10-3s，每个步长迭代30 次，计算时间为8 个叶轮旋转周期，并对第8 个旋转周期进行分析。

3 计算结果与分析

3.1 试验装置及外特性试验对比

为了验证计算方法的可靠性，针对模型泵进行了能量试验。试验在兰州理工大学能源与动力工程学院水泵实验室闭式试验台上进行。主要仪表有:泵进口压力传感器，量程为±0.1 MPa，精度为0.2级;泵出口压力传感器，量程为0 ～1 MPa，精度为0.2 级;LW-DN250 型智能涡轮流量计，量程为0 ～300 m3/h，精度等级为0.2;NJ1 型转速转矩仪，精度等级0.2，量程0 ～200 N·m。试验泵装置及示意图如图3、4 所示。

在试验过程中，即使所使用的测量仪器及测量方法完全符合国家规定，测量结果仍存在一定不确定性。因此本文通过多次试验对相关参数分别进行了不确定度分析［23-24］，结果如表3 所示。可以看到，各参数测量的不确定度均满足GB/T 3216—2016 中1 级验收等级的要求。

图3 试验泵装置Fig.3 Experimental setup

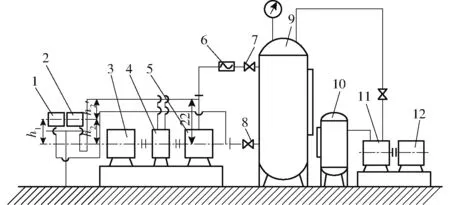
图4 离心泵闭式试验台示意图Fig.4 Sketch of test bed of centrifugal pump

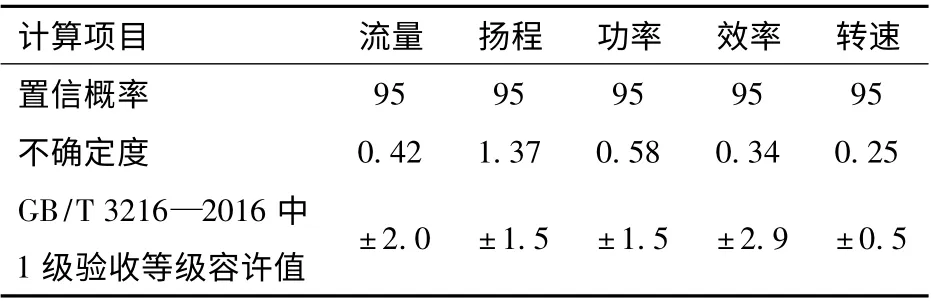
表3 不确定度计算结果Tab.3 Results of uncertainty calculation %

图5 为不同工况下平衡孔偏移前后，离心泵能量特性数值计算值与原模型泵试验值对比曲线。结果表明原模型模拟值与试验值吻合较好，扬程变化幅度在2%之内，效率变化幅度在3%以内;平衡孔偏移后模拟值与原模型试验值相比扬程降低在4%以内，效率降低在5%以内。额定工况点两模型扬程及效率与试验值误差均不到2%。

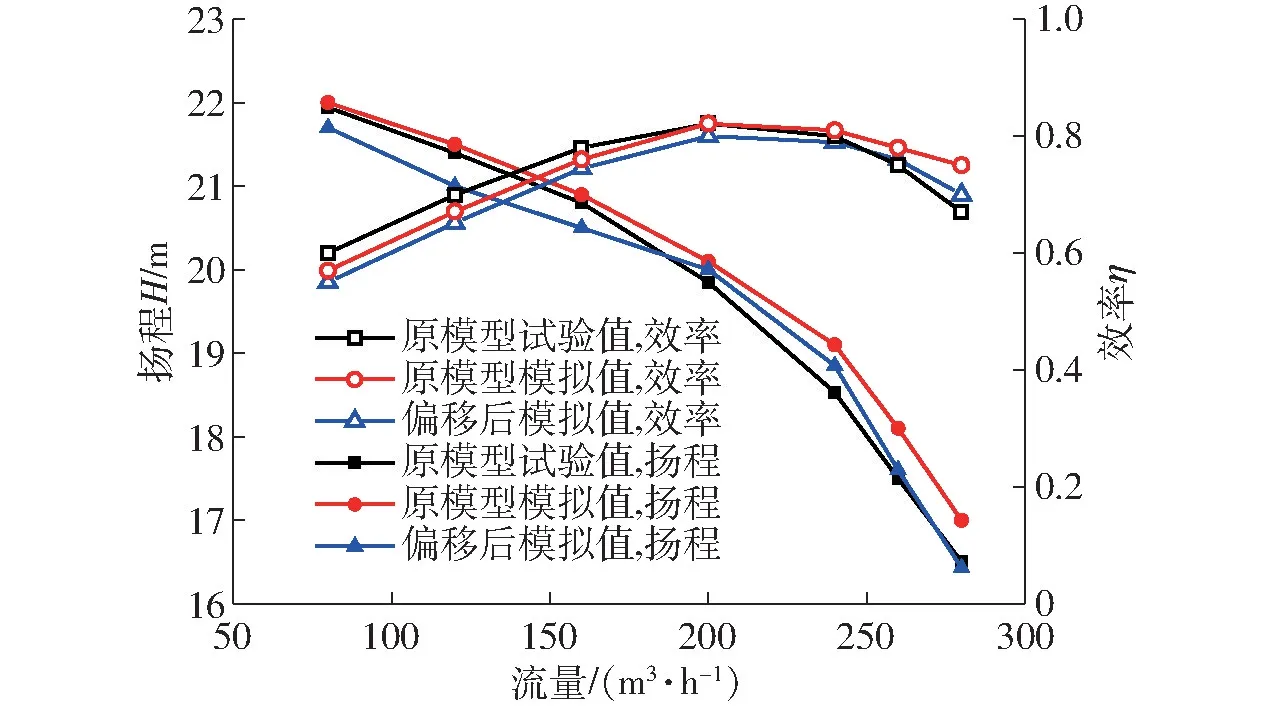
图5 外特性曲线Fig.5 Curves of external performance

3.2 空化特性验证

引入无量纲空化数σ，对数进行无量纲处理，其定义为

其中

式中 pin——基准静压力，采用泵进口压力，Pa

n——转速，r/min

ρ——流体密度，kg/m3

D1——叶轮叶片进口边与前盖板交点处直径，m

将1.2Qe、Qe及0.8Qe(Qe表示额定流量)流量下平衡孔偏移前后模型计算所得临界空化数与原模型泵试验结果进行对比，如图6 所示，可以看到平衡孔偏移后3 个流量下临界空化数均有所降低，可见平衡孔偏移后离心泵空化性能得到改善。本文以额定工况为例对空化流场进行了分析。

图6 临界空化数曲线Fig.6 Curves of critical cavitation number

图7 为原模型和平衡孔偏移后模型空化数与扬程计算结果及原模型泵试验结果的对比。可以看到，平衡孔偏移对空化性能曲线的影响，在空化初生及发展阶段影响不明显，当空化数为0.41 时，原模型扬程降低3%;而改型后模型在空化数为0.3 时，扬程降低3%，可见平衡孔偏移后临界空化数变小［25］，改善效果明显。

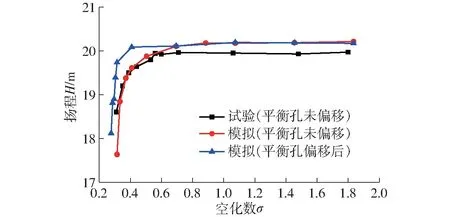
图7 空化性能曲线Fig.7 Curves of cavitation performance

3.3 平衡孔偏移对叶片背面压力的影响

通过对叶轮内部空化特征分析，发现额定工况下叶轮内空化主要发生在叶片背面，而低压区的演变是离心泵空化发展的主要原因，因此为分析平衡孔偏移前后叶片背面的能量特性，提取了不同空化数下叶片背面静压与动压分布图，同时为了使低压区压力梯度变化显示明显，限定压力上限值为20 kPa，如图8、9 所示。

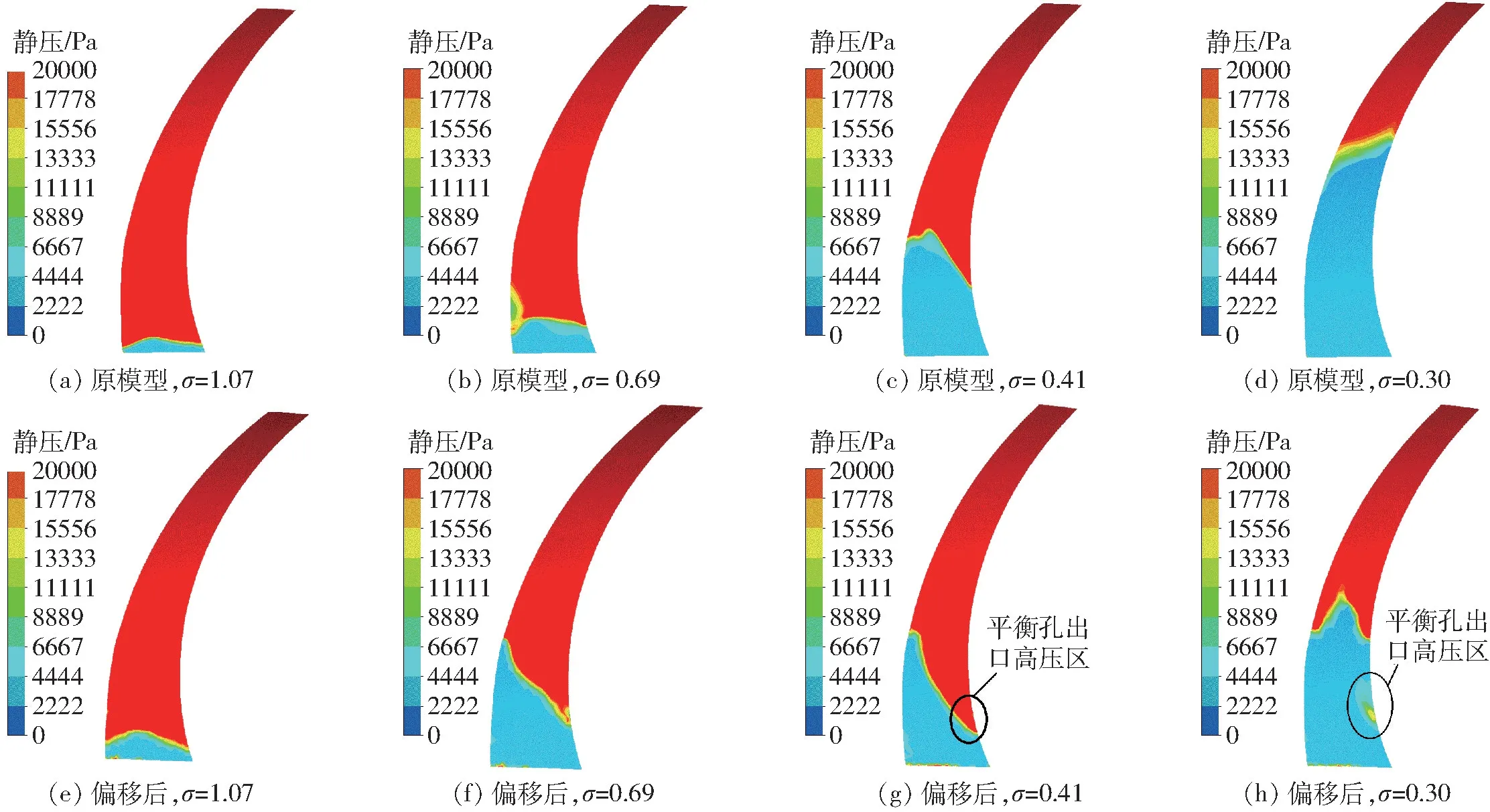
图8 静压分布Fig.8 Static pressure distributions

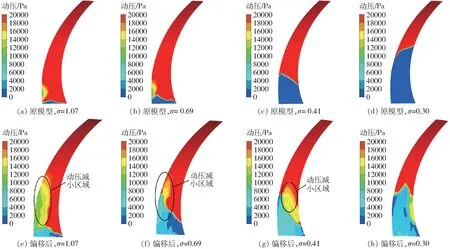
图9 动压分布Fig.9 Dynamic pressure distributions

图8 为不同空化数下叶片背面静压分布图。通过比较可以看出，随着空化数的减小，平衡孔偏移后叶片背面低压区表现出不同特征，在较大空化数时低压区面积有所扩大，但在空化数较小时低压区扩展却被延缓。当空化数σ 为0.41 即原模型对应临界空化数时，对比两模型发现由于平衡孔出流的原因在叶片背面形成了相对高压区，压力高于20 kPa，并产生了较大的逆压梯度，空化数σ 为0.30 时，此处静压最高值为14 kPa，如图8g、8h 所示。这说明平衡孔偏移后由其产生的出流能够提高出流口附近静压，改变此处压力梯度分布，进而影响空泡的生长。

图9 为不同空化数下，叶片背面动压分布图。通过对比发现，平衡孔偏移后叶片背面动压低压区面积扩大明显，说明此区域流体速度在一定程度上得到降低;结合图8 ～10 可见随着空化数的减小，虽然在平衡孔偏移后叶片背面静压低压区有所扩大，但空泡分布面积及体积分数却未增大，主要原因为此区域动压降低即流体速度减小，进而使得此处必需汽蚀余量减小，空化性能得到改善。综上所述，平衡孔偏移对叶片背面静压与动压均产生影响，在两者的共同作用下使得离心泵空化性能得到明显改善。

3.4 平衡孔偏移对气相体积分数的影响

移，相同位置上空泡的体积分数大幅降低，范围在0.4 ～0.9 之间，体积分数高值区域明显缩小，空化的发展得到了有效抑制;当空化数σ 为0.30 时即平衡孔偏移后对应临界空化数时，原模型泵中截面上空泡体积分数高值范围随着低压区的扩展不断向工作面延伸，流道有效过流断面面积大幅度减小，能量特性上表现为扬程大幅度降低;相比而言，平衡孔偏移后在相同位置虽然空泡区域面积也有所增大，但是体积分数高值区域相对较小，主要集中在空化区域沿叶片背面发展的前部，而在靠近叶片进口附近区域体积分数为0.6 ～0.8，而此处正是平衡孔偏移位置;同时个别流道体积分数高值区域出现了明显的断裂，可见平衡孔偏移后空泡的连续性被破坏，体积分数分布改变。综上所述，平衡孔偏移对空化的发生发展具有明显的影响，可以有效抑制空泡的发展。

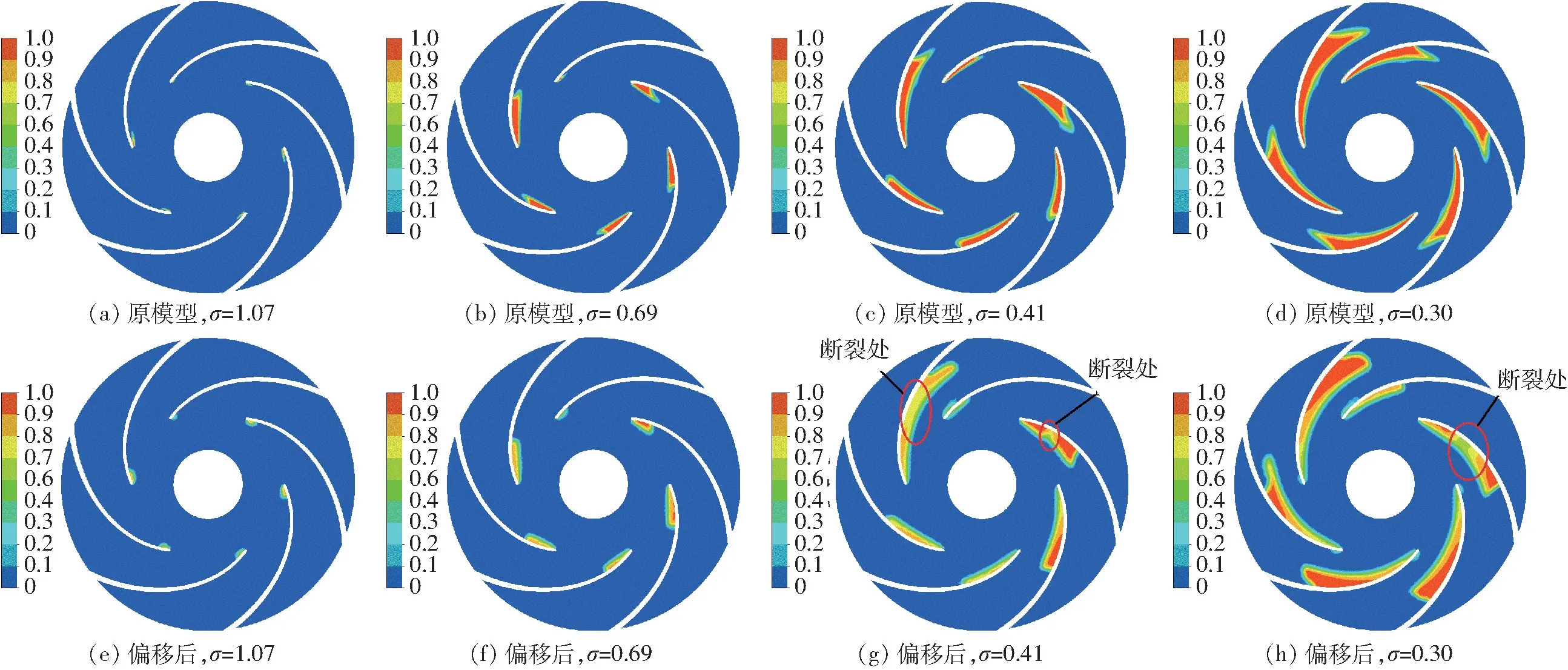
图10 气相体积分数分布Fig.10 Distributions of vapor phase volume fraction

3.5 平衡孔偏移对湍动能的影响

图11 为不同空化数下，叶轮中截面上湍动能分布图。湍动能可以反映流道内流体湍流所具有的能量，湍动能越大流场越不稳定。通过图11 发现，平衡孔移动前后在相同空化数下叶轮内湍动能变化明显。结合图10、11 可以看到，在原模型中湍动能较大区域主要集中在空泡区域后部，随着空化数的不断降低，空泡体积分数高值区域不断增大，湍动能高值区域也不断增大，致使流道内流动条件变差，水力损失增加。平衡孔移动后，由于平衡孔出流的作用使得在相同流道内空泡体积分数大幅度下降，如图10 所示，因而减弱了空泡区域对其后部流场的扰动，使得湍动能高值区域明显减小。可见，平衡孔偏移对空化流场改善明显。

3.6 平衡孔偏移对空泡体积的影响

为了分析平衡孔偏移前后叶轮内部空泡体积变化特征，引入空泡体积Vcav并对空化数分别为0.69、0.41 及0.30 工况下，平衡孔偏移前、后模型的空化流场进行非定常计算。

叶轮内部空泡体积Vcav定义为

式中 m——叶轮内总控制单元数

αv，i——控制单元内气相体积分数

Vi——每个控制单元体积，mm3

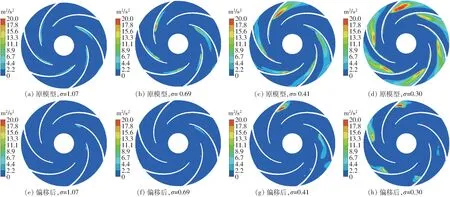
图11 湍动能分布Fig.11 Distributions of turbulent kinetic energy

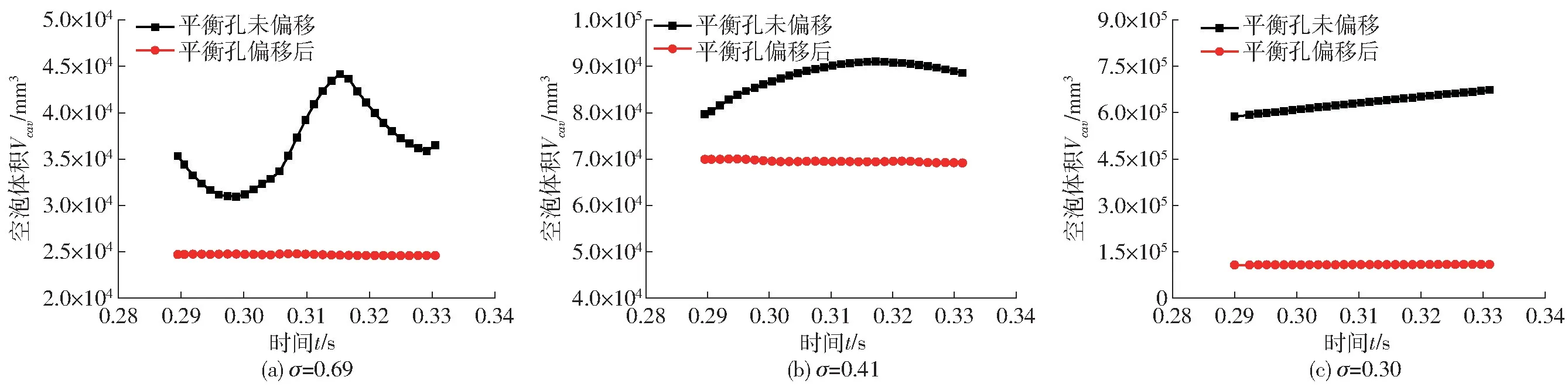
图12 空泡体积变化曲线Fig.12 Change curves of cavitation volume

图12 为叶轮流道内空泡体积在一个叶轮旋转周期内随时间的变化曲线，可以看到空化数σ 为0.69 时，平衡孔偏移前后叶轮内空泡体积波动较为稳定，平衡孔偏移后空泡体积明显小于偏移前;当σ为0.41 即原模型对应临界空化数时，原模型叶轮内空泡体积增大明显，其最大值接近1.0 ×105mm3;相比之下平衡孔偏移后叶轮内空泡体积增长较为缓慢，数值上基本维持在7.0 ×104mm3附近;当σ 为0.30 即平衡孔偏移后模型对应临界空化数时，此时原模型扬程已急剧下降，泵内空泡大量产生，空泡体积在整个周期内处于增长趋势，而平衡孔偏移后模型空泡体积较为稳定，基本处于1.3 ×105mm3附近，略高于σ 为0.41 时原模型叶轮内空泡体积。由此可以看出平衡孔偏移后改善了流动条件，抑制了空泡体积的增长。

3.7 平衡孔偏移对轴向力的影响

离心泵在运转过程中由于前后泵腔体压力不等、叶轮内部流动的不对称性及自身结构等原因，在转子上将产生轴向力，成为影响泵安全、稳定运行的重要因素。叶轮上开平衡孔就是平衡轴向力的主要方式之一，按照具体产生的原因，离心泵轴向力主要由以下各部分组成［25-26］:叶轮前、后盖板面积不对称产生的轴向力F1、F2;扭曲叶片上产生的轴向力F3;由叶轮流道内压力分布不均所产生的轴向力F4;流体流过叶轮产生的动反力F5;平衡孔平衡力F6。为了进一步分析平衡孔偏移后对轴向力的影响，通过数值模拟得到了0.8Qe、Qe及1.2Qe工况下平衡孔偏移前后轴向力，如表4 所示，其中负号表示力方向由叶轮后盖板指向泵进口。由表4 可知，平衡孔偏移前后总轴向力变化趋势相同，均随流量增大而减小，且方向相同未发生变化;但相比于原模型，平衡孔偏移后总轴向力在0.8Qe、Qe及1.2Qe工况下分别减小了18.9%、25.0%、5.9%，可见总轴向力在平衡孔偏移后均有所减小，额定流量下总轴向力减小最为显著;在各分力中前盖板处轴向力F1在0.8Qe及Qe工况下增大较为明显，其它分力变化较小，是轴向力减小的主要原因;1.2Qe工况下多数分力均有小幅度的减小;可见，平衡孔偏移后可以在一定程度上减小轴向力，改善了受力条件。

4 结论

(1)平衡孔偏移后，各工况下扬程、效率均有所下降，扬程降低幅度在4%之内，效率降低幅度在5%以内;临界空化数σ 由原模型0.41 减小到0.30。可见，此方法对空化抑制效果明显。

(2)平衡孔偏移由于平衡孔出流作用改变了叶片背面空化区域的静压分布，延缓了较小空化数时静压低压区的扩展;同时，平衡孔出流改善了叶片背面空化区域附近流场，降低了此处流动速度，从而减小了必需汽蚀余量，提高了离心泵空化性能。

表4 轴向力计算值Tab.4 Numerical value of axial thrust N

(3)平衡孔偏移对叶轮内空泡体积分数影响明显。在相同空化数下，平衡孔偏移后叶轮内空泡体积分数降低，部分流道内空泡体积分数高值区出现了断裂，空泡的连续性遭到破坏，抑制了空泡的发展。

(4)与原模型相比，平衡孔偏移后在0.8Qe、Qe及1.2Qe工况下总轴向力均减小，在一定程度上改善了离心泵的受力。其中，在0.8Qe及Qe工况下总轴向力减小幅度最大，分别减小了18.9% 与25.0%。可见，平衡孔偏移不仅可以改善离心泵空化性能，而且可以减小总轴向力。