正态分布产品的Bayes可靠性抽样检验方案
王燕飞
(吉林化工学院 理学院,吉林 吉林 132022)
可靠性抽样检验是通过检查产品的样本质量来评价整批产品质量.随着科技进步,产品的可靠性越来越高,应用经典统计方法制定的可靠性抽样检验方案的抽样量较大.因此,人们越来越重视应用Bayes统计方法制定可靠性抽样检验方案,以便充分利用产品的各类可靠性信息,从而有效地降低可靠性试验的抽样量.
在实际生产生活中,很多产品的性能指标都服从正态分布,非常普遍.但关于正态分布产品的可靠性抽样检验的研究成果却较少.冯文哲、刘琦基于0—1损失函数和两类风险约束条件,研究了正态型指标的复杂假设的Bayes可靠性验证试验设计[1].张硕云等对于正态型指标的简单假设,利用Bayes方法基于两类风险确定了样本量[2].很多产品的指标是要求在规格上限与规格下限范围之间鉴定为合格,否则认为不合格.关于正态型产品的双侧规格限情形的可靠性抽样检验问题,国家标准GB8053—87[3]没有明确方案.国际标准ISO3951:1989(E)和国家标准GB6378—86只有图方法,没有数值方法.美军标MIL-STD-414和美国标ANSI/ASqCZI 1.9也仅是得到近似的抽样方案设计.吕建华、吴启光利用经典统计方法,探讨了综合双侧规格限下方差未知的正态分布产品的可靠性抽样检验方案[3].
事实上,正态型产品的指标值多数都为正值.这一信息往往被忽视.针对正态分布指标的双侧规格限情形,研究了在总体方差已知,总体指标的均值为正的前提下,根据Bayes理论,确定最大熵先验分布,并求得后验分布.利用生产方和使用方的两类风险约束条件,确定最小抽检样本量,从而制定更加合理有效的抽样检验方案.最后通过实例说明其效果优于经典统计方法确定的抽样检验方案.
1 基于最大熵先验的正态指标的可靠性抽样检验设计模型(MENBR)
假设产品的某性能指标X服从正态分布N(μ,σ2).其中σ2已知,指标均值μ>0.为了检验该指标均值是否达标,抽取样本X1,X2,…,Xn,其观察值为x1,x2,…,xn.
产品的生产方和使用方根据产品性能的可靠性要求,共同协商建立如下统计假设:
H0:L≤μ≤U,H1:μ>U或0<μ 其中L为指标值的规格下限,U为指标值的规格上限.即产品指标均值满足L≤μ≤U时认为合格,否则认为不合格. 根据Bayes理论,为了对产品指标进行检验,需要利用指标值的后验分布[4].首先依据一些先验信息确定μ的先验分布.根据以往历史数据资料,容易得到μ的样本均值,近似估计总体均值.若E(μ)=θ(μ>0),则除此之外没有其他信息可用.那么在这样的前提条件下,确定最“无信息”的先验分布是非常合理的,即最大熵先验[5]. 证明:根据文献[4],可知,若满足条件 Eπ[gk(μ)]=θk(k=1,2,…,m), 其中gk(·),μk(k=1,2,…,m)分别表示已知的函数和已知的常数.则此时μ的最大熵先验分布为 其中π0(μ)为μ的无信息先验. 当λ1≥0时,π(θ)=0.无意义;当λ1<0时,π(θ)=-λ1eλ1θ. 下面利用μ的先验分布及总体分布确定μ的后验分布,得到如下定理2. (1) 故T的边缘分布为 则μ的后验分布为 对产品指标进行可靠性抽样检验,对于生产方最关心的是:由抽样得到批产品没有通过检验,而产品的性能指标值却是合格时的风险.换言之,在抽样检验统计量T∈W(W为检验的拒绝域)时μ∈[L,U]的概率.则生产方所承担的最大风险即为后验概率 对于使用方而言,最关心的是通过抽样批产品通过检验,但产品指标却是不合格时的风险.或者说,在抽样检验统计量T∉W(W为检验的拒绝域)时μ∈(-∞,L)∪(U,+∞)的概率.则使用方所承担的最大风险即为后验概率 通常,生产方和使用方的最大风险分别限定在给定数值α和β值以内.由此可知,可靠性抽样检验方案的制定,就是求解方程组 (2) 从而确定最小抽检样本量.将方程组(2)称为基于最大熵先验的正态指标的可靠性抽样检验设计模型(MENBR). 对于模型MENBR,拒绝域W的确定尤为关键.根据Bayes假设检验理论,当后验概率 P(μ∈Θ1|T=t)≥P(μ∈Θ0|T=t) (3) 时拒绝原假设H0. 将后验分布(1)代入(3)中,化简得: (4) 即当T满足(4)式时,拒绝原假设H0,则此时的T的范围即为拒绝域W. 为了求解拒绝域W,可以利用Matlab编程.具体编程步骤如下: 建立函数 2.编制两个子程序: 子程序1: 子程序2: 3.运行子程序1和子程序2,可以分别得到临界点C1和C2. 通过Matlab程序搜寻结果可得到,T的拒绝域W=(0,C1)∪(C2,+∞). 下面将拒绝域W=(0,C1)∪(C2,+∞)代入方程组(2),即可得到最小检验样本量n, 从而确定模型的Bayes抽样检验方案(n,C1,C2). 假设某种产品的指标值为X,且X~N(μ,σ2).根据历史数据得到,该产品指标的总体方差为σ2=16,利用平均指标的数据求得的期望为E(μ)=350=θ.若生产方和使用方协商确定产品的规格下限和规格上限分别为L=346,U=355.通常,生产方承受最大风险限定值为α=0.05,使用方承受最大风险限定值为β=0.10.则利用Matlab搜寻得到拒绝域W的临界值为346.7和354.8.故T的拒绝域为W=(0,346.7)∪(354.8,+∞),将其代入方程组(2),得: 从而确定最小检验样本量为44. 即得到模型的Bayes抽样检验方案(44,346.7,354.8).这比经典统计方法确定的最小抽检验本量68要小得多.并且较之经典统计方法,该方法更加简便易行. 本文针对正态分布型产品的指标值为正,且总体方差已知,平均指标值为已知常数的情况,利用最大熵原理确定指标值的先验分布,根据Bayes理论确定可靠性抽样检验方案.在求解过程中,运用Matlab软件编程搜索拒绝域的临界值,并由生产方和使用方的最大承担风险确定最小抽样样本量.这种确定可靠性鉴定试验方案的方法,对于正态型分布产品的双侧规格限情况,有较大突破,避免了传统的经典统计方法的繁琐计算.最终得到的最小抽样检验量也更加节约经济,效果很好.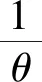

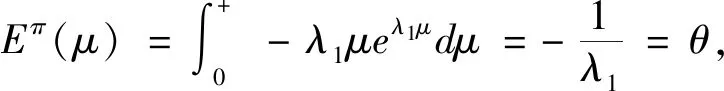
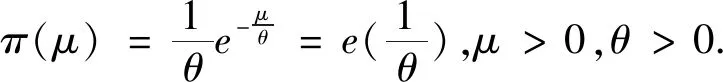

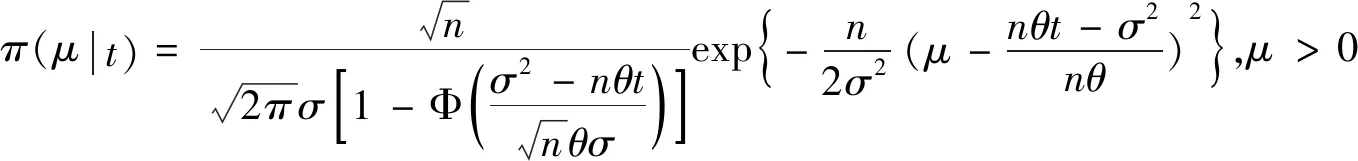
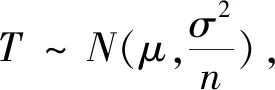


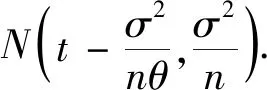



2 模型的求解

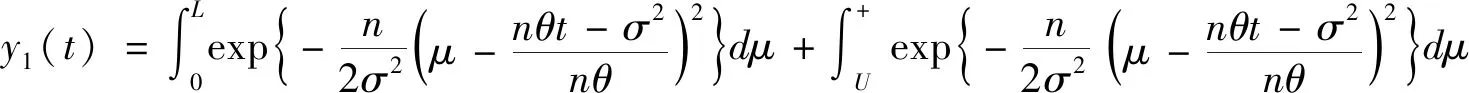
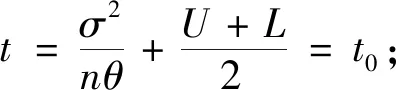
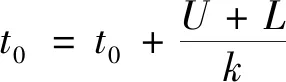
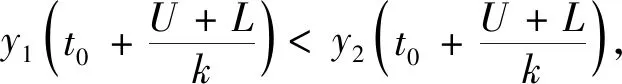

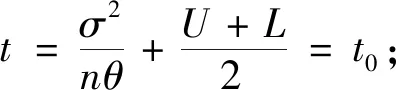
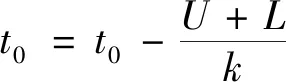

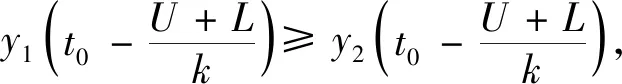
3 算 例
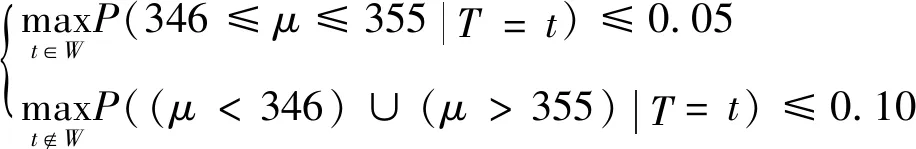
4 结 论

