基于室外温度的供热负荷预测研究

孟亚男,姚 洁

(吉林化工学院 信息与控制工程学院,吉林 吉林 132022)

我国是一个建筑大国.根据能源行业过去30年的研究结果和做法，建筑业的能源效率是最有潜力和最直接的节能形式，而在建筑业能源效率中供热节能占比又很大[1].为了节能降耗，我国热力行业已经开始将集中供热逐渐取代分散式供热[2].集中供热虽然有效地提高了冬季人们生活环境温度的舒适度，但由于在调控和技术管理方面大都采用粗犷的方式，导致目前集中供热存在着较为严重的能耗问题，使得供热成本出现了不降反增的现象[3].为此，为了减少供热成本提出了供热负荷预测来降低能耗.

研究了室外温度与热负荷在气象因素中的关系，以期提供一个较为准确的热负荷预测模型.研究采用数据回归分析进行供热负荷预测，并运用最小二乘法消除预测值和样本之差的平方和，得到精准的回归系数.热负荷预测是根据室外温度作为输入参数来进行预测的.

1 供热负荷影响因素

热负荷预测的影响因素有时刻变化的室外气象因素以及供热设备结构的传热系数.较大规模的集中供热系统中，传热系数通常被视为常量，而室外温度、风速、光照等气象因素具有时变性的特点.但风速、光照对于热负荷影响很小.又因在建立回归方程的过程中若把所有可能产生影响的因素全部考虑进去，得到的不一定是最好的模型.因此只选用对供热负荷有显著的影响的室外温度作为主要因素.

2 供热负荷预测模型建立

2.1 热负荷计算公式

一般情况下换热站供热负荷与室外温度的计算公式[4]，如下所示：

(1)

Qi:供热负荷,MW；Cq:水的比热容常数值；Fg:供水流量,t/h；Tg:供水温度,℃；Th:回水温度，℃.

2.2 一元线性回归模型建立

线性回归模型建立，选供热负荷、室外温度分别为因变量、自变量，回归模型如下：

y=d0+d1x1，

(2)

d0：需要确定的系数；x1：室外温度.

(3)

(4)

3 数据来源和数据预处理

3.1 数据来源

以某换热站2018年～2019年中1月～3月的室外温度、供水流量、供水温度、回水温度83组历史数据并根据历史数据算出热负荷值.

3.2 数据拟合结果

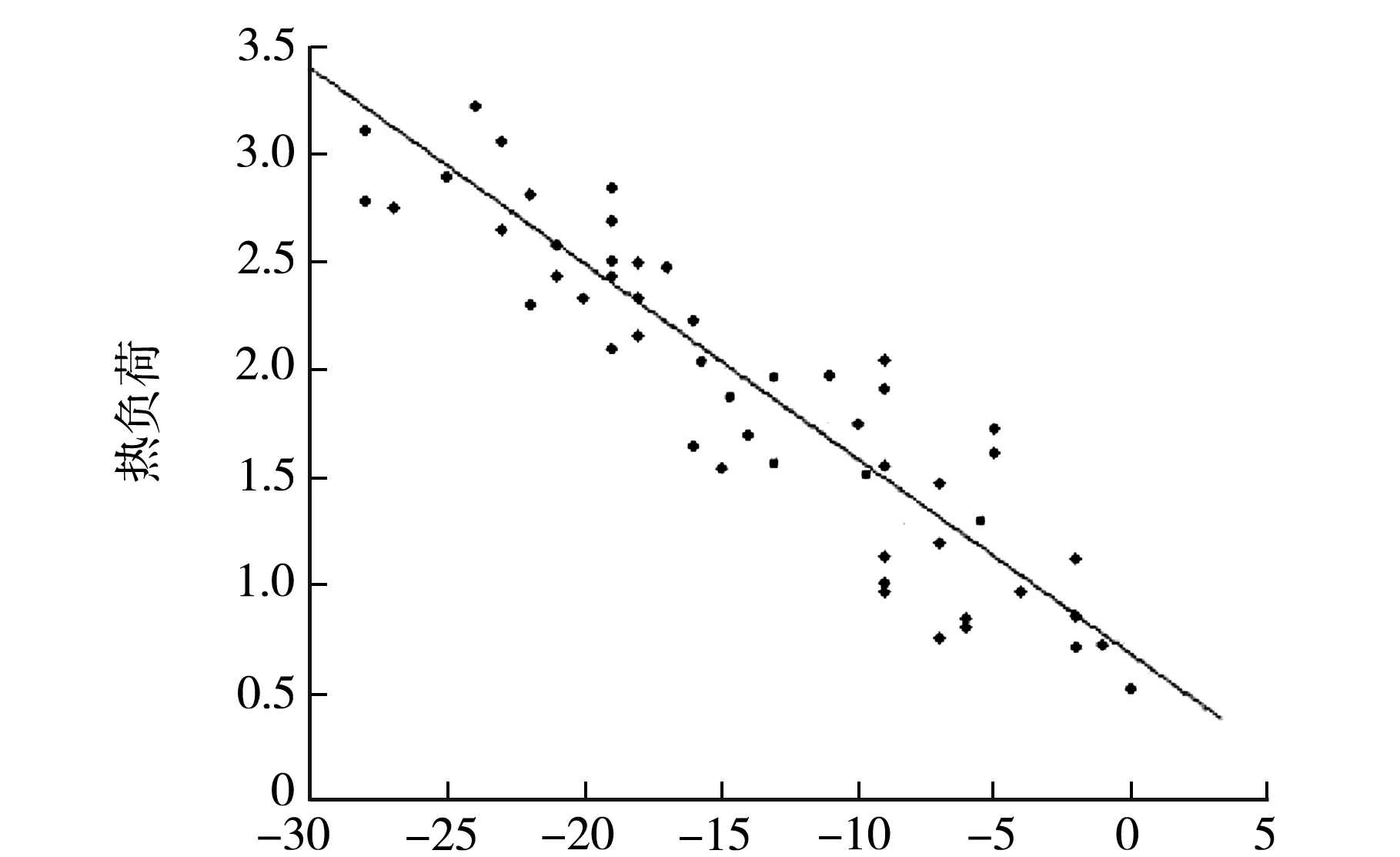
确立模型并利用最小二乘法，根据历史数据计算回归系数d0,d1，流程图如1所示.数据拟合直线图如图2，表1为建模数据.

图1 最小二乘法实现流程

室外温度/℃图2 初始数据室外温度与热负荷拟合直线

得到一元回归拟合方程式为：

y=-0.108x+0.665，

(5)

由图2可知，数据存在异常点，而直接影响分析结果的因素就是这些奇异点的存在，为此降低异常点应要在数据分析之前进行数据预处理.

3.3 数据预处理

历史热负荷数据中不可避免的包含一些不良数据或伪数据，这是因为记录历史采暖热负荷时，可能存在人为、数据传输、系统故障、测量设备误差等因素[5]，可用拉依达准则法将奇异点去除.为得到两个变量之间的线性关系，将通过最小二乘法拟合，得出样本距，拉依达法的输入样本为得出的样本矩，并运用贝塞尔计算标准差估值，根据拉依达准则进行判断，样本残差大于3δ标准差估计值，就被视为异常值，并将该数据剔除.

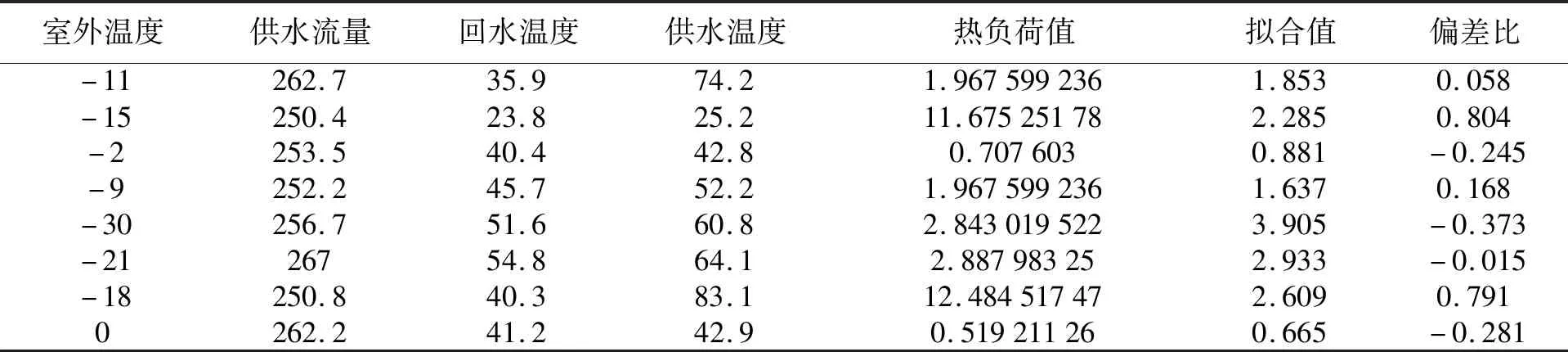
表1 热负荷建模数据

用拉依达准则对数据进行多次处理直到得出满足条件的数据为止，并将它们进行拟合，最后预处理数据拟合效果如图3，数据处理后的热负荷数据如表2所示.

表2 部分数据预处理建模数据

部分数据预处理编程如下：

Delflag=0；

for i=1:1:length(data2.MaxTemp)-1

if d(i) > 3*sigma

DelData(Delcount,:)=data2(i,:)；

Delcount=Delcount+1；

data2(i,:)=[]；

Delflag=1；

end

end

if(Delflag==0 )

break；

end

室外温度图3 处理后的热负荷与室外温度的拟合直线

数据处理后得到的热负荷预测模型的表达式：

y=-0.09x+0.682，

(6)

由图3可知，对历史数据处理后更具有线性回归性，比没剔除粗大误差时拟合的效果要理想,并且有着比较小的误差.同时本文方法的检验统计量F大于临界值[6]，也说明了线性回归效果显著.

4 结 论

首先分析并确定了供热负荷回归模型所需的自变量，并通过分析与检验证明了所选自变量与因变量的相关性，利用标准差估值并通过拉依达准则剔除历史数据中异常点，后重新建立的数学模型是可行的.根据拟合结果可知，室外温度可以对供热负荷量的计算起到一定的预测效果.同时也为热负荷预测的供热量提供了参考价值.