模糊故障树和FMECA的数控机床综合评价方法
冯昊天,王红军,2,3,曹 翔,王鹏家
(1.北京信息科技大学机电工程学院,北京100192;2.高端装备智能感知与控制北京市国际科技合作基地,北京100192;3.北京信息科技大学现代测控技术教育部重点实验室,北京100192;4.成都飞机工业(集团)有限责任公司,成都610092)
0 引 言
可靠性是产品的重要质量指标,它标志着产品能够进行正常生产工作的可能程度。从经济学角度看,为了提高产品的利用率,降低故障发生频次,高可靠性是非常必要的[1]。
研究人员通常利用概率统计方法将产品发生故障的规律作为随机现象来研究。张根保等[2]对传统的机床可靠性分析方法进行了总结:一般通过计算平均无故障间隔时间(MTBF)、失效前工作时间(MTTF)等统计指标分析各机床可靠性信息;通过故障模式、影响和危害性分析(FMECA)、故障树等分析方法对机床各主要故障部位进行分析,得到危害度、重要度等指标,从而提出改进措施[3]。
由于在实际应用中故障的发生具有随机性,而传统的分析方法需要精确的故障数据信息进行分析[4-6]。陈友玲等[7]在故障树分析方法的基础上,引入模糊集合论的概念,使用三角模糊数表示故障概率,求得各故障模糊重要度,从而解决实际工作中数据必须准确的问题。鞠萍华等[8]提出一种装配序列多目标模糊综合评价方法,运用模糊层次分析法实现对改进方案的优化。以上方法在传统分析方法的基础上结合模糊集合论思想,求得更为准确的模糊重要度,一定程度上解决了故障随机性问题。
目前,一些学者对传统分析方法的综合运用进行了研究。王桂萍等[9]运用故障比重比对某加工中心进行综合分析;王汉伟等[10]运用模糊综合评价求得各评价指标权重。以上方法将传统分析方法进行整体分析,考虑更为全面。本文运用模糊集合论及综合指数评价分析,通过模糊故障树分析及FMECA求得故障模糊重要度及危害度,并对其进行综合指数评价分析,得到各故障综合指数。
1 综合指数评价分析
利用模糊故障树得到模糊重要度后,通过FMECA方法求得各故障危害度。然后使用综合指数评价分析方法对故障危害度及模糊重要度进行综合分析,并对各故障部位按综合指数降序排列,该过程如图1所示。机床用户可根据排列顺序了解该类机床可靠性情况,并做出针对性维护,从而提高生产效率,降低维修时间。
1.1 模糊故障树分析
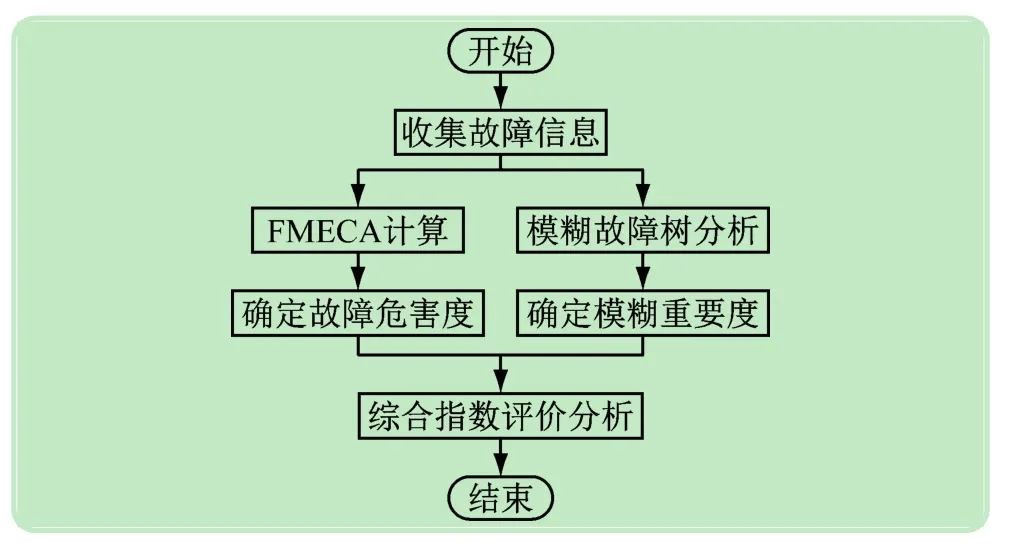
图1 综合指数评价分析过程图
(1)故障树分析方法。传统故障树分析中,顶事件的失效概率是利用逻辑门算子对基本事件发生概率进行运算获得的,因此知道基本事件的发生概率和结构函数就可以唯一确定系统顶事件的发生概率P。
设F1为故障树所有最小割集出现的概率之和;F2为所有最小割集两两同时出现(即交集)的概率和;F3为所有最小割集三三交集出现的概率和[12]……,则按概率法则,顶事件出现的概率为:
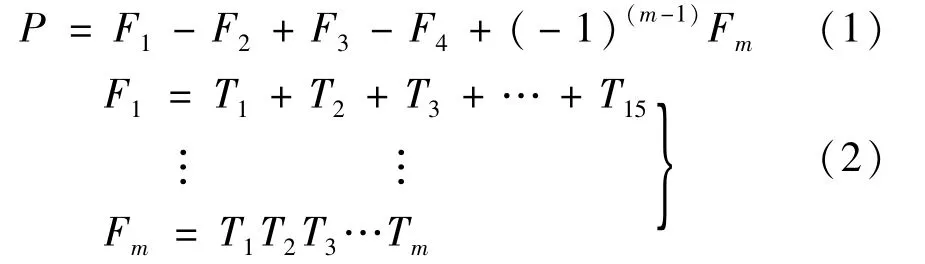
(2)模糊集合论。模糊集合论中,利用三角模糊数来描述基本事件发生的概率,用模糊逻辑门算子代替传统的逻辑门算子,从而得到顶事件的模糊失效概率(见图2)[13]。
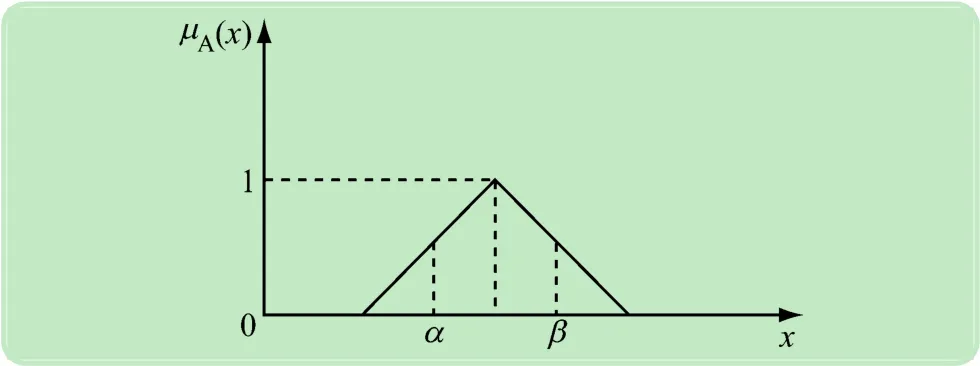
图2 三角模糊数函数
三角模糊数隶属函数为:
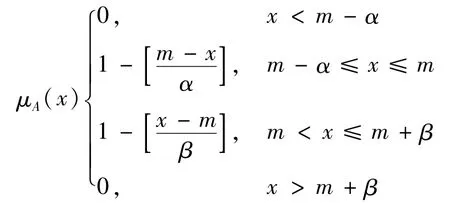
(3)模糊故障树。结合故障树分析方法及模糊集合论,形成模糊故障树分析方法,解决了实际应用中需要确定的故障频次的问题,能够更好地运用于实际生产中。
模糊故障树[(m-α),m,(m+β)]的λ(0≤λ≤1)截集
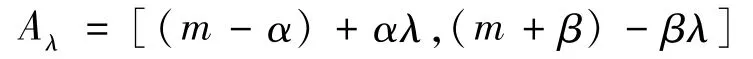
为一个区间数。设A、B为三角形模糊数,根据经典扩张原理,对于∀λ∈[0,1],有以下扩张运算式:
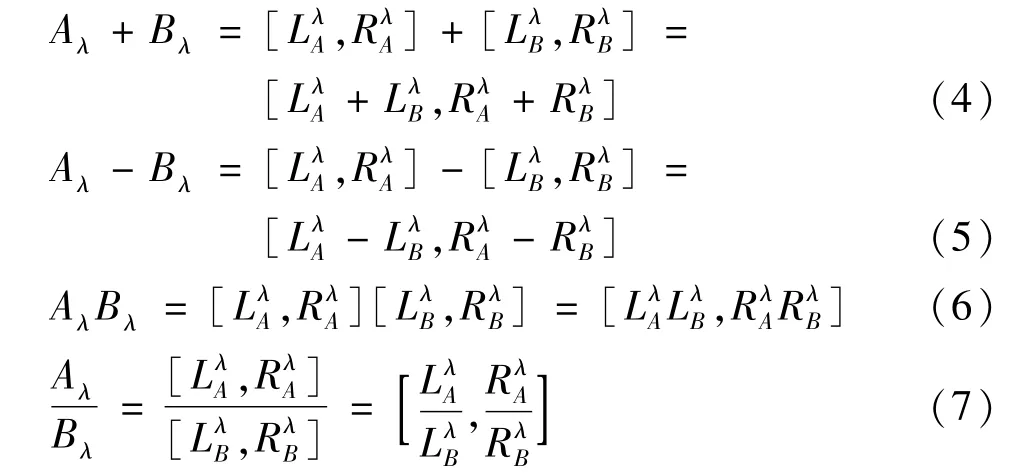
取三角模糊数的截集得到的区间数为基本事件的发生概率:
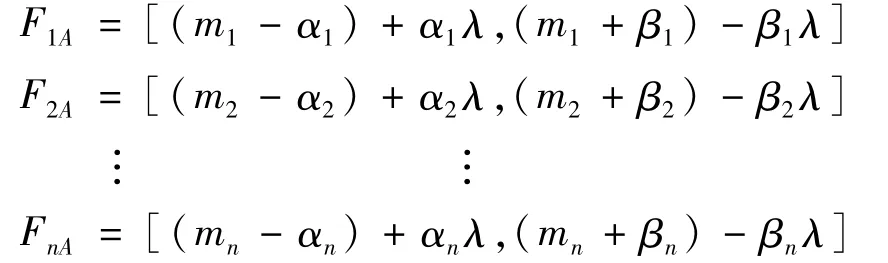
模糊故障树中,PT为顶事件T发生的概率,PTi为基本事件i对顶事件T的重要影响程度。PTi与PT的差值记为D。当D越大时,基本事件对顶事件T的重要影响程度也越大。
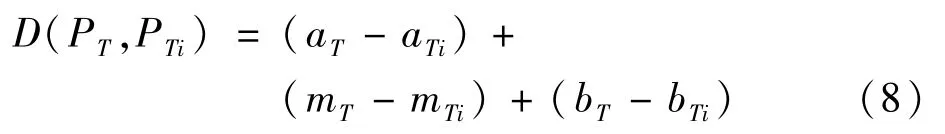
1.2 FMECA分析
假设某子系统以故障模式使机床发生故障不能正常运行的危害度为

子系统i对整个机床的危害度为
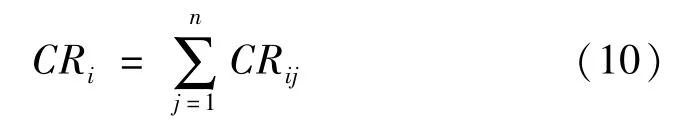
将式(9)代入式(10),得:
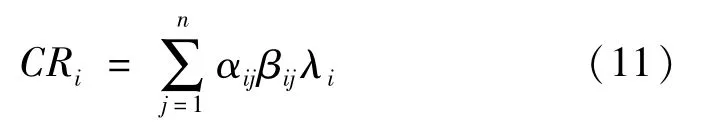
子系统i以故障模式j使机床发生故障不能正常运行的概率为

式中:n为子系统j出现故障模式的种类数;nj为第i个子系统第j种故障模式出现的次数;ni为子系统全部故障模式发生的总次数。βij为第i个子系统以第j种故障模式故障造成该子系统损伤的概率[14-15]。
国家标准:βij=1表示子系统肯定发生损伤;βij=0.5表示子系统可能发生损伤;βij=0.1表示子系统很少发生损伤;βij=0表示子系统不发生损伤无影响。
λi为子系统的基本事件故障率,平均故障率

式中:Ni为子系统在规定时间段内的故障的总次数;∑t为子系统在规定时间段内累计的工作时间。
2 案例分析
分析机床:某高端五轴联动数控机床。
采集数控机床近3 a实际故障数据,取故障频次2%以上故障部位进行具体分析。共取子系统9个,每一子系统细分具体故障部位,并采用模糊故障树及FMECA分析方法分析得出其模糊重要度、危害度等指标。再运用综合指数评价分析方法综合分析两大指标,得到分析结果。
2.1 模糊故障树的建立
依据某高端五轴联动数控机床数据绘制出其故障树,如图3所示。故障树中间事件及基本事件编号及所标含义如下:M1—自动交换系统;M2—主轴系统;M3—坐标轴系统;M4—激光检测系统;M5—气动系统;M6—精度;M7—CNC系统;M8—防护系统;M9—排屑系统;X1—位置检测;X2—链条;X3—换刀臂;X4—自动交换系统检测;X5—控制;X6—主轴检测;X7—冷却;X8—主轴电动机;X9—编码器;X10—传动连接部件;X11—坐标轴电动机;X12—导轨;X13—激光测刀;X14—探头;X15—气路;X16—定位精度;X17—原点偏移;X18—NC系统;X19—检测(安全门等);X20—防护罩(帘);X21—排屑电动机。

图3 某高端五轴联动数控机床故障树
由表1可以算得:

通过Fx1,Fx2,…,Fx21及式(4)~(7)可求得中间事件(各子系统)的模糊发生概率为:
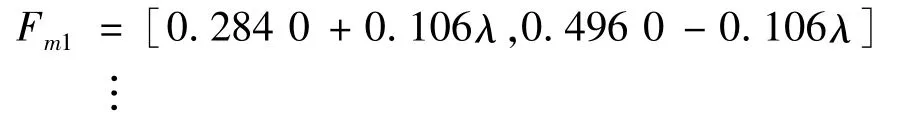

再通过Fm1、Fm2…Fm9及式(4)~(7)可求得顶事件的模糊发生概率为:
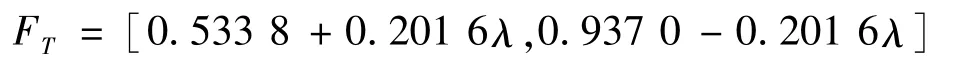
由计算可知:某高端五轴联动数控机床不能正常工作的概率为
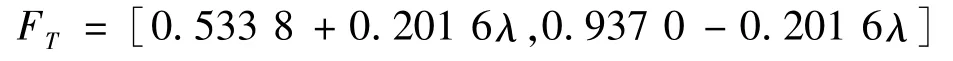
当λ=1时,底事件的发生概率为确定值,FT1=0.937 0;当λ=0时,FT0=0.533 8。总之,顶事件发生概率的最小值为0.533 8,最大值为0.937 0,且概率为0.735 4的可能性最大。
在完成对数控机床模糊故障树分析后,可根据模糊重要度方法计算出各故障重要度,以用于综合指数评价分析。
据式(8)可得出各基本事件模糊重要度如表2所示。
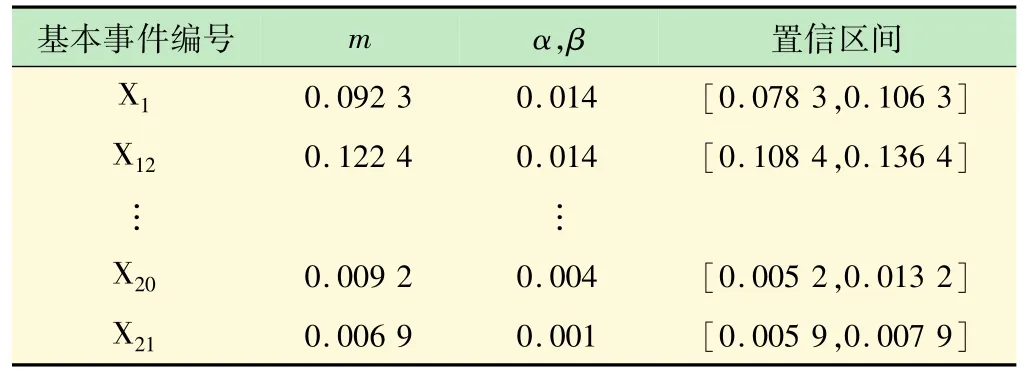
表1 故障事件及发生概率
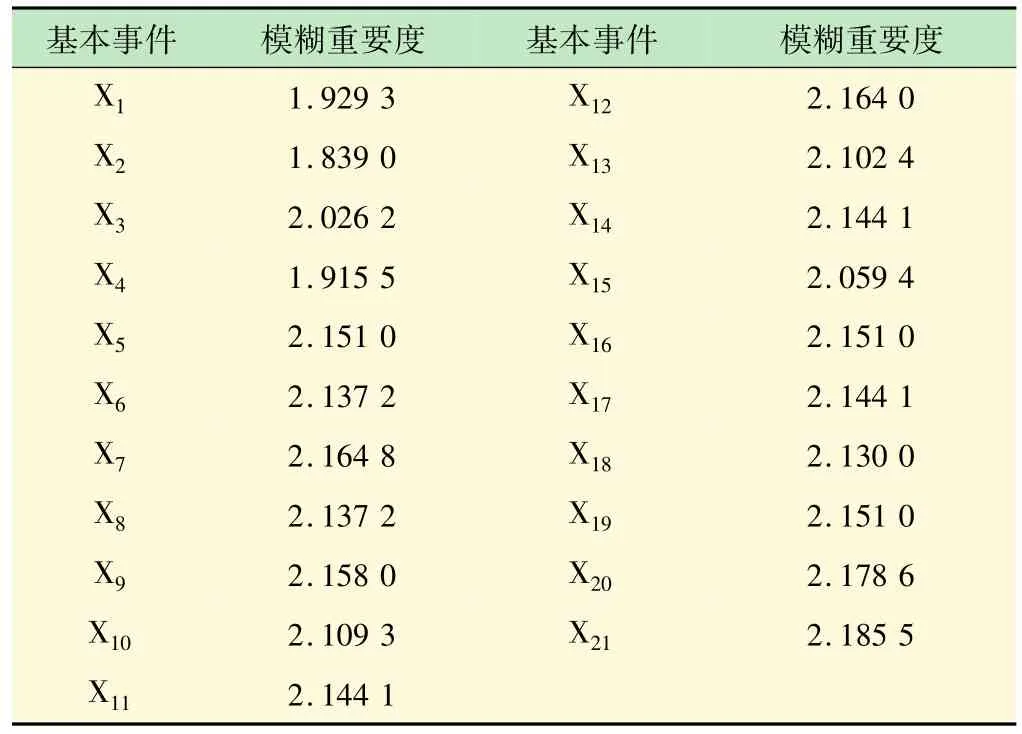
表2 各基本事件模糊重要度
2.2 FMECA分析
某五轴联动数控机床的工作月份为2013-01~2017-12,其累积工作时间为109 680 h,其中故障时间为3 634.172 5 h。
通过计算可得出该机床的累计工作时间为∑t=106 045.827 5 h。可计算出各个子系统的FMECA值,见表3。
2.3 综合指数评价分析
确定数控机床基本事件模糊重要度及危害度后,先进行归一化处理,得出其综合指数[16]。某高端五轴联动数控机床综合指数评价分析见表4所示。

表3 某高端五轴联动数控机床FMECA分析
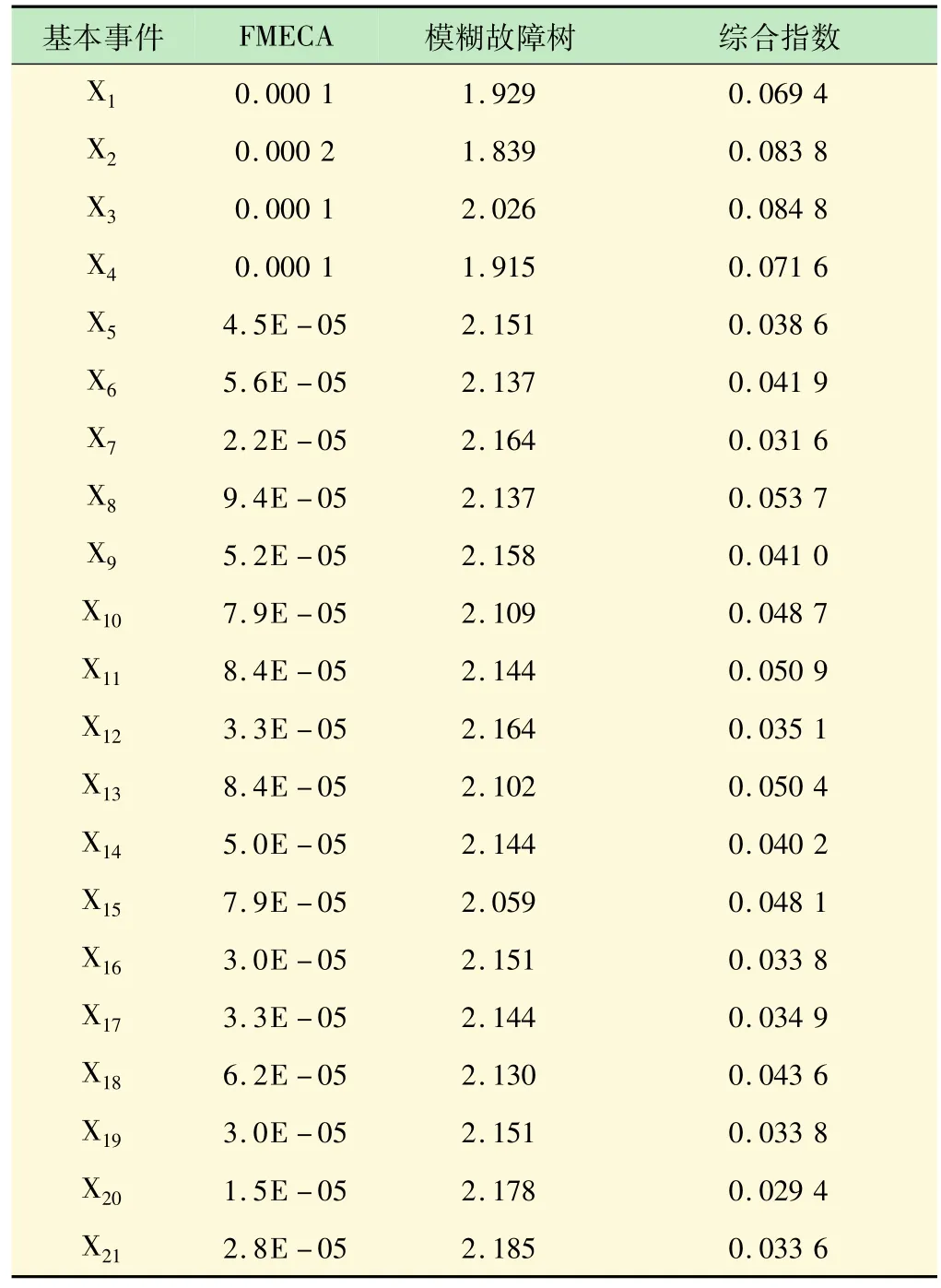
表4 综合指数评价分析表
得到各故障部位综合指数后,可根据故障树划分求得隶属子系统综合指数并进行排序。各子系统综合指数排序见表5。
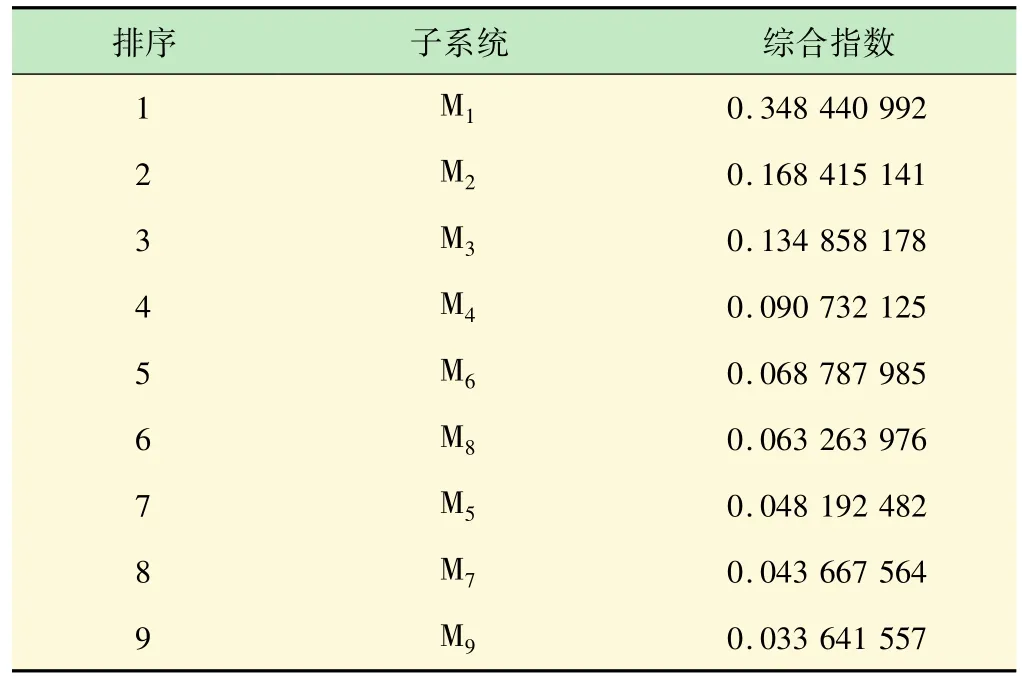
表5 各子系统综合指数排序
3 结 论
(1)基于模糊集合论及故障树分析方法,建立数控机床模糊故障树,对传统故障树进行优化,解决故障树在实际应用中无法获知准确故障数据的问题。
(2)依据模糊故障树分析方法得出的各故障模糊故障率,可为数字孪生车间及系统仿真的建立提供参考。
(3)运用基于模糊故障树和FMECA的数控机床综合评价方法比单一故障分析方法获取的结果更为准确、全面,从故障频次、重要度及危害度等多方面考虑,更符合数控机床系统复杂的特点。
(4)依据各故障的综合指数及排序,可为维护人员的日常维护保养提供参考。

