龙门铣床横梁结构的轻量化设计*

,2

1.陕西理工大学 机械工程学院 陕西汉中 723000 2.陕西省工业自动化重点实验室 陕西汉中 723000

1 轻量化设计背景

大型龙门铣床是飞机、轮船、汽车等工程领域广泛应用的一种机械装备。在实际应用过程中,滑鞍滑座和主轴箱的重力作用及横梁的自重作用,会使横梁产生较大的变形,进而可能会严重影响机床的加工精度。因此在传统设计中,龙门铣床横梁结构较为笨重,刚度冗余较大。减小横梁的质量,可以降低生产及安装的成本。如何在满足刚度要求的前提下减小横梁结构的质量,对大型龙门铣床的设计提出了新的要求。

目前,在国内外龙门铣床横梁结构研究中,主要采用优化横梁结构外形尺寸及内部筋板形状、尺寸、布局等方法,对横梁结构进行优化,达到轻量化的目的。茅启园等[1]通过对横梁结构进行静动态计算分析,得出横梁内部筋板振动是导致横梁结构加工精度不高的主要原因,并采用响应面优化的方法对横梁内部筋板的尺寸进行优化,提高了横梁结构的加工精度。程彬彬等[2]通过对横梁结构进行静动态分析,初步确定横梁结构优化的关键尺寸为横梁外壁厚与筋板厚度,通过灵敏度分析确定最终的设计变量,并通过响应面优化方法对横梁结构进行了优化。孙芹等[3]对横梁结构进行静动态分析,并利用拓扑优化的方法对横梁内部筋板进行重新布局,优化后横梁结构整体刚度得到明显提高,同时实现了轻量化。杨建交等[4]针对横梁截面尺寸较大导致质量过大的问题,通过正交试验、灵敏度分析等方法确定了横梁优化的关键尺寸,并采用响应面优化方法对横梁截面尺寸进行了优化。吴珊等[5]针对铣床加工刚度不足的问题,通过优化立柱内部筋板结构改善了立柱的静动态特性,从而使机床的加工精度和效率得到明显提高。Mu等[6]通过拓扑优化方法,将优化目标设置为横梁结构的整体最大刚度,在保证质量满足设计要求的前提下,对横梁结构进行优化,减小了横梁结构的变形。Zhao等[7]通过应用结构仿生学,研究大叶肋和仙人掌优良的结构与性能,将大叶肋和仙人掌结构特点应用于铣床横梁结构,使横梁结构的质量和变形减小。

上述研究虽然考虑了横梁结构的外形尺寸与内部筋板布局,但是忽略了横梁结构变化后固有频率的变化。笔者在龙门铣床横梁结构三维模型的基础上,利用有限元方法进行结构静力学分析,通过响应面优化方法,以横梁质量为目标函数,以最大变形和结构的一阶、二阶固有频率为约束条件,对横梁结构进行优化。

2 有限元建模

2.1 三维模型

根据龙门铣床横梁结构的设计尺寸,建立横梁结构的实体三维模型,如图1所示。横梁结构的外形尺寸为6 032 mm×1 315 mm×824 mm,横梁壁厚为20 mm,端面壁厚为30 mm,内部加强筋厚度为20 mm。横梁内部共有12条X形加强筋,横梁前端横截面为O形。横梁结构内部布局如图2所示。

图1 横梁结构实体三维模型

图2 横梁结构内部布局

横梁是薄壁件,横梁内部有12条X形加强筋、两个交叉板、两个上下横板,板上均有孔。横梁外部有许多倒圆、倒角、圆孔、小凸台等。可见,横梁结构较为复杂。在划分网格时,以上小特征内部会产生大量有限元单元,进而提高网格划分的难度。因此,在建模时对横梁结构进行简化[8]。

2.2 材料参数

龙门铣床横梁结构材料采用HT300灰铸铁,相关参数见表1。

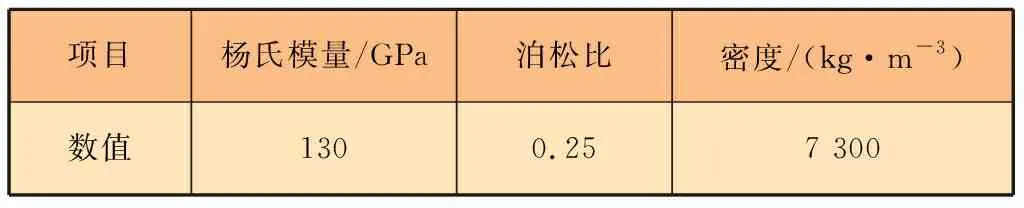
表1 HT300灰铸铁参数

2.3 网格划分

根据龙门铣床横梁结构特点,采用四面体法来划分网格。网格的单元数为384 017,网格的节点数为198 933,网格划分后模型如图3所示。

2.4 约束条件

由于横梁结构是通过两个立柱支撑的,因此在横梁与立柱接触的部位施加全约束边界条件。

2.5 载荷条件

横梁结构的受力情况主要来源于三个方面:横梁结构自重、滑鞍滑座及主轴箱的重力、切削力[9]。横梁结构的自重可以通过在整体结构上施加重力加速度来模拟,滑鞍滑座及主轴箱的重力根据实际情况,设置为40 000 N。

图3 横梁结构网格划分后模型

在实际切削加工时,如果采用圆柱铣刀,刀具材料为硬质合金,工件材料为灰铸铁,那么主切削力F为[10]:

(1)

式中:ae为铣削宽度,ae=90 mm;fz为每齿进给量,fz=0.16 mm/Z;ap为铣削深度,ap=8 mm;z为总齿数,z=10;d1为铣刀直径,d1=100 mm。

通过计算得到主切削力F为9 557 N,且Fy=0.76F=7 263 N,Fx=0.8F=7 647 N,Fz=0.36F=3 440 N。Fx为作用在龙门铣床主轴上的轴向力,Fy为沿竖直方向进给的分力,Fz为沿水平方向进给的分力,横梁结构受力分析如图4所示。

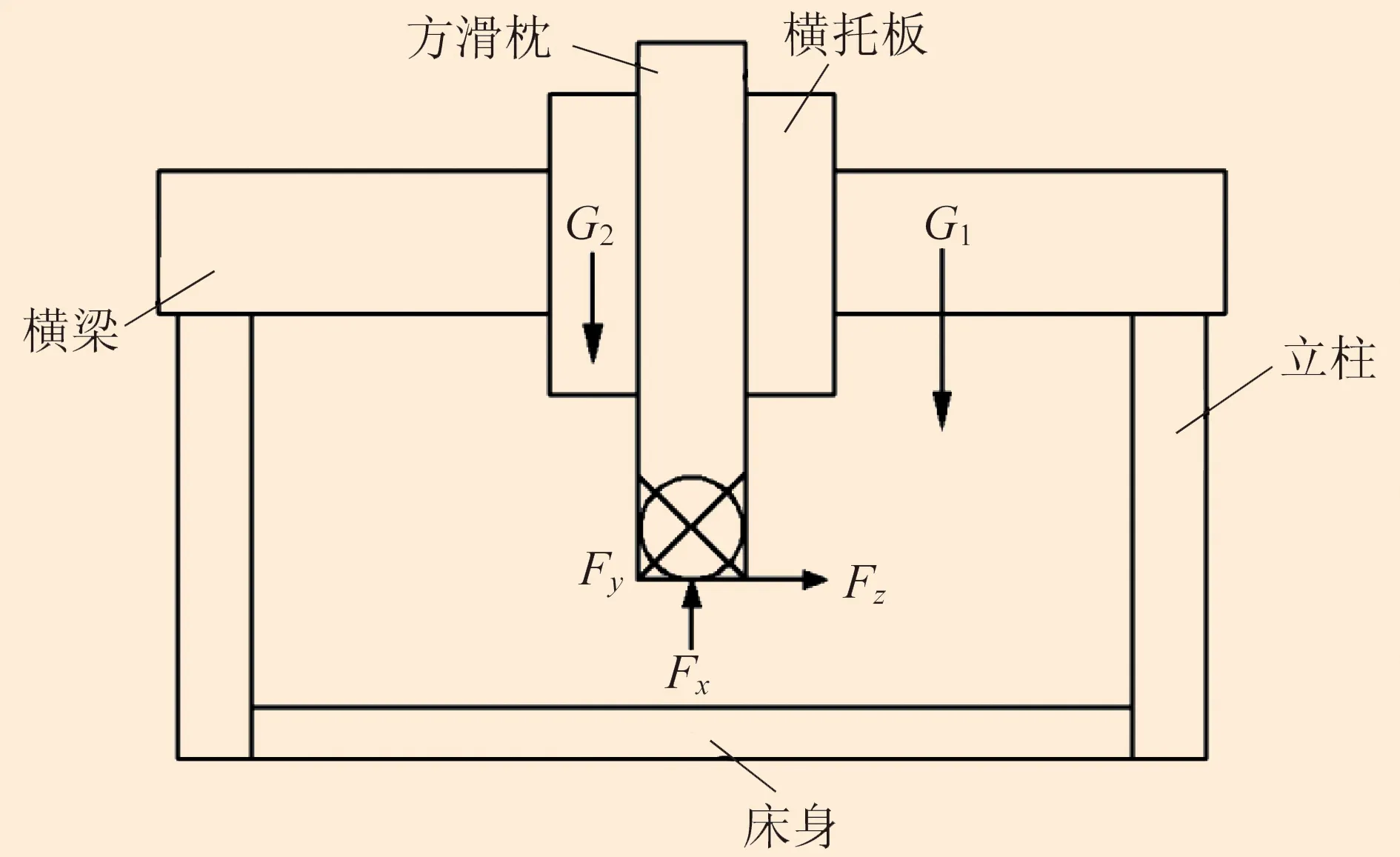
图4 横梁结构受力分析

横梁结构模型约束和载荷如图5所示。

图5 横梁结构约束和载荷

3 有限元分析

3.1 变形

经过有限元分析,横梁结构的整体变形云图如图6所示。

图6 横梁结构整体变形云图

在给定载荷下,横梁结构最大变形量见表2。

表2 横梁结构最大变形量

横梁结构中间部位最大变形量为0.026 mm,两端位置仅有向上翘起的轻微变形,因此横梁结构在刚度上有很大富余。可以通过优化横梁壁厚尺寸,来减小横梁结构的质量。

3.2 等效应力

横梁结构整体等效应力云图如图7所示。

图7 横梁结构整体等效应力云图

在给定载荷下,横梁结构最大等效应力见表3。

表3 横梁结构最大等效应力

横梁结构所受的最大等效应力远远小于材料的屈服应力250 MPa,因此并没有把结构抵抗破环的最大潜能发挥出来,设计过于保守。笔者对横梁结构进行轻量化设计,使结构的潜能充分发挥出来。

4 动态特性分析

4.1 理论基础

机床的动态特性可以通过模态分析得到,机床的振动主要由各个零部件的振动叠加而形成。横梁结构作为龙门铣床的重要部件,其结构对整个机床的加工精度有重要影响[11]。通过模态分析,研究横梁结构的振动特性,可以确认横梁结构的固有频率及振型。

系统的动力学方程为[12]:

(2)

在模态分析中,阻尼可以忽略不计,因此系统的动力学方程为:

(3)

在振动过程中,系统的自由振动为简谐振动,因此系统的位移函数为正弦函数:

Y=Asin(ωx)

(4)

式中:A为振幅;ω为系统的自振圆频率。

式(4)代入式(3),可得:

(-ω2[M]+[K]){A}=0

(5)

4.2 模态振型

横梁结构前两阶模态振型如图8所示。

横梁结构前两阶频率及振型特点见表4。

表4 横梁结构前两阶频率及振型特点

横梁结构的一阶固有频率为135.6 Hz。该龙门铣床主轴的最高转速为6 000 r/min,因此主轴激振频率的范围为0～100 Hz[13]。最大激振频率小于横梁结构一阶固有频率,即发生共振的概率很小。从振型来看,横梁结构主要发生弯曲和扭转振动,说

图8 横梁结构模态振型

明横梁壁厚对横梁刚度影响较大,故应通过优化尺寸来提高横梁刚度。

5 轻量化设计

5.1 灵敏度分析

灵敏度分析反映的是目标函数变化对设计变量变化的敏感程度,如果目标函数f可以用一个设计变量x或多个设计变量x1、x2、x3、…、xn来表示,那么灵敏度S可以用目标函数对设计变量的导数或偏导来表示,为[14-15]:

S=df(x)/dx

(6)

S=∂f(x1,x2,x3,…,xn)/∂xj

j=1,2,3,…,n

(7)

横梁结构内部较为复杂,尺寸较多,在选取最优设计参数时会存在一定的盲目性。通过灵敏度分析,可以计算出各个设计变量对目标函数的灵敏度值。根据灵敏度值的大小,能够很快确定出最优的设计参数。

优化中考虑到计算量及计算效率的均衡,选取20个横梁结构的尺寸作为设计变量。横梁结构的设计变量如图9所示,设计变量的取值范围见表5。

5.2 响应面优化

通过响应面优化,可以直接得到横梁结构各设计变量的灵敏度值,如图10所示。

横梁结构所有设计变量与横梁结构质量都成正相关,随着设计变量取值的增大,质量增大。其中,设计变量P16对横梁结构质量的灵敏度值很小,因此最终的输入变量剔除设计变量P16。

图9 横梁结构设计变量

表5 横梁结构设计变量取值范围

图10 横梁结构设计变量灵敏度值

响应面优化指根据试验设计方法对随机选取的一组试验设计变量进行试验,然后用多元二次方程来拟合各输入变量与响应之间的函数关系,通过二次多项式来表示响应面模型。响应值G为:

(8)

式中:a0为自由项因数;bi为一次项因数;cii为二次项因数;i代表设计变量。

通过对横梁结构的有限元分析计算,在保证横梁结构强度和刚度的前提下,以横梁结构质量最小为目标,建立响应面优化数学模型[16-17],为:

minfw(X)

(9)

5.3 优化结果分析

通过响应面优化对横梁进行轻量化设计,得到横梁结构整体变形云图、等效应力云图、前两阶模态振型,依次如图11、图12、图13所示。

轻量化设计前后横梁结构主要参数的对比见表6。

轻量化设计前,横梁结构的最大等效应力为6.197 9 MPa。轻量化设计后,最大等效应力减小为5.274 8 MPa,减小了0.923 1 MPa,表明横梁结构的刚性得到提高。轻量化设计前横梁结构最大变形量为0.026 mm,轻量化设计后最大变形量为0.025 8 mm,减小了0.000 2 mm,减小百分比为0.77%。轻量化设计前,横梁结构的质量为10 424 kg。轻量化设计后,横梁结构的质量为9 341.9 kg,减小了1 082.1 kg,减小百分比为10.38%。轻量化设计前,横梁结构一阶固有频率为135.6 Hz。轻量化设计后,一阶固有频率为141.41 Hz。一阶固有频率提高了5.81 Hz,提高百分比为4.28%。轻量化设计前,横梁结构二阶固有频率为142.33 Hz。轻量化设计后,二阶固有频率为148.8 Hz。二阶固有频率提高了6.47 Hz,提高百分比为4.54%。

图11 轻量化设计后横梁结构整体变形云图

图12 轻量化设计后横梁结构整体等效应力云图

图13 轻量化设计后横梁结构模态振型

表6 横梁结构主要参数对比

6 结束语

笔者对龙门铣床横梁结构进行了轻量化设计。在轻量化设计中,应用灵敏度分析方法,对设计变量进行了筛选,确定了优化参数。通过响应面优化方法,在横梁结构实体模型的基础上,以横梁结构质量最小为目标函数,以横梁结构等效应力、最大变形,以及一阶、二阶固有频率为约束条件,对横梁结构进行了优化。轻量化设计后的横梁结构,质量减小了10.38%,一阶固有频率提高了4.28%,二阶固有频率提高了4.54%,在轻量化设计的过程中兼顾了横梁结构的静态及动态性能。