基于并行计算的电力系统静态安全分析技术

朱启凌 周 越

国网上海市北供电公司

0 引言

高效的电力系统静态安全分析技术需要减少安全分析时间，提高安全分析精度。传统的串行计算方式此时便渐现颓态，因其工作原理的原因，其无论在计算速度还是在计算规模上已无法满足电力系统计算中对大电网计算的要求。因此针对静态安全分析精度和分析速度的研究是改良电力系统静态安全分析技术的关键。近年来，图形处理器（GPU）飞速发展，其由数以千计的更小、更高效的核心组成，这些核心专为同时处理多任务而设计。利用GPU进行的并行计算可以达到快速、高效的要求[1]。

2008年，NVIDIA公司推出了CUDA，作为一种全新的并行计算架构，它的推出是为了打通并行计算与串行计算之间的壁垒。CUDA的开发环境和软件体系以C/C++语法为基础设计，为其被广泛地使用奠定了基础。

1 CUDA编程模型

CUDA架构不同于之前的图形处理架构，其在实现数学逻辑单元时都确保他们满足IEEE单精度浮点数学运算的需求，并且其执行通用计算是依靠一个裁剪后的指令集[9]。GPU上的执行单元不仅可以任意地读/写内存，还能访问缓存（共享内存）。这些CUDA架构的功能都是为了让GPU在具备传统图形计算能力的基础上还能高效地执行通用计算[2]。

CUDA架构采用CPU+GPU的异构方式，将CPU作为主机，负责串行计算与事务处理，GPU作为设备或协处理器，负责执行高度线程化的并行处理任务。

在CUDA中执行并行任务的函数称为内核函数（kernel），每一个kernel函数中都含有两个层次的并行模型：Grid中的Block并行与Block中的Thread并行。CUDA线程结构如图1所示的方式组织，一个kernel就是一个大线程网格Grid，在其中还有许多的线程块即Block，而在线程块中便是kernel中最基本的数据并行执行单元线程Thread。同一线程块中的众多线程不仅能够并行执行，而且能够通过共享存储器（Shared memory）和栅栏（barrier）通信。这样，同一个大的线程网格内的Block是彼此不能通信但可以并行执行的单元，而同一个Block内的各线程之间形成的是允许通信的细粒度并行，这就是CUDA的双层线程模型[3]。

CUDA采用的是单指令多线程（SIMT）的执行模型。每个流处理器(执行单元)对应一个线程,每个流多处理器（处理核心）对应一个或几个线程块。执行时，每发出一条指令，SIMT单元都会选择已经准备好的线程，若指令需要等待时，会自动切换到其他线程，从而隐藏线程延迟和等待达到并行化[5]。

在CUDA中，GPU不能直接存取主存，只能存取显卡上的显卡内存[7]。因此,需要将数据从主内存先复制到显卡内存中，进行运算后，再将结果从显卡内存中复制到主内存中。

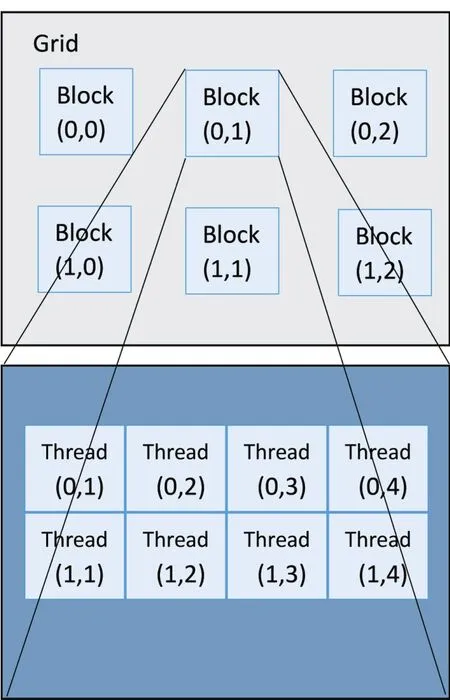
图1 线程结构图

2 并行算法实现

电力系统主要以N-1校验的方式进行安全分析，即：在系统运行状态下，断开任意一条线路后判断电力系统各项运行指标是否满足要求。由于需要对全部线路进行N次计算分析，因此，计算量很大。

现在的静态安全分析采取的是一种预判方法，对系统进行多次潮流计算后，筛选出可能会引起电压越限和功率过载等问题。针对计算结果进行静态安全的分析，判断系统是否能够安全运行[4]。

本文主要针对潮流计算算法的并行化，通过并行化处理，加速潮流算法的计算，从而大幅节省了时间，加快了静态安全分析的速度[8]。

2.1 牛拉法解潮流及其并行化实现

首先要理解牛顿迭代法：

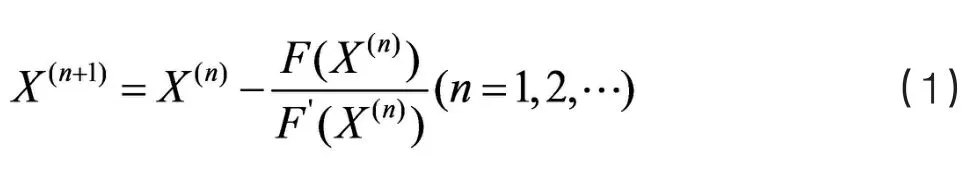
根据功率方程，可分为有功功率方程与无功功率方程，从而可确定4个变量，分别为：节点注入有功，节点注入无功，节点电压，节点相位角。根据各个节点的不同特点，可分为三类：PQ节点，PV节点和平衡节点。

利用直角坐标表示电压和导纳，将其代入节点电压方程，整理后可得出修正方程：

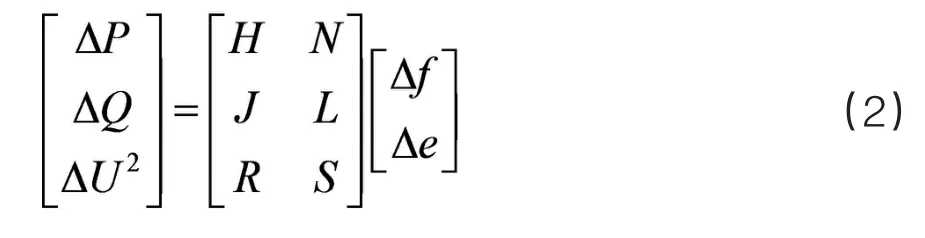
为了解潮流，需要将电力系统各节点的原始数据和信息转换为节点导纳矩阵，再代入初值进行计算，不断进行迭代直到收敛。

为了将算法并行化需要进行分类，牛拉法中存在迭代的部分分别是形成导纳矩阵、雅克比矩阵和求解修正方程。这两部分都需要累加计算来完成，可以将任务分解，之后分配给线程并行执行。这需要在迭代开始之前编写相应的语句。

针对导纳矩阵的形成，为了方便任务的分解，将各节点进行编号，并将编号的数据存储在两个数组内，通过这两个起点和终点数组来确定支路，同时还需要将支路的等效导纳存储进一个数组。当程序运行时，首先需要获取当前线程的索引。再通过循环迭代，每个线程负责一条支路信息的形成，从而达到并行。由于导纳矩阵的形成并不复杂，这一部分的并行化并不会优化很明显。

针对牛拉法解潮流，还需要进行并行化处理的是雅克比矩阵的形成。在这部分程序中，与导纳矩阵的形成类似，需将雅克比矩阵中各个分量进行循环计算即可，即：用线程负责矩阵各个块内的各个元素，当然还需注意每个块内的计算公式不同。

最后，针对算法中计算量最大的解线性方程组部分，利用QR分解法进行单独分析。

2.2 QR分解法解线性方程组

QR分解定理是对于任意非奇异矩阵A∈Rn×n，存在正交分解：

其中，Q为n阶正交矩阵，R为非奇异的上三角矩阵。此分解的唯一性限定条件是R的对角线元素为正数[6]。

针对此方法，采用基于Householder方法和基于Givens方法进行并行化实现。

2.2.1 基于Householder的分解算法

第一种方法是基于Householder变换的QR分解，若我们待求的方程称为Ax=b，其原理就是将矩阵A的第一列拿出构造Householder矩阵，将Householder矩阵与矩阵A相乘得到一个新的矩阵，然后再将的第二列拿出构造，并变换得到。

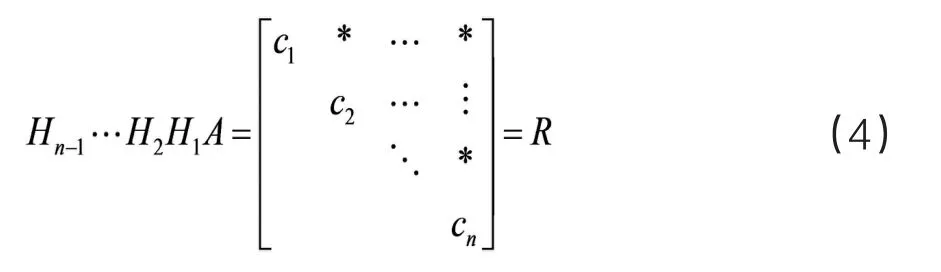
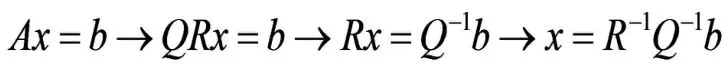
针对此方法，同样采用分配线程的数据并行化方法，为矩阵构造Householder矩阵来构造原矩阵的上三角矩阵。

利用以上代码做好变化，分配好显存空间与线程数量，利用数据并行进行运行从而达到并行加速效果。

2.2.2 基于Givens的分解算法

基于Givens算法更清晰的阐释了双层并行模式，用线程结构而言，即同一Block中的线程可以同时进行操作的数据并行和多个Block的数据可以同时进行操作的任务并行。而将其运用到算法中就是当对非奇异矩阵G进行处理时，需要得到上三角矩阵R。数据的处理顺序是：先对第一列中最低行元素进行置零操作，对相邻两行的元素先完成Givens的计算和变换。当一列操作完成后再进行下一列操作，而在程序进行时，各行之间的数据是独立存在的，这便是数据级并行。任务级并行便是程序运行时各列之间是相互独立的，比如在计算第二列元素时，后面的元素便不再依赖第二列以前的元素。

在程序代码中，对负责Givens矩阵变换的Kernel进行调用。调用之前，需要先定义初始矩阵存储数据并且还要定义任务数，一个大小为的矩阵，需要m-1个任务。

对于kernel函数Kernel_GQR：首先对任务进行顺序处理即计算该任务对应的两行的Givens矩阵的参数，再根据计算出来的矩阵参数和类型，更新相应的数据，此处的数据更新用到的便是数据级并行的概念，一个线程完成一个元素更新的工作。完成最后工作需要调用Kernel_GQR函数，对于上述所说矩阵，需要调用m+n-2次便可以完成整个变换过程。在调用循环的最后，需要更新该任务的运行次数，从而重新启动Kernel_GQR防止出现因没有数据全局同步而造成的竞争。

整个程序中，每个Block作为上述所说Task负责相邻两行的变换工作，为任务级并行单位，而存在于Block中的Thread负责每个矩阵元素的变换工作，为数据级并行单位，从而充分体现了GPU计算的特点。

3 实验结果

3.1 实验环境

本文在windows 7操作系统中的visual studio 2013上运行基于GPU的CUDA编程架构。针对整个静态安全分析待处理数据，利用并行化程序进行处理。而并行化的主要部分是潮流计算的加速，针对其中被分为三部分的并行部分进行分别处理。为了体现GPU并行计算的优异计算性能，采用CPU与GPU算法的运行时间结果分析。针对其加速比，采用四个算例IEEE30、118、300、2 383进行继续对比。

3.2 实验结果

本次实验计算雅克比矩阵时仅保留泰勒级数的一次项，计算精度为。详见表1～表3。

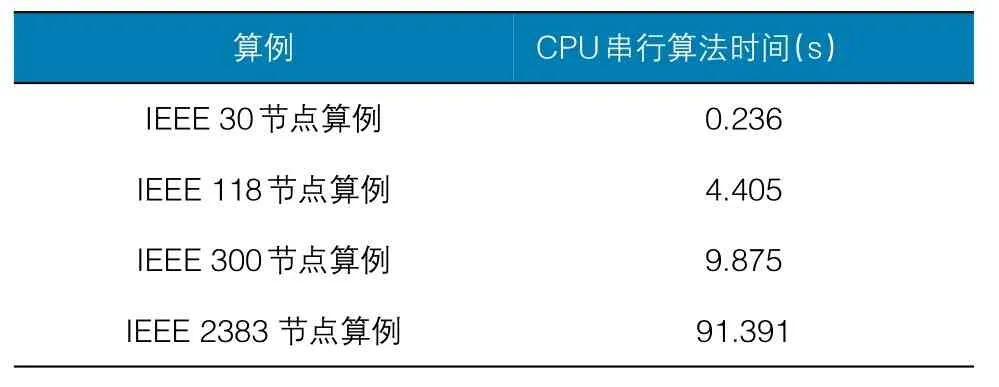
表1 CPU算法运行时间

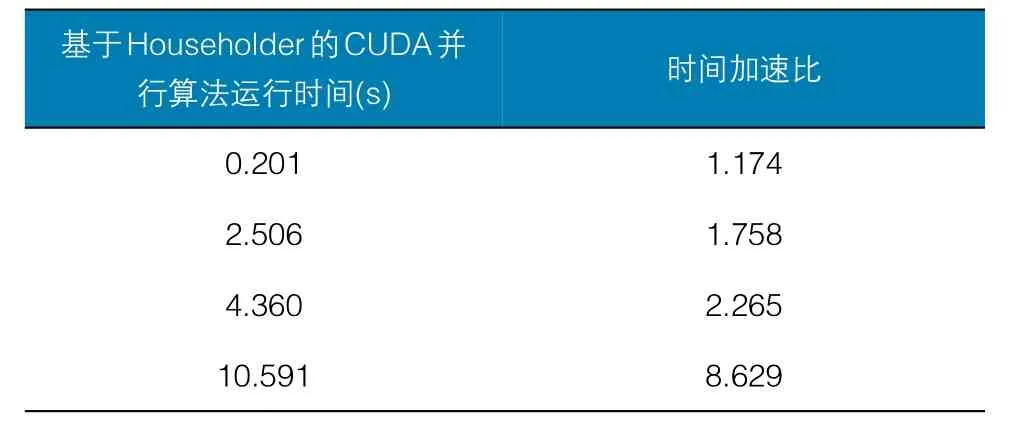
表2 基于Householder的算法时间与加速比

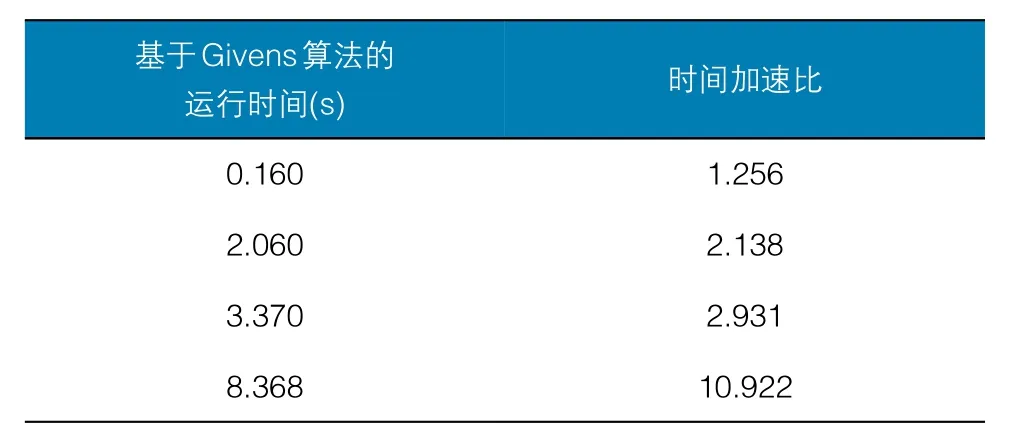
表3 基于Givens的算法时间与加速比

根据数据对比图可直观的感受到加速效果。

由图2和图3可见，基于GPU的并行算法对于整体的分析程序确实有着一定加速的能力，当数据规模越大，其利用的GPU数据并行越能掩盖线程延迟从而达到好的加速效果。同时，由于基于Givens算法还采用了任务并行的概念，减少了计算步骤，从而有着更优异的性能。

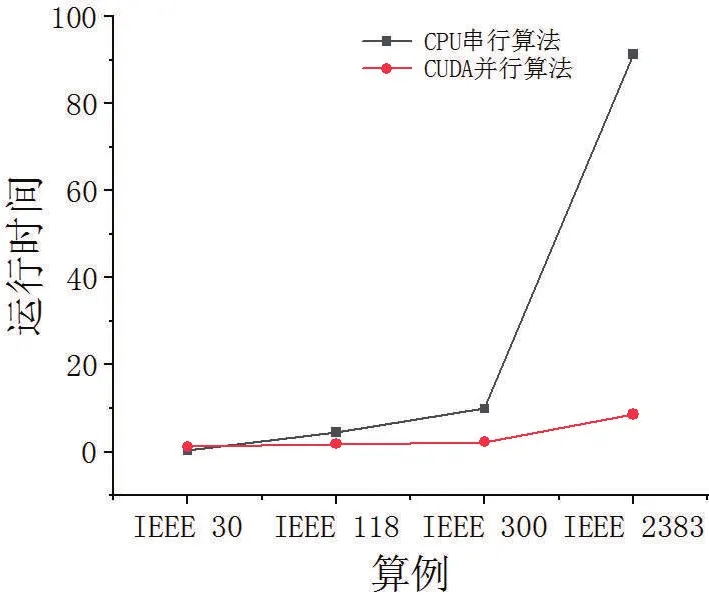
图2 CPU算法与GPU算法运行时间对比图

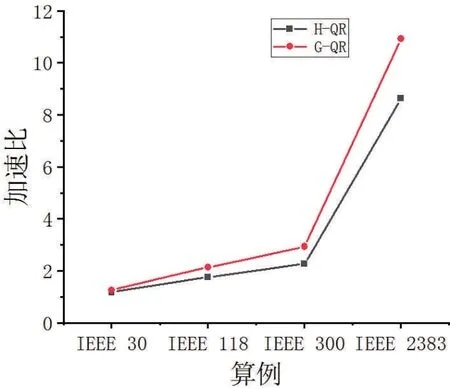
图3 基于Householder算法与基于Givens算法的加速性能对比图

4 结论

本文通过介绍基于GPU的CUDA架构，以牛拉法潮流计算将并行计算技术应用于电力系统静态安全分析中，在一定比例上提高了计算速度。潮流算法的计算量主要集中于解方程组，着重分析所采用的QR分解来求解算法。利用CUDA的线程结构的特点，达到数据并行和任务并行，从而提高了程序处理速度。

但是，其对于这些数据的处理方式基本相同，对于并行数据量越大、数据越密集的情况，并行效果越好，这一点与电力系统具有稀疏的电网结构相违背。因此，若使CUDA技术在电力系统中发挥其强大的计算能力,必须要开发出适合GPU这一结构的新算法。