基于北斗系统的多基地声呐浮标阵对潜定位性能研究

李沛宗，鞠建波，周 烨，李启飞，郁红波

(海军航空大学， 山东 烟台 264000)

卫星除了可以采用单点定位的方式对目标进行定位外，还可以使用差分定位的方式进一步提高定位性能。差分定位使用一确定位置基站的卫星坐标读数修正待测目标位置读数，以减少公共误差量，从而达到提升精度的目的，实现原理较为简单，效果显著，在军事领域具有巨大的价值。目前采取北斗差分定位，在车辆导航、飞机导航、舰船导航以及导弹制导领域都有一定研究。但对于航空反潜领域差分定位的相关研究还相对较少，对新型数字浮标进行北斗差分定位相关研究及应用具有很大价值。

多基地声呐系统由若干主被动声呐联合组成，能在浮标一定的前提下提高覆盖面积，同时技术实现相对而言较为简单，隐蔽性较好不易被潜艇发现并规避，是目前反潜战术研究的一个重点。使用声呐浮标阵对潜艇进行定位传统算法包括：HYFIX法、LOFIX法、以及利用目标多普勒信息的Doppler-CPA法。文献[3-6]对这3种方法已有详细论述，其结果表明使用传统算法结合浮标位置信息虽然可以对目标进行定位，但由于其对不同接收端收到的信息利用率较低，导致定位精度较差。针对传统定位算法的不足，文献[7-8]基于最小二乘法对浮标阵定位问题进行了分析，效果明显优于传统算法，但由于最小二乘法的局限性，其针对浮标阵定位问题的求解实际上是有偏差的，并不是最优估计。文献[9-10]提出了采取总体最小二乘对浮标定位进行解算的方法，但仍然存在模型过于简单、对误差要素分析不足的问题。

考虑到以上问题，参考以往文献的研究成果，本文以主动全向浮标与多枚被动全向浮标组成T-RN(由单个主动浮标与若干被动浮标组成)多基地浮标阵为例，结合北斗卫星对浮标位置的单点定位与差分定位，利用WTLS(加权总体最小二乘)算法，对多基地浮标阵对目标的定位误差进行仿真分析。

1 多基地声呐定位模型

当声呐的作用距离远远大于目标深度时，目标深度对定位误差影响较小，在二维平面上对定位误差进行分析即可取得与实际相近的结果。本文也将建立在二维平面上基于各浮标接收到信号的时间差对定位误差进行讨论。多基地系统对潜艇定位的模型如图1所示。

图1中，T为主动浮标，其发射声波被潜艇目标Sub散射后可被T本身与S1，S2等被动浮标接收。在多基地系统中，各个浮标阵元通过数据链实现时间同步，通过读取T发射声波的时间与各阵元接收到回波的时间即可实现对潜艇目标的定位。以T发射声波的时刻作为0时刻，T接收到回波的时刻为t0，各个被动浮标接收信号时刻分别为t1、t2、…，以此类推。潜艇到达各个阵元的距离分别为R0、R1、R2、…。潜艇位置坐标(x,y)，主动浮标T位置为(x0,y0)，各个被动浮标位置分别为(x1,y1)、(x2,y2)、…。构建方程如下：

(1)

图1 多基地声呐系统对潜定位模型示意图

对方程(1)进行变换，有：

可以由信息中心牵头组织，通过举办讲座、印发手册及网络宣传等手段，对全校的师生进行网络安全的教育，弘扬正能量，增强了师生的网络安全意识，有助于他们养成良好的上网习惯，自觉主动地营造好的环境，可以在上网过程中，人为消除一些不必要的隐患。

2(x0-xi)x+ 2(y0-yi)y=ti(ti-t0)·

(2)

改写成矩阵形式，有：

(3)

式(3)中，N为被动浮标的数量。其矩阵具有如下形式：

A·α=β

(4)

通过观察可以发现，当被动浮标大于3个时所求解的方程组为超定方程组，且由于观测误差的客观存在，按照方程解算求解只能解出一个区域，极端情况下甚至是无解的。为避免这一问题，可采用最小二乘法对目标潜艇位置向量α进行估计，经典的最小二乘解法下得到得到α向量的估计值为：

(5)

2 多基地浮标阵系统误差分析与目标位置解算方法

将式(4)改写为如下形式：

(Ar+ΔA)·α=(βr+Δβ)

(6)

式(6)中，Ar、βr由真实值构成；矩阵ΔA、Δβ由观测误差构成。对于低速航行的潜艇目标可忽略由潜艇运动导致的误差而只考虑观测误差[5]，则观测误差主要来源于浮标位置误差以及浮标对回波信号到达时间的测量误差。首先将误差写成3个N+1维向量形式，ΔX、ΔY、ΔT，分别表示各个浮标位置的x方向误差、y方向误差以及浮标接收信号时间的测量误差。分析ΔA，由于A的线性性，ΔA矩阵具有如下形式：

(7)

对其进行改写，使用误差向量表示，有：

(8)

分析Δβ，通过观察表达式不容易直接分离出Δβ，故从β矩阵本身出发，将误差的3个来源代入式(5)中的β，其元素可以写成如下形式：

(ti+Δti)2·c2-(ti+Δti)(t0+Δt0)·c2+(x0+Δx0)2+

(y0+Δy0)2-(xi+Δxi)2-(yi+Δyi)2

(9)

化简并忽略误差二次项带来的影响，分离其中所有带微分的量得到Δβ中的元素形式为：

(2tiΔti-t0Δti-tiΔt0)·c2+2x0Δx0+

2y0Δy0-2xiΔxi-2yiΔyi

(10)

改写成向量形式，有：

(11)

由于A与β中均存在由观测导致的误差，根据最小二乘理论[11]，采用式(5)的方式对目标位置进行估计，实际上并不是关于潜艇位置的无偏估计，相当于增加了误差来源项。因此为了避免求解计算的有偏性，导致不必要的误差项存在，采用WTLS算法对目标位置进行无偏估计。首先构建平差准则：

(12)

式(12)中：e为[Δβver(ΔA)]，ver函数表示对矩阵按列拉直运算；W为权系数矩阵；Q矩阵代表协因数矩阵；W、Q互为逆矩阵。协因数矩阵Q可以通过结合ΔX、ΔY、ΔT中元素的概率分布参数与ΔA、Δβ的结构进行构建，具体方法不做赘述。

WTLS算法实际上是求解平差准则式(12)在式(6)条件下的条件极值，本文采用拉格朗日数乘法进行求解，在求解过程中构建拉格朗日函数：

Φ=eTWe+2λT(βr-ΔA·α-Ar·α+Δβ)

(13)

3 仿真计算与分析

仿真1:仿真阵元个数改变对给浮标阵定位误差带来的影响。

分别仿真北斗卫星单点定位与差分定位条件下的T-R3，T-R4，T-R6多基地系统对目标的定位误差，卫星对浮标进行单点定位一般是通过浮标中的卫星模块接收卫星信号结合卫星星历与时钟对浮标直接进行定位，目前新升空的北斗三号卫星对亚太地区离岸100 km以上海域目标单点定位精度可以达到10 m以内，100 km以内区域可以达到5 m以内。其主要误差来源如表1所示，包括空间误差、传播路径误差以及用户接收端误差。

表1 不同误差源对北斗卫星单点定位的影响

卫星差分定位的原理是根据两接收站间空间传播误差与传播路径误差等公共误差的相关性，利用卫星对一坐标位置确定的基准站的定位读数修正卫星对未知目标的定位读数，以达到降低公共误差提高对未知目标定位精确性的目的。根据表1，假设北斗卫星对浮标单点定位精度为10 m，差分定位精度1 m。以主动浮标作为坐标原点，被动浮标分别呈正三角形，正方形与正六边形均匀分散在主动浮标附近。需要注意的是，本文中的仿真只是以此浮标阵作为例子进行分析，实际使用中多基地浮标阵可以根据潜艇概略位置等因素改变阵元位置，从而使某一区域或某一角度具有局部优势作用范围，并且本文所分析的结果也可以较为容易推广到其他阵型的浮标阵中。各被动浮标与主动浮标距离均为1 km，海况条件良好，浮标发射天线垂直无晃动，各浮标对回波信号到达的时间测量的误差均为0.05s。潜艇处于低速航行状态，考虑到主动浮标在三级海况下作用范围普遍在8 km以上，结合以往对于多基地系统作用面积的相关研究。将仿真区域设置为8 km×8 km的正方形区域，区域内每隔0.1 km取一点进行仿真，每点仿真10 000次，得到仿真区域内浮标阵对目标的定位误差随目标位置变化，平均定位误差与最大定位误差分别如图2～图4所示。

图2 不同阵元个数下的定位误差等高线图

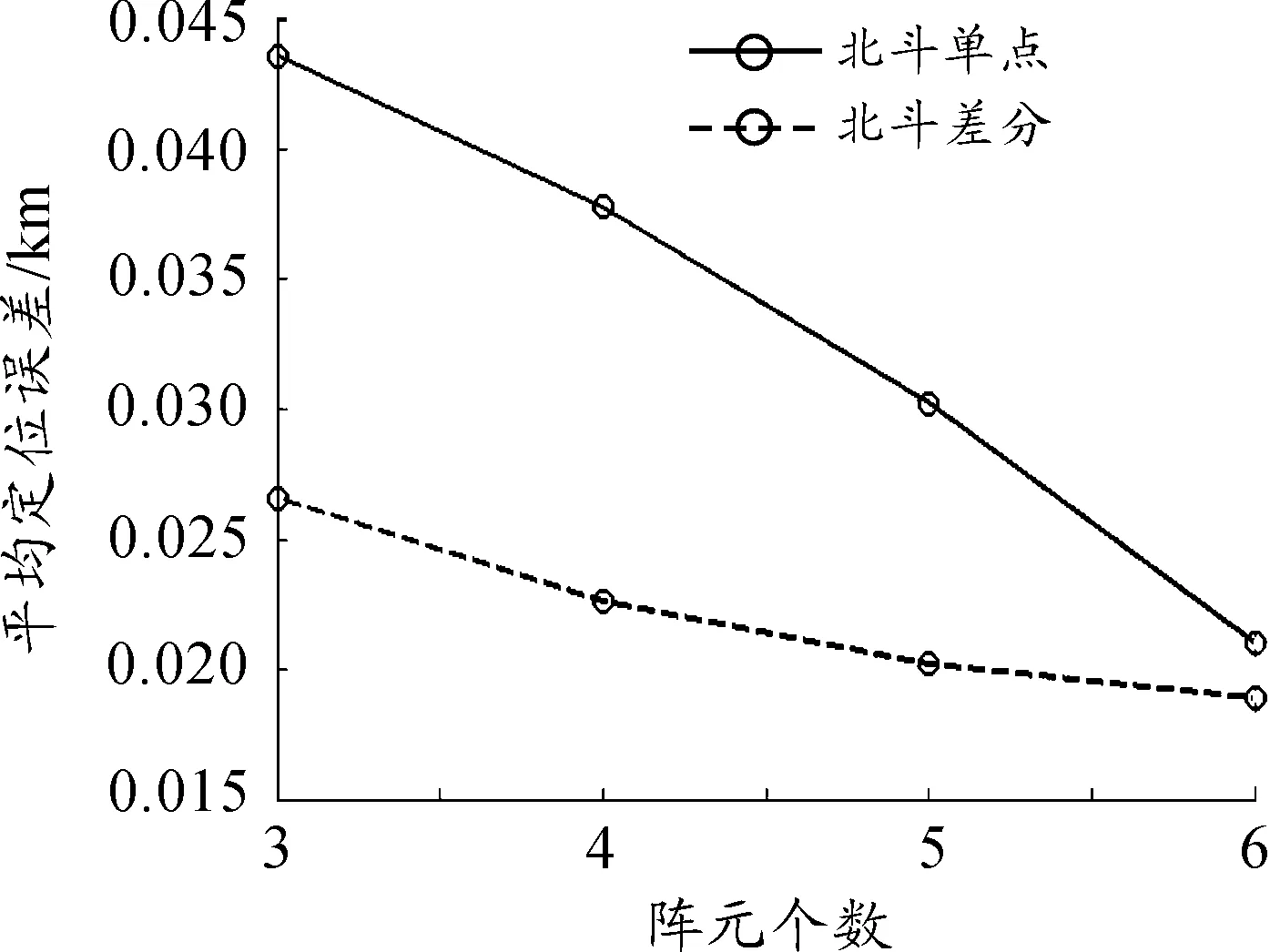
图3 仿真区域内平均定位误差随被动浮标阵元数变化曲线

图4 仿真区域内最大定位误差随被动浮标阵元数变化曲线

目标在仿真区域内距离浮标阵中心越远，定位误差越大，定位精度越差。目标越靠近多基地基线，则定位误差越大，浮标阵中心的主动声呐浮标附近定位效果最差。相同仿真条件下，采用北斗差分定位法，对浮标定位的浮标阵无论是平均误差还是最大误差都低于采用北斗单点定位的浮标阵。随着阵元个数的增加，平均误差与最大误差都会相应下降，但单点定位条件下的下降趋势明显高于差分定位条件，当被动浮标个数达到6个时二者在数值上基本相同。

使用浮标阵对水下目标进行定位时，不但要求定位误差尽可能小，而且希望在浮标阵有效区域内定位误差随目标位置的变化尽可能小，即定位的稳定性尽可能高，稳定性越高越有利于进行进一步的跟踪。定义目标区域的定位稳定性参数K为：

(14)

随阵元个数变化浮标阵定位的稳定性参数变化如图5所示。

图5中可以看出阵元个数越多，定位稳定性越好，北斗差分条件下的浮标阵定位稳定性远远高于北斗单点定位下的浮标阵。

图5 浮标阵定位稳定性随阵元个数的变化曲线

仿真2:仿真浮标测量回波信号到达时间误差对浮标阵定位性能的影响，以T-R3浮标阵为例，其他条件不变，由0.01到0.1连续改变时间测量误差，每隔0.01 s进行一次仿真，得到平均误差与定位稳定性如图6～图7所示。

图6 浮标阵平均定位误差随时间测量误差的变化曲线

图7 浮标阵定位稳定性随时间测量误差的变化曲线

由仿真结果可以发现，时间测量误差对浮标阵定位效果是一个较强的影响因素，仿真条件下时间测量误差每增大0.01 s，会给整体定位误差带来8 m到10 m的影响。改进浮标，使其对测量信号到达时间的测量更为精确，可以极大地提高浮标定位精度与稳定性。

4 结论

基于WTLS算法从精度与稳定性两方面对北斗卫星定位系统下的主被动全向浮标阵对潜定位进行了仿真。定义了一种反应定位稳定程度的稳定性参数，详细分析了主要误差来源改变给浮标阵对目标定位效果带来的影响。结果表明，采用卫星差分定位对浮标位置进行定位，提高浮标阵阵元个数与减小浮标测量回波信号到达时间误差均可以有效提升浮标阵定位精度，增强定位稳定性。本研究是以二维平面上的型多基地浮标阵为例，其结论可以拓展到三维与其他类型的浮标阵。