大数据时代应用统计学专业《数理统计》课程教学的探索与研究

潘保国

摘  要：《数理统计》是应用统计学专业重要的专业基础课，文章分析了应用统计学专业《数理统计》课程的教学现状，探讨和研究了教学内容、教学方法、教学手段和考核方式，为该课程的教学提供有价值的参考，提高了大数据时代统计学人才的培养质量。

关键词：数理统计;教学内容;教学方法;统计软件

中图分类号：G642       文献标志码：A         文章编号：2096-000X（2020）19-0027-04

Abstract： Mathematical Statistics is an important professional basic course for applied statistics majors. This paper analyzes the present situation about Mathematical Statistics course for applied statistical majors， discusses and studies the teaching content， teaching method， teaching means and examination mode， in order to provide valuable reference for this course teaching so as to improves the quality of statistics professional training in the era of big data.

Keywords： Mathematical Statistics; teaching content; teaching method; statistical software

随着微博、微信、QQ、朋友圈等社交网络的逐渐成熟，5G时代的到来，云计算和物联网技术的兴起，产生海量的多源异构的庞大数据流，数据量呈现爆炸式的增长，并超越了相应存储仓库和数据处理资源的发展，大数据时代已经来临。大数据具有如下五个基本特征：1.数据量大（Volume），数量级可达到ZB级别;2.输入和处理速度快（Velocity）;3.数据多样性（Variety），数据的类型不仅包括结构化数据，也包括半结构化、非结构化以及结构复杂的数据;4.价值密度低（Value）;5.数据准确性（Veracity）。大数据广泛应用于教育、医疗、交通和金融等行业。

大数据分析是计算机、数学和统计学等学科的交叉领域，拥有数据分析能力的统计学人才在电子商务、交通物流、产品开发以及营销等方面将发挥很大的作用，政府与企业部门对数据分析相关人才的需求也越来越大，尤其需要具有数据分析、数据挖掘能力的复合型人才。

《数理统计》课程是应用统计学专业的专业基础必修课程，是该专业的核心课程，并且是学位课程。它以《概率论》和《高等数学》为基础，是一门研究随机影响数据的学科，对随机影响数据进行收集、处理和统计分析，从而揭示与数据相关的总体特征和实物内部真正的统计规律，进行正确的预测和控制。目前，数理统计已广泛应用到工业、农业、经济、医学和生物等很多領域，成为诸如大数据和人工智能等新兴学科的理论基础。

《数理统计》课程教学存在教材内容侧重于理论，部分章节内容较难、公式繁多难记，考核方式单一等特点，这些显然不利于培养应用型人才。在培养应用型人才的背景下，需要加强理论联系实际，注重培养学生的应用能力和创新能力。为了激发学生学习兴趣，提高《数理统计》课程教学的教学质量和教学效果，提高学生的数据分析能力，以适应大数据时代的需求。下面，笔者结合当前应用统计学专业《数理统计》课程的教学现状，从教学内容、教学方法和教学手段等方面进行积极的探索与研究。

一、应用统计学专业《数理统计》课程的教学现状

应用统计学专业《数理统计》课程所使用的教材，一般采用茆诗松、程依明和濮晓龙编著的《概率论和数理统计》教材的下部分数理统计内容，或者采用茆诗松，吕晓玲编著的《数理统计学》。这两种教材都偏重于理论，缺少对统计软件实际操作的教学和指导，其中一小部分内容较难，学生不易理解，且存在少量与应用统计学专业《统计学》课程内容相重复的情况;教师注重理论的严谨性，重点放在定理的推导和习题的演算上，培养学生的实践能力不够，此种情况下，学生容易产生畏难情绪，该门课程的学习效果必将大打折扣;一些老师在教授《数理统计》课程时，教学方式单一，采取“灌输式”教学，担心自己的授课内容讲授不完，只顾赶进度，满堂灌，或者过多地依赖多媒体教学，很少板书;《数理统计》课程的传统考核方式仍以闭卷考试为主，其中期末成绩占 70%，平时成绩占 30%，或者期末成绩占 60%，期中成绩占 20%，平时成绩占 20%，这种传统的考核方式主要是考核学生对课本知识的掌握程度，强调对理论知识的考查，对复杂计算题和实际应用题考核不够，忽视了对该课程应用部分的考查。

二、根据应用统计学专业人才培养方案，优化教学内容

为培养应用型人才，教师在教学过程中，应淡化证明，突出应用，既要注重数理统计的基本概念、基本理论和基本方法的讲解，又要加强教学内容与实际应用的有机结合，以培养学生应用统计知识和统计方法解决具体实际问题的能力。

以茆诗松、程依明和濮晓龙编著的《概率论和数理统计》教材为例，结合应用统计学专业人才培养方案和本科生的知识结构，在第五章统计量及其分布中，频数分布表、直方图和茎叶图在应用统计学专业先前课程《统计学》中会涉及到，这些内容可以不讲，让学生在课后用统计软件SPSS或者R操作实现。删去多个次序统计量及其函数的分布，该内容对大部分学生来说太难，继续深造的学生可以在硕士阶段学习这部分内容。一些较难的定理证明可以省略。充分统计量这一节内容学生难以理解，可以省略不讲，尽管后继内容有涉及，不学充分统计量不会影响到后继内容的学习。在第六章参数估计中，EM算法，贝叶斯估计可以省略不讲，了解最大似然估计的渐近正态性，最小方差无偏估计中的充分性原则、Cramer-Rao不等式这些内容，对于较难理解的一致最小方差无偏估计的求解，教师也可以不用讲解。非参数检验内容在应用统计学专业后继课程《非参数统计》中会出现，教师可以省略不讲。一元线性回归可以略讲，这部分内容也出现在应用统计学专业先前课程《统计学》课程中，教师可以讲解一元线性回归的统计软件SPSS或者R操作过程和结果解释。

三、教学方法的探讨与研究

（一）类比归纳法

所谓类比，就是由两个对象的某些相同或相似的性质，推断它们在其他性质上也有可能相同或相似的一种推理形式。所谓归纳，是指从许多个别的事物中概括出一般性概念、原则或结论的思维方法。

教师可以通过对相似概念或相关内容进行类比与归纳，分析它们的相同点及不同点，找出它们的共性和个性，加深对概念、方法的理解，弄清楚各部分之间的区别和联系，培养学生的逻辑思维能力。

例如：在讲解经验分布函数定义的时候，联系分布函数的定义和性质进行对比，加深对经验分布函数定义的理解，很自然地引出格里纹科定理;在统计量及其分布这一节，可以将样本均值、样本方差、样本标准差、样本矩、样本偏度、样本峰度、样本分位数和样本中位数这些概念与概率论中的随机变量的数学期望、方差、标准差、k阶矩、偏度系数、峰度系数、分位数和中位数进行比较，让学生们思考它们之间是否有联系，自然而然地引出后续章节中的矩法估计，而且根据类比，由随机变量的变异系数的定义可以引申出样本变异系数的定义（在本教材中还未涉及样本变异系数的相关知识）;在讲解单个次序统计量的分布时，可以将最大次序统计量与最小次序统计量的密度函数对比n个随机变量的最大值和最小值的密度函数;在讲解最大似然估计的不变性时，可以对比一下矩估计的不变性，但无偏估计不具有不变性，最大似然估计通常是渐近正态的，可以与矩估计一般都具有相合性对比，进而阐明点估计的几个评价标准;在讲解假设检验的教学内容时，可以将假设检验与置信区间对比，例如，“正态均值？滋的1-？琢置信区间”与“关于？拽0：？滋=？滋0 vs ？滋≠？滋0”的双侧检验问题的显著性水平为？琢的检验是一一对应的;在推导单因素方差分析的拒绝域的形式时，可以对比分布的拟合检验的拒绝域形式的推导，将单因素方差分析与两样本的t检验相比较。

又例如：讲解置信区间这一节内容时，可以归纳单个正态总体参数的置信区间、大样本置信区间和两个正态总体下的置信区间的求法和公式，可以和枢轴量法这一般方法相对照;我们可以由单个正态总体均值的检验归纳出求拒绝域的一般方法，单个正态总体方差的检验、两个正态总体均值差的检验、两个正态总体方差比的检验和其他分布参数的假设检验都采用相同的方法求拒绝域。对于求检验的p值也是类似的。

（二）在教学中采用案例教学法

美国学者克里斯托弗·哥伦布·郎代尔首先创立了案例教学法的概念，案例教学法又称“苏格拉底式”教学法，是一种融合启发式、互动式和探究式的教学方法，教师要根据所讲授的知识点内容，提前精心准备实际生活中的典型案例，采用实际生活中的问题启发和引导学生的思维，激发学生的学习兴趣，有效培养学生分析问题和解决问题的能力。

例如：某公司要采购一批产品，每件产品不是合格品就是不合格品，但该批产品总有一个不合格品率p，若从该批产品中随机抽取一件，用X表示这一批产品的不合格数，引导学生思考如下问题：1.p的大小如何？  2.p大概落在什么范围内？3.能否认为p满足设定要求（如p小于或者等于0.05）？通过该案例，可顺利引出关于统计学这门学科的简要介绍以及相关的知识体系。

又如：在讲解最大似然估计时，可以采用如下案例：设在罐中放有许多白球和黑球，已知两种球的数目之比为1：3， 但不知哪种颜色的球多， 若采用有放回方式从罐中取3个球，发现有一只黑球，问在此情况下应估计哪种颜色的球多？如果有这个案例作为引导，学生理解最大似然估计的原理和方法就容易多了。在讲解样本量的确定时，可以介绍如下案例：某传媒公司欲调查电视台某综艺节目收视率p，为使得p的95%的置信区间长度不超过0.02，问应至少调查多少用户？通过这个案例，学生对置信区间的概念和公式理解的更加深刻。在讲解假设检验的时候，可以用女士品茶试验来引入假设检验的基本思想。我们也可以用下面一个案例引出假设检验中的一些基本概念和操作步骤：某厂生产的合金强度服从正态分布N（？兹，16），其中？兹的设计值为不低于110（Pa），为保证质量，该厂每天都要对生产情况做例行检查，以判断生产是否正常进行。某天从生产的产品中随机抽取25块合金，测得其强度值为x1，…，x25，均值为■=108.2（Pa），问当天的生产是否正常？

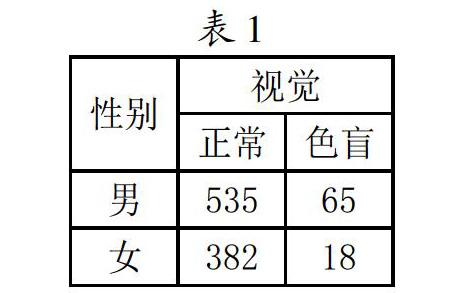
又如：在列联表的独立性检验中，可以考察如下案例：随机抽取1000人按性别（男或女）及色觉（正常或色盲）分类，得到如下二维列联表：

问：色盲与性别有无关联？

这个案例能调动和激发学生学习的积极性和兴趣，帮助他们更容易掌握列联表的独立性检验的有关概念和原理。

（三）在教学过程中渗透统计史，提高学生的科学素养和人文素养

教师在教学过程中根据教学内容融入相关知识点的统计史，重新展示统计学家关于某一问题的探索和发现以及解决的过程，不仅丰富了课堂教学内容、激发了学生的学习兴趣，还有利于开阔学生的科学视野，帮助他们更好的领会统计思想，进一步提升科学素养和人文素养。

如：在讲解t分布的教学内容时，可介绍t分布的发现过程。t分布与标准正态分布的微小差別是由英国统计学家哥塞特发现的。1908年哥塞特在Biometrics杂志上以笔名“学生”发表了使他名垂统计史册的论文，提出t分布，打破了正态分布一统天下的局面，开创了小样本统计推断的新纪元。

又如：在讲解矩估计的时候，可以介绍英国统计学家K·皮尔逊的个人生平和科学工作;在最大似然估计这一节，可以介绍德国数学家高斯和英国统计学家费希尔在最大似然估计的理论形成过程中所做的工作;在讲解一般情况下的近似置信区间时，可以介绍历史上著名的贝伦斯-费希尔问题;在讲解假设检验时，可以介绍假设检验的历史和它在数据分析中的作用，假设检验是由K·皮尔逊于20世纪初提出来的，费希尔在此基础上作了进一步的探索和研究，最终由奈曼和E·皮尔逊提出了完整的假设检验思想。

四、教学手段的探讨与研究

（一）运用板书和多媒体，二者有机结合，提高课堂教学效果

《数理统计》课程中部分公式较复杂，涉及到很多统计量;有些例题数据较多，需要用表格表示，并且计算复杂;还有些概念、定理内容，例题的题目不适合板书;等等，诸如此类都需要用到多媒体。多媒体展示，可以在很大程度上拓展课堂信息量，提高课堂教学效率。对于概念和定理的理解，定理的证明，公式的运用，例题的分析等则适合板书教学。板书教学可以给学生一定的思考时间，方便学生做笔记，有助于学生对知识的理解和掌握。在课堂上，教师有计划的运用板书和多媒体，能够最大限度地利用课堂45分钟的时间，提高课堂效果。教师在运用多媒体教学时，可以穿插使用统计软件R的展示，如在采用案例教学法时可以充分发挥统计软件R的作用。

例如：在三大抽样分布中讲解F分布时，对于F分布的定义的理解，F分布密度函数的推导，F分布的分位数的性质的推导，F分布中关于样本方差比的分布的证明，可采用板书的形式，而F分布的定义，F分布的密度函数的表达式，密度函数的图形，F分布的分位數的性质可采用多媒体展示，而对于F分布的分位数的具体例子可采用统计软件R 进行演示计算。

（二）发挥统计软件在教学过程中的作用，提高学生的数据分析能力

在教学过程中适当运用统计软件对某些不易计算或者较复杂的计算进行处理，以简化手工计算。例如，可以用统计软件R计算样本方差、样本标准差、样本矩、样本偏度和样本峰度，计算置信区间和检验的p值。

在课堂教学过程中，可以用统计软件绘制图形进行演示，例如用R软件绘制图形展示t分布和标准正态分布的密度函数形状，展示它们的微小差异。用R软件绘制正态概率图，判断某总体分布是否为正态分布。

对某些结论则用统计软件R进行模拟演示，将抽象的理论具体化后，学生更容易理解。例如：在讲解样本均值的分布的定理的时候，可以举一个具体例子用统计软件R绘制出根据1000个样本均值x的值得到的直方图，根据直方图的形状猜想出x的抽样分布为正态分布，引出样本均值的分布的定理，然后以总体为指数分布、均匀分布为例，通过一个具体例子用R软件模拟样本均值的分布，将模拟结果与定理的结论对照，加深学生对定理的理解和运用。又如我们可以用R软件模拟置信区间的频率解释。

我们也可以用R软件分析关于正态总体和非正态总体的假设检验的实际问题，根据实际问题的数据建立一元非线性回归模型;用SPSS统计软件处理分布的x2拟合检验、列联表的独立性检验、单因素方差分析和一元线性回归。我们可以在人才培养方案中适当设置《数理统计》课程的实验学时，增加学生动手实践的机会，或者在《数理统计》课程的课时不足时，教师在课堂中演示实验过程，学生课后分析实际问题，动手操作。以上这些方式方法都能较好的提高学生的数据处理、数据分析能力、建模能力和解决实际问题的能力。

我们也可以利用MOOC为学生提供丰富的《数理统计》课程学习资源，建立QQ群和微信群为学生和教师提供在线交流平台，提高学生的学习效果，也便于教师随时掌握学生的学习状态，调整教学进度，提高教学效果。

五、改变《数理统计》课程的考核方式，采用多元化的评价方式

课程考核是教学过程中的一个重要环节，教师在进行《数理统计》课程授课时，可根据自己的教学和学生的实际情况，改变传统的考核方式，在考核中，可以增加实验部分的考核。例如，采用闭卷考试，60%为期末成绩，20%为平时成绩，20%为实验操作成绩，实验操作成绩用来考核在教学过程中教师给学生布置的实践实验操作题。灵活多样的考核方式，不仅可以考查学生对理论知识的理解和掌握情况，减少学生记忆复杂公式和进行繁琐计算的负担，还可以培养学生的实际应用能力。

六、结束语

《数理统计》课程是应用统计学专业的重要专业基础必修课程，为了培养应用型人才，教师在《数理统计》课程教学中应不断进行探索和思考，并归纳和总结。本文分析了应用统计学专业《数理统计》课程的教学现状，从优化教学内容、探讨教学方法和教学手段，改变考核方式这四个方面进行探讨和研究，希望能给应用统计学专业《数理统计》课程的教学提供有价值的参考，提高大数据时代应用型人才的培养质量。

参考文献：

[1]茆诗松，程依明，濮晓龙.概率论与数理统计（第三版）[M].北京：高等教育出版社，2019.

[2]薛毅，陈立萍.统计建模与R统计软件[M].北京：清华大学出版社，2007.

[3]韦新星.应用型人才培养模式下《数理统计》课程的教学改革研究[J].当代教育实践与教学研究，2018（9）：207-209.

[4]陈聪，陈超英，纪志荣，等.统计学专业《数理统计》课程教学探索[J].教育教学论坛，2019（12）：148-149.

[5]牛成英.统计软件在《数理统计学》中的应用[J].学术纵横，2012（2）：115-116.