基于属性质量度的变精度邻域粗糙集属性约简
李 冬,蒋 瑜,鲍杨婉莹
(成都信息工程大学软件工程学院,四川成都610000)
Pawlak[1]提出的经典粗糙集是一种有效地处理模糊和不确定知识的工具.由于在处理知识系统不需要数据的附加信息或先验知识,粗糙集在某些领域的应用都取得了不错的效果[2-5].然而,经典粗糙集对于数值型的数据不能直接处理,需要事先进行离散化,但是离散化后的属性值由于没有完整的保留决策表属性值的差异,导致数据信息的缺失[6],这就限制了粗糙集的应用范围.
针对这个问题,Zadeh[7]提出了知识粒化和粒度计算的概念,Lin[8]在知识粒化、粒度计算的基础上提出了邻域模型.此后,Hu等[9]将邻域引入粗糙集,提出了基于邻域粒化和粗糙逼近的邻域粗糙集,将其应用到数值型数据的属性约简,并且提出一种快速属性约简,加快计算正域的速度.自邻域粗糙集被提出以来,众多学者也对其相关的改进与应用进行了研究[10-14].
但是,邻域粗糙集的下近似,只允许样本严格包含,这种苛刻的划分条件使得邻域粗糙集对噪声容忍能力差,对于误分类的情况过于敏感.此后,Hu等将Ziarko提出的变精度[15]引入邻域粗糙集,提出了一种变精度邻域粗糙集[9].
然而,本文发现文献[9]中变精度邻域粗糙集,其精度的变化会影响正域的划分和属性重要度的可信度,如果以属性重要度作为度量标准来选择属性,可能会将分类能力较差的属性先归入约简集合.针对这个问题,本文定义了属性质量度,以正域作为度量基础,邻域内的平均正确分类率作为正域的质量因子,并提出一种基于正域的增量和平均正确分类率的增率相结合的度量函数,通过实验分析比较,验证了算法的有效性.
1 邻域粗糙集
1.1 邻域的粒化给定决策信息系统IS=〈U,A,V,f〉,其中:U 是非空有限的对象集合{x1,x2,…,xn};A是非空的有限属性集合,A=C∪D,C∩D=∅,C是条件属性集,D是决策属性集;V是值域,表示在属性集合下的所有可能取值;f:U×A→V是一个映射函数,表示对象与其属性取值的映射关系.
定义1[9](δ-邻域) 给定决策信息系统IS=〈U,A,V,f〉,对于∀x∈U,邻域 δ(x)定义为

其中,Δ是距离函数,且对于∀x1,x2,x3∈U,Δ应满足以下条件:
1)Δ(x1,x2)≥0,当且仅当 x1=x2时等号成立;
2)Δ(x1,x2)=Δ(x2,x1);
3)Δ(x1,x3)≤Δ(x1,x2)+Δ(x2,x3).
对于N维的特征空间,距离函数通常用P范数表示
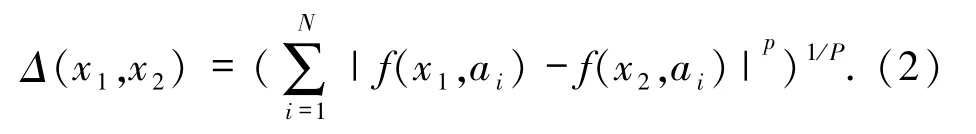
1.2 邻域决策系统
定义2[9](邻域决策系统) 给定非空的有限集合 U={x1,x2,…,xn},C 是描述 U 的实数型特征集合,D是决策属性.如果C是生成U上的一族邻域关系,则称NDT=〈U,C,D〉为一个邻域决策系统.
定义3[9]给定邻域决策系统 NDT=〈U,C,D〉,D 将 U 划分为 n 个等价类{X1,X2,…,Xn},对于∀B⊆C,决策属性D关于属性子集B的上下近似定义为:
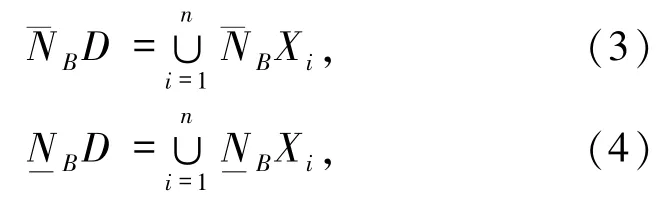
其中
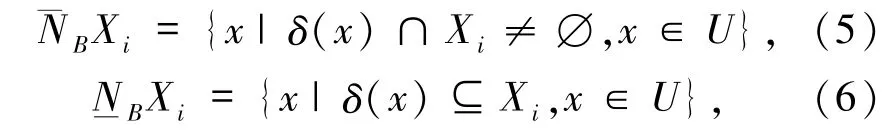
则邻域粗糙集的正域、边界域和负域依次定义为:
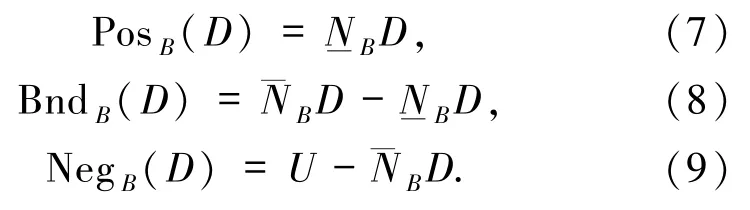
定义4[9]给定邻域决策系统 NDT=〈U,C,D〉,对于∀B⊆C,决策属性D对属性子集B的依赖度定义为

定义5[9]给定邻域决策系统 NDT=〈U,C,D〉,若有∀B⊆C,∀a∈C,但 a∉B,a相对于属性子集B关于决策属性D的属性重要度定义为
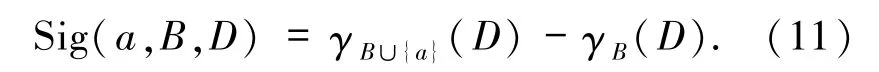
结合定义4分析可知,属性重要度取决于依赖度的变化,而依赖度取决于属性子集所划分的正域,则属性重要度可定义为

由定义4和(11)式可得
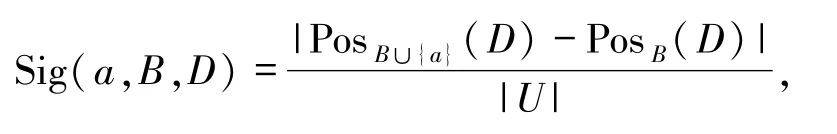
且|U|表示样本对象总数,所以属性重要度可定义为(12)式,即表示为正域的增量.
如果 Sig(a,B,D)>0,说明当添加属性 a,生成新的属性子集B∪{a}所划分正域的覆盖范围增大,各类的重叠区域减小,就可以依靠这个新的属性子集,更加准确地进行分类.
2 变精度邻域粗糙集
2.1 变精度邻域粗糙集的上下近似
定义6[16]给定邻域决策系统 NDT=〈U,C,D〉,D 将 U 划分为 n 个等价类{X1,X2,…,Xn},对于∀B⊆C,引入变精度的正确率阈值β(0.5≤β≤1),定义可变精度β-上近似和下近似为:
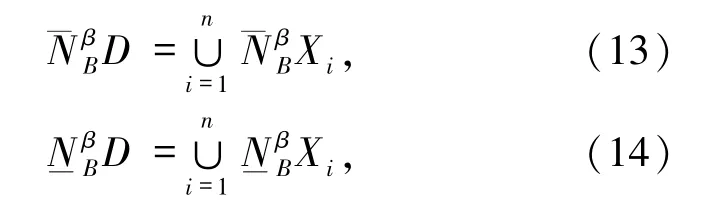
其中

由定义6易知,变精度邻域粗糙集的上下近似是基于β的容错划分,允许一定的错误分类,β的大小决定了上下近似的样本覆盖度.
2.2 变精度邻域粗糙集的属性约简改进
2.2.1 基于属性重要度的度量方式分析 以往属性约简的研究中,大多数是以属性重要度作为启发因子的前向搜索算法[9-11,16-18],其中,基于变精度邻域粗糙集的属性约简也是采用这种思想[9,16],但是由于变精度的引入,基于属性重要度的属性约简存在一定的弊端.
由定义6可知,变精度邻域粗糙集以改变阈值β来调整正域的划分,最终影响约简结果:变精度阈值β(0.5≤β≤1)越小,正域的划分条件越放松,正域的覆盖度也越大,属性约简个数越少;变精度阈值β越大,正域的划分条件越严格,正域的覆盖度也越小,属性约简个数越多.对于不同数据集,要取得最优的约简,往往变精度阈值β取值是不确定的,在实验过程中需要不停调整阈值β,找到最适合的值,但在此后属性重要度的计算中,却忽略了阈值β对正域的影响,所以需要对(11)式属性重要度进行改进.
总的来说,在文献[9]的变精度邻域粗糙集中,对属性重要度的计算忽略了β对正域的影响,使得属性重要度的可信度降低,可能导致分类能力差的属性先划入约简集合.所以,如何在引入变精度提高容错能力,同时又能避免变精度对正域的影响是本文要解决的问题.
2.2.2 一种基于属性质量度的度量函数 本文在Hu等所提出的属性重要度[9]基础上进行改进,将邻域内平均正确分类率的增率作为属性重要度的质量因子,定义了属性质量度,并提出一种基于正域的增量和平均正确分类率的增率相结合的属性选择方法,优先选择分类能力更好的属性.
定义7给定邻域决策系统NDT=〈U,C,D〉,若有∀B⊆C,∀x∈PosB(D),X∈U/D,且 x∈X,则正域内样本邻域的正确分类率定义为
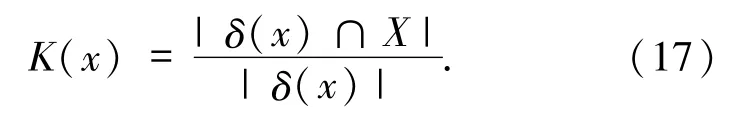
K(x)度量了正域中任一样本的邻域正确分类率,表示为邻域中所包含样本是同类别的比例,且β≤K(x)≤1.
定义8给定邻域决策系统NDT=〈U,C,D〉,若有∀B⊆C,∀a∈C,但 a∉B,且
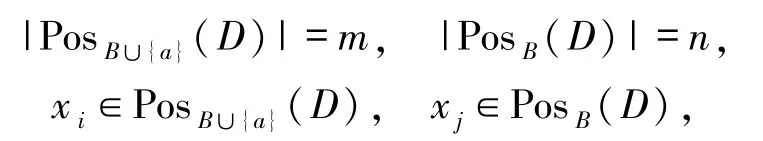
则a相对于属性子集B的平均正确分类率的增率定义为

1)当 Inc(a,B,D)<0,所添加属性 a使得正域的质量度下降;
2)当 Inc(a,B,D)=0,使得平均增益持平,正域质量不变;
3)当Inc(a,B,D)>0,所添加属性 a提高了正域的质量度,是最理想的结果.
那么Inc(a,B,D)可以作为正域的质量因子,监督正域的变化情况.
定义9(属性质量度) 给定邻域决策系统NDT=〈U,C,D〉,若有∀B⊆C,∀a∈C,但 a∉B,则a相对于属性子集B的属性质量度定义为
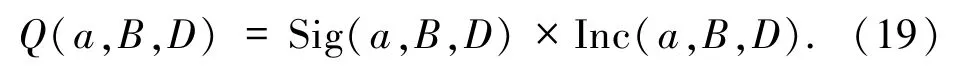
Q(a,B,D)是属性本身、属性相对的属性子集以及决策变量三者构成的一个函数.在同等情况下,属性质量度的大小可以作为属性选择的评价指标.
本文提出的度量函数有以下几点改进:
1)引入正域内样本领域的正确分类率作为正域的质量因子;
2)定义属性质量度,将正域的增量和平均正确分类率的增率相结合.
定义10[9]给定邻域决策系统 NDT=〈U,C,D〉,称B⊆C是C的一个约简,B需满足:
1)∀a⊆B,γB-{a}< γB;
2)γB(D)=γC(D).
条件1)要求在一个约简中不存在多余的属性,所有的属性都应该是必不可少的;
条件2)要求约简不能降低系统的区分能力,约简应该与全部条件属性具有相同的分辨能力.
2.2.3 计算示例邻域决策信息系统的论域
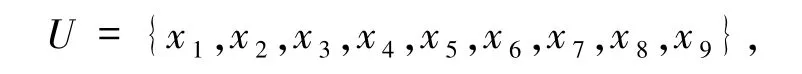
条件属性集合 C={a,b,c},决策属性集合 D={d},d将样本划分为 small、medium、large等 3 个类别,简记为 S、M、L,见表1.
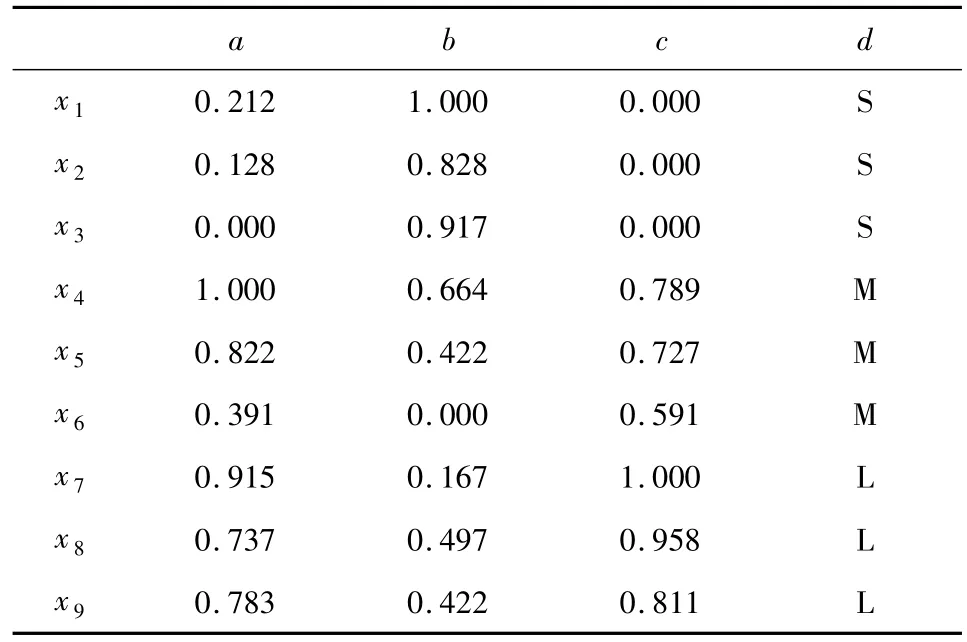
表1 归一化的决策表Tab.1 Normalized decision table
由于数据集的每个条件属性具有不同的分布特征,本文采用属性的标准差作为邻域,为每个属性设定基于自身分布特征的邻域.这里选用属性标准差的1/2作为邻域,如表2所示.

表2 邻域半径的取值Tab.2 The neighborhood radiuses
距离度量采用曼哈顿距离(P=1)计算所有属性子集的邻域,本文做如此简写{x1,2,3,4},如表 3所示.
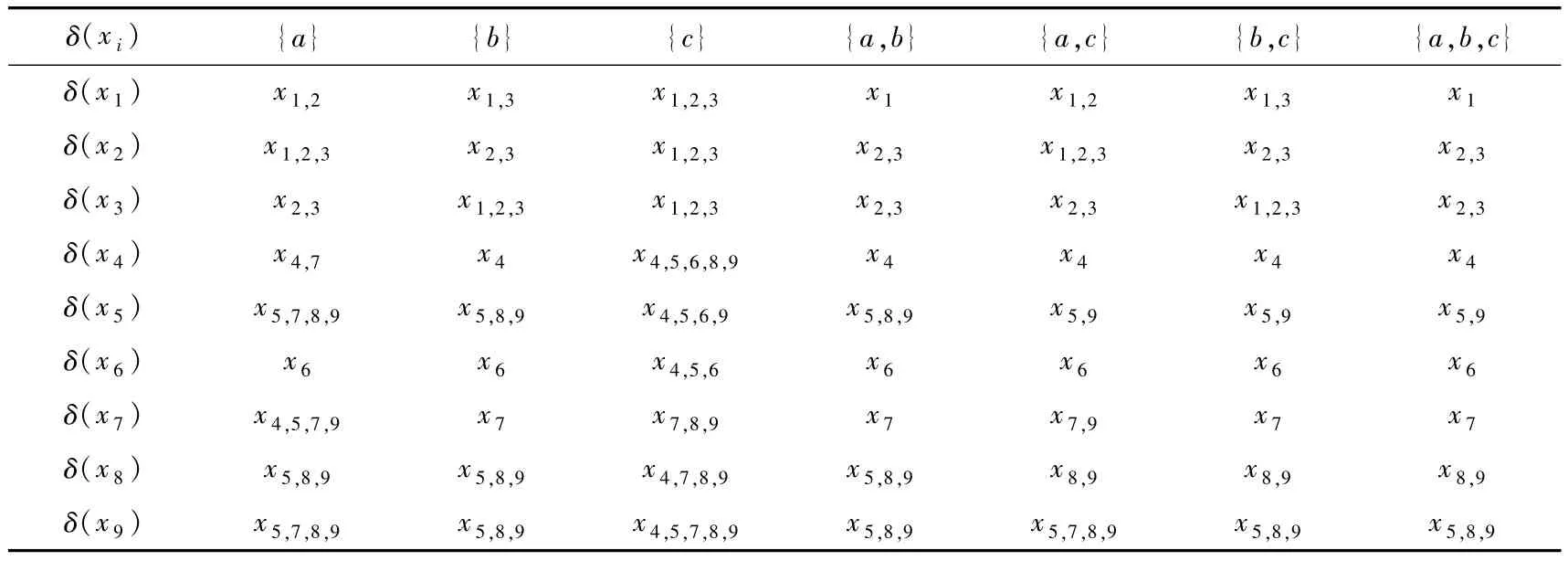
表3 所有属性组合的邻域Tab.3 Neighborhoods of all attribute combinations
根据表1,决策属性将论域划分为3个等价类:X1={x1,x2,x3},X2={x4,x5,x6},X3={x7,x8,x9},设定正确率阈值β=0.7,约简集合red=∅.
对于表3,根据(4)式和定义9可以求得:
1)属性{a}、{b}、{c}的下近似和属性质量度分别为:
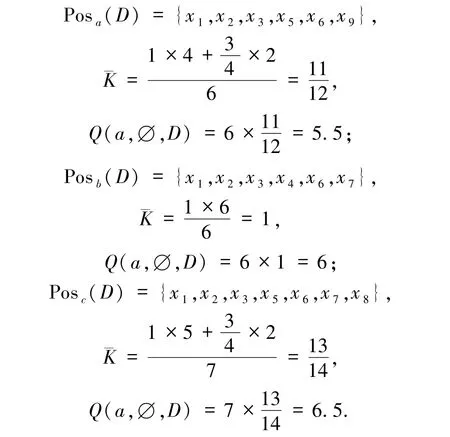
因此,选取最大属性质量度的属性为c,red={c}.
2)在选取属性 c的基础上,属性子集{a,c}、{b,c}的下近似和属性质量度分别为:
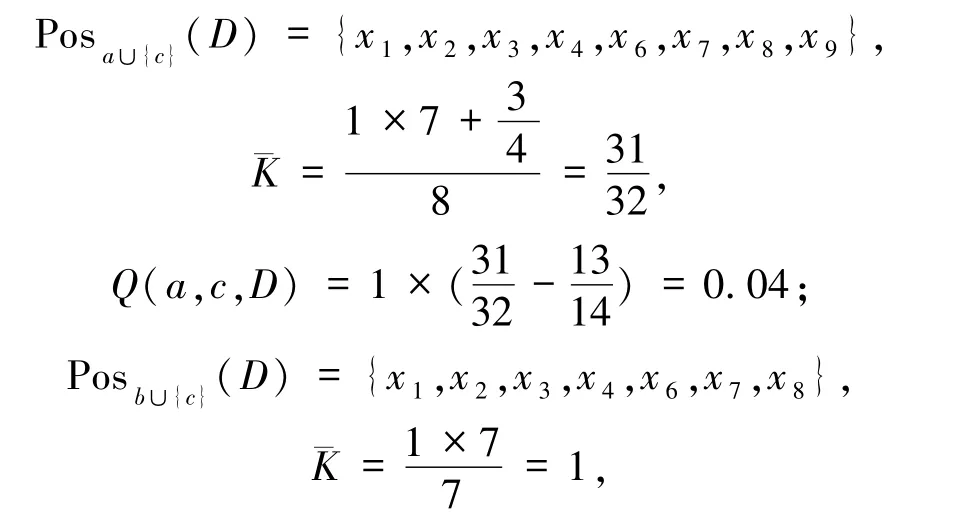
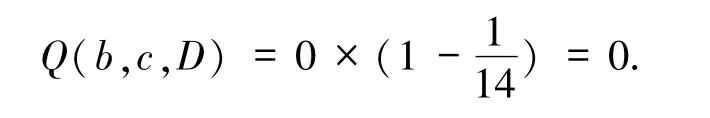
因此,选取最大属性质量度的属性为a,red={c,a}.
3)对全集 C:Posc(D)={x1,x2,x3,x4,x6,x7,x8,x9},则有 Posc(D)=Pos{a}∪{c}(D),约简集合red={c,a}.
3 基于属性质量度的属性约简算法
3.1 算法依赖于新提出的属性选择度量函数,构造变精度邻域粗糙集前向搜索属性约简算法,具体算法步骤如下:
输入:归一化后的邻域决策信息系统NDT=〈U,C,D〉,变精度阈值 β,正域的增量下限 Sig_ctrl,平均正确率的增率下限Inc_ctrl.
输出:属性约简集合red.
第一步:∀ai∈C,通过定义1对样本划分邻域.
第二步:初始化red=∅.
第三步:∀ai∈C-red:
(Ⅰ)通过定义8,计算平均正确分类率的增率Inc(ai,B,D);
如果 Inc(ai,B,D)=0,
Inc(ai,B,D)=Inc_ctrl;
(Ⅱ)通过(12)式,计算ai相对于red的属性重要度(正域的增量)Sig(ai,red,D);
(Ⅲ)通过定义9,计算ai相对于red的属性质量度 Q(ai,B,D).
第四步:找出属性质量度 Q(ai,B,D)最大的属性ai.
第五步:如果 Sig(ai,red,D)≥|U|×Sig_ctrl:
red=red∪{ai},
转到第三步;
否则,输出red.
Step 6:算法结束.
上述算法中,Sig_ctrl是为了确保选出的属性能有效提高当前属性子集对知识的表达能力;Inc_ctrl是为了避免当平均正确分类率持平,而出现属性质量度 Q(ai,B,D)=0 的情况.
3.2 算法时间复杂度分析该算法的计算主要集中在第一步对所有样本的邻域计算和第三步~第五步每次迭代求取最优的属性子集所需的正域计算次数.
假设邻域决策系统NDT=〈U,C,D〉,其中有n个条件属性,约简后有k个属性.在第一步中需要计算每个样本在不同属性下的邻域集,其度量计算次数为|U|2n次,所以时间复杂度为 O(|U|2n).在第三步~第五步中,通过每次循环找出最优的属性子集,直到得出约简结果,其正域的判定次数为
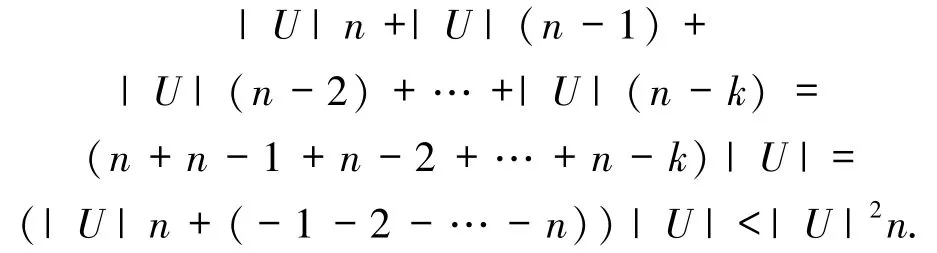
所以该步骤的时间复杂度为O(|U|2n).因此,该算法的时间复杂度最终为O(|U|2n).
4 实验分析
4.1 实验环境与方案为了验证本文算法的有效性,在UCI数据集中选取如表4所示的8个数值型的数据集,其中Diabetic Retinopathy Debrecen简写为DRD.所有实验都在PC机上运行,配置为:Inter(R)Core(TM)i5-7300HQ CPU @ 2.5 GHz,8 GB内存,Windows10操作系统,Python实验平台.
本文算法和文献[9]中Hu提出的NFARNRS算法做对比,主要是比较不同变精度阈值下的属性约简、分类精度以及样本错分数.为了比较不同算法所选属性的分类能力,本文选择当前广泛使用的C4.5和SVM分类学习算法,以10折交叉验证的平均分类精度来衡量所选择属性的分类能力.

表4 数据集Tab.4 Data sets
在邻域的取值中,都采用属性标准差(Std/2.6)作为邻域半径,距离度量采用曼哈顿距离,并且设定正域的增量下限Sig_ctrl=0.01,平均正确率的增率下限Inc_ctrl=0.01.在本文的实验中,变精度阈值β取值为0.6~0.9,以0.1为步长,在每个阈值下进行实验比较.
4.2 实验结果对比
4.2.1 属性约简结果对比 表5和表6记录了在不同阈值下本文算法和NFARNRS算法的属性约简集合.分析可知,对于不同的阈值β,2种算法得到的属性约简个数是基本一致,但是所选属性存在差异,这说明本文算法在不增加约简个数的基础上,改变了属性选择的优先度(表中属性按照选择顺序从左到右排列),这符合2.2.1的分析.而且,在个别阈值下本文的属性约简个数更少,这说明本文算法在精度变化时的属性约简效果要更优.
4.2.2 不同分类算法下的分类精度对比 表7记录了原始数据集在C4.5和SVM下的分类精度.
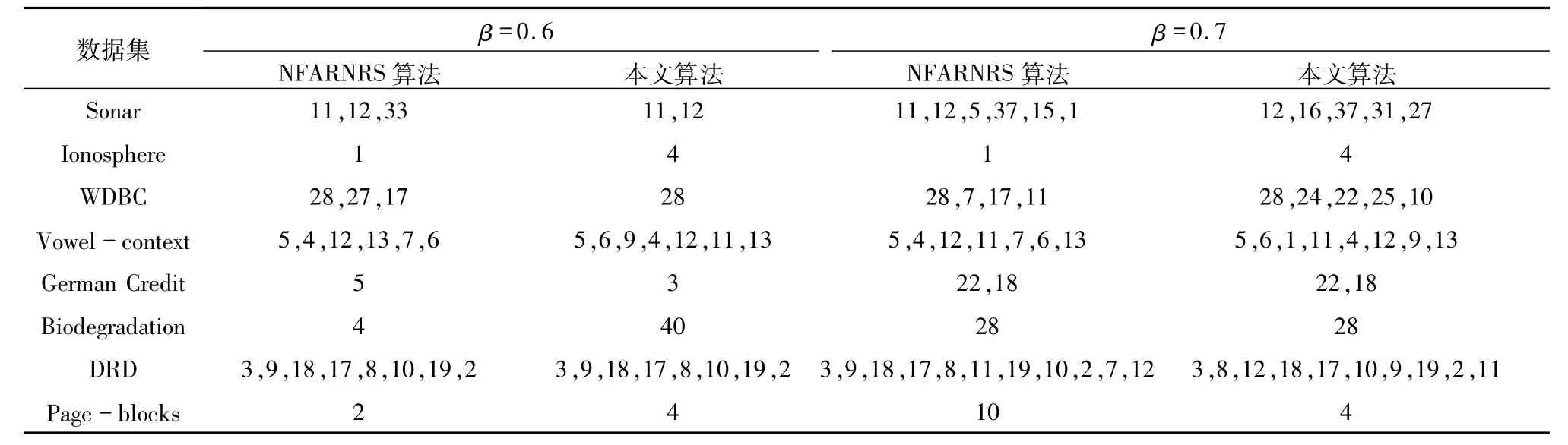
表5 不同阈值(β=0.6,0.7)下的约简对比Tab.5 Reduction comparison under different thresholds(β =0.6,0.7)
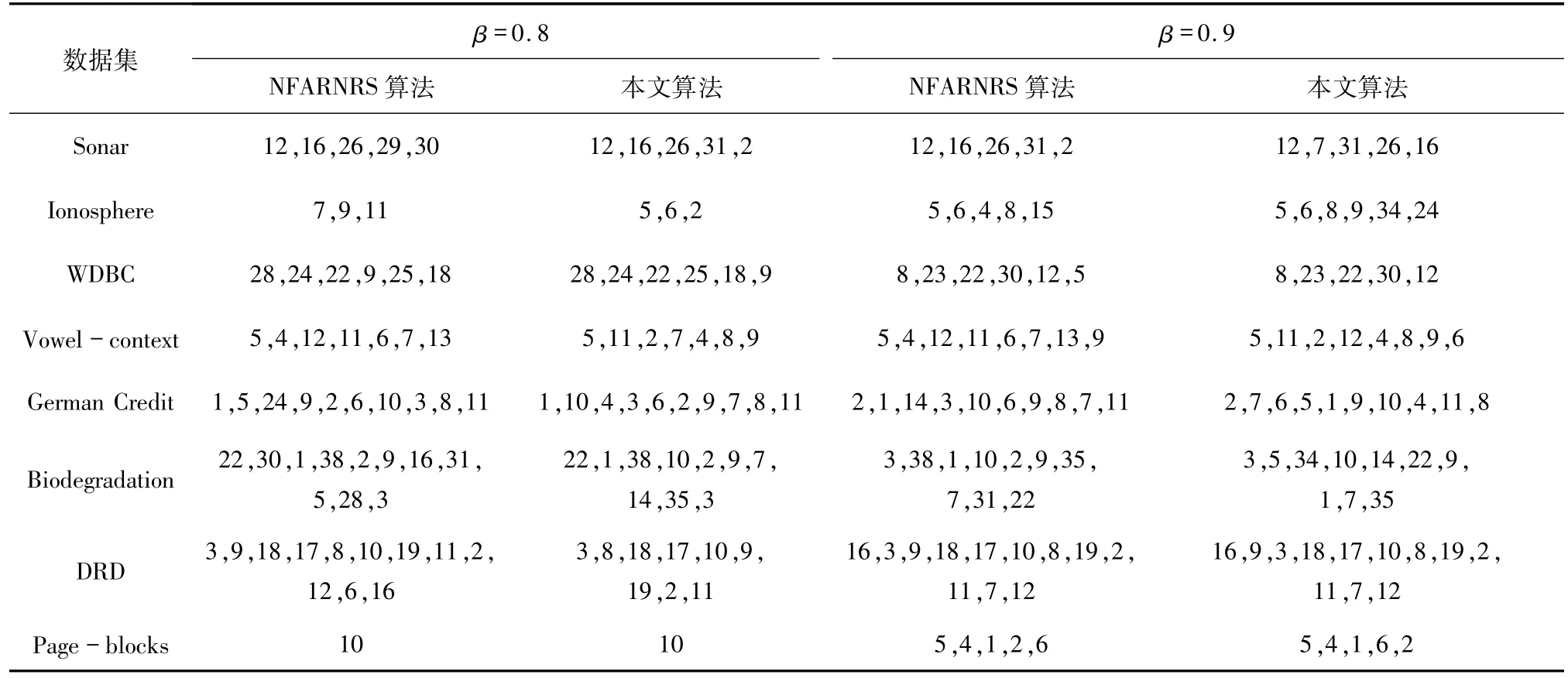
表6 不同阈值下(β=0.8,0.9)的约简对比Tab.6 Reduction comparison under different thresholds(β =0.8,0.9)
表8~11是在不同阈值和分类器下,2种算法对数据集约简后的分类精度和样本错分数的对比(样本错分数能直观的体现分类精度的差异).分析可知,当阈值β在区间变化时,本文算法所取得的分类精度在不同的分类器下总体上都更优(√:本文算法高于NFARNRS算法;--:二者持平.),且本文算法取得的最优分类精度同表7原始数据集的分类精度对比可知,在不同的分类器下,本文算法的约简都能够保持或者有效提高分类精度,这表明本文算法在2.2.2小节所提出的属性度量函数是正确有效的.图1和图2为所有数据集在C4.5和SVM的平均分类精度曲线.

表7 原始数据集的分类精度Tab.7 Classification accuracy of original data sets
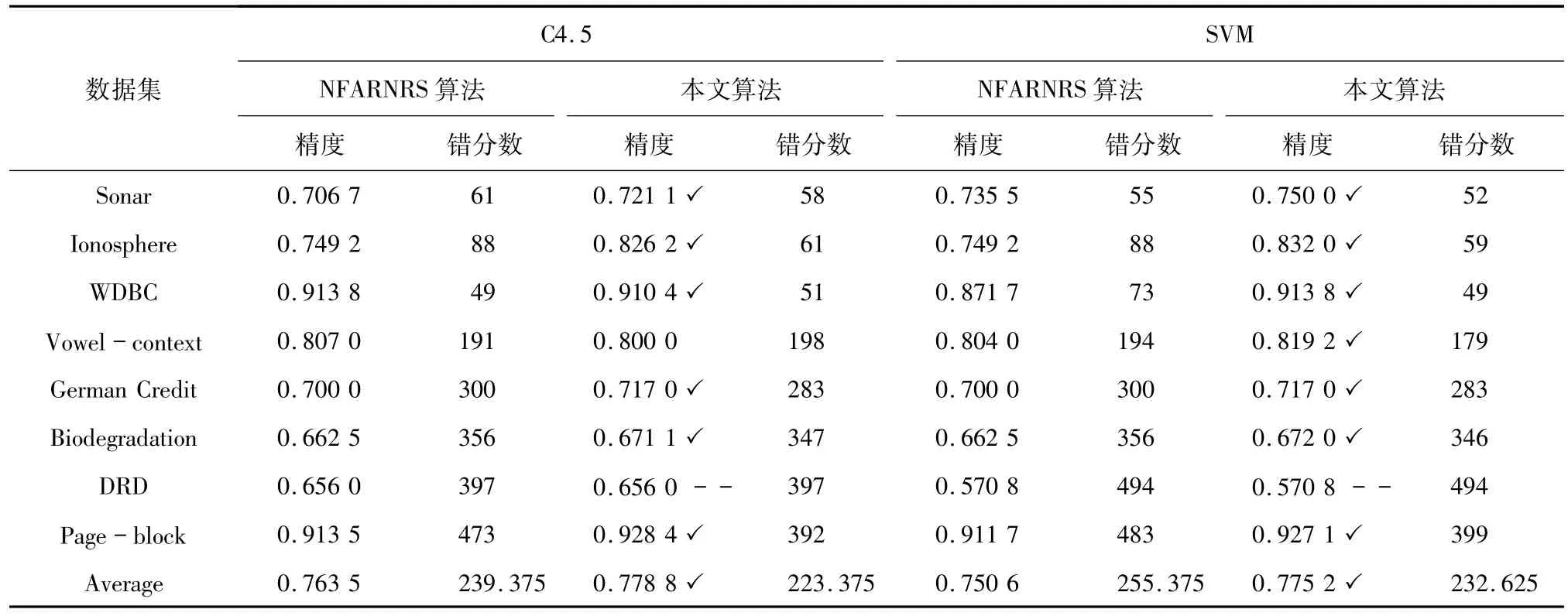
表8 变精度β=0.6的分类精度Tab.8 Classification accuracy with variable precision β=0.6
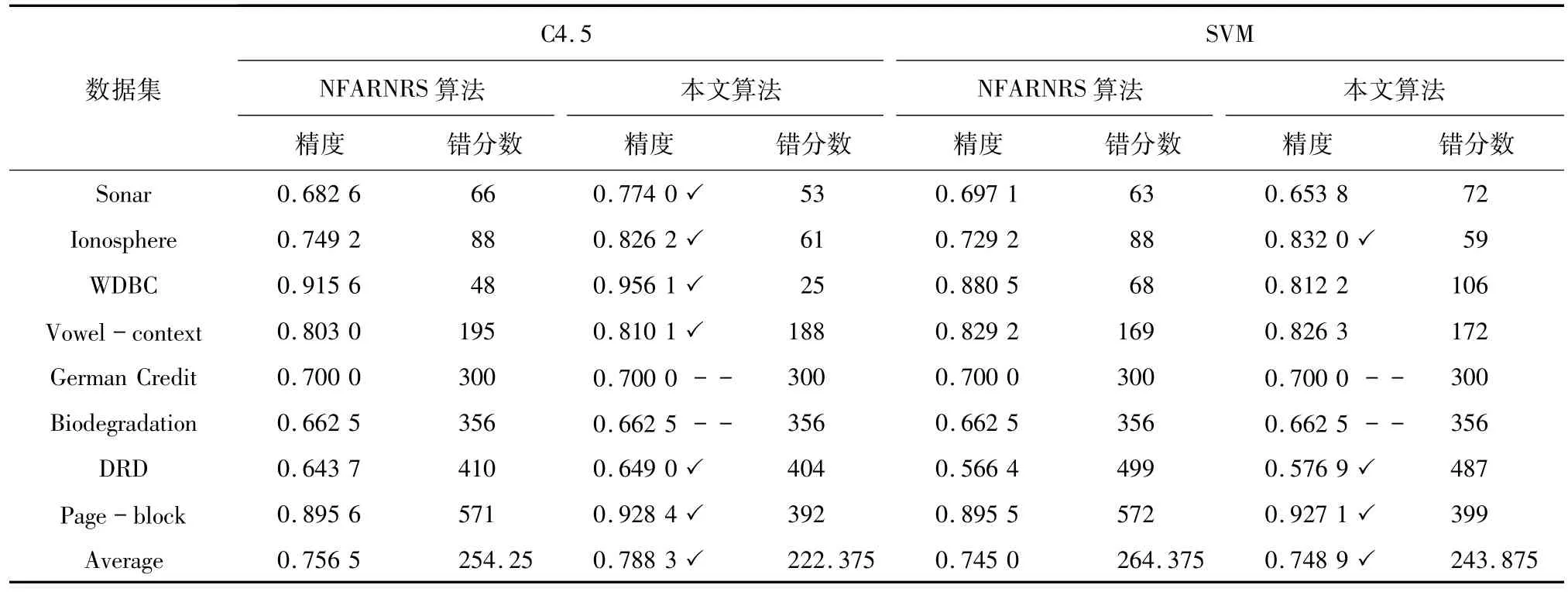
表9 变精度β=0.7的分类精度Tab.9 Classification accuracy with variable precision β=0.7
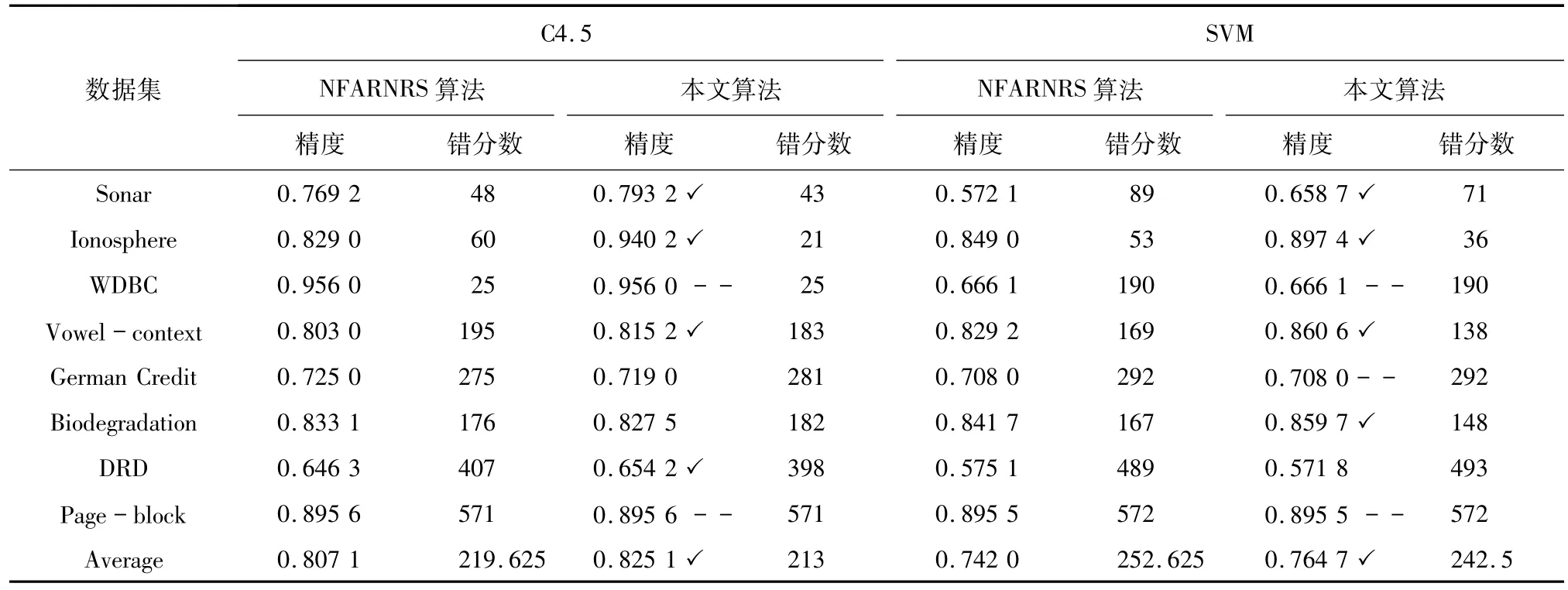
表10 变精度β=0.8的分类精度Tab.10 Classification accuracy with variable precision β=0.8

表11 变精度β=0.9的分类精度Tab.11 Classification accuracy with variable precision β=0.9
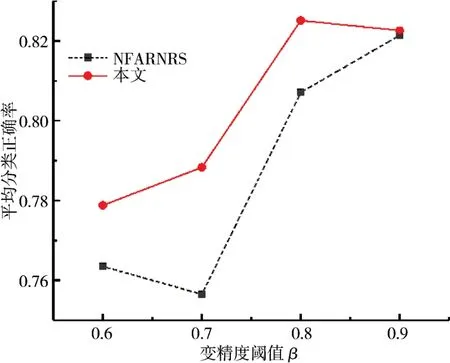
图1 所有数据集在C4.5的平均分类精度Fig.1 Average classification accuracy of all data sets in C4.5

图2 所有数据集在SVM的平均分类精度Fig.2 Average classification accuracy of all data sets in SVM
分析图1和图2的曲线可知,从总体的平均数据来看,测试数据集在本文算法下所得的平均分类精度在NFARNRS算法的曲线之上,表明基于本文算法的属性约简效果更优.而且,当β<0.9,本文算法的提升效果十分显著;而在β≥0.9时,由于分类率的平均增益变化减小,此时属性质量度主要由正域主导,本文算法和NFARNRS算法的差异就会逐渐变小,所以二者结果将会达到一致.但是本文算法对β的适应性更强,能在不同阈值下都得到更优的属性约简,表明本文提出的属性度量方式更适用于变精度邻域粗糙集的属性约简.
4.3 阈值参数的取值分析不失一般性,分类精度会随 β的增大而增大,且在本研究中,当 β∈{0.8,0.9}时,所取得的分类精度最好.但是,不同数据集的差异性,使得β的取值是无法普遍在此范围取值,由表8~11就可看出,个别数据集在β∈{0.6,0.7}就能取得不错的分类精度,这也是图1和图2中曲线跳跃的原因.
且由表5和表6可知,阈值β的改变使得约简个数呈线性变化,随阈值β取值的增大而增多.
综上,一般来说,调高β的取值可得到好的分类精度,但约简个数会稍多一点;调低β的取值可以取得更少的约简个数,但分类精度会略低.
4.4 实验结论由以上实验分析对比可知,本文算法相比于NFARNRS算法,在保持所选属性个数基本一致,甚至更少的情况下,本文算法提出的属性度量函数在不同阈值和不同分类器下基本都能得到最优的分类精度.而且,本文算法降低了阈值β对正域的影响,提高了对属性的度量能力,使得本文提出的属性度量方式更适合于变精度邻域粗糙集.
5 结束语
本文介绍了邻域粗糙集和变精度邻域粗糙集的基本概念,分析了以往变精度邻域粗糙集采用属性重要度作为度量标准的缺点,改进了属性的度量方式.相比于NFARNRS算法,本文算法通过引入邻域内正确分类率作为正域的质量因子,降低了变精度对正域的影响,在改变阈值的情况下,都能得到更优的约简.
但与以往的属性约简相比,时间复杂度仍然没有改变,如何让本文算法具有较少的时间开销,这个问题将在未来的工作中进行研究.
致谢成都信息工程大学青年学术带头人科研基金项目(J201609)对本文给予了资助,谨致谢意.

