基于开关周期性耦合的混沌系统量化同步

陈 跃,黄振坤,宾红华,陈 娟

(集美大学理学院，福建 厦门 361021)

0 引言

基于文献[1]的工作,混沌系统的同步被广泛应用到各个领域,如生态系统、信息处理、信息安全等领域[2-4]。混沌系统控制是一个具有挑战性的课题,近几年来学者们对其提出了很多富有成效的控制方法,比如最优控制[5]、自适应控制[6]、有限时间控制[7]、滑模控制[8]等。

目前大多数研究都是考虑两个相同或者相似连续耦合混沌系统的同步现象[9]。基于Lyapunov稳定性理论,文献[10]提出了一种新的滑模方案来控制受到不确定因素和外部干扰的非线性混沌系统。在实际应用中,系统之间的耦合连接有时会断开[11],系统之间的耦合可能是间歇性的,这在一定程度上可以描述为间歇性耦合。因此将研究范围由连续耦合的混沌系统扩展到不连续耦合的混沌系统是有必要的。对控制系统的量化研究一直受到人们的重视,并产生了很多有意义的成果[12]。一些学者发现量化作用对混沌控制系统的影响要比对传统的控制系统的影响大得多。然而到目前为止,这方面的研究还没有引起足够的重视。

从最近的研究来看,Lyapunov稳定性理论是讨论两个不连续耦合的混沌系统最常用的工具[13]。根据这个理论给一些充分条件可以实现两个耦合混沌系统的同步。但是那些条件对于不连续耦合的混沌系统却是无效的。文献[14]研究了两个不连续耦合混沌系统的同步问题,具有量化效应的两个不连续耦合混沌系统的同步课题值得进一步探索。基于常微分的稳定性理论和比较定理,本文建立一些新的充分条件,揭示具有量化效应控制器与系统同步及平均时间耦合强度的依赖性,表明在耦合强度较小的情况下也能实现系统的完全同步。

1 预备知识

设混沌系统为

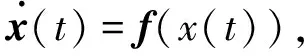
(1)

其中：x(t)=(x1(t),…,xn(t))T是系统的状态向量；f：Rn→Rn是连续可微的非线性向量函数。

要实现系统的同步,含开关周期性静态对数量化控制器的响应系统为:

(2)

其中y(t)=(y1(t),…,yn(t))T是响应系统的状态向量。

控制器u(t)设计为:

u(t)=q(v(t)),

(3)

v(t)=-k(t)e(t)。

(4)

其中：e(t)=y(t)-x(t)是驱动混沌系统与响应系统之间的同步误差；u(t)=(u1(t),…,un(t))T。量化函数[15]q(·)：Rn→D是分段常值向量函数,D是Rn中的有限子集,即把Rn划分成有限个形如{z∈Rn：q(z)=i,i∈D}的量化区域,这里采用静态对数量化器:

(5)

其中：η=(1-ρ)/(1+ρ),wi构成q量化水平集S={±wi,wi=ρiw0,i=0,±1,…}∪{±w0}∪{0},0<ρ<1,w0>0。

在文献[15]中,定义ηq=lim sup(#g[])/(-ln)为量化器q(·)的量化密度，其中#g[]为上式中的量化级数在区间[,1/]内的数量。量化密度ηq随着区间[,1/]的增长呈对数形式增长。当量化级数有限时,从ηq的定义可以得到ηq=0。当ηq比较小时,量化级数也比较少,此时量化器也比较“粗糙”。因此在下面的讨论中,称ρ为量化器q(·)的量化密度。

对此类量化器,显然有q(v)=(I+Δ)v,其中I∈Rn×n,量化同步误差Δi∈[-η,η](i=1,2,…,n)且

(6)

选取一个开关周期性的耦合强度k(t)[16]：

(7)

其中：n=0,1,2,…；k是正常数；T是开关周期；θ(0<θ<1)是开关率。显然,当0<θ<1时,式(3)是不连续耦合；当θ=1时,式(3)是连续耦合的。

下面给出混沌系统同步所用到的假设。

假设1对于函数f(x),存在一个正常数l，使得

|f(x)-f(y)|≤l|x-y|,∀x,y∈Rn。

(8)

注1 条件(8)通常被称为全局Lipschitz条件,l是Lipschitz常数。容易知道一些著名的混沌系统都能满足假设1,例如Chua’s circuit[17]、Rossler-like system[18]、Genesio system[19]等。

定义1 对于混沌系统(1)和(2)的初始值x(0),y(0),如果下面的条件成立，

(9)

则这两个系统能够实现完全同步。

引理1(比较定理)[20]设E是R2上开集,g∈C[E,R],假设以下初值问题的解存在,且解的最大存在区间为[t0,t0+h]，

dx/dt=g(t,x),x(t0)=x0。

(10)

设u(t)∈C[(t0,t0+h),R],t∈[t0,t0+h)时,有(t,u(t))∈E,u(t0)≤x0,且

Du(t)≤g(t,u(t)),t∈[t0,t0+h)。

(11)

其中Du(t)为固定的Dini导数,则

u(t)≤x(t),t∈[t0,t0+h)。

(12)

2 主要结果

定理1 系统(1)和(2)在控制器(3)的作用下能够实现同步,如果假设1成立且设计控制器耦合强度k(·)和量化信号误差范围Δ满足

(13)

证明对误差系统求导

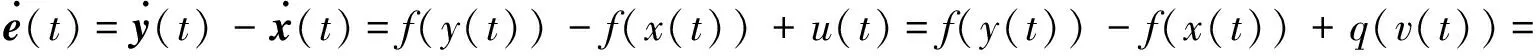
f(y(t))-f(x(t))-(I+Δ)k(t)e(t)。

(14)

满足假设1的情况下,对于任意的初值e(0)=y(0)-x(0),方程(14)有唯一全局渐进稳定解e(t,e(0))，e(t,0)≡0是系统(14)的常数解。如果这个初始解是全局渐进稳定的,那么对于每一个初始值,系统(1)和(2)能够实现完全同步.

构造Lyapunov函数V(t)=eT(t)e(t)/2。两边求导,结合式(14)和假设1得

eT(t)l|y(t)-x(t)|-eT(t)(I+Δ)k(t)e(t)=leT(t)|e(t)|-eT(t)(I+Δ)k(t)e(t)≤

l|eT(t)e(t)|-λmin(I+Δ)k(t)|eT(t)e(t)|=-2[λmin(I+Δ)k(t)-l]V(t),

(15)

由于k(t)是间歇性的,按区间[nT,(n+θ)T)和[(n+θ)T,(n+1)T)依次分段应用引理1,有

V(t)≤Γ(t),

(16)

其中n=0,1,2,…,Γ(t)是

dΓ(t)/dt=-2[λmin(I+Δ)k(t)-l]Γ(t)

(17)

由式(17)得

(18)

显然,t在[0,∞)上存在正整数m,使得t∈[mT,(m+1)T)。设t=mT+t1(0≤t1

(19)

根据k(t)的定义,得

(20)

由式(20),有

Γ(0)exp{-2mT[(λmin(I+Δ)k-l)θ-l(1-θ)]+2lt1}=

Γ(0)exp[-2mT(λmin(I+Δ)kθ-l)+2lt1],

(21)

注意到mT=t-t1,那么

Γ(t)≤Γ(0)exp[-2(t-t1)(λmin(I+Δ)kθ-l)+2lt1]=

Γ(0)exp[-2t(λmin(I+Δ)kθ-l)]exp(2λmin(I+Δ)kθt1)，

(22)

故

(23)

(24)

3 仿真实例

考虑Rössler-like系统作为例子,它是一个三维的常微分方程组:

(25)

它的响应系统是:

(26)

由式(6)和方程(14)知

即u1(t)=-(1+Δ1)k(t)e1(t),u2(t)=-(1+Δ2)k(t)e2(t),u3(t)=-(1+Δ3)k(t)e3(t),

(27)

当α=0.03,β=1.5,γ=0.2,μ=1.5,λ=0.75,ξ=21.43, ϑ=0.075时,Rössler-like系统(25)有混沌吸引子,如图1。

显然,当l=0.492 6时,Rössler-like系统满足Lipschiz条件。

4 结论

本文利用Lyapunov稳定性理论和比较定理,分析了基于量化控制的开关周期性耦合混沌系统的同步动力学,给出了不含时滞下混沌系统同步化准则,揭示具有量化效应控制器与系统同步、平均时间耦合强度的依赖性,表明在耦合强度较小的情况下也能实现系统的完全同步,本文的结果是对现有文献[14]结果的拓展,仿真例子验证了结果的可行性。