基于KdV方程的浅水畸形波演化特征

高森林，扈 喆，张晓莹，马亚州，毛富丰

(集美大学轮机工程学院，福建 厦门 361021)

0 引言

畸形波是一种能量高度集中的灾难性波浪，具有大波高、大波陡、无预兆、持续时间短等特征，其巨大的破坏力，给船舶的航行安全和海洋结构物的安全运作带来严重威胁。为了获得畸形波海上实测数据，许多研究机构投入了大量人力物力。Sand等[1]报道了1969—1984年在丹麦和爱尔兰沿海大陆架上观测到的9个浅水畸形波，这9个畸形波均发生在水深20～40 m处，有义波高2～8 m。Nikolkina等[2]更加详细地报道了2006—2010年发生在全球各处的30个浅水畸形波，这30个浅水畸形波发生在水深0～50 m处，有义波高1.0～6.0 m。

由于畸形波的海上实测存在诸多困难，人们主要依赖实验模拟和数值模拟来研究畸形波。与实验模拟相比，数值模拟可模拟更为复杂、尺度更大的波浪，且具有经济性高、误差小等优点[3]。Kriebel等[4]提出了由随机波列(或背景波列)加上瞬态波列(或脉冲波列)的双波列叠加模型，并将组成波的频谱能量按不同比重分别分配给随机波列和瞬态波列。裴玉国[5]基于双波列叠加模型改进得到三波列叠加模型(一个随机波列和两个瞬态波列)，模拟非线性更强的波浪时效果优于双波列叠加模型。Pelinovsky等[6]在KdV方程框架下，先以目标畸形波为初始条件，发展得到各个时刻的色散小振幅波，然后改以得到的色散小振幅波为初始条件，根据KdV方程关于变换x→-x,t→-t的不变性，逆转时间过程发展得到目标畸形波。为便于称呼，以下简称这一方法为时空反演法。Fouque等[7]运用时间反演法，研究了Boussinesq框架、KdV框架、粘性Burgers框架下畸形波的弱色散性和弱非线性。Akhmediev等[8]借鉴时空反演法，研究了在非线性薛定谔方程框架下两个以上Akhmediev呼吸子碰撞产生畸形波的初始条件。Touboul等[9]采用时空反演法，研究了Serre-Green-Naghdi系统下浅水畸形波底部压力分布。

目前文献中多采用有限差分法数值求解KdV方程[10-12]。与有限差分法相比，虚拟波谱法(pseudo-spectral method)在保证计算精度的同时大幅提高了计算效率[13]。Fornberg等[14]应用虚拟波谱法数值模拟了多孤子在KdV方程、mKdV方程框架下的相互作用过程。Lo等[15]应用该方法数值求解了Dysthe方程。张运秋[16]应用该方法数值求解了考虑粘性阻尼作用的四阶修正非线性薛定谔方程。本文使用虚拟波谱法数值求解KdV方程。

目前文献中多采用Longuet-Higgins提出的线性叠加模型，通过多个不同周期、不同振幅、不同随机初相位的余弦波叠加来模拟随机波浪[17-19]。但在近岸浅水区，椭圆余弦波相比余弦波更能准确地描述波浪运动特征[20]。因此本文借鉴双波列模型的思想，以JONSWAP谱为目标谱，分别基于线性余弦波与椭圆余弦波理论建立背景随机波浪场。采用时空反演法，研究高斯脉冲型畸形波在随机背景波浪场中从生成到消失的全过程，并采用小波方法分析时频演化特征。在此基础上，本文模拟多组不同参数下的高斯脉冲畸形波演化过程，回归分析高斯脉冲型畸形波持续时间和传播距离与各参数之间的关系。

1 控制方程与虚拟波谱法求解

在一维浅水中，设水深为h，并且是一个常数。假设波沿x正方向传播，波幅为a，波长为L，则当a/h≪1且h/L≪1时，水波控制方程近似演变为KdV方程[21]：

(1)

式中：t为时间；x为水平位置，η为自由液面高度。

为使用虚拟波谱法数值求解KdV方程，将方程(1)表示为如下的广义非线性方程形式：

∂η/∂t=L(η)+N(η)。

其中：L(η)、N(η)分别表示方程的线性部分和非线性部分。

虚拟波谱法的主要思想是将原非线性方程中的线性部分和非线性部分在每一个时间步长上分开求解后再进行迭代。

这样就由η(x,t)求解得到前进一个时间步长后的值η(x,t+Δt)，循环这一过程即可完成KdV方程的数值求解。

通过对比KdV方程孤波理论解与数值解来验证虚拟波谱法求解的正确性。KdV方程孤波解为[22]：

(2)

式中：c1,x0,t0为常数；c1h/3为孤波的波高；x0,t0反应了波的初始相移。

由图1可以看出数值解与理论解在各个时刻吻合良好，体现了本文数值解法的准确性与稳定性。

2 数值算例与讨论

2.1 高斯脉冲在KdV框架下的演化特征

高斯脉冲广泛应用于各类非线性问题研究中，并常作为畸形波的试探解。Pelinosky等[6]模拟了KdV框架下高斯脉冲在由18个随机正弦波叠加而成的波浪场中的发展过程。黄峻堃等[23]研究了非线性薛定谔方程框架下含有三阶、五阶非线性项和Kerr色散项时高斯型脉冲中各参量随传播距离的演化规律。与其他畸形波形式相比，高斯脉冲具有参量数目少，参量的几何意义明显等优点，便于使用控制变量法等方法进一步量化分析。

本文采用时空反演法模拟KdV框架下高斯脉冲从生成到消失的全过程。以高斯脉冲

η(x,0)=Ae-x2/d2

(3)

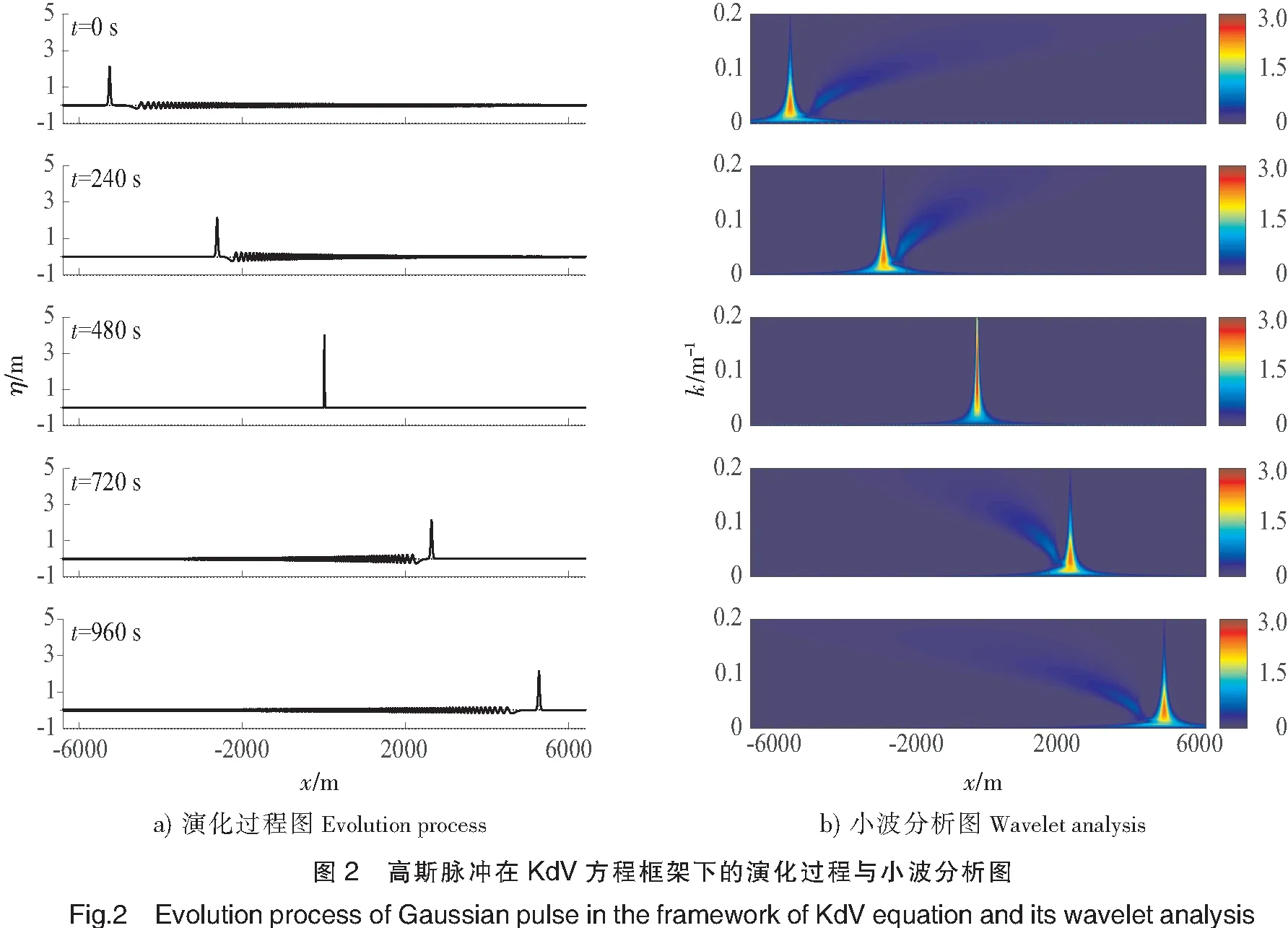
为目标波，取波幅A=4 m,脉宽d=10 m，使用虚拟波谱法求解KdV方程，可得波列的发展过程，如图2所示。

图2a各个时刻的波形图体现了KdV方程框架下畸形波的时空聚焦生成机制。在t=0s时刻，波列由左端的大振幅波和右端的色散小振幅波列组成。由于大振幅波前进速度大于小振幅波列，随着时间的推移前者逐渐追赶后者，到t=480s时刻，大振幅波与小振幅波列在x=0m位置汇聚形成高斯脉冲；t=480s时刻之后，高斯脉冲分解为右端的大振幅波和左端的色散小振幅波列，且右端的大振幅波振幅逐渐减小。图2b的小波分析图反映了各个时刻波列的波数组成信息和能量分布信息。在t=0s时刻，左端大振幅波对应的是波数0～0.15 m-1呈三角形尖峰状部分，为能量主要集中区域；右端色散小振幅波列呈扇状，并与尖峰状部分波数0.03 m-1处连接对应，能量较小；到t=480s时刻，扇状部分消失，能量集中到高斯脉冲生成位置x=0m处，同时高波数部分能量明显增加；t=480s时刻之后，能量分散到呈尖峰状的右端大振幅波和呈扇状的左端小振幅波，并且随着时间推移，整个波列的波数逐渐减小。

2.2 高斯脉冲在随机线性余弦波浪场中的演化特征

采用Goda改进的JONSWAP谱[24]为目标谱，模拟随机波浪。JONSWAP谱的表达式如下：

线性波浪叠加法将海浪看作由多个不同周期和不同随机初相位的余弦波叠加而成：

本文结合实际观测数据[1,2]，计算时取水深h=10m，有义波高Hs=2m，有义周期Ts=10s。首先以ζ(x,0)为初始条件代入KdV方程，采用虚拟波谱法，计算得到在KdV框架下充分发展后波形稳定的随机波列ζ(x,600)，再取目标畸形波波列为

η(x,0)=ζ(x,600)+Ae-x2/d2。

(4)

以式(4)为初始条件求解KdV方程，采用时空反演法可得随机线性余弦波浪场中高斯脉冲型畸形波从生成到消失的过程，如图3所示。

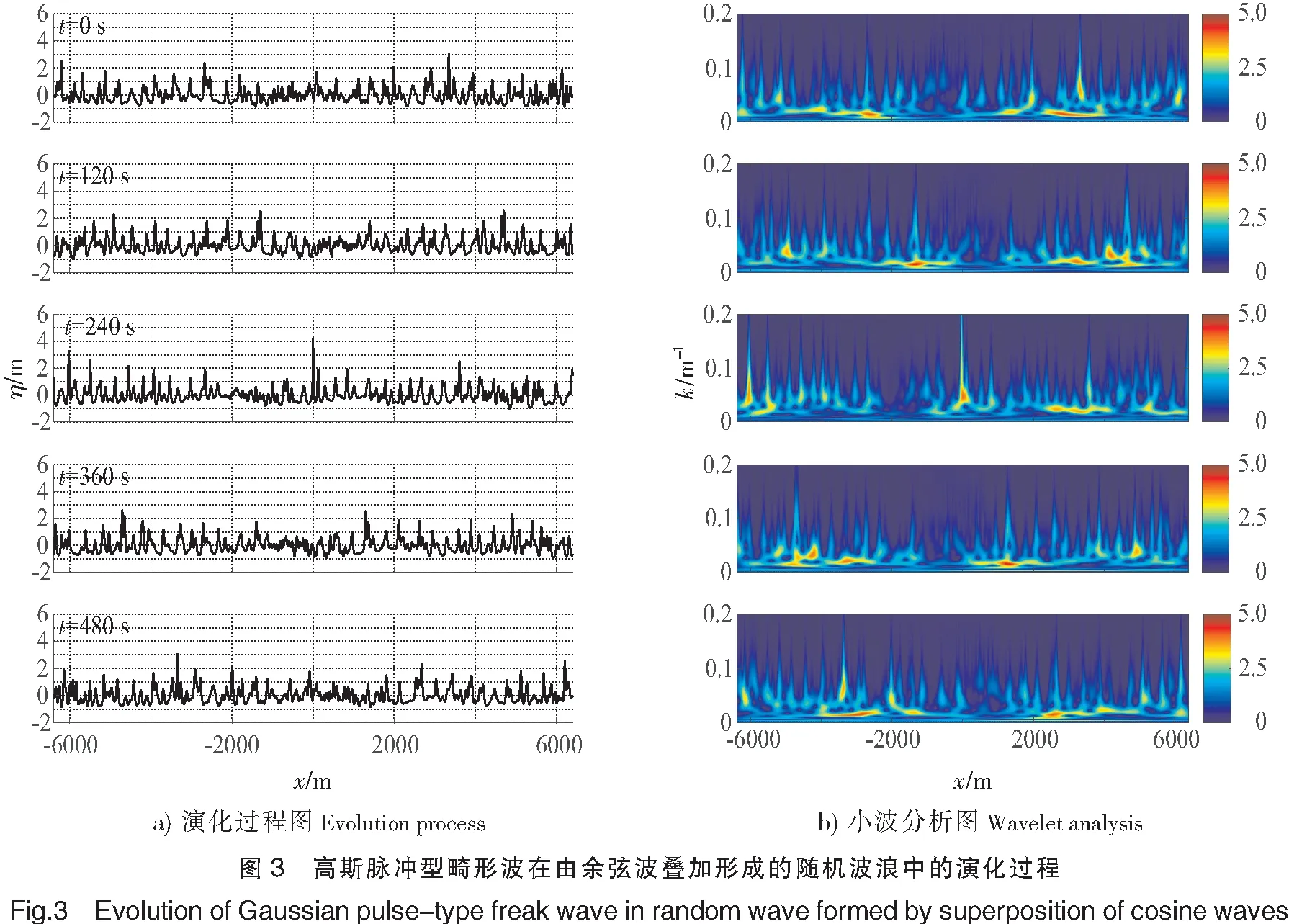
图3a各个时刻的波形图显示了高斯脉冲型畸形波在t=240s时刻生成，之后逐渐消失在随机波浪场中的过程。与波形图相对应，图3b各个时刻的小波分析图反映了高斯脉冲在随机波列中演化过程，从t=0s到t=240s，高斯脉冲波列在随机波列中汇聚，最终在x=0m处形成高斯脉冲型畸形波；从t=240s到t=480s，高斯脉冲波列在随机波列中色散，能量分散到随机波列中。纵观各个时刻小波图可以发现，在高斯脉冲型畸形波生成前的t=0s和t=120s时刻，以及生成后的t=360s和t=480s时刻，波列的高波数(波数0.1～0.2 m-1)成分能量较少且分散，而在畸形波生成t=240s时刻，波列能量会聚到畸形波生成x=0m处，且x=0m处高波数成分能量大而集中，这体现了畸形波能量集中，且能量向高频转移的特点。

2.3 高斯脉冲在随机椭圆余弦波浪场中的演化特征

波浪传入近岸浅水区后，海底边界的摩擦影响迅速增加，波高和波形将不断变化，两波峰处的水质点运动特性与波陡H/L的关系减弱，而与相对波高H/d的关系增强，即H/L和H/d成为决定波动性质的主要因素，此时采用能反映决定波动性质的主要因素H/L和H/d的椭圆余弦波理论，描述波浪运动，可以取得较满意的结果[20]。

在t=0s时刻，第i个椭圆余弦波可以表示为[25]

首先以ζ(x,0)为初始条件代入KdV方程，采用虚拟波谱法计算得到在KdV框架下充分发展后波形稳定的随机波列ζ(x,600)，再取目标畸形波波列为η(x,0)=ζ(x,600)+Ae(-x2/d2)，得到椭圆余弦随机波浪场中高斯脉冲型畸形波从生成到消失的全过程

与由余弦波模拟的随机波列类似，由椭圆余弦波模拟的随机波列中高斯脉冲型畸形波也经历了由汇聚到色散的演化过程，如图4所示。在t=240s时刻，x=0m处出现了高斯脉冲型畸形波，同时能量也会聚到x=0m处，且高波数成分能量明显增加；t=240s时刻之后，畸形波波幅减小，能量逐渐消散，高斯脉冲型畸形波“消失”在随机波列中。图4b的小波能量图分析与图3类似，再次验证了畸形波发生时的高能量与高波数能量集中特点。

2.4 高斯脉冲型畸形波持续时间与传播距离

采用控制变量法研究不同参数的高斯脉冲型畸形波在椭圆余弦随机波浪中的持续时间与传播距离规律。采用上跨零点法计算波列演化过程中各个时刻的最大波高与有义波高，当最大波高超过2倍有义波高时，按畸形波定义可知，该时刻波列中出现畸形波，进而可计算畸形波从出现到消失的持续时间与传播距离。本节继续沿用上文取定的水深h，有义波高Hs，有义周期Ts数值，选取3组随机相位，然后依次改变高斯脉冲表达式(3)中的波幅A，脉宽d，共形成66个算例，并计算每个算例中畸形波持续时间Δt和传播距离Δs，无因次化后结果如图5、图6所示。

由图5可知，当高斯脉冲脉宽d固定时，随着高斯脉冲无因次波幅A/Hs增大，高斯脉冲型畸形波在椭圆余弦随机波浪中的无因次持续时间与无因次传播距离均随之增大。由图6可知，当高斯脉冲波幅A固定时，随着高斯脉冲无因次脉宽d/Ls增大，高斯脉冲型畸形波在椭圆余弦随机波浪中的无因次持续时间与无因次传播距离也随之增大。对图5、图6中的计算结果进行最小二乘法曲线拟合，拟合函数选为二次函数，由图5、图6可见拟合效果良好。由此可以得出结论：高斯脉冲型畸形波的持续时间与传播距离与高斯脉冲波幅A和脉宽d都是正相关的，且大致呈二次函数关系。从能量角度分析，高斯脉冲波幅A与高斯脉冲能量大小正相关，而脉宽d则反映了高斯脉冲能量在波峰处的会聚程度，因此当高斯脉冲能量越大，能量越会聚到波峰处，则高斯脉冲型畸形波在椭圆余弦随机波浪中的持续时间越长，传播距离越远。

3 结论

本文采用虚拟波谱法数值求解KdV方程，得到不同初始波列下的发展波列，并通过小波变换对各个时刻波列进行分析，清楚显示了各个时刻波列能量分布变化。以JONSWAP谱为目标谱，分别以线性余弦波、椭圆余弦波为基础组成波，采用叠加思想模拟随机波列，同时根据KdV方程的性质，采用时空反演法，实现了随机波列中畸形波从出现到消失的完整演化过程。最后计算分析了不同参数条件下高斯脉冲型畸形波在椭圆余弦随机波浪中的持续时间与传播距离。

结合以上各算例分析可得如下结论：1)畸形波生成时能量集中，且高波数部分能量明显增加，体现了KdV方程的非线性；2)高斯脉冲型畸形波的持续时间与传播距离和高斯脉冲的波幅与脉冲参量之间为二次函数关系。当畸形波能量越大，畸形波处能量集中程度越高时，畸形波的持续时间越长，传播距离越远。

本文方法具有一定普适性，如文中的高斯脉冲型畸形波可替换为其他类型的畸形波，KdV方程可替换为其他适合使用时空反演法的方程，进而研究不同类型畸形波在随机波浪场中的演化特征。