基于MATLAB/Simulink的TBM边滚刀动力学模型及振动分析

张斌荣， 管会生， 谭孝锋， 廖 江， 杨 骁， 李 霞

(西南交通大学机械工程学院， 四川 成都 610031)

0 引言

盘形滚刀作为TBM掘进机的开挖部件，其破岩特性的好坏直接影响到施工质量和效率。滚刀根据其安装位置可分为中心滚刀、正面滚刀和边滚刀。边滚刀由于安装倾角较大，与刀盘上其他滚刀相比承受着较大的侧向力，磨损失效更严重。秦岭隧道施工平均每开挖248 m，边滚刀就需要更换刀圈，其平均寿命只有正面滚刀的1/5[1-2]。陈馈[3]统计了重庆过江隧道盾构刀具磨损情况,发现边滚刀的报废量大于中心滚刀。Hassanpour等[4-5]统计了伊朗Karaj输水隧道工程的换刀情况，结果显示边滚刀的磨损最为严重。

硬岩地层中，边滚刀滚压岩石产生剧烈冲击振动。工程实践表明，边滚刀较大的安装倾角使其除了承受垂向力外还承受着较大的轴向载荷与倾覆力矩，恶劣的受载条件极易引起刀圈偏移、断裂、挡圈移位、轴承过载和密封失效等一系列问题，加剧刀具的磨损，从而降低边滚刀的使用寿命。对边滚刀进行动力学和振动特性的研究有助于优化滚刀结构、降低磨损、延长寿命。

针对此问题，一些学者做出了部分成果。张旭[6]建立了包括TBM滚刀和刀座的整体多自由度动力学模型，研究受载情况下的系统振动响应。贺力克等[7]、王志富[8]建立了盘形滚刀沿垂直于刀盘面的垂向振动模型，并进行了仿真求解。霍军周等[9]建立了盘形滚刀的垂向-轴向动力学模型，并研究了滚刀部件不同的刚度、质量及外部载荷对滚刀振动的影响。李涛[10]重点关注了轴承在载荷传递上的复杂性，计算了轴承每个滚子的受载和变形状况，由此建立了滚刀多自由度耦合动力学模型，并对比分析了不同位置滚刀的振动。张魁[11]将滚刀与岩石联合起来作为研究对象，建立了滚刀在不同地层中的垂向振动模型。

目前针对边滚刀的研究较少，部分研究局限于对边滚刀垂向振动的研究或仅考虑垂向和轴向振动，鲜有考虑倾覆力矩对滚刀侧向摆动的影响。本文将TBM边滚刀破岩时所受载荷等效为垂向载荷、轴向载荷和倾覆力矩，合理简化模型，针对滚刀垂向、轴向振动和刀具侧向摆动建立7自由度动力学模型；运用MATLAB/Simulink的相关模块搭建了求解该模型的仿真框图，对动力学系统进行仿真求解；通过改变滚刀各部件的刚度值，研究刚度对滚刀不同方向振动和摆动的影响。

1 边滚刀动力学模型建立

破岩时滚刀刀圈主要受垂向力Fn、侧向力Fs和滚动力Fr作用；刀载荷均通过刀体、轴承和轴传递到刀座上。由于侧向力作用于刀圈上，相对于滚刀中心会产生转动力矩，使刀具发生侧向摆动。

盘形滚刀结构与受力状态如图1所示。可将滚刀侧向载荷Fs等效为作用在刀轴中心上的轴向力和相对于滚刀中心的倾覆力矩。由于滚动力Fr主要与滚刀滚动有关，对滚刀的振动影响较小，故本文对此不予考虑[10]。因此，可将滚刀破岩受到的载荷分为垂向力Fy(t)(即Fn)、轴向力Fx(t)和倾覆力矩M(t)。

图1 边滚刀结构与受力状态示意图

基于集中质量法和滚刀各部件的振动特性，将滚刀划分为3个节点部分： 刀圈等效为节点Z1，刀体等效为节点Z2，刀轴等效为节点Z3。考虑到滚刀轴承的圆锥滚子与内外圈载荷接触传递的复杂性和变形的非均匀性，采用刚性套圈理论[12]，将轴承的位移看作是内外圈之间的相对刚性移动。因此，将轴承外圈和刀体看作整体，将轴承内圈和刀轴看作整体，然后据此分别建立垂向、轴向和倾覆力矩作用下的动力学模型。

1.1 垂向振动模型

垂直载荷是引起滚刀垂向振动的激振源，建立垂向3自由度动力学模型，如图2(a)所示。振动微分方程组如式(1)所示。

(1)

1.2 轴向振动模型

将岩石作用在刀圈底部的侧向力等效为轴向力和倾覆力矩，其中轴向力Fx(t)可看作是引起滚刀轴向振动的激振源，建立轴向3自由度振动模型，如图2(b)所示，振动微分方程组如式(2)所示。

(2)

式(1)—(2)中:m、k、c、x、y分别为节点等效质量、刚度、阻尼、轴向位移和径向位移；下标中的1、2、3分别表示3个节点；下标中的x、y分别表示该物理量在轴向和径向的分量。

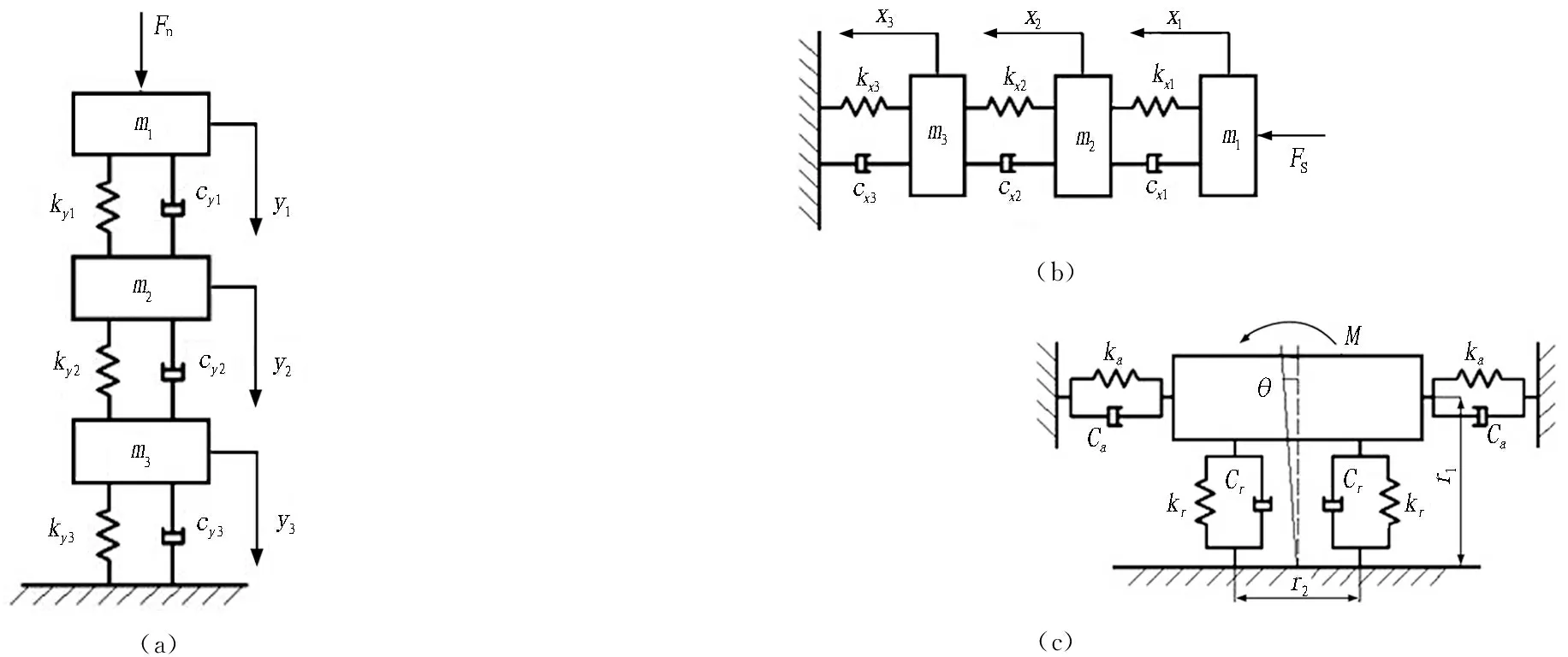
(a) (b) (c)

图2边滚刀动力学模型

Fig. 2 Dynamic model of edge disc-cutter

1.3 滚刀摆动模型

滚刀的摆动包括2方面。一是由于滚刀部件在垂向和轴向发生振动偏移而使与岩石接触的刀圈发生侧向角度摆动，如式(3)所示。

(3)

式中r为滚刀刀圈半径。

二是在倾覆力矩作用下滚刀发生侧向振动。将2个轴承的径向和轴向支撑作用简化为弹簧-阻尼模型，如图2(c)所示。弹簧-阻尼提供的反力所产生的相对于刀轴的转矩可看作是轴承为抵抗倾覆力矩而产生的反力矩。力矩作用下的摆动微分方程如式(4)所示。

(4)

式中：J、cθ分别为侧向摆动的转动惯量和阻尼；ka，kr为单个轴承轴向和径向刚度；ca、cr为单个轴承轴向和径向阻尼；r1为轴承外圈到刀轴中心的距离；r2为两轴承在刀轴上的安装距离。

因此，滚刀侧向摆动角度

θ=θ1+θ2。

(5)

1.4 动力学参数确定

1.4.1 节点等效质量

以某一实际工程施工中所使用的刀圈外边直径为432 mm的单刃盘形滚刀作为研究对象。获得滚刀三维模型各个等效质量和转动惯量数据如表1所示。

表1 各节点等效质量及转动惯量

1.4.2 节点等效刚度

Z1、Z3的等效刚度分别为滚刀刀圈与刀轴的刚度，包括径向刚度和轴向刚度;Z2的等效刚度为成对安装轴承刚度。根据罗继伟等[12]的理论，圆锥滚子轴承在轴向、径向载荷和力矩载荷的综合作用下，轴承的刚度并不是常量，而会随着轴承内外圈的相对位移和转角变化而改变。为了简化复杂的计算,同时考虑到轴承的刚度并非常量，使用式(6)—(7)分别计算单个圆锥滚子轴承径向和轴向刚度。

(6)

(7)

式(6)—(7)中：Kne为刚度系数；δr、δa分别为内外圈轴向、径向相对位移；φi为第i个滚子的位置角；Z为轴承滚子数目；αe为圆锥滚子与外滚道的接触角。

由此可计算出成对安装的圆锥滚子轴承刚度，即节点Z2等效径向和轴向刚度分别为ky2=2kr、kx2=2ka。

综上所述，可得到节点Z1与节点Z3各方向上的等效刚度，如表2所示。

表2 节点等效刚度

1.4.3 节点等效阻尼

Z1和Z3等效阻尼及摆动阻尼cθ可通过经验公式[8]计算。Z2的等效阻尼为成对安装的圆锥滚子轴承的阻尼，根据圆锥滚子轴承阻尼的计算方法[13]，可得到单个轴承的阻尼cr和ca。与圆锥滚子轴承刚度相同，单个轴承阻尼的2倍即是成对安装的圆锥滚子轴承的阻尼。由此可确定各节点等效阻尼，如表3所示。

表3 各节点等效阻尼

2 Simulink仿真

建立边滚刀关于垂向、轴向和侧向摆动的动力学模型。由式 (1)—(3)组成滚刀整体的7自由度微分方程组,滚刀动力学仿真的实质就是求解此微分方程组。MATLAB/Simulink在分析机械振动系统时，可利用元件库里合适的模块直观、迅速地建立起系统的框图模型，能够非常快速、准确地得到系统的机械振动情况，而其交互式的仿真分析方式可方便地进行模型参数的调整，分析不同参数的影响或进行参数优化。因此，本研究采用MATLAB/Simulink建立滚刀动力学的仿真框图模型,如图3所示。该系统中有3个输入模块，分别输入垂向载荷激励、轴向载荷激励和力矩载荷激励；系统分为Vertical、Axial、Rotate 3个子系统，3个子系统分别分析滚刀的垂向、轴向振动和侧向摆动，系统之间相互影响；系统的输出响应通过多个Scope模块观察；Simulink仿真采用变步长的ode45求解器。

图3 Simulink仿真框图

在MATLAB工作空间输入边滚刀的3个载荷激励，便可得到滚刀各部件不同方向上的振动曲线和摆动角度变化曲线。

3 动力学模型求解

3.1 输入载荷

运用ANSYS/LS-dyna对边滚刀破岩进行仿真，得到的滚刀破岩载荷历程可作为上述Simulink仿真框图模型的输入。设定边滚刀安装角为45°，滚刀距离刀盘中心3.14 m，滚刀绕刀盘中心旋转速度为0.24 rad/s，岩石地层确定为花岗岩地层。在仿真中定义刀圈为刚体，选取*MAT_RIGID本构模型；根据岩石材料的应力应变特点，采用基于Ottosen四参数破坏准则的动态损伤本构模型*MAT_JOHNSON_HOLMGUIST_CONCRETE[14]。刀圈与岩石材料具体参数如表4所示。

表4 刀圈与岩石材料参数

仿真得到滚刀所受到载荷变化曲线如图4所示。由图可知，滚刀载荷变化呈现先增加后略有下降最终平稳的趋势,载荷曲线锯齿形的形状也反映了岩石的“阶跃破碎”特征[15]。滚刀垂向载荷和侧向载荷变化趋势相同，由于安装角较大的缘故，滚刀侧向载荷明显较大，与垂向载荷仅相差20 kN左右。

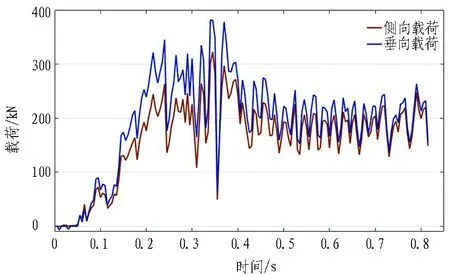
图4 滚刀载荷曲线

输入系统的垂向力即为仿真得到的垂向力，输入的轴向力即为仿真得到的侧向力，而倾覆力矩等于侧向力大小与滚刀半径的乘积。

3.2 响应分析

运用所建立的滚刀振动动力学框图模型和上述滚刀载荷进行仿真，得出边滚刀在垂向、轴向上各节点振动和侧向摆动角度变化曲线如图5—7所示。结果表明： 无论是垂向还是轴向，滚刀各部件的振动幅度波动走势与该方向上所受载荷变化趋势是一致的。由于结构中阻尼的存在，各部件振动位移响应曲线中会出现局部振幅逐渐衰减的曲线波动，但并没有影响整体响应曲线走势，所以滚刀的振动可看作是受迫振动。

图5 边滚刀各节点垂向振动曲线

图6 边滚刀各节点轴向振动曲线

图7 边滚刀侧向摆动角度变化曲线

由图5和图6可知，无论是垂向还是轴向，刀圈的振动位移最大，刀轴的最小。垂向上刀圈、轴承、刀轴最大振动位移分别为0.952、0.465、0.067 mm;轴向上最大位移分别为1.162、0.425、0.055 mm。刀圈的振动幅度远远大于轴承和刀轴，刀圈振动幅度大约是轴承的2倍，是刀轴的14倍。另外，刀圈侧向最大振动位移比垂向的大22%左右。刀圈较大的侧向位移会改变滚刀的刀间距，而刀间距是影响破岩效率的重要参数。

由图7可知，滚刀侧向摆动也十分剧烈，滚刀最大侧向摆角达到0.406°,其摆动幅度的波动趋势与载荷变化趋势基本一致。较大的摆动角度使得滚刀轴承处于偏载的状态，因此圆锥滚子轴承必须拥有合理的最大容许偏角。同时，较大的摆动角度会加剧滚动浮动密封的失效，这是边滚刀最易损坏失效的重要原因之一。

4 刚度对滚刀振动的影响

滚刀整体的振动表现为节点Z1的振动，各部件的刚度对刀具振动影响尤为重要。分别对3个节点的刚度依次增大1、2、3、4、5倍进行系统仿真，从仿真得到的响应曲线研究节点刚度因素对节点Z1影响。

保持其他节点的动力学参数不变，将前文中节点Z1的垂向和轴向刚度增大1、2、3、4、5倍，分别进行仿真分析，得到对应的刀圈振动位移曲线如图8所示。由图8可知，刀圈刚度无论增大几倍，其振动位移变化趋势相同，只是会引起曲线整体位置的变化，即平均位移的变化；且随着刚度的继续增大，振动位移的减小幅度越来越小。同样改变其他节点的刚度值进行仿真，研究这些节点刚度值变化对刀圈振动的影响。统计各垂向、轴向振动和侧向摆动曲线中的最大值，做出最大位移与刚度值变化曲线，如图9—11所示。

图8 刀圈不同刚度下的垂向位移

Fig. 8 Vertical displacement of cutter ring under different stiffness

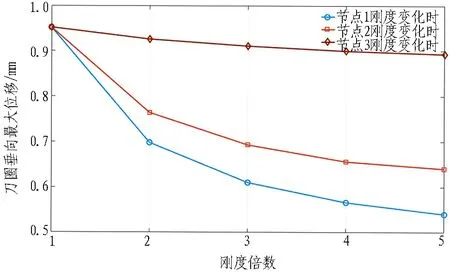
图9 刀圈垂向最大位移

图10 刀圈轴向最大位移

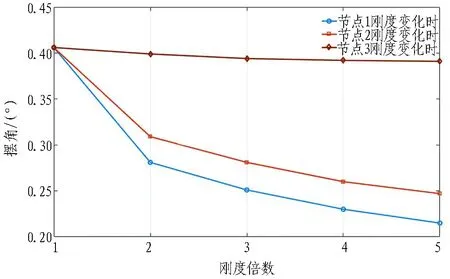
图11 滚刀摆角最大值

根据图9—11中曲线变化，计算出在不同节点刚度逐渐增大的情况下，滚刀刀圈不同方向上振动位移或角度幅值的变化率，如表5所示。

表5各节点不同刚度下刀圈振动幅值变化率

Table 5 Change rate of vibration amplitude of cutter ring under different stiffness of each node

节 点 刚度增大倍数垂向位移变化率/%侧向位移变化率/%摆动角度变化率/%Z1126.631.531.0212.716.110.737.28.18.044.65.75.5Z2119.514.121.729.46.010.535.34.97.842.62.45.2Z312.62.01.721.61.61.331.30.90.540.70.50.3

结合曲线变化与表中的数据可知： 无论是哪一节点的刚度增大，滚刀垂向、轴向振动和摆角大小均降低，且随着刚度的继续增大，位移和角度的减小幅度越来越小。而滚刀2个方向上的振动幅度和摆角大小主要受到刀圈和轴承刚度的影响。由表5可知，若将刀圈刚度增大1倍，滚刀垂向、侧向振幅和摆动振幅分别降低26.6%、31.5%、31.0%；若将轴承刚度增大1倍，滚刀垂向、侧向振幅和摆动振幅分别降低19.5%、14.1%、21.7%；而将刀轴刚度增大1倍，滚刀垂向、侧向振幅和摆动振幅分别仅降低2.6%、2.0%、1.7%。因此，无论是垂向、轴向位移还是摆动角度的大小，刀圈刚度的变化影响最大，轴承次之，刀轴几乎对振动幅度无影响。对比刀圈垂向和轴向振动位移的减小速率大小可知，对于此安装角度为45°的边滚刀来说，节点Z1刀圈的刚度增加对其轴向振动的影响比垂向振动的大；刀圈的刚度与轴承的刚度均对滚刀侧向摆动幅度有很大影响。

5 结论与建议

1)与中心滚刀和正面滚刀相比，边滚刀在掘进中承受更大的侧向载荷和倾覆力矩。对滚刀进行合理简化，建立动力学模型，输入外部载荷到该系统中可以得到刀圈、轴承和刀轴的振动位移响应，以此来研究边滚刀在破岩过程中受力振动情况。

2)针对某一安装角为45°的60 cm单刃盘形边滚刀在花岗岩岩层中的破岩过程进行分析。结果表明：滚刀各部件的振动曲线变化趋势与输入载荷基本一致；在垂向和轴向上，滚刀各部件振动幅度最大的是刀圈；边滚刀刀圈侧向振动十分剧烈，其振动幅度约大于垂向振动幅度22%，较大的侧向振动幅度会改变滚刀的刀间距，影响到滚刀破岩效率；刀具侧向振动也非常剧烈，最大摆角可达0.406°，刀圈剧烈摆动使得圆锥滚子轴承处于偏载状态，容易导致轴承边缘应力过大而发生疲劳破坏，因此滚刀设计时需合理考虑轴承最大容许偏转角。

3)通过研究滚刀各部件刚度对滚刀振动的影响发现，滚刀垂向、轴向振动和摆角大小主要受到刀圈和轴承刚度的影响。若将刀圈刚度增大1倍，滚刀垂向、侧向振幅和摆动振幅分别降低26.6%、31.5%和31.0%；若将轴承刚度增大1倍，滚刀垂向、侧向振幅和摆动振幅分别降低19.5%、14.1%和21.7%。但随着刚度的增大，振动位移降低的幅度越来越小。

此模型仍存在不足，模型中将圆锥滚子轴承简化考虑，且忽略了轴承滚道缺陷、润滑油等对轴承刚度与阻尼的影响；另外，文中只对45°安装角的边滚刀进行了分析，在下一步可深入研究不同安装角下边滚刀的振动特性。

参考文献(References)：

[1] 万治昌, 沙明元, 周雁领. 盘形滚刀的使用与研究(1): TB880E型掘进机在秦岭隧道施工中的应用[J]. 现代隧道技术, 2002, 39(5): 1.

WAN Zhichang, SHA Mingyuan, ZHOU Yanling. Study on disk cutters for hard rock: Application of TB880E TBM in Qinling Tunnel[J]. Modern Tunnelling Technology, 2002, 39(5): 1.

[2] 万治昌, 沙明元, 周雁领. 盘形滚刀的使用与研究(2): TB880E型掘进机在秦岭隧道施工中的应用[J]. 现代隧道技术, 2002, 39(6): 1.

WAN Zhichang, SHA Mingyuan, ZHOU Yanling. Study on disk cutters for hard rock: Application of TB880E TBM in Qinling Tunnel[J]. Modern Tunnelling Technology, 2002, 39(6): 1.

[3] 陈馈. 重庆过江隧道盾构刀具磨损与更换[J]. 建筑机械化, 2006, 27(1): 56.

CHEN Kui. Abrasion and replacing of cutting tools of shield machine for across Yangtse River Tunnel of Chongqing City[J]. Construction Mechanization, 2006, 27(1): 56.

[4] HASSANPOUR J, ROSTAMI J. Predicting TBM performance in second lot of Karaj Water Conveyance Tunnel (KWCT)[J]. Australian Geographer, 2009, 40(4): 387.

Although phosphor particles are small, the initial and final settling velocities are not significantly different, hence acceleration can be ignored. When the particles are stable or settling down, f can be expressed as:

[5] HASSANPOUR J, ROSTAMI J, ZHAO J, et al. TBM performance and disc cutter wear prediction based on ten years experience of TBM tunneling in Iran[J]. Geomechanics & Tunnelling, 2015, 8(3): 239.

[6] 张旭. TBM滚刀多阶段受力模型及其联接结构动态设计[D]. 大连: 大连理工大学, 2015.

ZHANG Xu. Multi-stage force model of TBM hob and dynamic design of its connection structure[D]. Dalian: Dalian University of Technology, 2015.

[7] 贺力克, 谭青, 易念恩, 等. 盾构机盘形滚刀垂向振动的建模、仿真与实验研究[J]. 机床与液压, 2013, 41(11): 49.

HE Like, TAN Qing, YI Nianen, et al. Modeling simulation and test study on the disc cutter vertical vibration in shield tunnel machine[J]. Machine Tool & Hydraulics, 2013, 41(11): 49.

[8] 王志富. 盾构机盘形滚刀垂向振动特性研究[D]. 长沙:中南大学, 2011.

WANG Zhifu. Study on vertical vibration characteristics of disc-cutter of shield[D]. Changsha: Central South University, 2011.

[9] 霍军周, 张旭, 欧阳湘宇, 等. 盘形滚刀垂向-轴向动力学模型及振动特性分析[J].机械设计与研究, 2014, 30(5): 114.

HUO Junzhou, ZHANG Xu, OUYANG Xiangyu, et al. Kinetic modeling and analysis on axial-vertical vibration characteristics for the disc cutter[J]. Mechanical Design and Research, 2014, 30(5): 114.

[10] 李涛. 强冲击载荷下TBM盘形滚刀动态特性及新结构研究[D]. 大连: 大连理工大学, 2014.

LI Tao. Research on dynamic characteristics and new structure of TBM disc hob under strong impact load[D]. Dalian: Dalian University of Technology, 2014.

[11] 张魁. 盾构机盘形滚刀作用下岩石破碎特征及滚刀振动特性研究[D]. 长沙: 中南大学, 2010.

ZHANG Kui. Rock fragmentation and hob vibration characteristics of shield under hob action[D]. Changsha: Central South University, 2010.

[12] 罗继伟， 罗天宇. 滚动轴承分析计算与应用[M]. 北京:机械工业出版社，2009.

LUO Jiwei, LUO Tianyu. Analysis, calculation and application of rolling bearings[M]. Beijing: Machinery Industry Press, 2009.

[13] 吴昊， 王建文， 安琦. 圆锥滚子轴承阻尼的计算方法[J]. 轴承， 2009(2): 5.

WU Hao, WANG Jianwen, AN Qi. Calculation method for damping of tapered roller bearing[J]. Bearing, 2009(2): 5.

[14] 朱逸. TBM多滚刀组合破岩特性的数值模拟及实验研究[D]. 长沙: 中南大学, 2013.

ZHU Yi. Numerical simulation and experimental study on rock breaking characteristics of TBM multi hob combination[D]. Changsha: Central South University, 2013.

[15] 宋克志. 泥岩砂岩交互地层越江隧道盾构掘进效能研究[D]. 北京: 北京交通大学, 2005.

SONG Kezhi. Study on shield tunneling efficiency in mudstone sandstone interactive stratum[D]. Beijing: Beijing Jiaotong University, 2005.

引用格式：冯海暴， 刘俊伟， 苏长玺. 自航式双体船拖带沉管航道尺度分析研究： 以深中通道沉管隧道为例[J]. 隧道建设(中英文)， 2020， 40(6): 840.

FENG Haibao, LIU Junwei, SU Changxi. Analysis of channel dimensions for immersed tube element towed by self-propelled catamaran: a case study on immersed tunnel of Shenzhen-Zhongshan Link[J]. Tunnel Construction, 2020, 40(6): 840.