不同刃型组合的TBM滚刀破岩数值模拟研究
侯显俊
(中铁十二局集团建筑安装工程有限公司,山西 太原 030024)
0 引 言
全断面岩石隧道掘进机(TBM)是重型专用工程装备,广泛应用于水利水电、采矿、高速公路和轨道交通领域的隧道工程。TBM的盘型滚刀主要包括常截面(CCS,Constant Cross Section)和V型截面2种。这2种滚刀的破岩效果和耐磨程度有所差别:V型滚刀的破岩效率非常高,这是因为其刃端与岩石的接触区域很小,从而可以产生很大的压缩应力,然而由于V型滚刀刃端金属材料少,随着刀刃的快速磨损和刃宽增大,其破岩效率急剧下降;与之相比,CCS型滚刀由于刃宽不随磨损发生明显变化,其破岩效率一直保持在较高水平且较为稳定。因此,最初广泛应用于TBM的V型滚刀已逐步被CCS型滚刀所取代。然而,工程实践表明,对于某些极端高硬岩地层,将部分CCS型滚刀替换成V型滚刀,可有效地提高破岩效率、降低刀盘推力,从而快速通过该区段。这种方法已在部分工程中开展应用[1],然而鲜有相应的试验、数值模拟和理论研究被报道,导致对其破岩机理理解不够深入。
全断面直线或回转破岩试验(LCM或RCM)是研究滚刀破岩机理最准确可靠的手段。基于LCM试验,科罗拉多矿业大学(CSM)提出了TBM掘进性能预测的CSM模型[2],具体包括:破岩载荷预测、掘进速度预测及滚刀寿命预测等。Tuncdemir等[3]使用14种岩石开展了大量LCM试验,研究了不同类型滚刀的影响,揭示了破岩比能与岩碴块度之间的基本关系。Balci等[4-5]使用CCS和V型滚刀开展了大量LCM试验,研究了滚刀类型和结构尺寸对破岩过程的影响规律。Xia[6]使用CCS型滚刀开展了大量LCM试验,对比了试验所得破岩载荷与CSM模型的预测载荷,发现对于高硬岩,CSM模型的预测载荷偏低。Pan[7-8]使用砂岩开展了LCM试验,研究了围压对破岩载荷和破岩效率的影响规律。Pan和Geng等[9-10]分别使用混凝土和砂岩,开展了RCM试验,研究了滚刀的安装极径和倾角对破岩载荷的影响规律。基于有限元方法的软件,如AUTODYN和ABAQUS等,已被广泛的用于研究滚刀破岩的宏观效能。Cho11-12]使用AUTODYN软件,采用其内置的Drucker-Prager本构模型定义岩石材料,研究了滚刀破岩的最佳条件及其破岩效率。Han[13]使用ABAQUS软件及其内嵌的VUMAT接口,编制了基于Mohr-Coulomb本构模型的岩石材料子程序,开展了刀盘掘进岩石的大型模拟,研究了刀盘的推力和扭矩。基于离散元方法的软件,如UDEC和PFC,已被广泛的用于研究滚刀破岩过程中的裂纹扩展等细观机理。Gong[14-15]使用UDEC软件研究了岩石节理的间距和方向对破岩效果的影响规律,模拟结果与现场结果吻合较好。Li等[16-20]使用PFC软件研究了滚刀破岩载荷及成碴机制,并开发了诸如颗粒簇等新模型,用于提高数值模拟的准确性。上述研究为揭示刀盘破岩机理做出了重大贡献。
本文采用基于有限元方法的ABAQUS软件,研究CCS和V型滚刀在不同组合模式下的破岩过程,并开展RCM试验验证所建数值模型。所建数值模型的3把滚刀的组合包括:CCS-CCS-CCS,CCS-V-CCS,V-CCS-V和V-V-V四种形式。为了研究不同刀刃磨损量和贯入度对破岩过程的影响,设定刀刃的磨损量为0、5、10、15 mm ,设定贯入度为2、4、6、8 mm。统计分析每组模拟的滚刀破岩载荷(法向力Fn和切向力Ft)、滚动系数(RC,切向与法向载荷之比)和比能(SE)。
1 数值模型及试验验证
1.1 数值模型构建
所建滚刀破岩模型如图1所示,模型由3把直径为432 mm的盘型滚刀和1块长方体岩样组成。3把滚刀以角速度ω绕各自局部坐标系的x轴自转,各滚刀的局部坐标系与滚刀中心p1、p2和p3固联,各把滚刀同时被赋予沿全局坐标系y轴的线速度v,各滚刀的线速度和角速度满足关系:v=(216-W)ω,其中W表示刀刃的磨损量,从而保证滚刀处于与实际TBM滚刀一致的“滚动”破岩状态。长方体岩样的宽、长和厚(分别对应全局坐标系x,y,z轴方向的尺寸)分别为380、200和100 mm,刀间距S为80 mm,岩样的底面和侧面施加了固定边界条件,上表面不施加边界条件。图1以3把未经磨损的CCS型滚刀作为示例,对于其他滚刀形式和磨损状态,不重复作图。

图1 滚刀破岩模型
图2(左)示意了CCS型滚刀((a)、(b)、(c)、(d))和V型((e)、(f)、(g)、(h))在不同的磨损量W下的刀刃尺寸,虚线包络区域表示已经磨损掉的金属,灰色区域表示刀刃与岩石直接接触的区域,该图以4 mm的贯入度示例,而其他贯入度下的刀刃尺寸容易同理得到,因此不重复作图;图2(右)示意了4种滚刀组合形式,定义CCS-CCS-CCS为组合1,CCS-V-CCS为组合2,V-CCS-V为组合3,V-V-V为组合4。
1.2 岩石材料定义及试验
采用一种中等强度的砂岩开展本文研究,使用胡克定律和Drucker-Prager本构模型来描述岩石的弹塑性力学行为,公式为
(1)
式中:J2为偏应力的第2坐标不变量,J2=[(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]/6;I1为主应力的第1坐标不变量,I1=σ1+σ2+σ3;A为表征静水压力影响的参数。
使用Lemaitre模型[21]表征岩石弹性模型的损伤,并控制其单元失效删除,公式为
(2)
式中:E为杨氏模量;E0为初始杨氏模量;D为损伤因子;Dc为损伤系数,与(εR-εD)同阶;εR为开始损伤起始时的塑性应变;εD为岩石破裂时的塑性应变;y为应力流动函数;Y为强度系数;μ为泊松比;σm为平均应力;σe为等效应力;Δp为等效塑性应变增量。
开展了单轴压缩试验、直接拉伸试验和直接剪切试验,用于获取砂岩的力学参数。在西安理工大学岩土实验室,参照工程岩体试验方法标准,开展了单轴压缩和直接剪切试验;在中南大学岩土实验室,参照国际岩石力学协会发布的室内和现场试验标准,开展了直接拉伸试验。所获取的砂岩力学参数如下:单轴抗压强度为78 MPa、直接拉伸强度为3.2 MPa、初始弹性模量为12.7 GPa、泊松比为0.206、内摩擦角为51.6°、黏聚力为15.8 MPa、密度为2 558 kg·m-3、摩擦因数为0.3。
由于本文着重研究岩石在滚刀作用下的破裂过程,并且由于滚刀合金材料的刚度和强度远大于岩石,模拟过程中滚刀的微量变形和磨损对模拟结果的影响忽略不计,因此把滚刀定义为离散刚体,即仅考虑其形状和尺寸。滚刀与岩石的接触采用ABAQUS中的通用接触算法。区别于传统的接触对算法,通用接触算法的相互作用主体、接触属性、接触面属性可以各自独立地指定,可以更为弹性灵活地增加模型中的接触细节。岩石单元的类型为C3D8R,即3维8节点6面体减缩积分单元。
1.3 边界条件设置
分析了不同切削速度下的比能和计算时间,如图3所示。当切削线速度vi小于20 m·s-1时,计算时间t随切削速度的增大而迅速缩短;比能SE随切削线速度的变化不大。Cho等的数值研究表明,切削速度对比能影响不大,适当提高切削速度可有效减少计算时间;Roxborough[22]的试验研究表明,滚刀破岩载荷和比能受切削速度的影响不明显。因此,选取滚刀的切削线速度为25 m·s-1左右。需要说明,虽然数值模型中的滚刀切削速度明显大于实际TBM的最大切削线速度(约2.5 m·s-1)和本文RCM试验中的切削线速度(约0.05 m·s-1),但是数值与试验结果整体接近,这是因为本构中假定岩石是应变率无关材料。
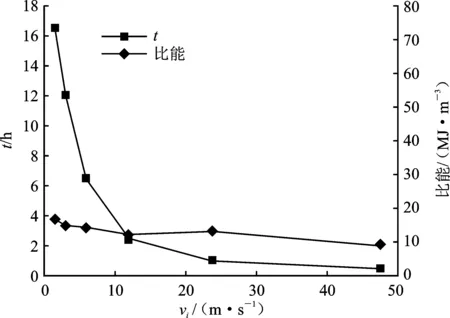
图3 不同切削速度时模型计算时间与比能
为保证模型中的滚刀与实际TBM滚刀类似的滚动破岩运动状态,本文同时设定了滚刀的切削线速度和回转角速度。建立了如图4所示的2个单刀直线切削模型,图4(a)中同时设定滚刀的线速度和角速度,称为“强制回转”,图4(b)中仅给定切削线速度,而角速度由接触产生,称为“接触回转”。2个模型的破岩效果相似,符号SDV29表示公式(2)中的损伤因子D,该因子越接近1,表示损伤越严重。但如图4(c)所示,两者载荷差距明显,“强制回转”模型的法向力Fn与试验值接近,且整体平稳,而“接触回转”模型的法向力Fn明显小于试验值,且逐渐增大;可以看到“接触回转”模型的角速度ω在切削过程中持续增大,但远小于93 rad·s-1,这是由于在给定的切削距离L内,滚刀所受到的切向力不足以克服本身的惯性,使其达到滚动状态,滚刀处于滑动为主的运动状态,与实际TBM滚刀破岩运动不符。因此,滚刀的运动状态采用了“强制回转”的设定。
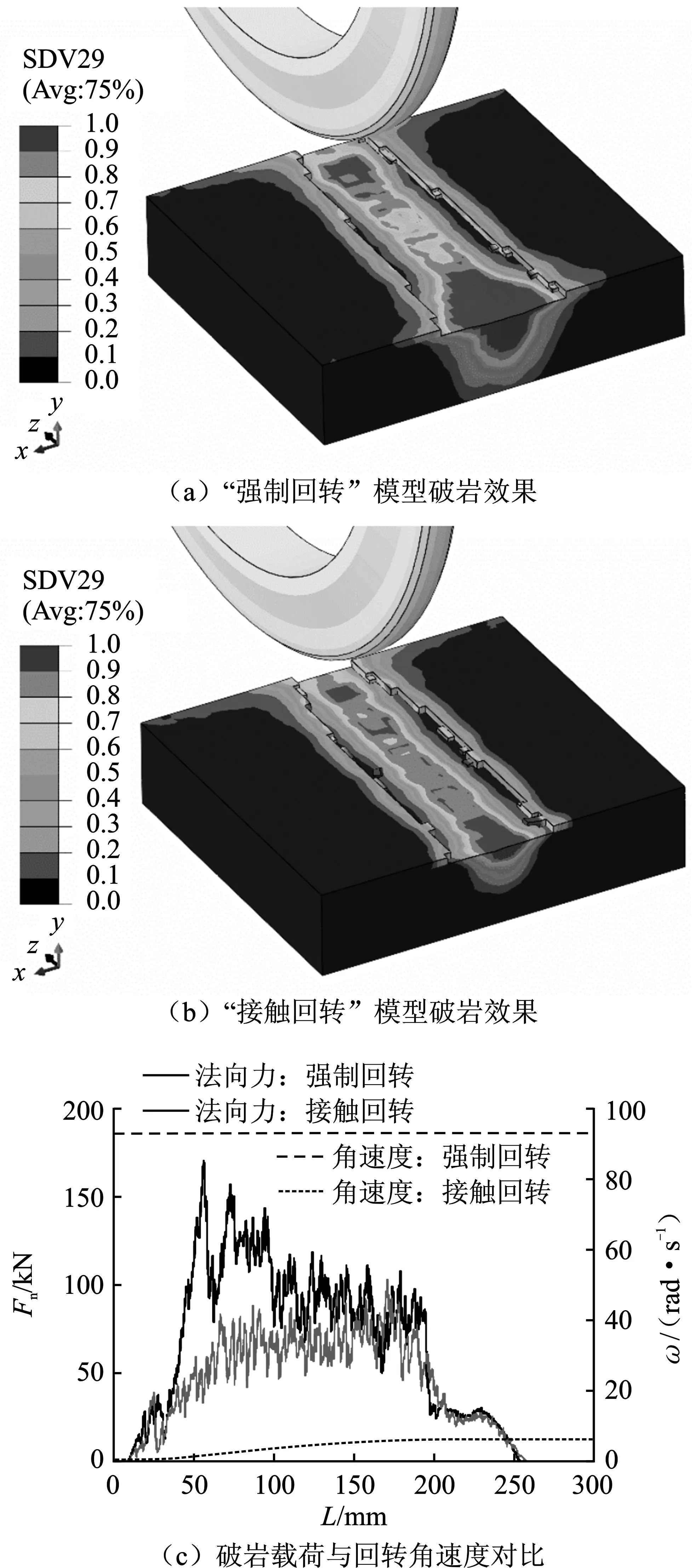
图4 “强制回转”和“接触回转”破岩模拟对比
1.4 数值模型的试验验证
如图5所示,为了验证所建数值模型,开展了双刀顺次回转破岩的数值模拟与试验。数值模型的参数设置如下:岩样厚度为100 mm;刀间距为80 mm;滚刀与岩石侧边的距离为110 mm;外侧(刀1)与内侧(刀2)滚刀的回转半径分别为880 mm和800 mm;2把滚刀绕z轴的公转角速度为29.3 rad·s-1;贯入度为4 mm。破岩试验的参数设置与数值模型一致。受限于所使用的RCM试验台无法分别测试2把滚刀的破岩载荷,因此首先使用外侧滚刀完成30 mm深度的切削后,再行开展内侧滚刀的切削,通过推进系统的推力和驱动系统的扭矩分别换算得到破岩法向力Fn和切向力Ft。如图6、7所示,滚刀1的破岩载荷在前20 m切削时逐渐增大,之后在50~150 kN的范围内波动;滚刀2的破岩载荷明显小于滚刀1,且很多载荷值为0,这是因为滚刀1连续切削了30 mm深度,形成了较深的切槽,并且在岩碴清除后,在岩面上形成了较多凹坑,因此,仅选用滚刀1的破岩载荷用于验证数值模拟结果。试验的平均法向力和切向力分别为104 KN和10 kN,而数值模拟的平均法向力和切向力分别为125 kN和9 kN,两者的误差分别为23%和10%,同时数值模拟的破岩效果与试验结果较为相近,说明所建数值模型基本可用于滚刀破岩研究。

图5 数值模型的试验验证

图6 数值模拟与试验的法向力对比
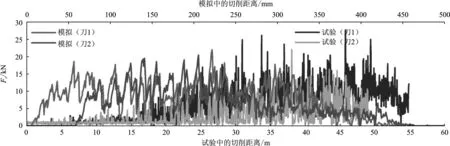
图7 数值模拟与试验的切向力对比
2 结果和讨论
2.1 滚刀破岩效果与载荷分析
选取了64组模拟中的12组代表性破岩结果进行分析(贯入度P=4 mm·rev-1,磨损量W=5~15 mm),如图8所示。对于组合1,当刀刃磨损大于5 mm时,岩石的损伤和破碎效果基本保持不变,这是由于当刀刃磨损大于5 mm时,CCS型滚刀的刃宽基本保持不变;对于组合4,岩石的损伤和破碎效果随着刀刃磨损的增大而增大,这是由于V型滚刀的刃宽随着磨损而线性增大。上述破岩效果可以与破岩载荷(法向力为例)相互印证,如图9(a)所示(图中C表示滚刀编号,如C1表示滚刀1),对于组合1的任一贯入度,当刀刃磨损大于5 mm时,法向力基本保持不变;而如图9(d)所示,对于组合4的任一贯入度,法向力随刀刃磨损增大而线性增大,并且很快超过CCS型滚刀(W>10 mm);上述结果阐释了CCS和V型滚刀的破岩效果差别。对于磨损量较小的V型滚刀,由于其锋锐的刀刃下方容易形成高压力密实核,因而破岩载荷小、破岩效率较高;随着刀刃磨损,刀刃宽度快速增大,破岩载荷迅速增大、破岩效率快速下降。对于CCS型滚刀,因为其刃宽在径向基本保持一致,所以其破岩效率并不随着刀刃的磨损而明显下降。因此,对于某些高硬岩隧道区段,把部分CCS型滚刀替换为V型滚刀,可有效提高破岩效率和掘进速度。

图8 各滚刀组合在不同刀刃磨损量W下的破岩效果(P=4 mm·rev-1)
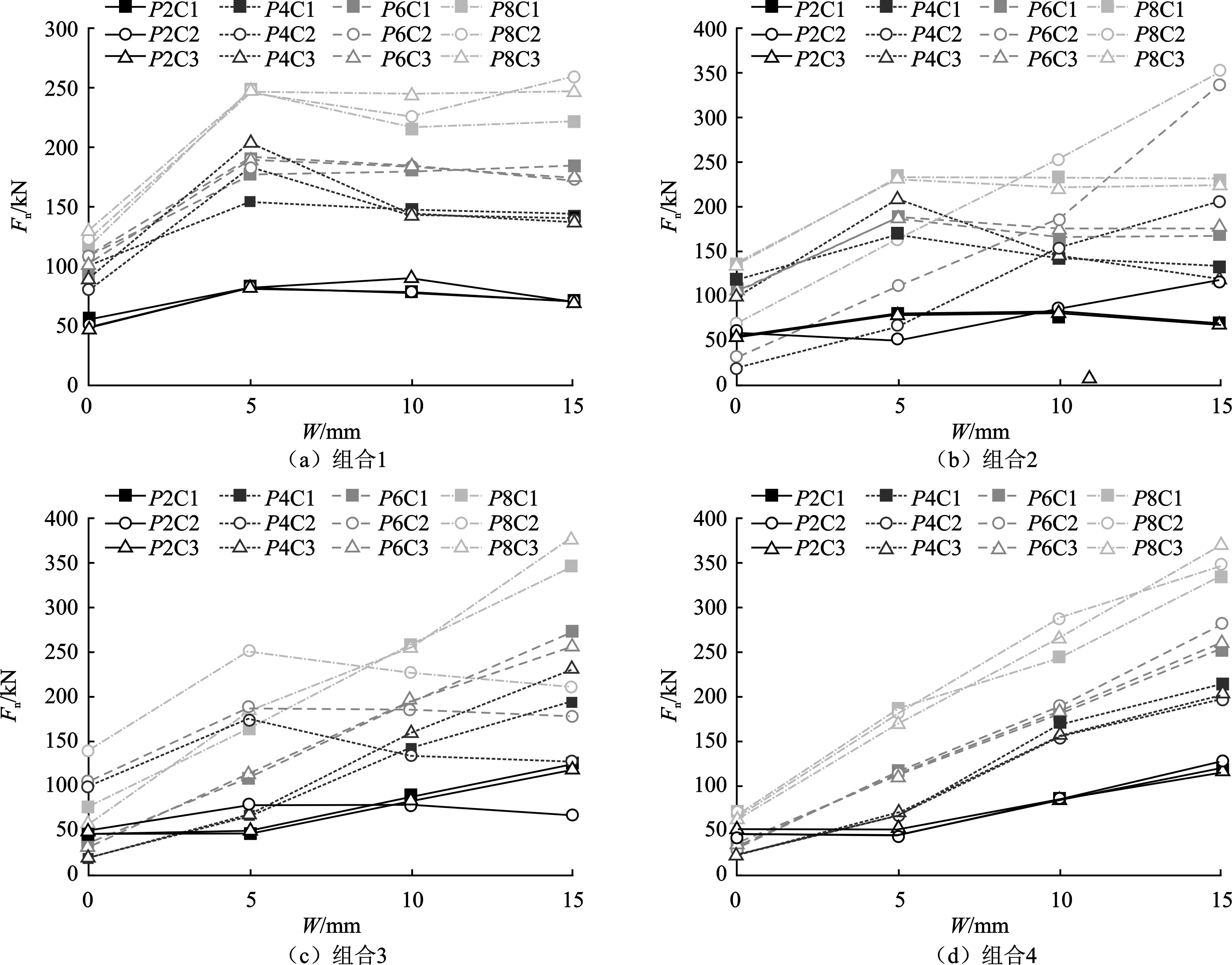
图9 各滚刀组合在不同贯入度P和刀刃磨损量W下的破岩法向力
组合2和3的一个相似结果是:当磨损量W=10 mm时,模型内3把滚刀下方的岩石损伤和破碎效果基本一致,因为此时CCS和V型滚刀的刃宽基本一致,约为20 mm。当磨损量小于10 mm时,CCS型滚刀下方的岩石损伤更为严重,而当磨损量大于10 mm时,V型滚刀下方岩石损伤更严重。上述破岩效果可以与破岩载荷(法向力)相互印证,如图9(b)和(c)所示,当磨损量分别小于、等于和大于10 mm时,CCS型滚刀的法向力分别大于、近似相等和小于V型滚刀。如图10所示(图中CC表示滚刀组合,如CC1表示组合1),对于各个组合内3把滚刀的平均法向力,当刀刃磨损量分别小于、等于和大于10 mm时,各组合的法向力大小分别为“CC1>CC2>CC3>CC4”、“CC1≈CC2≈CC3≈CC4”和“CC1 图10 各滚刀组合内3把滚刀法向力的平均值 上述分析说明,当刀刃磨损约为10 mm,即CCS型和V型滚刀的刃宽相近时(约为20 mm),两者破岩效果相近。因此为了利用CCS和V型滚刀组合以降低破岩载荷、提高破岩效率,刀刃的磨损应该小于某个临界值,处于此临界值的CCS和V型滚刀的刃宽相等。由此推断,对于刃角分别为60°、90°和120°的17 in V型滚刀,刀刃磨损的临界值分别约为17.5、10和5 mm。上述分析也说明,V型滚刀数目越多,对于整体载荷的降低也越明显,但这种载荷降低的效果随着磨损的进行而快速消失。 为了研究不同破岩条件下切向力Fr和法向力Fn的关系,计算了各模型滚刀的滚动系数RC,即切向力与法向力的比值RC=Fr/Fn,图11为各模型中3把滚刀滚动系数的平均值。 图11 各滚刀组合在不同贯入度P和刀刃磨损量W下的滚动系数RC 可以发现,滚动系数随贯入度的增大而增大,这与Balci等的试验研究相吻合,可以通过CSM模型进行理论解释,如图12所示,即与岩石直接接触的刀刃部分(接岩弧)的圆心角随着贯入度的增大而增大。图12(a)中,d表示滚刀直径。 图12 CCS和V型滚刀的滚动系数对比分析 对于不同的贯入度,组合1的滚动系数不随刀刃磨损而明显改变,这是因为CCS型滚刀的刃宽在磨损过程中基本保持不变。对于未经磨损的滚刀,可以发现V型滚刀的滚动系数大于CCS型滚刀(贯入度2 mm除外)。这个结果并不能得到CSM模型理论分析的解释,因为如图12所示,对于不同的贯入度,CCS型和V型滚刀的滚动系数几乎相等;但是这个结果却与学者们的滚刀破岩试验结果相一致。如图12(b)所示,Balci等分别使用未经磨损的CCS型和V型滚刀,在不同贯入度条件下切削了页岩和石灰岩,可以看到滚动系数随贯入度增大而增大,同时V型滚刀的滚动系数明显大于CCS型滚刀。图11同时也表明,随着刀刃的磨损,V型和CCS型滚刀的滚动系数逐渐变得接近,本文从2种滚刀破岩机理的角度对这种现象进行解释。滚刀的破岩主要取决于前端平刃对岩石的碾压作用,因为前端的平刃首先损伤、碾碎并贯入岩石,然后才是其后部的楔刃跟进贯入。因此磨损后的V型滚刀的破岩机理,更类似CCS型滚刀的平刃“碾压”,而不是崭新V型滚刀的“楔形劈裂”破岩,这也使得两者的滚动系数变得接近。 从滚刀破岩效果和破岩载荷可以看到,刀下岩石的损伤程度和破岩载荷随着贯入度的增大而增大,这是由于滚刀与岩石在刀间距方向和滚动切削方向的接触区域宽度随着贯入度的增大而增大。同时,岩石的破碎效果并不随贯入度P的增大而线性地变化,即对于大多数模型,当贯入度P大于4 mm时,滚刀间的岩石已经开始贯通破碎。各组合的破岩比能如图13所示。 图13 各滚刀组合的比能 可以发现,贯入度为4 mm和6 mm模拟的破岩比能明显小于贯入度为2 mm和8 mm的模拟,这是由于2 mm贯入度不足以破碎滚刀两侧的岩石,而8 mm贯入度的破岩载荷过大。上述结果与各国学者通过大量的试验和现场研究所得到的一个结论相吻合,即刀间距与贯入度比值(S/P)的最优取值介于10~20之间。显然,本文2、4、6 mm和8 mm贯入度模型的(S/P)值分别为40、20、13.3和10。对于不同的贯入度,CCS型滚刀的比能基本不随刀刃磨损量而变化,这与工程实际中CCS型滚刀的破岩效率不随刀刃磨损而明显下降的经验相吻合;而V型滚刀的比能随着刀刃磨损而快速增大,而且贯入度越大,这种增大速度越快。当刀刃磨损量小于5 mm、介于5 ~10 mm之间和大于10 mm时,含有V型滚刀的组合(组合2、3、4)的比能分别小于、接近和大于CCS型滚刀的组合1,说明当刀刃磨损量小于10 mm时,把部分CCS型滚刀替换为V型滚刀可以有效地提高破岩效率。 本文通过数值模拟,研究了不同的CCS型和V型滚刀的组合模式、贯入度及刀刃磨损量条件下的破岩过程,主要结论如下。 (1)将部分CCS型滚刀替换成V型滚刀,是提高破岩效率,降低刀盘推力的有效方法;对刀盘推力的降低效果随着V型滚刀数目的增大而提高。 (2)滚刀刃与岩石接触区域的宽度直接影响着破岩载荷和效率。基于此,在使用V型滚刀替换CCS型滚刀时,其刀刃磨损量不应超过某个临界值,V型滚刀处于该临界值时,其刃宽与CCS型滚刀刃宽相等。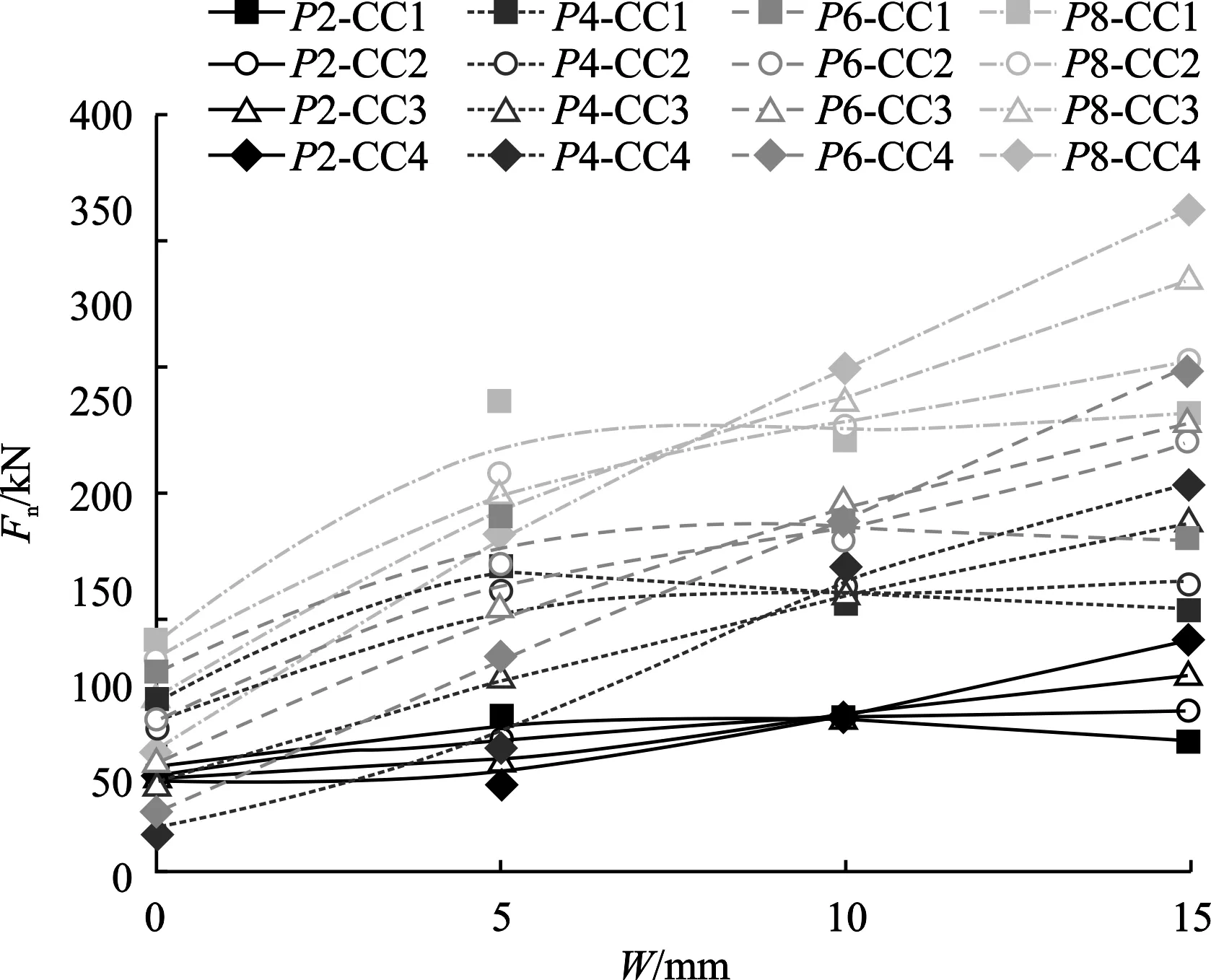
2.2 滚刀滚动系数分析

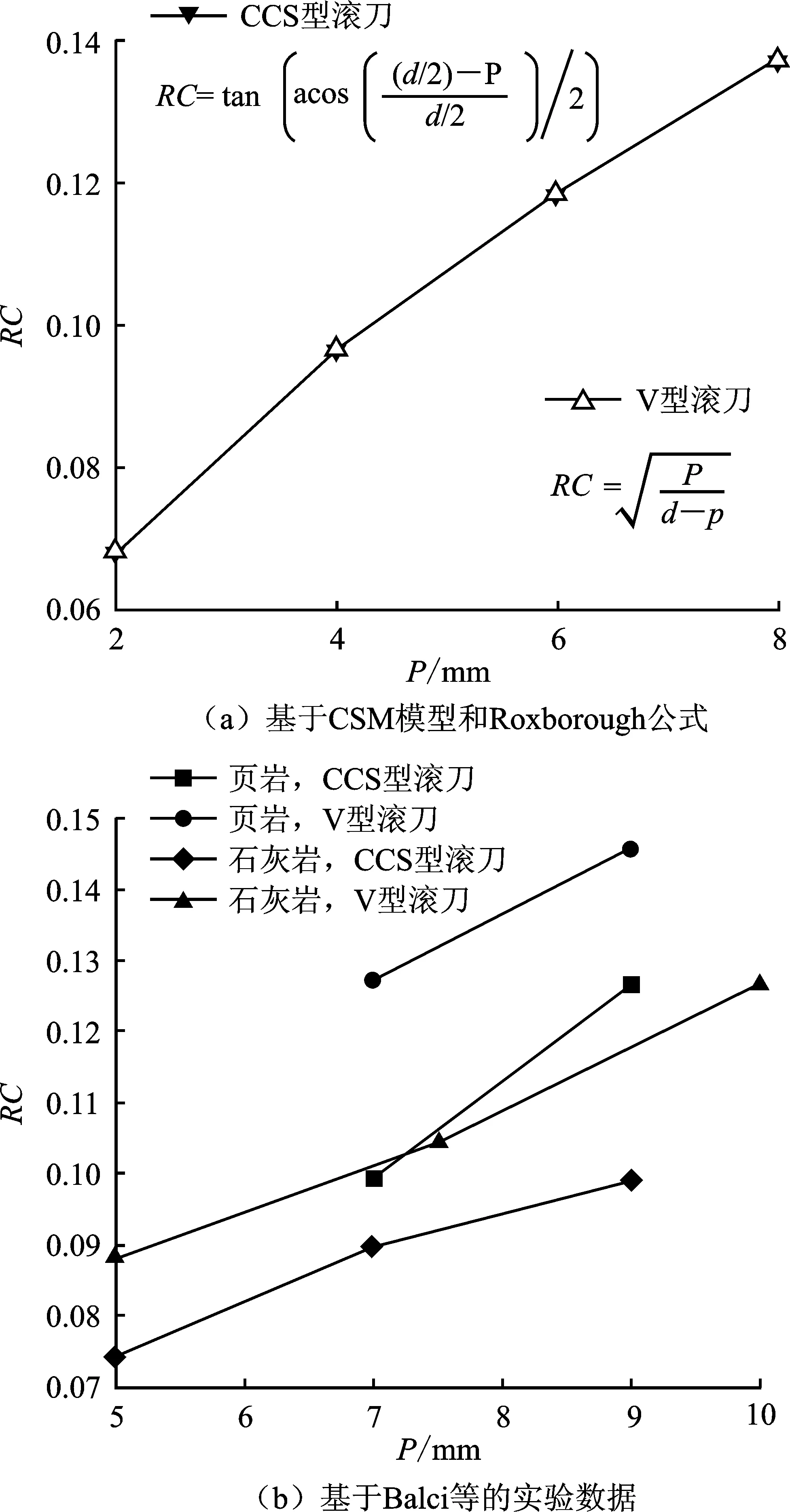
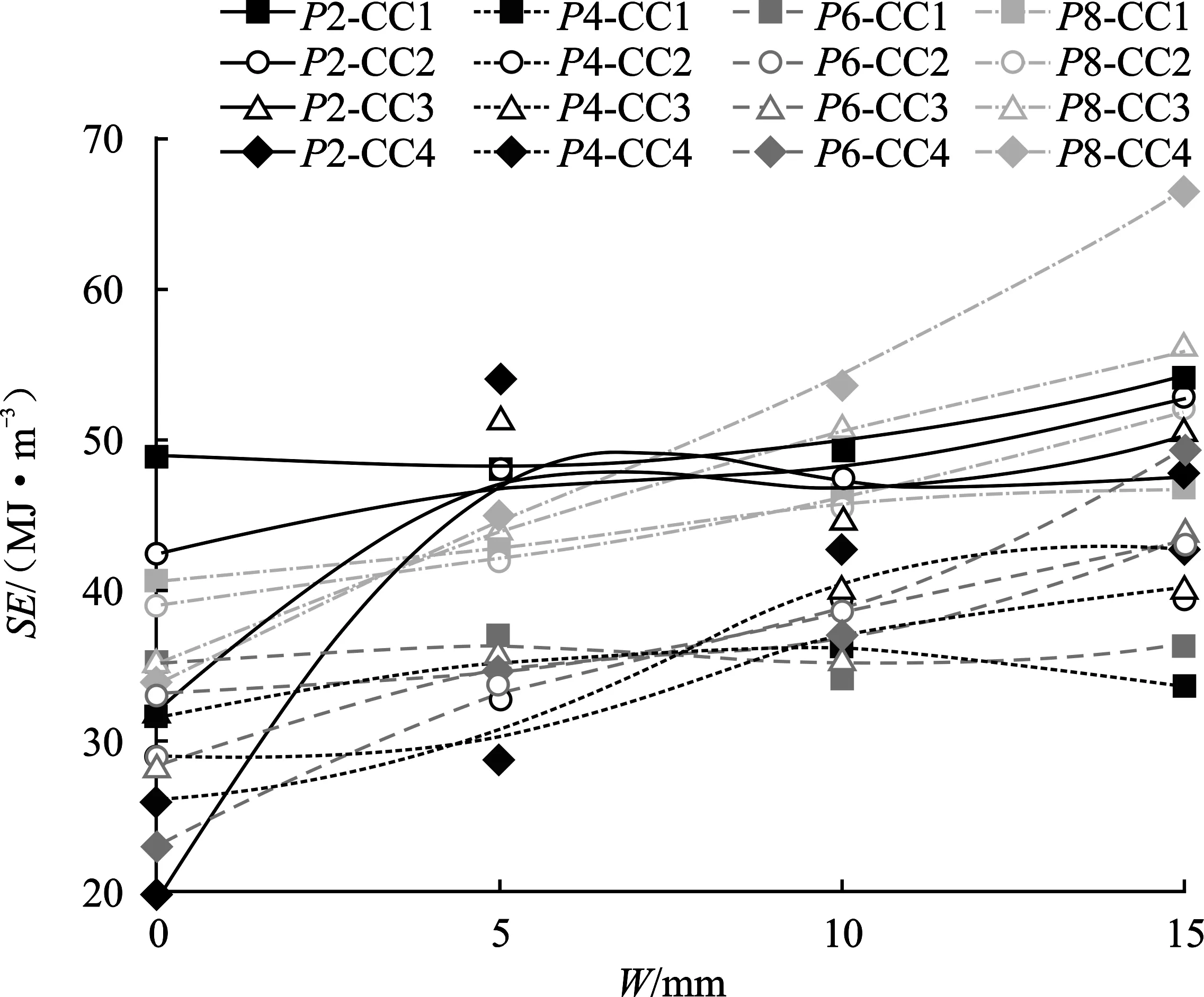
2.3 滚刀破岩效率分析
3 结 语
——分清“主”和“次”

