悬索桥塔梁约束条件的设计与研究

刘金朝，王惠民，姚 激，黄 坤，兰玮琦，韩团齐

(1.昆明理工大学 建筑工程学院，云南 昆明 650500； 2.云南泽惠工程造价咨询有限公司，云南 昆明 650021)

0 引 言

21世纪以来，随着中国经济的发展、技术的创新、新材料的产生和设计理论的完善，桥梁的形式和跨径都在不断地增加[1]。悬索桥以其大跨越能力和美观性能，有着其独特优势。而随着悬索桥的不断发展，大跨径悬索桥的静力稳定性问题和动力学问题也日益突出[2-4]。

国内外学者对传统的大跨度悬索桥的静力性能和抗震性能已经开展了不少研究[5-12]，胡世德等对江阴长江大桥提出在建立动态时程分析的基础上，着重进行了纵向地震反应分析；黄康以某座长江大桥为例研究了地震行波效应分析；李楚鹏研究了桩-土共同效应对人行悬索桥自振频率的影响以及地震输入方向对于地震时程分析的影响；师新虎等以桥梁抗震细则规范的设计反应谱为目标谱，采用一定的方法拟合与目标谱相匹配的人工地震波；悬索桥不同的设计参数以及约束条件对于其本身的受力性能有着很大的影响。

在以往的研究中一般探讨垂跨比对悬索桥受力性能的影响，对于塔梁约束条件的研究相对较少[13-14]。针对悬索桥的受力分析，塔梁之间的约束条件也是一个重要的影响因素[15-16]。本文以某实际项目为例，建立了桥梁有限元模型，对悬索桥进行静力和动力性分析，得出3种塔梁约束体系下悬索桥的自振频率及其静动力的响应，探讨塔梁约束条件对悬索桥力学性能的影响。

1 有限元模型

本项目悬索桥的跨径为(125+600+125)m，主梁采用扁平钢箱梁，主塔采用C40混凝土。悬索桥垂跨比为1/10，其形式为地锚式悬索桥。采用有限元分析软件midas Civil建立桥梁有限元数值模型，如图1所示，模型的x方向为纵桥向，y方向为横桥向，z方向竖向。梁单元72个，只受拉单元202个，总节点281个。模型的边界条件：桥塔底部和主缆锚固点采用一般支承，约束全部方向；塔顶与主缆之间采用刚性连接，释放x方向约束；塔梁处的约束条件为3种：固结、漂浮、一般支撑。表1为悬索桥主要构件的参数。

图1 悬索桥有限元模型

表1 悬索桥主要构件的参数

为了研究悬索桥塔梁约束对悬索桥的影响，研究保持悬索桥的垂跨比、边跨比等因素不变，采用控制变量法，仅改变塔梁约束。对建立的悬索桥进行数值模拟研究。

2 悬索桥塔梁约束对静力特性的影响

2.1 成桥状态下约束条件对主梁弯矩的影响

对悬索桥模型进行分析计算，在不同的塔梁约束条件下，成桥状态的悬索桥的主梁弯矩如图2所示。

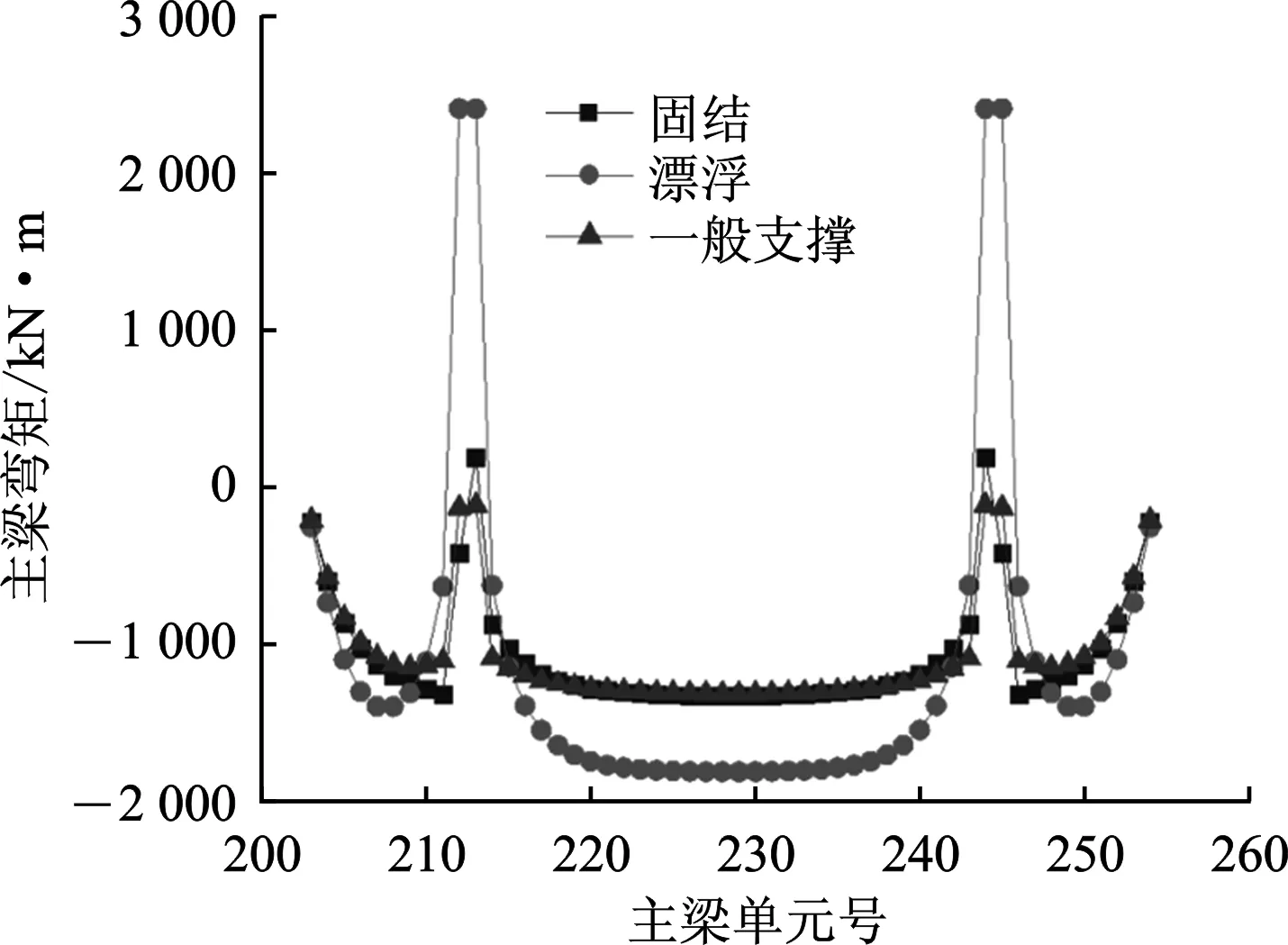
图2 悬索桥主梁弯矩

由图2可知，漂浮体系在塔梁支撑处，主梁正弯矩较大，这表明主塔处的约束条件对弯矩有较大的影响。固结和一般支撑体系，在此处主塔有支撑点，而漂浮体系由于靠近主塔的附近没有任何支撑点，且吊杆力在此处也相对较大，故弯矩较大。但是在主跨节段时，整个漂浮体系的主梁弯矩值又小于其他2种体系的主梁弯矩值。

2.2 成桥状态下约束条件对吊杆力的影响

图3为成桥状态下，在不同塔梁约束条件下的悬索桥吊杆力。

图3 悬索桥吊杆力

由图3可知，在成桥状态下，漂浮体系在塔梁支撑处附近的吊杆力显著增大。这是因为漂浮体系在塔梁处没有承担主梁的支撑点，固结和一般支撑在此处会由主塔承担部分主梁质量，而漂浮体系则全部由靠近主塔的2根吊杆承担。因此，漂浮体系的吊杆力约为其他2种体系的吊杆力的1.5倍。对于计算模型，漂浮体系在主塔附近的9号吊杆为最大值，固结体系和一般支撑体系分别为608.39、610.83 kN。漂浮体系的最大值为864.61 kN，分别是固结、一般支撑体系的1.42倍、1.415倍，与理论计算值基本接近。

2.3 成桥状态下约束条件对主缆应力的影响

图4为成桥状态下，在不同塔梁约束条件下的悬索桥主缆应力。

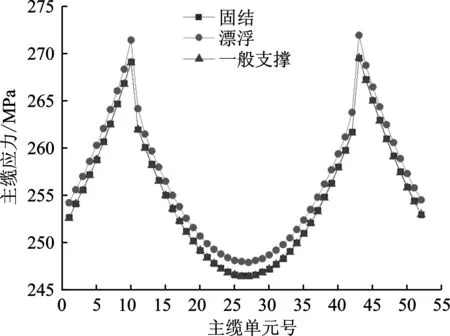
图4 主缆应力

由图4可知，在成桥状态下，3种约束条件下的悬索桥主缆应力分布基本一致。采用漂浮体系时，由于在塔梁连接处没有支撑，主梁所有的质量均由吊杆承担，最后传递给主缆。在成桥阶段，漂浮体系吊杆力稍微大于其他2种体系，其主缆应力也略微大于其他2种体系。

3 自振特性

自振特性是桥梁结构的固有特性。对桥梁结构的自振特性进行研究，也是对其进行动力响应分析的基础[17-19]。本文利用midas Civil有限元软件提取了3种塔梁约束条件下模型的前十阶频率，其计算结果如表2所示。

由表2可知，漂浮体系的前三阶频率分别为0.135 6、0.163 9、0.225 2 Hz，为3种体系中频率最小；固结体系的前三阶频率分别为0.233 5、0.248 7、0.279 9 Hz，为3种体系中频率最大。固结体系的前三阶频率比漂浮体系的前三阶频率分别增大了39.9%、8.9%、13.5%。结构的自振频率仅与其质量、刚度相关。3种不同约束体系下的模型质量相同，因此，模型的自振频率主要受到结构本身刚度的影响。固结时，桥梁的刚度最大，其自振频率也是三者中最大的，其次为一般支撑，而漂浮体系的刚度最小，因此自振频率也是三者中最小的。

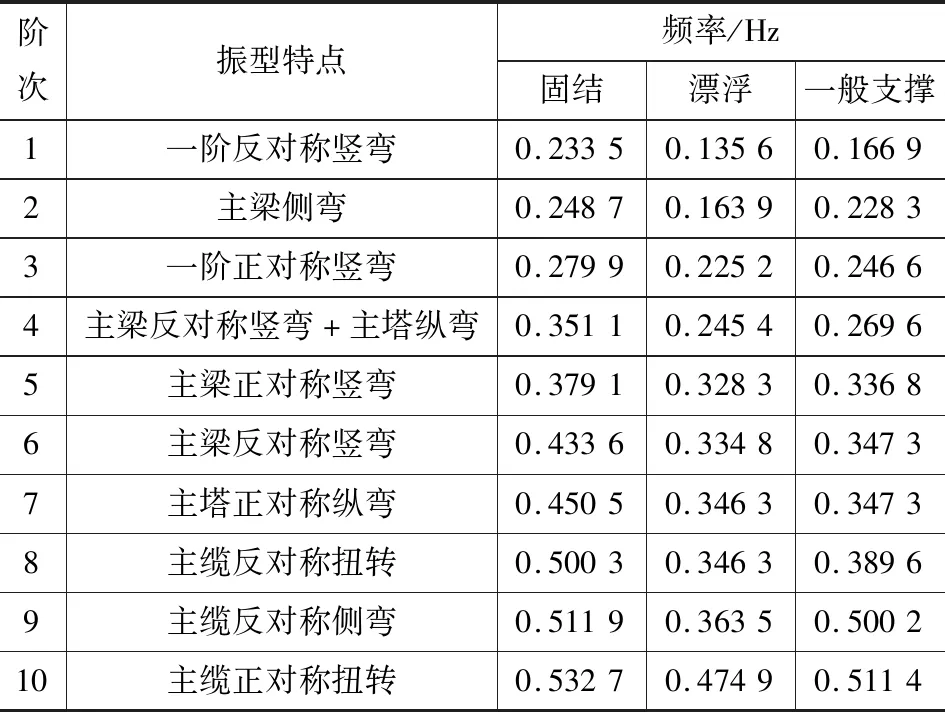
表2 前十阶自振频率

4 悬索桥塔梁约束对动力响应的影响

根据《公路桥梁抗震设计细则》可知，选择3条经典波(Elcent、Taft、Sanfer)输入[20]，根据桥址抗震设防烈度的要求，将所选3条地震波的峰值调整为0.1g，由于该悬索桥的空间对称性，仅考虑沿纵桥向的水平地震动输入。由《公路悬索桥设计规范》第6.4.4条可知：当采用3组地震加速度时程时，最终结果应取各组结果的最大值。计算结果表明：在Taft波作用下，模型的动力响应值最大。限于篇幅，本文仅给出Taft波计算结果。调整过后Taft波的时程数据如图5所示。

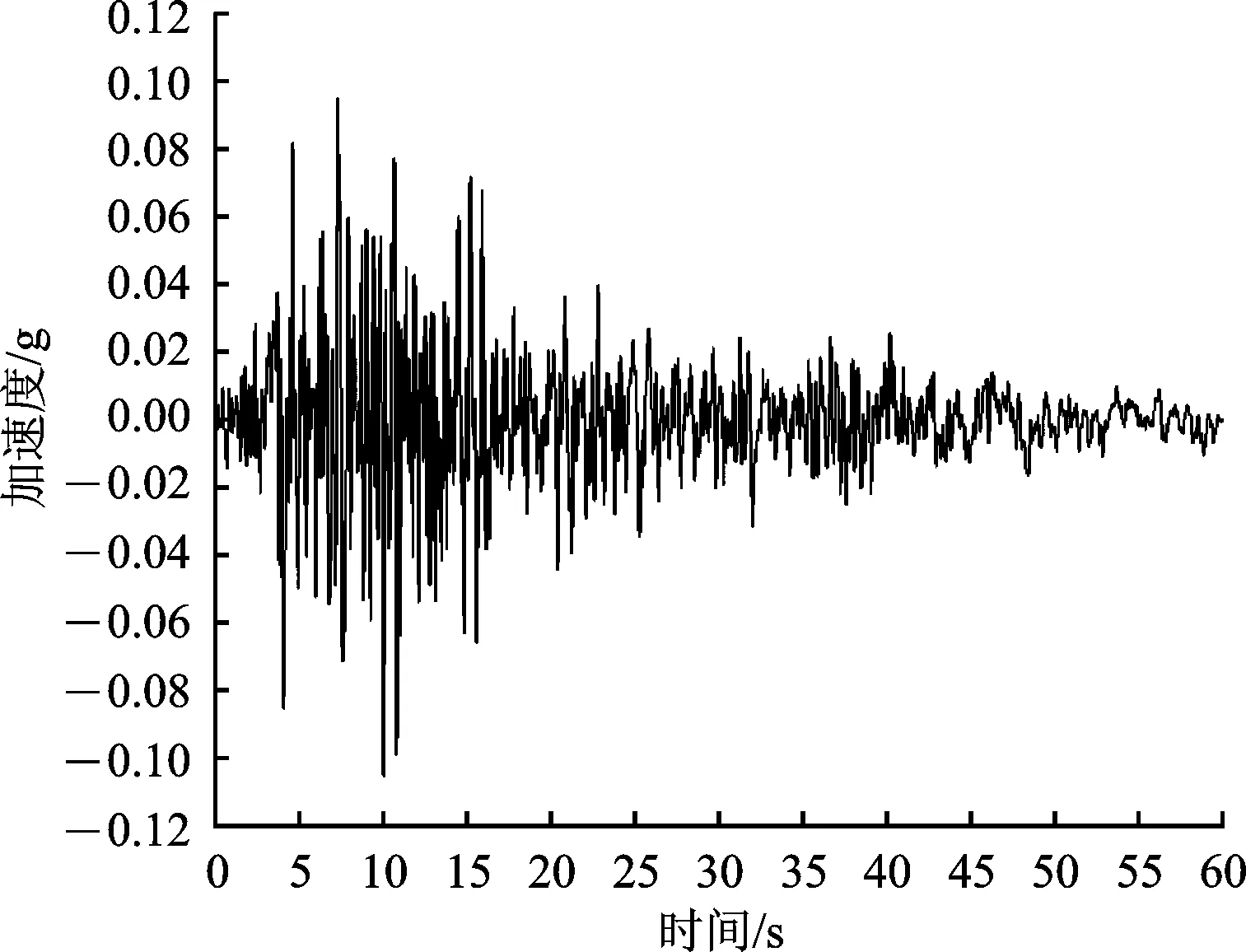
图5 调整后的Taft波

地震作用时，在3种约束条件下，主梁梁端纵向位移如表3所示，塔梁约束条件为固结时的纵向位移最小，另外2种体系的纵向位移均相差不大，分别为128、111 mm。

表3 主梁纵向位移

固结体系时的主梁竖向位移最大值也是最小的。竖向位移大小及其位置分别为：固结体系在边跨中部，最大位移为25 mm；漂浮和一般支撑体系均在主跨1/4处，且分别为86、76 mm。

塔梁之间的相对位移见表4，因为塔梁连接为固结体系时主塔和主梁是同步的，所以相对位移最小，仅为2 mm。而漂浮和一般支撑体系则会产生一定的位移，约为100 mm左右。

表4 塔梁相对位移

由表5可以知道，在水平地震波作用下，固结时塔底将会产生较大的弯矩，对结构受力十分不利，漂浮和一般支撑条件下塔底的弯矩值比较接近，其值分别为固结时的72.87%、72.81%。

表5 塔底弯矩

由表6可知，漂浮、一般支撑体系的塔底剪力为751.87、752.08 kN，而固结体系则增大到1 383 kN，为漂浮、一般支撑体系的183.94%、183.89%。

表6 塔底剪力

从表3～6可知：在地震作用下，虽然固结体系的悬索桥位移值较小，但是其塔底弯矩和剪力均较大，对结构安全不利。

5 结 语

大跨度悬索桥的垂跨比和塔梁约束体系都会对桥梁有较大的影响，依托某实际工程对悬索桥的塔梁约束体系进行了研究，采用有限元软件建立桥梁模型进行分析，主要结论如下。

(1)在漂浮体系下，由于缺少支撑点，主梁质量全部由吊杆来承担。悬索桥在塔梁连接处附近的2根吊杆会受到较大的力，其值约为其他2种约束体系的1.5倍，并且悬索桥主梁在此处也会产生较大的主梁正弯矩。

(2)虽然固结体系在地震作用下的位移响应较小，但是主塔底剪力和塔底弯矩比其他2种体系更大，弯矩分别比漂浮体系和一般支撑体系增大了37.23%、37.35%，剪力增大了83.94%、83.89%。因此地震作用下固结体系的地震响应较为明显。

(3)综合考虑有限元模型分析中的静力分析和动力分析得出的结果，一般支撑体系对于本悬索桥有更好的效果和更好的受力性能，对结构更加有利。