应用坐标式三角形面积公式求解竞赛题

浙江省金华市第六中学 (321000) 虞 懿

1.坐标式三角形面积公式

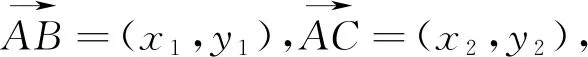
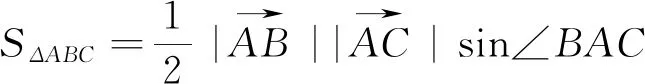
此公式乃坐标式三角形面积公式，其形式与平面向量共线的充要条件的坐标公式特征极其相似，下面通过具体的实例来说明这一面积公式在数学竞赛题中的应用，旨在探索解题规律，揭示解题方法．

2.应用举隅

2.1 求三角形面积之比

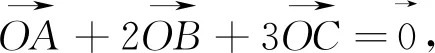
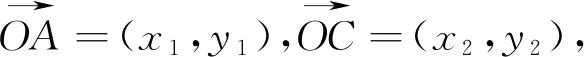
评注：三角形面积的坐标表示与向量的坐标表示达成了完美的统一，可将几何问题转化为代数问题求解．

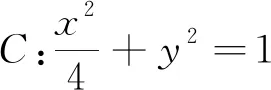
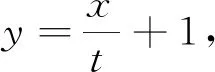
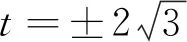
评注：对于圆锥曲线中的面积问题，运用坐标式三角形面积公式则更能体现思维与运算的优化．

2.2 求三角形面积

评注：本题借助坐标式三角形面积公式及用椭圆的参数方程形式表示椭圆上的点的坐标，将已知条件转化为三角函数求值问题，避免了复杂的运算．

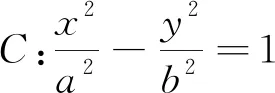
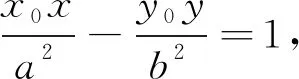
评注：解析几何问题的本质是用代数方法解决几何问题，坐标式三角形面积公式自然地提供了解决解析几何中有关三角形面积问题的一条捷径．

2.3 求三角形面积的最值(取值范围)

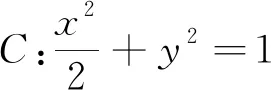
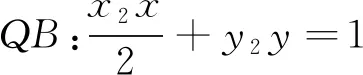
故点Q的轨迹方程为x+y=2.

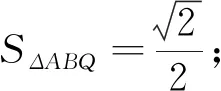
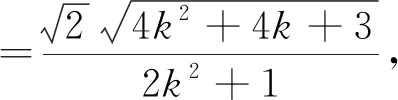
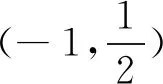
评注：借助坐标式三角形面积公式来求解三角形面积问题，可以避免对夹角和边长的计算，也避免了对平面图形的分割，让学生感悟数学问题的简洁美与对称美．

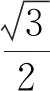
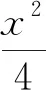
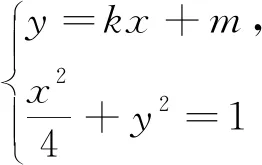
所以ΔOPQ面积的取值范围为(0,1)．

评注：利用坐标式三角形面积公式求解关键在于确定三角形各点的坐标．对于求解方程比较困难(方程的根不是十分简便)或含字母参数时可利用根与系数的关系进行合理转化．

纵观上述几例，应用坐标式三角形面积公式来解决三角形面积问题，由于在解题过程中避免了求边长和该边上的高两个步骤，因此使解题过程变得简洁，这对优化学生的思维品质，提高学生的解题能力是大有益处的．