基于分布参数模型的互联电力系统输电线路故障定位

刘晓琴，李 强，孙海军，刘 璐

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

在当今竞争激烈的电力市场中，输电线路故障的准确定位对于电力系统的经济运行具有非常重要意义。准确可靠的故障定位方法和技术可以减少维护人员巡线工作量，加快故障修复速度，减小停电损失，保障电力系统的安全经济可靠运行。故障分析方法按照输电线路模型分为集中参数模型和分布参数模型；按照定位原理分为利用工频量的传统阻抗法和利用暂态行波的行波法；按照测量电气数据的来源可分为单端法和双端法，利用故障线的一端或双端进行测量。双端方法只要求对故障传输线进行精确的建模，而不需要任何简化的假设[1-12]，但是需要使用 GPS[9，11]或一些计算技术[10]在线路两端之间进行时间同步。单端方法不需要线路两端之间的通信[13-19]，却需要对故障传输线和嵌入式学习线路的电力系统进行数学建模分析，通常可以简化分析问题。电力系统模型有关的不确定性以及运行条件的变化，在忽略部分影响因素的前提下，传统单端法的测量精度低于双端法。然而，单端法测量可节省成本，操作简单且易于实现。因此，深入研究单端测量法对电网故障定位技术的发展具有重要意义。

本文提出一种基于分布参数模型的单端故障定位方法，适用于n母线互连电力系统中的架空输电线路。为了提高故障定位精度，该方法采用传输线的精确分布参数模型和电力系统一种双母线等效戴维宁网络模型，并进一步解释了系统的互连性。通过对11母线互联电力系统的仿真得到了暂态故障数据，验证该方法的准确性。

1 故障定位方法

考虑一个通用的n母线电力系统，在F点处发生短路故障，P母线和Q母线通过输电线路相连，一种具有故障传输线的通用n母线电力系统如图1所示。双母线戴维宁等效网络电力系统如图2所示。

图2 双母线戴维宁等效网络电力系统

阻抗ZPP、ZQQ和ZPQ是系统正序母线阻抗矩阵Zbus的 PPth、QQth和PQth元素。电压源值VP0和VQ0分别表示母线P和Q的故障前正序电压。ZPP为局部母线阻抗，ZQQ为远端母线阻抗。应该注意的是，由于分析时不包含故障线路，且只需要正序等值网络，应将图2所示的模型用于电力系统的故障定位研究，两条单母线戴维宁等值网络电力系统如图3所示。

图3 两条单母线戴维宁等值网络电力系统

图3所示的电力系统模型是由两个单母线的戴维宁等值网络组成的，其含义为故障线路是P母线和Q母线之间的唯一连接线路。同理，如果这条线路被移除，系统将会被分成两部分，这与电力网络中的互联系统的实际情况不一致。因此，利用图2的模型更能明确地阐述电力系统的互联性。

文献[17]的电力系统模型采用了双母线戴维宁等值网络模型，故障线路采用了分布式参数模型，但采用了与本文不同的方法。本文采用了一种精确的故障线路分布参数模型，相对于简单的集总参数模型，考虑了并联电容的作用。

1.1 对称故障

假设图3中F处的故障是三相对称故障，故障线路特性由A、B、C、D四个参数来表示，故障线路分布参数模型如图4所示。线路总长为l，假设在点F处发生故障，故障距离为x。

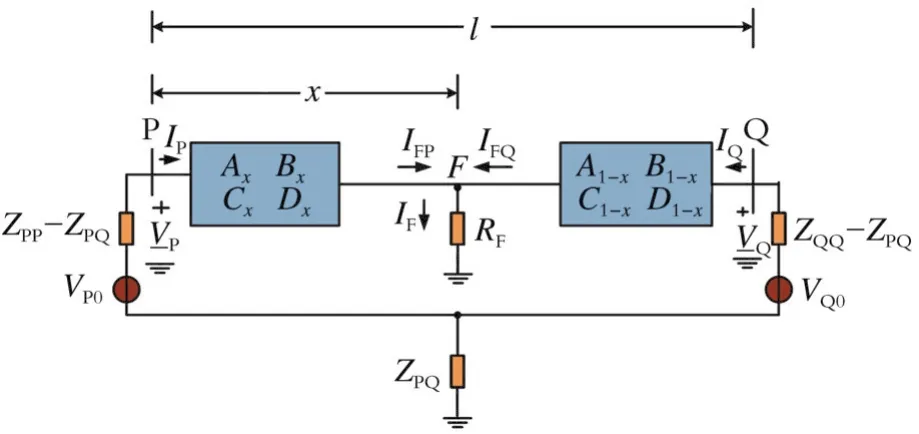
图4 故障线路分布参数模型

长度为l的一般线路的参数为：

式中，γ、ZC分别为线路的传播常数和特征阻抗，其计算公式为：

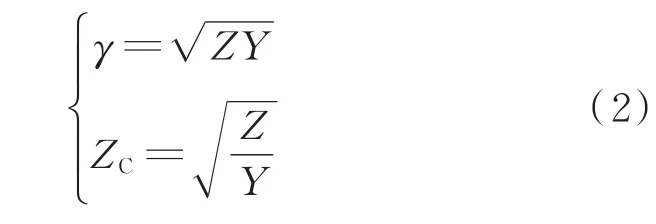
式中，Z为直线单位长度的正序列串联阻抗；Y为线路单位长度的正序并联导纳。故障点F处的电压为：

式中，VP为故障期间在母线P上测量的正序电压，kV；IP为故障期间在母线P上测量的正序电流，kA。

可知：

式中，RF为故障电阻，Ω；IF为故障电流，kA。

把式（3）和式（4）联立可知：

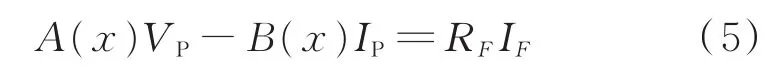
将式（5）的两边乘以I*F(故障电流的共轭复数)，得：

取式（6）两边的虚部，假设RF是实数，得：

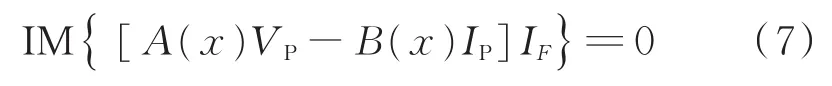
故障电流IF是未知的，但可以用故障距离x来表示。上述方程组复数根的求解利用了文献[20]提出的方法。

叠加元件电路(纯故障等效电路)如图5所示，用于计算母线P和Q因线路发生故障引起的电压和电流的变化。

图5 叠加元件电路(纯故障等效电路)

从图5可知：

式中，VP0为母线P处的故障前的正序电压，kV；IP0为母线P处的故障前的正序电流，kA。

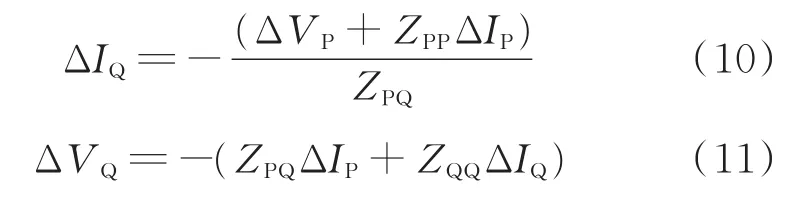
式中，ΔVP为母线P处电压的变化；ΔIP为母线P处电流的变化；ΔVQ为母线Q处电压的变化；ΔIQ为母线Q处电流的变化。根据ΔVP和ΔIP和电力系统正序阻抗矩阵中的阻抗参数ZPP、ZQQ和ZPQ来计算电压下降的数值[21]。

从图5可知，故障电流IF的计算公式为：

式中，IFP和IFQ分别为母线P和Q输入的故障电流，kA。其计算公式为：

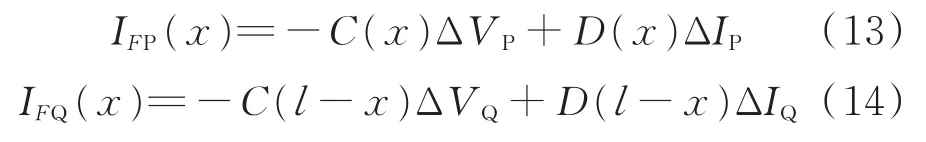
把式（12）—（14）故障电流的值代入到式（2）中，得到了一个形式为f(x)=0的非线性方程，其中唯一未知的是故障距离x。这个方程可以用改进欧拉法、多步法、龙格-库塔法进行数值求解。

1.2 不对称故障

对于不对称故障，采用三相分布参数模型求解故障线。在该模型中，线路的A、B、C、D参数为3×3矩阵。

式中，γ、ZC为3×3阶矩阵，计算公式为：

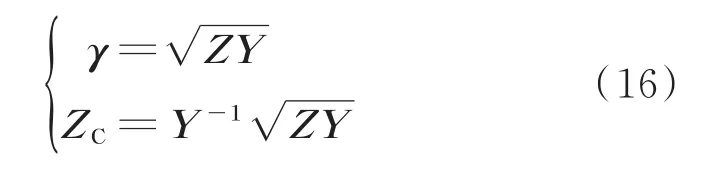
式中，Z、Y分别为线路单位长度的串联阻抗矩阵和并联导纳矩阵。

1.2.1 单相接地故障 假设在F点处有a相接地故障，给出故障点F处的a相电压为：

通过式（18）得到的VFa值代入式（17），乘以取双方的虚部，可得：

故障电流IFa的a相可以使用图5所示的叠加元件电路和式（10）-（14）以故障距离x的形式来表示，则式（8）和式（9）表示为：

式中，ΔVPa、ΔIPa分别为母线P上因故障引起的a相的电压和电流的变化；ΔVPZ和ΔIPZ分别为母线P上因故障引起的零序电压和电流的变化。这里的变化是指故障期间值的大小和故障前的值大小之间的差异。零序电压和电流由母线P处测量的三相电压和电流来计算。式（19）可以对故障距离x进行数值求解。

1.2.2 两相故障 假设在F点发生b相和c相间故障。给出了故障点F处b相电压和c相电压的差值的两种计算公式为：

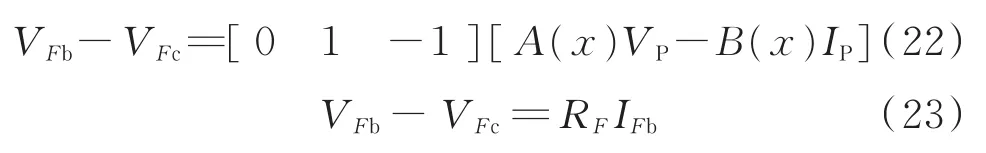
联立式（22）和式（23）乘以I*Fb，然后对两边分别取虚部，可得：

同理，b相故障电流IFb可以使用图5中叠加元件电路和式（10）—（14）以故障距离x的形式来表示，式(8)和式(9)必须改为：

式中，ΔVPb、ΔIPb分别为母线P上的b相电压和电流由于线路故障而产生的变化量。如果输电线路不换位，则利用b相和c相电压和电流变化的平均值，可以得到较好的效果。

式中，ΔVPc、ΔIPc分别为母线P由于故障引起的c相电压和电流的变化。

1.2.3 两相接地故障 假设在F点发生b相和c相接地故障，故障点F处b相电压和c相电压的差值的计算公式同式(22)。两相接地故障和两相间故障不同的是两相接地故障下式(22)的差等于0。即:

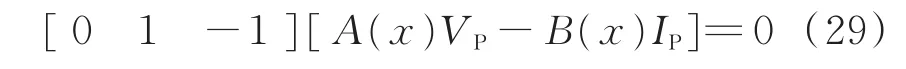
式(29)可以对故障距离x进行数值求解。

2 实验研究

11母线互联电力系统接线图如图6所示。

图6 11母线互联电力系统接线图

图6中1-11分别表示系统中不同位置的母线，G1—G3表示系统中的同步发电机，T-1、T-2、T-3表示系统中的变压器。该方法测试了故障定位的精度和对电力系统模型参数误差的敏感性。发电机、变压器、输电线路长度及参数和负荷参数见表1—5。

表1 发电机组参数

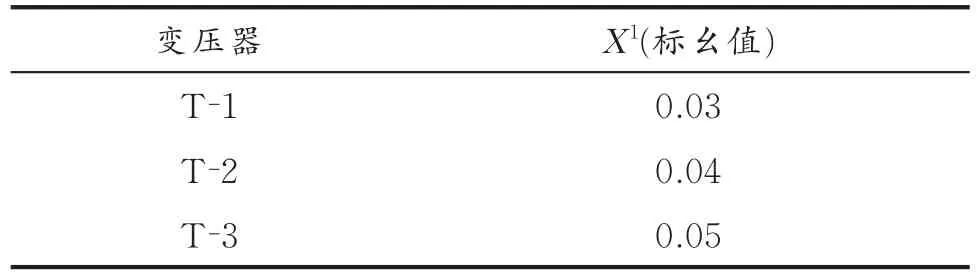
表2 变压器组参数

表3 输电线路长度

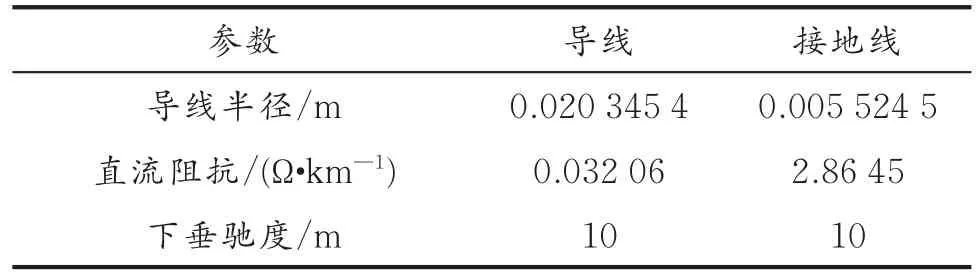
表4 输电线路导线和接地线参数

表5 负荷参数

电力系统元件的阻抗数据见表6。所有变压器均为100 MVA，23/230 kV变压器11-7通过标幺值为0.08的电阻接地。所有的传输线都是不换位的。

表6 系统元件阻抗数据

利用MATLAB软件，用阻抗数据构建节点导纳矩阵（Ybus）和节点阻抗矩阵（Zbus）。利用这些函数之一建立了系统的正序导纳矩阵，然后利用MATLAB矩阵求逆得到了系统的正序阻抗矩阵。Z母线的阻抗ZPP、ZQQ和ZPQ所求得的数值见表7。

表7 系统正序阻抗矩阵参数

利用MATLAB软件对系统进行仿真。假设有一条230 kV、200 km的故障线路连接母线6和8。在距离母线6不同距离处分别考虑不同类型的故障。故障定位器使用了6母线上可供测量的全部数据。电压和电流相量的计算采用了改进的全周期傅里叶算法，包括直流量偏移消除。

故障定位计算在MATLAB软件中进行。用MATLAB 函数 fzero（）求解式（7）、式（19）和式（24）。该函数采用二分法、割线法和可逆二次插值法相结合的方法。但是，因为式（29）不是实数值，所以不能通过fzero（）求解。可以通过MATLAB函数fminserch（）求解其最小值，该函数采用直接单纯形搜索法。

2.1 准确性分析

故障定位方法的精度如表8所示，表8给出了针对不同类型的故障、实际故障距离和故障电阻计算测得的故障距离。使用计算故障距离和实际距离差的绝对值除以线路全长，即故障距离的误差（E）可用式（30）计算：

式中，xcom为计算的故障距离；xact实际的故障距离；L为线路实际长度。从表8可以看出，所提方法可以对所有类型故障的故障距离进行高精度的估计，测量的故障线路的电阻值可达50 Ω。在测试故障定位算法的准确性时，百分比误差是根据总线路长度计算的，而不是针对正确的故障距离计算的，这是一种常见的做法，因为输电线路维护人员查找故障距离的总长度即为线路全长。

表8 故障定位方法的精度

这种情况下的最大误差约为0.5%，从6号母线到接地故障的线路距离为50 km，故障电阻为50 Ω，这相当于一个大约1 km的绝对误差。当故障电阻增加到非实际的较高的值100 Ω和200 Ω时，单线接地故障和两相相间故障的误差较大，约为2.0%。然而，三相故障和两相接地故障仍然可以维持较高的精度。

故障距离误差源自于方法推导过程中的两个假设。第一个假设为故障阻抗是纯阻性的，但此假设不应在此引入任何误差，因为MATLAB模拟中使用的故障阻抗也是纯阻性的。第二个假设是隐含的。当使用对称分量法推导故障定位公式时，假定系统中的故障传输线和其他线路是可以完全换位的，但是MATLAB模拟中使用的所有线路都没有换位，这将在计算故障距离时引入误差。值得注意是，在推导两相接地故障的定位公式时，未使用对称分量，是这种类型故障的故障定位误差较低的原因。由于故障线路参数不准确，电力系统参数不准确，利用暂态电压和电流信号计算基频相位带来其他误差。

2.2 参数误差的敏感性分析

本文使用的电力系统参数是从系统的正序阻抗矩阵Zbus中得到的阻抗ZQQ、ZPQ和ZQQ，这些阻抗中的任意一个在其幅值和相位角上都可能存在误差。为研究所提方法对这些误差的敏感性，考虑一个单相接地故障，距离母线6的距离为150 km，其故障电阻为10 Ω。在各阻抗ZPP、ZPQ和ZQQ的幅值和相位角中引入了高达±50%的误差。也就是被测参数的正确值被替换为故障定位计算中的错误值，并观察计算出的故障距离产生的误差。

文献[22—23]分别提出了传统的单端故障定位方法和一种双端故障定位方法，与本文提出的单端故障定位方法在相同实验条件下进行仿真对比。三种故障定位方法的相对误差如图7所示。

图7 三种故障定位方法的相对误差

从图7可以看出，在不同的故障距离下，与传统单端定位方法相比，本文提出的故障定位方法，相对误差显著减小，具有明显优势。30 km故障距离下相对误差减小58.23%，而150 km故障距离时相对误差减小79.36%，故障定位的精度得到了明显的提高。且随着故障距离的增大，故障定位精度也越来越高；相对于双端法，本文提出的故障定位精度也有一定的提高，在故障距离30 km的相对误差减小18.78%，150 km故障距离时相对误差减小20.26%。不同短路类型下故障定位方法的相对误差如图8所示。

图8 不同短路类型下故障定位方法的相对误差

从图8可以看出，不同的故障类型下，无论是三相短路的对称故障，还是单相接地短路、两相短路、两相接地短路的不对称故障，本文提出的故障定位方法相对于传统单端定位方法，相对误差均有明显的减小，故障定位的精度得到明显的提高。相对于双端法，在不同的故障类型下，其故障距离的相对误差也有一定程度的减少。

为了保证故障定位的高精度，局部阻抗ZPP幅值和相位角都必须是准确的。然而，ZPP、ZQQ和ZPQ三种阻抗都是从电力系统的正序阻抗矩阵Zbus中获得。因此，必须使用一种随故障变化而变化的Zbus，确保真实地反映故障期间的电力系统状况。本文方法与文献[16]提出的方法不同，完全避免了使用零序Zbus，以及与之相关的所有不确定性。

3 结 论

针对n母线互联电力系统中的架空输电线路，提出了一种新的单端故障定位方法。该方法利用了故障前和故障期间从故障线路一端测得的电流和电压的相量值，实现高精度的故障定位。该方法对故障传输线采用了精确的分布参数模型。对n母线电力系统使用了双母线戴维宁等效网络模型，该模型解释了n母线电力系统的互联性。该方法所需的数据包括故障线路单位长度的串联阻抗矩阵和并联导纳矩阵、随故障变化而不断变化的电力系统正序阻抗矩阵Zbus和故障类型。基于所涉及的计算量和性质，建议使用存储在故障记录器或数字保护继电器中的电流和电压数据进行离线计算。结果表明，该方法能够对各类故障进行高精度的故障距离估计，但是故障电阻大小须在实际中常见的故障电阻值的正常范围内。然而，当单相接地故障和两相相间故障的故障电阻值为偏离实际的较高值时，观测数据存在较大的误差。该方法对局部母线阻抗值的误差特别敏感，但对远端母线阻抗值的误差不敏感。