顺层水力导向压裂增透技术在低透气性松软煤层的应用研究

赵伟伟

(山西西山晋兴能源有限责任公司 斜沟煤矿，山西 吕梁 033602)

低渗透高瓦斯松软煤层瓦斯抽采难度较大，采用现行瓦斯抽采工艺较难完成本煤层瓦斯抽采达标，特别是单一煤层开采时，为了保证采掘安全必须采取增透措施[1-3]。目前，针对煤矿井下水力增透技术已有相关研究，周西华等[4]分析了煤层钻孔间距对水力压裂增透效果的影响；何福胜等[5]研究了穿层钻孔水力压裂增透效果及压裂参数优化；边小峰等[6]在高瓦斯煤层进行了水力压裂增透的对比实验研究；刘军[7]系统研究了水力压裂钻孔封孔的力学模型并进行了现场试验；吴拥政等[8]在潘北矿井下进行了水力压裂增透试验研究；石欣雨等[9]在复杂地质条件下开展了割缝与压裂协调的增透实验；许江等[10]在实验室完成了真三轴作用下水压压裂对煤岩层作用的物理模拟实验。煤层水力压裂增透技术具有较好的应用前景，为了提升煤层水力压裂的增透效果，本文提出在低渗透高瓦斯松软煤层开展高压水力割缝形成导向槽后的水力压裂增透方法，并结合斜沟煤矿煤层瓦斯赋存条件运用该方法进行增透机理的相关研究[11]。

1 煤层水力导向压裂增透机理分析

低渗透高瓦斯松软煤层井下顺层水力导向压裂增透技术是利用高压水射流割缝设备首先对原始煤体钻孔内进行割缝形成较大的裂缝，这些大尺度的裂纹为水力压裂提供了导向的作用；随后利用高压水作为动力，注入钻孔内的高压水克服煤层自然滤失和应力的作用，大量的水注入原始煤体的孔洞及裂隙中，持续压裂促使煤体形成新的裂隙及导通裂隙网络，从而增加煤层的渗透性，最终提高本煤层瓦斯抽采率[12-13]。

煤层水力压裂过程中，空间地应力决定裂隙扩展延伸的路径和形态。假设在不考虑煤体滤失作用条件下，目标煤体各项均质且裂隙沿压裂钻孔对称延伸[14]，则简化后的煤体内裂隙形态如图1所示。

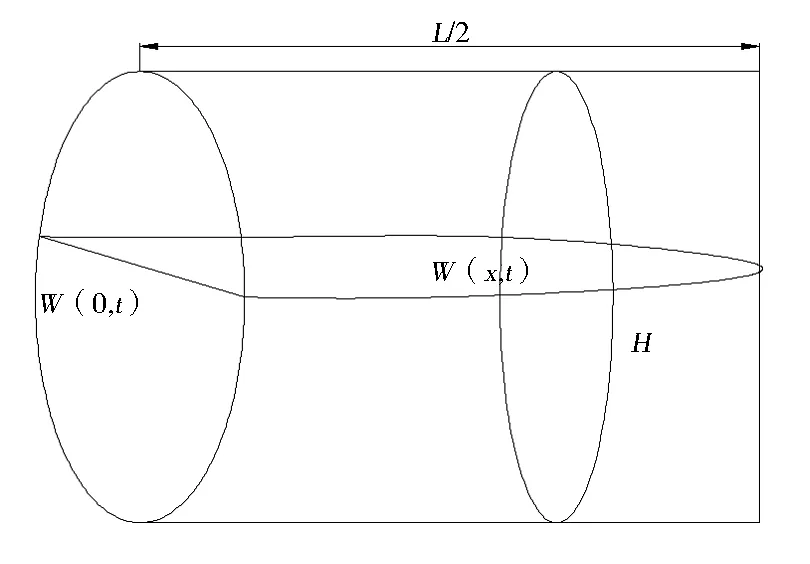
图1 裂隙延伸形态简图

由England提出在平面应变条件下的裂隙内壁表面上任意正应力p与裂隙宽度W的关系为：

(1)

式中：fL=x/L，且f1、f2为裂缝长度系数(-L≤x≤L)；G为剪切模量，MPa；v为泊松比；E为弹性模量，MPa。

依据断裂力学和流体力学理论得出裂隙体积:

式中：H为煤层厚度，m；Q为裂缝延伸平均瞬时排量，m3/min；t为时间，min。

压裂钻孔对称裂隙全长：

(3)

式中：μ为液体动力粘度，Pa·s。

压裂钻孔单条裂隙长度：

(4)

将式(4)代入式(2)可以得到水力压裂钻孔裂隙宽度方程：

(5)

水力压裂提高煤层渗透率的模型可以定义为：煤层在水力压裂过程中，压裂钻孔长度与压裂新生裂隙数量成正比，压裂钻孔范围内有a条原生裂隙扩展延伸，则单条裂隙承受泵注入压裂液的体积为：

(6)

式中：Qn为单条裂隙注液体积，m3；Q为压裂泵注液总体积，m3；l为压裂钻孔长度，m。

将式(6)代入式(4)和(5)，可以得到距离压裂钻孔任意位置单条裂缝内注入的压裂液体积，则注入的压裂液体积表征为裂隙大小，从而间接推导出孔隙度方程：

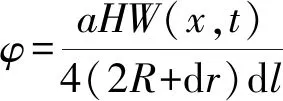
(7)

式中：R为距离压裂钻孔的距离，m。

由Carman-Kozeng方程：

(8)

式中：T为压裂钻孔裂隙曲折系数。

将式(7)代入(8)可以推导得出距离压裂钻孔R处的渗透率方程为：

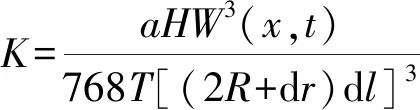
(9)

由式(9)可知，距离水力压裂钻孔R处的渗透率随距离的增大减小；在相同煤层厚度和原生裂隙条件下，渗透率与压裂时间具有正线性关系。

2 煤层水力导向压裂数值模拟分析

由于煤层属于非匀质的固体，使得采用煤层的本构关系不能解释煤层压裂过程中破坏机制，通过分析煤层微观结构研究压裂增透机理，已有研究表明，煤层受到外力作用后其内部结构被破坏是造成煤层力学性质变化的主要原因。煤层损伤破裂过程渗流-应力耦合数值模拟软件RFPA2D-Flow对研究煤岩体裂隙发育与扩展中渗透率演化和流固耦合机理具有良好的适用性和准确度。

2.1 数学模型

RFPA2D-Flow对煤层多孔介质流固耦合的数学模型主要由变形场、渗流场、渗流与变形耦合模型等组成，各数学模型如下：

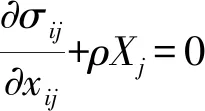
(10)

本构方程：σ'ij=σij-αPδij=λδijεv+2Gεij

(11)

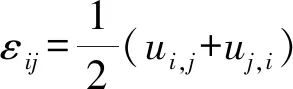
(12)

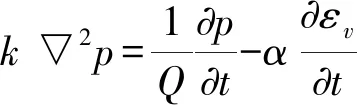
(13)

渗流-应力耦合方程：k(σ，p)=

(14)

式中：Q为Biot常数；ρ为体积密度；εv，εij分别为体应变和正应变；δ为Kronecker常数；G为剪切模量；λ为拉梅系数；▽2为拉普拉斯算子；k为渗透系数；k0为原始渗透系数；P为孔隙水压力；α为实验确定的孔隙水压系数；β为实验确定的应力敏感因子。

2.2 物理模型

以斜沟煤矿的8号煤层为研究对象，模拟回采工作面为18205大采高工作面，煤层平均厚度为4.81 m，煤层倾角为3°左右的近水平煤层，回采区域埋深为500 m左右，本煤层钻孔孔径为113 mm，模型使用的物理参数如表1所示。本次数值模拟建立的模型尺寸为200 m×200 m的二维平面模型，模型如图2所示。

图2 8号煤层水力压裂模型

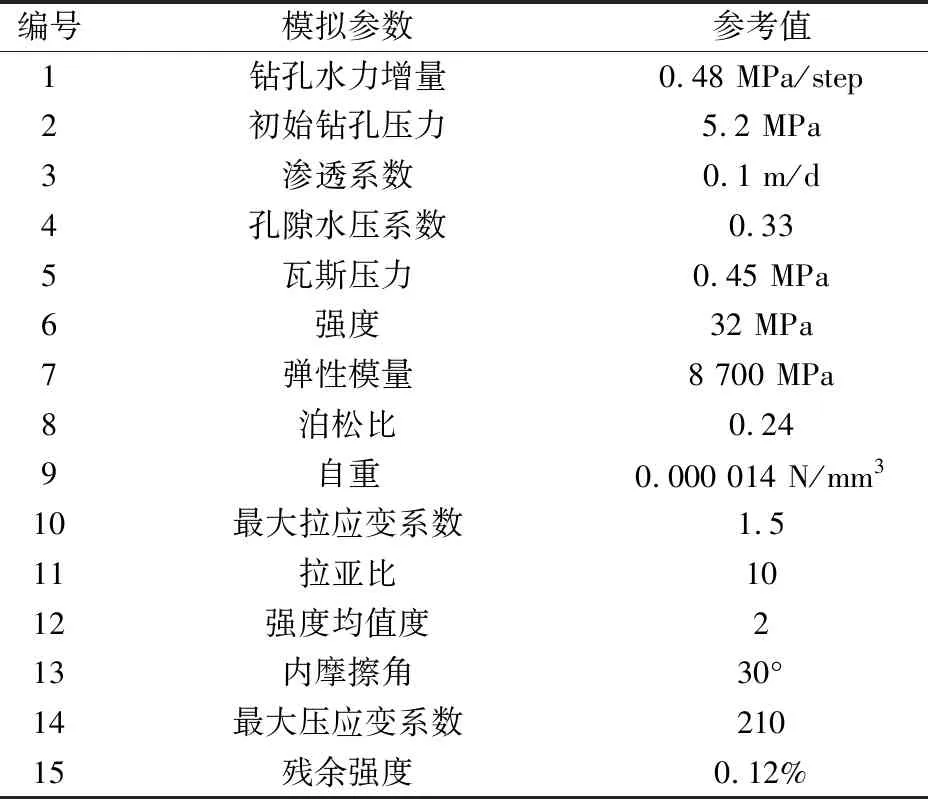
表1 8号煤层高压水射流导向压裂增透数值模拟参数

2.3 数值模拟结果分析

为了研究斜沟煤矿8号煤层12采区18205工作面本煤层水力导向压裂增透效果，本次采用基础物理参数一致的情况下，模拟实验一为本煤层顺层钻孔未采取任何措施时运用水力压裂过程中煤体的演化特征，模拟实验二为本煤层顺层钻孔先采用高压水力割缝后，再进行水力压裂过程。模拟过程中选取0 MPa、5 MPa、10 MPa、15 MPa、20 MPa、25 MPa、30 MPa、35 MPa和40 MPa共9个升压时刻的压裂钻孔周围煤体演化特征，模拟实验一水力压裂过程演化如图3所示，模拟实验二水力压裂过程演化如图4所示。

图3 煤层常规钻孔(D113 mm)水力压裂过程演化

图4 煤层常规钻孔采用水力割缝导向深度(D200 mm)

由图3可以看出，水力压裂形成的新生裂隙以钻孔为轴线对称分布，最终裂隙网络成“沙漏”形状。从图3(a)～(e)可以看出压力值从0 MPa逐渐升至20 MPa过程中，煤体未开始起裂，此时压力强度未达到煤体所受应力强度，当压力值达到25 MPa时，沿近水平方向上形成了明显的裂隙，随着压力增大，沿着该裂隙逐渐向水平方向延伸并向纵向扩展，最终形成半径为3 m左右的水力压裂裂隙网络。

图4为本煤层常规钻孔在采用高压水力割缝形成最大直径为200 mm导向槽后，再进行水力压裂过程演化，由图4(d)可以看出在压力值升至15 MPa时，压力钻孔开始起裂，当压力值升至30 MPa时，裂隙扩展半径达到了3 m左右，随着压力值持续升至40 MPa时裂隙扩展半径达到了6 m，最终裂隙网络形成“喇叭花”形状。

3 现场试验

为了考察顺层水力导向压裂的增透效果，在18205工作面材料巷开展试验。在材料巷625 m处试验本煤层顺层钻孔未采取任何措施时运用水力压裂技术，在材料巷825 m处试验本煤层顺层钻孔先采用高压水力割缝后，再进行水力压裂技术。试验区域钻孔布置如图5所示，钻孔直径113 mm，开孔高度1.5 m，倾角为-7°，方位角为270°，钻孔长度为60 m，材料巷825 m处1号检验孔与2号割缝孔间距为3 m，2号割缝孔与3号检验孔间距为6 m；材料巷625 m处4号检验孔与5号未割缝孔间距为3 m，5号未割缝孔与6号检验孔间距为3 m。连续观测试验前后压裂孔周围抽采孔内的瓦斯浓度和流量，得到相关数据后，运用数据缝隙软件进行对比分析。

图5 钻孔布置示意

1) 水力割缝前后瓦斯抽采量对比如图6所示。由图6可知，采取水力割缝后瓦斯抽采量显著升高，水力割缝前瓦斯抽采量为15.9～21.8 m3/d，水力割缝后瓦斯抽采量为34.8～53.7 m3/d，是水力割缝前的2.18～2.46倍，平均抽采量比割缝前增大了1.29倍。在水力割缝后前7 d内抽采量升高速度较快，之后伴随着时间的推移瓦斯抽采量逐渐衰减，但仍然超过水力割缝前的抽采量，预抽时间也明显缩短。

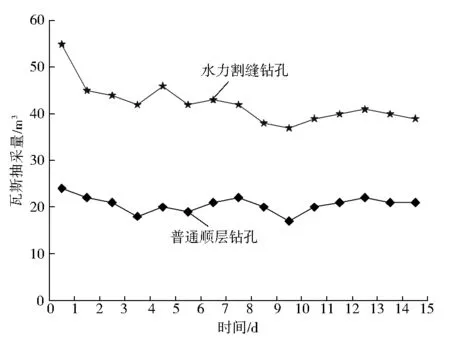
图6 水力割缝前后瓦斯抽采量

2) 水力割缝前后的煤层透气性系数对比如图7所示。由图7可知，未采取水力割缝技术时的钻孔抽采时，煤层透气性系数为0.025 137 m2/(MPa2·d)，采取水力割缝后煤层透气性系数为0.141 925 m2/(MPa2·d)，比未采取水力割缝技术增大了4.65倍。采取水力割缝技术后在前10 d内煤层透气性系数变化幅度最大，证明水力割缝产生的裂隙发生闭合现象，30 d后煤层透气系数大小基本保持稳定，90 d后煤层透气性系数还是高于原始煤层透气性系数2.29倍。

综上分析得到，煤体在采取水力割缝的水力压裂增透技术后，原生裂隙发生扩展的同时，还生成了大量的新裂隙。在水力割缝初期，煤层透气性增加的速度很快，在地应力作用下裂隙随着时间的推移发生闭合的现象，但因为控制孔的作用，形成了不可恢复的裂缝裂隙，在后续的试验中可尝试用其他介质开展辅助割缝，进而充分利用割缝初期形成的裂隙或者降低裂隙裂缝的闭合程度。

图7 水力割缝前后煤层透气性系数变化

4 结 语

1) 分析了煤层水力导向压裂增透机理，推导得出了距离水力压裂钻孔R处的煤体渗透率方程为꿱研究得出距离水力压裂钻孔R处的渗透率随距离的增大而减小；在相同煤层厚度和原生裂隙条件下，渗透率与压裂时间具有正线性关系。

2) 以斜沟煤矿18205工作面为对象，开展本煤层钻孔是否采取水力割缝的水力压裂增透数值模拟研究，得出常规顺层钻孔水力压裂增透半径为3 m，而运用水力割缝后进行导向水力压裂增透半径达到了6 m。

3) 现场试验表明，水力导向压裂增透技术能够有效改造低渗透高瓦斯松软煤层煤体裂隙结构，有效提升煤层的渗透性，从而提高本煤层瓦斯抽采的效果。