智能网联环境下基于混合深度学习的交通流预测模型

陆文琦，芮一康，冉 斌*，谷远利

(1.东南大学a.交通学院，b.东南大学—威斯康星大学智能网联交通联合研究院，c.城市智能交通江苏省重点实验室，南京211189；2.北京交通大学综合交通运输大数据应用技术行业重点实验室，北京100044)

0 引 言

人工智能、大数据及5G 通信技术日渐成熟，车路协同自动驾驶(Connected and Automated Vehicle Highway，CAVH)已逐渐成为智能交通系统的终极发展形式，是缓解交通拥堵，提高交通安全和减少排放的重要技术[1].作为CAVH 的关键模块之一，精细化短时交通流预测既是网联车(Connected Automated Vehicle,CAV)路径决策规划的基础，也是混合交通流环境下实现群体优化与协同控制的重要保障.

交通流预测技术已经从基于统计学的参数方法[2]和机器学习驱动的非参数方法[3]逐渐演化为大数据驱动的深度学习方法.Pamuła[4]基于图像处理技术利用卷积神经网络和多层感知机识别并预测交通状态；MA 等[5]将长短期记忆神经网络(Long Short-Term Memory，LSTM)引入交通领域，实现交通流速度的时间序列预测；王祥雪等[6]对交通流进行时间序列重构和标准化处理，在此基础上，利用多层LSTM 网络构建多时间梯度交通流预测模型；谷远利等[7]利用基于信息熵的灰色关联分析提取交通流空间特征，并采用双层循环神经网络(Recurrent Neural Network，RNN)实现快速路车道级速度预测.

现阶段交通流预测主要基于原始速度或流量数据，未考虑将原始数据分解为规律性更强的时间序列分量，从而优化模型输入.此外，现有研究主要针对非网联场景，对智能网联环境下交通流预测的研究较少.在CAVH 环境下，车道交通流的速度、流量等参数可依靠CAV 实时采集，并通过车—路通信模块与路侧单元(Road-Side Unit,RSU)实时交互，RSU 将交通流信息传输至交通控制中心(Traffic Control Center，TCC)实时处理，借助TCC 强大的数据计算能力，原始车道级交通流数据可被实时分解为规律的时间序列分量，并将时间序列分量重构为TCC 中深度学习模型输入，有效提升预测精度.

因此，本文提出一种面向CAVH 系统的混合深度学习(HDL)交通流速度预测模型.利用集成经验模态分解 (Ensemble Empirical Mode Decomposition,EEMD)[8]处理原始车道级交通流速度数据并重构为深度学习模型输入，引入注意力(Attention)机制和双向LSTM 构建预测模型框架.实测交通流数据验证表明，该模型具有良好的预测精度和适用性，且模型构建机理符合CAVH 技术发展需求.

1 集成经验模态分解

集成经验模态分解(EEMD)[8]是在经验模态分解(Empirical Mode Decomposition, EMD)[9]基础上提出的信号分解方法.EMD 是一种处理非平稳非线性序列的时空分析方法，可将原始时间序列，如交通流速度序列V(t)分解为M个固有模态函数(Intrinsic Mode Function, IMF)分量Vm(t)和残差序列R(t)，即

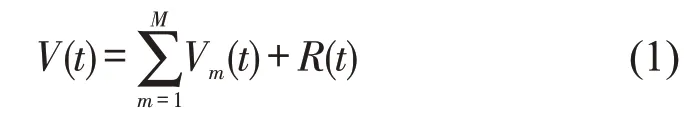
式中：Vm(t)为序列V(t)的第m个IMF 分量，m=1,2,…,M；M为IMF分量数目；t为序列的时间刻度.

通常IMF 分量必须满足两个约束条件：①在整个时间序列上，IMF分量的极值点和过零点的个数必须相等或相差不超过一个；②任意时刻，IMF分量的局部上、下包络线均值为0.EMD 算法分解步骤如下.

Step 1识别原始速度序列V(t)的所有局部极大值和极小值点，并利用曲线拟合构造出所有上、下包络线，得到均值曲线M1(t)和新的分量H1(t).

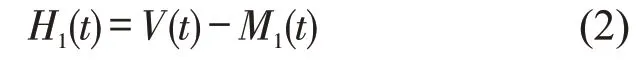
Step 2判断.若H1(t)满足IMF 的两个条件，设H1(t)为V1(t)；否则，设H1(t)为V(t)，并返回Step 1.

Step 3计算R(t).

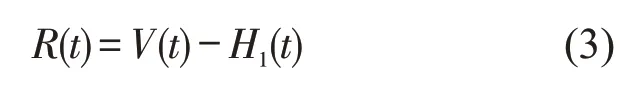
Step 4设R(t)为V(t)，重复Step 1～Step 3找到所有IMF分量，直到R(t)成为单调的残差函数.

然而，由于分解过程中信号极值点分布不均衡，EMD 存在模态混叠现象，因此，Wu 等[8]提出EEMD 模型，在原始序列中加入相同幅值的白噪声，改变序列中极值点分布，消除模态混叠效应.多次平均后，白噪声将相互抵消，集成均值结果作为最终分解结果.综上，EEMD分解过程如下.

Step 1初始化迭代次数S和白噪声的标准差ε.

Step 2将白噪声Ns(t) 加入原始速度序列V(t)，生成添加过噪声的速度序列V(s)(t)为

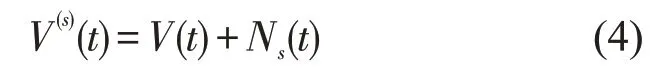
Step 3对S个含噪声的序列进行EMD分解，获得S个IMF分量和S个残差分量R(s)(t)，其中，为第s次分解的第m个IMF 分量，m=1,2,…,M，R(s)(t)为第s次分解的残差分量.

Step 4计算出第m个IMF 分量的均值和残差的均值.

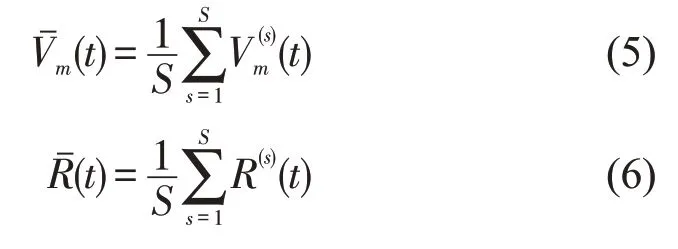
2 双向长短期记忆神经网络

长短期记忆神经网络(LSTM)[10]是现阶段最为流行、认可度最高的循环神经网络，能够克服RNN存在的梯度消失问题，已成为解决时间序列预测问题的经典方法.在交通流预测领域，LSTM 被广泛应用于捕获交通流的时间特征.

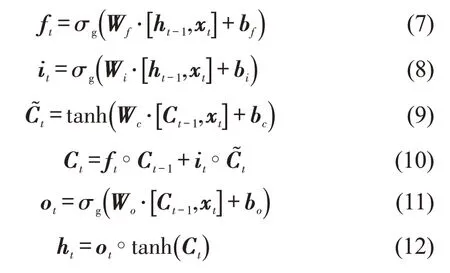
式中：σg为sigmoid 激活函数；∘为两个向量的乘积；xt为输入向量；为候选细胞信息向量；ht为隐藏层输出向量；Wf,Wi,Wo,Wc,bf,bi,bo和bc为需要训练得到的权值和偏移量.

双向LSTM(BiLSTM)结合双向RNN和LSTM的优点，如图2所示，BiLSTM由一个前向LSTM隐藏层和一个后向LSTM 隐藏层组成，且这两个隐藏层都连接着一个输出层，同时为输出层提供前向和后向的信息.BiLSTM的输出为

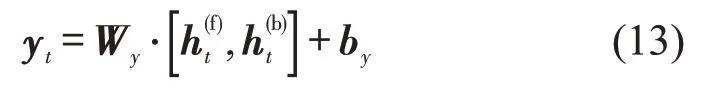
式中：和分别为前后向隐藏层的输出；Wy和by为权重和偏置.

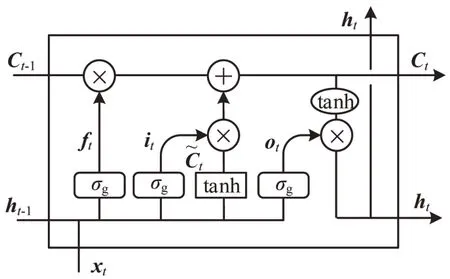
图1 经典LSTM 记忆模块Fig.1 Memory block of classical LSTM

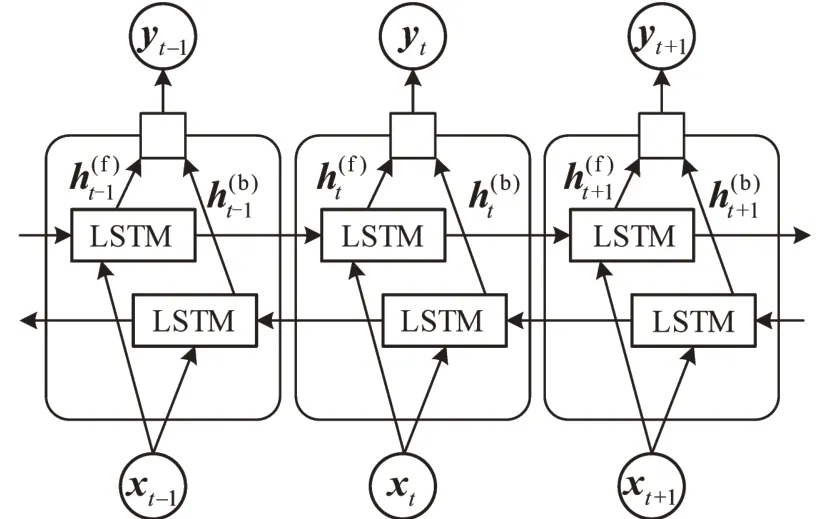
图2 BiLSTM 神经网络结构Fig.2 Structure of BiLSTM neural network

3 CAVH环境下基于混合深度学习的车道级速度预测模型

3.1 模型结构

在CAVH 环境下，短时交通流预测的研究对象为车道断面的交通流运行状态，而车道级交通流具有较强的时变性和非线性特征.为实现CAVH环境下车道级速度的短时高精度预测，本文提出集成EEMD、BiLSTM和Attention机制的混合深度学习模型(Hybrid Deep Learning model,HDL).

如图3所示，HDL模型基于CAVH系统强大的数据传输和并行计算能力，在TCC 中利用EEMD算法将车道交通流速度序列分解为若干IMF分量及残差分量，并依据输入步长重构模型输入.同时，依靠TCC 训练和存储深度学习框架，利用BiLSTM挖掘重构输入的时间特征，引入Attention机制对BiLSTM 隐藏层输出的特征向量赋予不同的权重，加强重要信息提取.最后，通过全连接层将特征向量转换为预测结果输出.

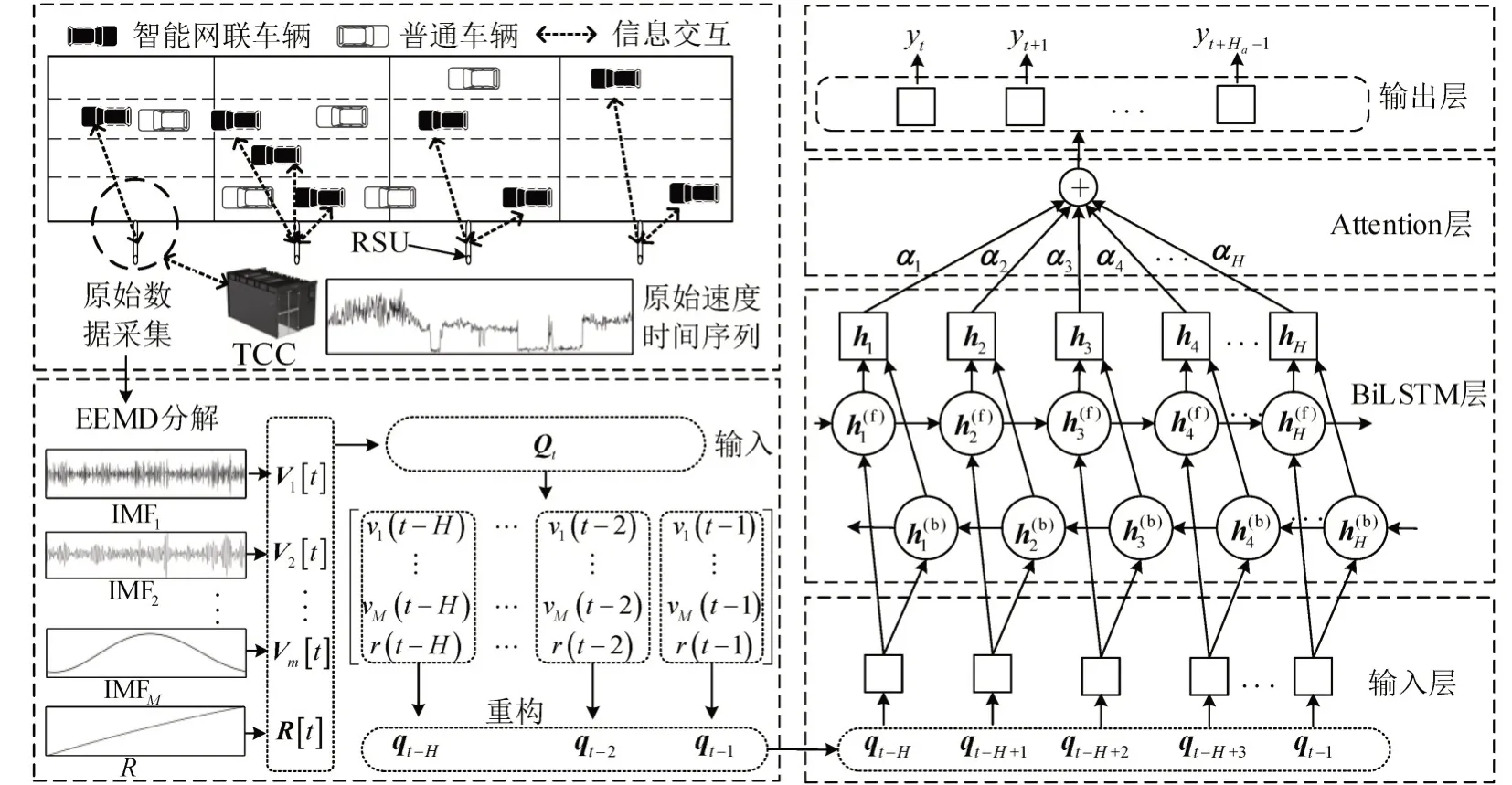
图3 混合深度学习模型结构示意图Fig.3 Structure of HDL model

模型各层的具体描述如下.

(1)输入层.利用RSU实时获取CAV发送的位置、速度等信息，通过TCC 预处理，获取目标车道断面时间步长为H的原始速度序列V[t] ，V[t] =[v(t-H),…,v(t-2),v(t-1) ]，其中，v(t)为t时刻目标车道断面的速度.基于EEMD算法可将V[t]分解为M个IMF 序列Vm[t],m=1,2,…,M和一个残差序列R[t] ，其中，Vm[t] =[vm(t-H),…,vm(t-2),vm(t-1) ]，R[t] =[r(t-H),…,r(t-2),r(t-1) ]，t时刻HDL模型输入为

7.1.3 应根据《中华人民共和国食品安全法》第五十三条的规定，收集和索取所有供应商的合法证件，以及产品合格证明文件，并及时更新过期的证件与文件。

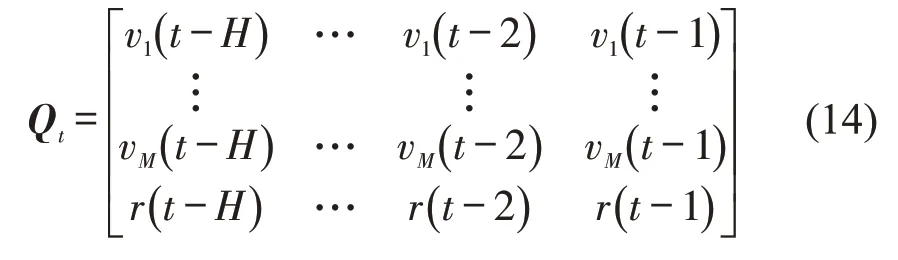
(2)BiLSTM 层.对输入的重构序列变量Qt的时间特征进行提取，双向结构可以更好地保证模型对长期特征的记忆，BiLSTM在t时刻的输出为

(3)Attention 层.通过概率分配的方式对关键信息分配足够的权重，从而更全面地获得重构向量特征，突出重要信息的影响，提高预测模型的准确率. 该层输入为BiLSTM 层的输出矩阵Ht=[h1,h2,…,hH]T，Attention 层在t时刻的权重系数αt和输出pt为

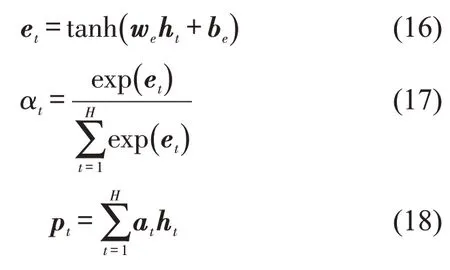
式中：et表示t时刻由BiLSTM层输出向量ht所决定的注意力概率分布值；we和be为权重和偏置.

(4)输出层.将Attention 层输出通过全连接计算出预测步长为Ha的预测结果yt=[yt,yt+1,…,yt+Ha-1]T，其中，yt为

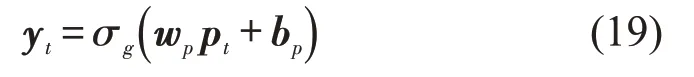
式中：wp和bp为权重和偏置.

3.2 损失函数

HDL 模型以均方误差函数为优化目标，目标函数为

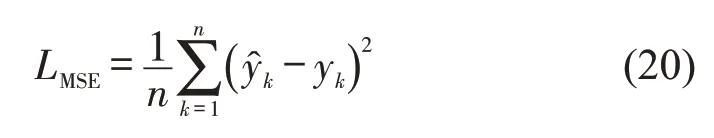
式中：LMSE为均方误差(MSE)函数；n为训练样本数量k为预测值；yk为观测值.

训练过程中，选择Adam算法更新模型的权值和阈值，与传统随机梯度下降算法不同，Adam 通过计算一阶矩估计和二阶矩估计为不同的参数设计独立的自适应性学习率，从而更新参数并使损失函数输出值达到最优.

4 实验分析

4.1 实验数据与评价指标

受实验条件限制，无法构建真实的CAVH 环境采集宏观交通流数据，采用北京市二环快速路外环车道级交通流速度数据检验混合深度学习模型的精度和可靠性.速度数据由路侧微波检测器采集，为车道断面以2 min 为间隔的平均车速，将此数据集类比为图3中CAVH 环境下RSU 与CAV数据交互和处理后得到的车道级速度序列数据.如图4所示，数据采集范围包括5条道路的15个车道断面，采集时间为2014年1月6日～2月2日的全天时段，即单车道采集的速度序列样本为720个/天，以前21天数据为训练集，后7天数据为测试集.

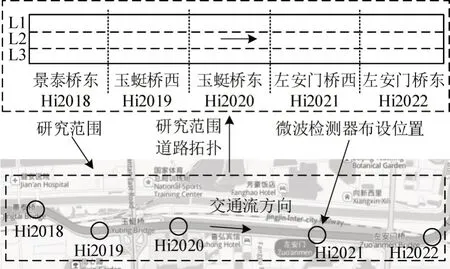
图4 研究范围和检测器布设示意图Fig.4 Schematic diagram of research scope and detector layout

为评估模型的预测性能，选择平均绝对误差(MAE)和平均绝对百分比误差(MAPE)评价模型精度，利用希尔不等系数(TIC)评价模型的拟合度.TIC值越小，拟合程度越高.

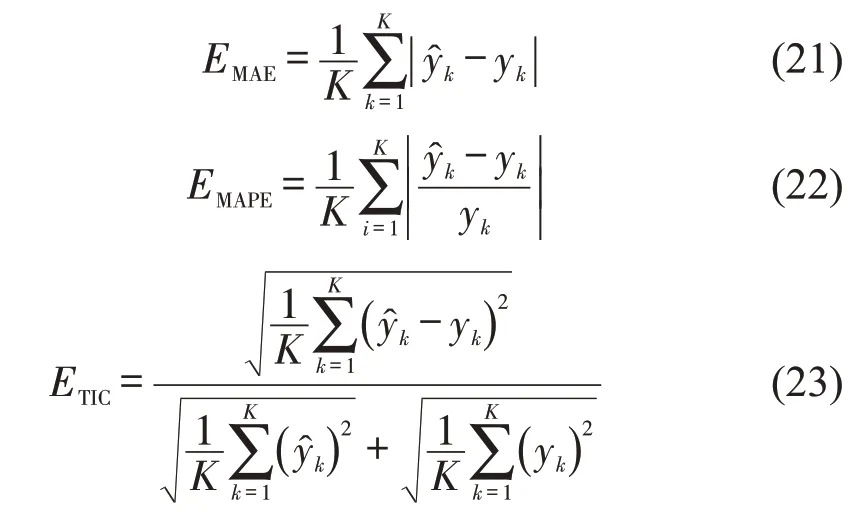
式中：为速度预测值；yk为速度实测值；K为预测样本数量.

4.2 模型实施

实验环境为DELL 计算机(Inter(R) Core(TM)i7-8700CPU，8 G RAM)，以Tensorflow 中Keras 高层神经网络API 为框架，在Python3.6 环境中完成模型搭建和训练.其中，HDL模型的超参数设置如下：训练迭代次数为100 次，批大小为64，BiLSTM隐藏层神经元个数设置为128，为减小过拟合，BiLSTM和全连接层间设置Dropout，随机断开20%的神经元.EEMD分解过程中噪声标准差为0.2，生成的噪声序列个数为500，最大迭代次数为50.

4.3 结果分析

(1)不同模型预测结果对比.

选择ARIMA、多层感知机(MLP)、径向基函数神经网络(RBFNN)、LSTM、门控循环单元网络(GRU)、BiLSTM 和EMD-BiLSTM 与本文模型对比，检验模型精度和可靠性.ARIMA采用赤池信息量准则选择参数组合；MLP和RBFNN均为3层结构，隐藏层神经元个数为200，考虑上下游对预测车道的影响，输入时间步长为10，即对单车道而言，输入变量个数为90，其中，RBFNN采用高斯核函数作为径向基函数；LSTM、GRU、BiLSTM 和EMD-BiLSTM模型的超参数设置如4.2节所述，输入模型的时间步长为10，均采用Adam算法进行训练，其中，BiLSTM 算法中包含Attention 机制，EMD- BiLSTM 采用EMD 分解重构输入和Attention机制的双向LSTM算法.表1为不同方法单步预测的总体结果，图5为各算法在不同车道的预测效果.

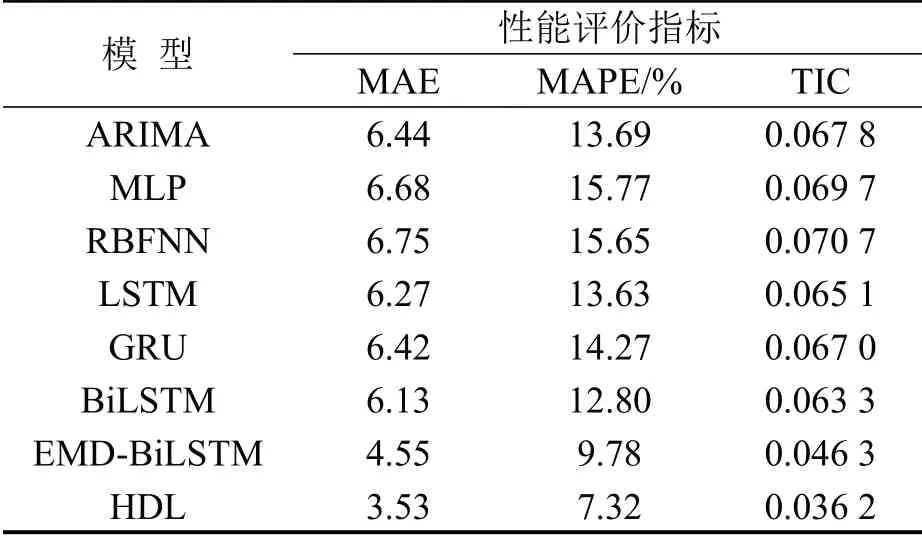
表1 不同模型总体预测结果Table 1 Overall prediction results of different models

从表1可知：ARIMA、LSTM和GRU模型的各指标较为接近，表明针对车道级速度预测而言，单一模型的预测效果区别较小，且考虑时空特征的机器学习模型(MLP、RBFNN)与仅考虑时间特征的深度学习模型(LSTM、GRU)相比无显著优势；BiLSTM 考虑双向特征和Attention 机制，与LSTM模型相比，MAE 和MAPE 分别优化了2.23%和6.09%；EMD-BiLSTM 利用EMD 分解方法对时间序列输入进行分解重构，与BiLSTM 相比，MAE、MAPE 和TIC分别提升了25.77%、23.59%和26.86%；本文HDL模型利用EEMD算法取代EMD算法，进一步提升了预测效果，与EMD-BiLSTM相比，MAE 和MAPE 分别优化了22.42%和25.15%.实验结果表明，采用EEMD算法可有效优化模型输入，提升混合模型的预测精度.

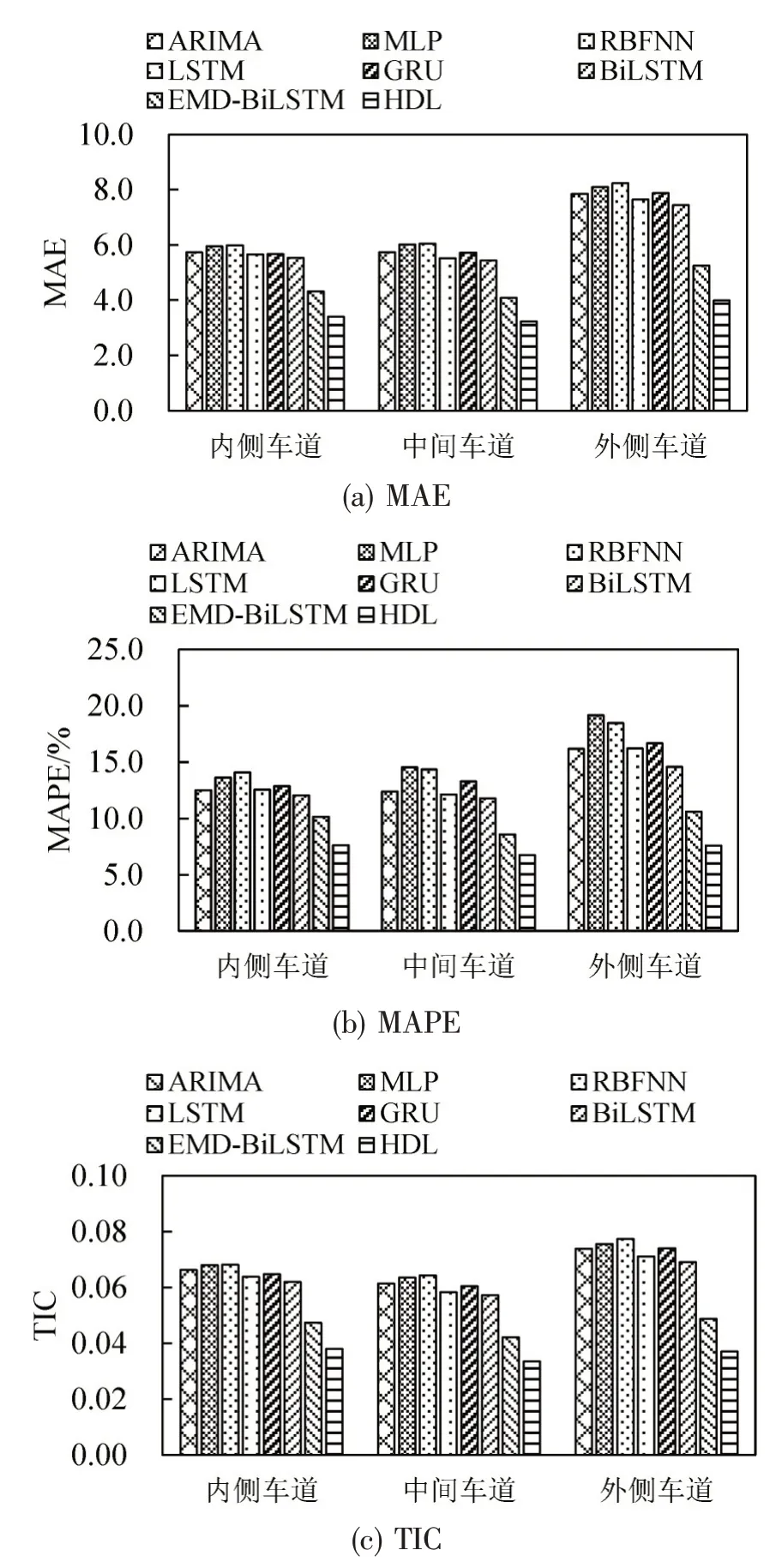
图5 各算法在不同车道预测结果Fig.5 Prediction results of different models at different lanes

由图5可知：各算法在内侧和中间车道预测效果最佳，这主要是由于外侧车道受超车行为和车辆汇入影响，车速波动较大，增加了预测难度.本文HDL 模型预测效果最好，在车速较为稳定的中间车道，MAE 和MAPE 达到3.22 和6.76%，与EMD-BiLSTM 相比两项指标分别提升21.04%和21.30%.

(2)参数分析.

分析输入步长、IMF 分量数目及预测步长对HDL 模型性能的影响.图6 为不同输入步长下预测精度和模型训练时间的变化情况.由图6 可知，随输入步长的增加，HDL 模型预测精度先显著提升后逐渐稳定，单个目标车道预测的训练时间显著增加.考虑模型精度和训练时间，HDL模型理想输入步长为10～15.

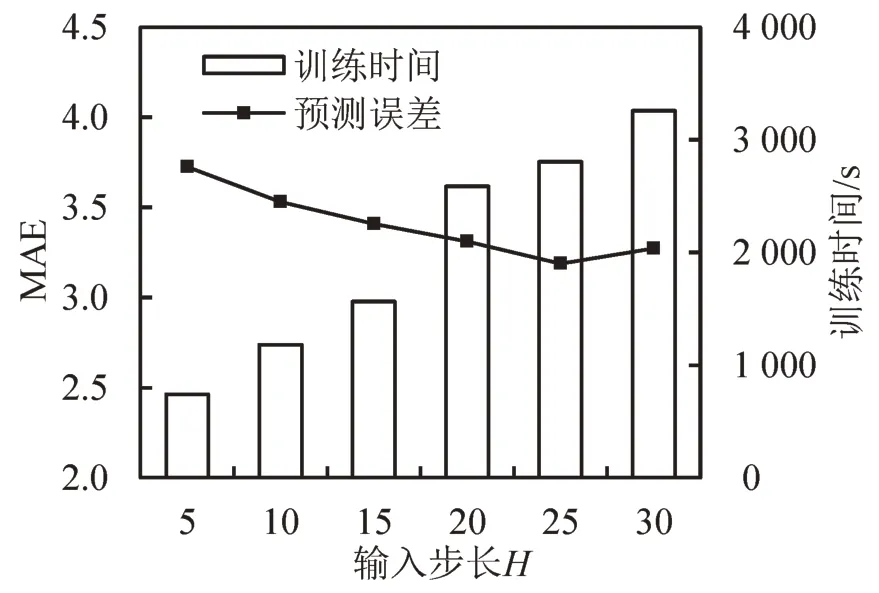
图6 输入步长与模型精度和训练时间关系Fig.6 Relationships among input time step,accuracy,and training time in HDL model

输入步长为10 时，IMF 分量数目对模型精度的影响如图7 所示，分别考虑前5 个，前10 个，以及全部(＞10)IMF 分量作为模型输入.由图7 可知：IMF 分量数目较少时，无法包含足够有效的交通流信息，EMD-BiLSTM和HDL模型的预测精度偏低；IMF 数目大于10 时，两者均可获得较为理想的预测精度，且HDL 的预测误差小于EMDBiLSTM.

图8为不同预测模型多步预测结果，预测步长由1 逐步增长到5.结果表明，随着预测步长的增加，各模型的MAE 逐渐增大，EMD-BiLSTM 和HDL 模型精度始终高于其他模型，说明原始速度序列经过EMD 和EEMD 分解重构后的深度学习模型具有良好的预测精度和稳定性.

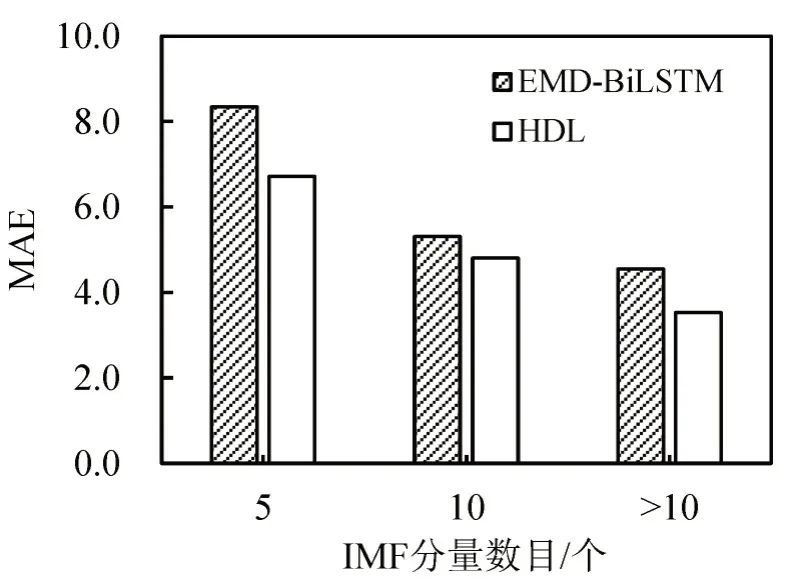
图7 IMF 分量数目与模型精度的关系Fig.7 Relationship between input number of IMFs and accuracy in HDL model

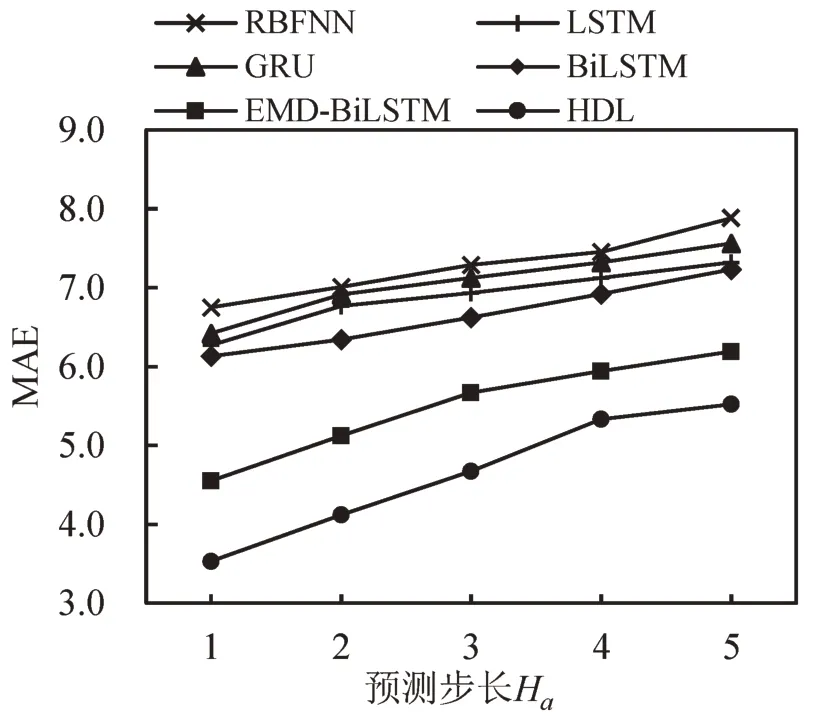
图8 不同模型多步预测结果Fig.8 Different models in task of making multi-step-ahead prediction

5 结 论

针对智能网联环境对交通流预测实时性和精细化的需求，本文提出适用于CAVH 环境的混合深度学习交通流预测模型.模型采用集成经验模态分解(EEMD)结合CAVH 下交通流可实时分解重构特性，将原始输入速度序列分解为多个经验模态分量并重构为输入矩阵，利用双向LSTM 和注意力机制构建深度学习网络框架提取重构输入的时间特征，实现CAVH 环境下的车道级短时交通流速度预测.现阶段构建完整的CAVH 环境存在困难，故采集北京市二环快速路的交通流速度参数检验模型的精度和可靠性.实验结果表明，在单步预测过程中，HDL模型的MAE、MAPE和TIC显著优于其他模型，随着预测步长的增加，HDL的精度无显著下降，因此，该模型的构建机理和预测效果均能满足CAVH技术发展的需要.