藤Copula 模型在我国股市多资产组合 VaR 预测中的应用
徐刚刚,蔡学鹏,熊尚敏
(新疆农业大学数理学院,新疆,乌鲁木齐 830052)
0 引言
在大数据时代繁荣发展的今天,金融序列数据不仅表现出传统的“高峰厚尾”、集聚性以及非对称性等特点,还具有动态的时变性、时速快和维数高等大数据特点,因此对金融数据理论方法的研究亟待创新。Copula 作为一种连接函数,在度量多变量之间的相关结构方面得到了许多读者的青睐,尤其在金融风险管理领域。其中Embrechts 等[1]对此做出了重要的贡献,首次应用Copula 函数研究金融数据,随后国内外大量学者利用Copula 函数在金融资产定价、金融市场相关性等方面做出了有意义的成果。例如我国学者吴振翔等[2]将Arichimedean Copula 和VaR 理论结合在一起,运用于研究外汇投资组合问题;柏满迎等[3]利用三种Copula 与VaR理论将美元和欧元进行组合研究它们之间的相依结构和预测风险价值;Patton[4]利用动态Copula 模型建模,分析了国际外汇市场动态相关性等问题。然而以上文献对高维变量问题并未做过多讨论,如果只停留在二维Copula 模型的研究上,对分析实际中的多资产变量问题来说意义不大,因此对Copula理论在高维的拓展问题上展开讨论显得很有必要。
藤Copula 模型作为一个新的理论创新方法为人们所接纳,它是在Joe[5]提出的Pair Copula 模型的基础上进行构建的,其原理是利用Pair Copula 模型将变量之间的二元Copula 函数组建到一起,从而形成具有藤结构的Copula 模型组。由于每个Pair Copula 可以根据具体变量间的相依结构而选择合理的Copula 函数,具有较强的灵活性,因此用Vine-Copula 模型刻画多资产金融序列就显得较为合理。在实际问题的研究中,Bedford 等[6]对此技术进一步深入分析,提出了Regular Vine(R-Vine)结构,并衍生出两种特殊的藤结构,分别为Canonical Vine(C-Vine)和Drawable Vine(D-Vine);Yew Low等[7]认为在管理多资产组合应用上C-Vine 更合理;我国学者谢赤[8]利用几类藤Copula 探讨了金砖国家股指期货市场的相关结构及谱风险度量,得出了在C-Vine 结构下,南非市场在金砖市场中的重要性。由于金融序列均存在“高峰厚尾”和非对称等特点,而这些特点都会严重影响最终的VaR 预测。因此应用不同特点的Pair Copula 来分析金融序列的局部特点同样显得很有意义。
鉴于此,本文研究的主要问题有以下几点:第一,在边缘分布的选取上,由于考虑到金融数据的“高峰厚尾”性、动态时变性以及非对称性等特点,本文选择ARMA(1,1)-GJR(1,1)-SkT 模型来刻画各序列;并探讨了藤Copula 密度函数的推导过程以及藤结构中Pair Copula 的排序与选择、节点等问题;第二,为了体现藤Copula 模型的灵活性与实用性,先将R 藤中的Pair Copula 函数固定为t-Copula 和Gumbel Copula,即R-Vine all t 模型和R-Vine all Gumbel 模型,再与R-Vine 模型的检验结果进行比较;另外,将R-Vine all t 模型和R-Vine all Gumbel模型做比较,从而可以反映出R-Vine all Gumbel 模型在拟合具有非对称和厚尾特点的金融序列上更占优势;第三,因为序列具有时变性,因此在Vine Copula 模型的参数估计时应用了滚动Monte Carlo模拟的思想,在动态VaR 计算时利用滚动时间窗口方法进行预测;其次在模型VaR 预测效果稳健性检验过程中利用Mean-CVaR 约束条件[9~12]重新确定权重,这样做更符合实际;第四,在模型检验中采用常用的AIC 和BIC 信息准则,在VaR 预测结果中利用成熟的Kupiec 返回值检验法验证几种藤Copula 的预测效果,在理论依据上具有一定的可靠性。
1 边缘分布模型
股票收益率数据一般具有“高峰厚尾”及非对称等特点[13],在GARCH 族模型中,通常假定标准化残差序列服从正态分布、t 分布以及GED 等分布,而这些分布均是对称的,因此本文选择偏学生t 分布(SkT)来准确刻画序列的非对称性,最后确定的边缘分布为ARMA(p,q)-GJR(1,1)-SkT 模型。具体形式如下:
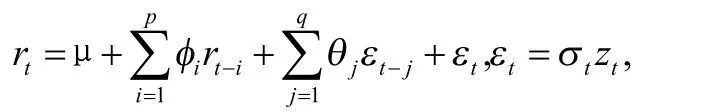
SkT v λ的分布函数为:

其中,

λ ∈( - 1,1)为偏度参数, v∈ (2, +∞)是自由度,T (⋅, v)是t分布函数。
2 藤Copula 模型
2.1 藤结构


一般地,由于(1)式分解不唯一,因此(4)式也随之有多种分解。
2.2 几类藤Copula 模型
由于藤结构比较复杂,因此本文采用R 藤矩阵法[16~18]来表示R 藤,联合密度形式为

藤Copula 模型的参数估计采用极大似然估计法,具体步骤为:首先根据最大生成树MST-PRIM算法[19]来选择藤结构,然后在每条边上利用信息准则确定Pair Copula 模型(在R 藤结构中,当所有的Pair Copula 函数确定为t Copula 时,称为R-Vine all t,其他类似),最后通过极大似然估计法计算出所有参数的值。在确定Pair Copula 模型时,本文选择AIC 与BIC 信息准则检验,计算公式为

3 滚动窗口VaR 度量及返回值检验
3.1 滚动窗口VaR 计算
风险价值(VaR)是指在一定时期内,给定的置信水平下,某资产组合预期可能的最大损失值。公式为
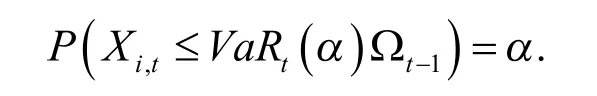

其中iω 表示资产 iX 在组合中的权重。
计算VaR 的方法有多种,这里采用能够反映具有动态时变特点的滚动时间窗口Monte Carlo 模拟法[11,16,20]来计算风险价值。计算VaR 的具体过程如下:


(iii) 在样本量保持不变的情况下,将样本区间向后平移一天,得到的新样本即为第911 日的估计样本,然后按照步骤(ii)和(iii),预测第912 日的VaR预测值。
(Iv) 反复进行步骤(Iv),就可以计算出第913 日、914 日直到第1210 日的VaR 值,即得到样本外300天的投资组合VaR。
3.2 Back-testing 检验

4 实证分析
4.1 数据选取与处理
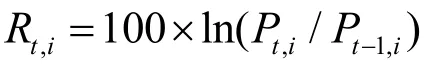
4.2 数据分析与参数估计
对整合之后的收益率数据做描述统计分析,从表1 的分析结果可以看到六只股票日收益率的峰度均大于零,偏度小于零,表现出典型的“高峰厚尾”、左偏的特点。从均值和标准差也反映出数据波动幅度很大。J-B 和LM 检验表明:每组收益率数据均不服从正态分布的假设,并且都存在明显的ARCH效应。因此不适合用静态的、非对称的分布来建模。

表1 原始数据的描述性统计分析结果 Table 1 Descriptive statistical analysis results of original data

表2 各序列边缘分布模型的参数估计结果 Table 2 Parameter estimation results of edge distribution model of each sequence
表2 给出了边缘分ARMA(1,1)-GJR(1,1)-SkT的参数估计以及模型的检验结果,可以看出在显著性水平为0.05 时,Q(5)与LM(3)检验统计量对应的p 值均大于0.05,不能拒绝原假设,即各残差序列均不存在自相关现象以及ARCH 效应,模型拟合较理想.将标准化残差序列经过概率积分化处理,使其服从0-1 均匀分布并参与藤Copula 建模。由于藤Copula 模型结构非常复杂,本文仅给出了R-Vine- Copula 模型首次滚动的结果,具体如表3 所示。

表3 R-Vine 首次滚动的RVM(左)与对应的Pair Copula 函数(右) Table 3 RVM (left) of r-vine's first roll and corresponding pair copula function (right)
表3 中展示了R-Vine 首次滚动的RVM 结构中节点排序和对应的Pair Copula 函数情况,第一层节点为(3,4)(4,2)(2,5)(1,5)(5,6)对应的Pair-Copula函数,为survival BB7(即表3(右)中对应(R6,C1)位置的数字19),survival Gumbel,BB1(Clayton Gumbel),t-,t-.其余层的节点和Pair Copula 也可以从表3 和图1 中看出。

图1 R-Vine 首次滚动的RVM 结构图 Fig.1 RVM structure of r-vine first rolling
由此可见,对于不同资产之间的相依结构可以灵活选择不同的Copula模型,理论上R-Vine-Copula较R-Vine all t刻画多元资产序列相依结构更具优越性。为了更直观比较几种藤Copula 的拟合效果,表4通过对数似然值及信息准则对模型进行比较。

表4 几类Vine-Copula 模型的拟合效果比较 Table 4 Comparison of fitting effects of several kinds of vine copula models
由表4 的结果可知:C-Vine-Copula 模型对应的AIC 值最小,BIC 值也比较小,说明C-Vine-Copula模型比其它模型更能描述序列数据之间的相关关系;R-Vine-Copula 比R-Vine all t 和R-Vine all Gumbel 拟合效果好,这是因为R-Vine-Copula 在选择 Pair Copula 时比较灵活,同时也说明R-Vine-Copula 拟合实际资产序列数据更加合理;从R-Vine all t 和R-Vine all Gumbel 模型的拟合效果比较来看,后者的拟合结果更令人满意,反映出了Gumbel Copula 比t Copula 更适合描述金融数据的非对称性。
4.3 模型VaR 预测效果检验
在计算投资组合VaR 时,首先考虑等权重的情形,即ωi=1/6,以前面910 天收益率数据为基础,利用滚动Monte Carlo 模拟法估计藤Copula 中的参数,在此基础上结合边缘分布通过反推得到模拟日收益率,然后运用滚动窗口反复模拟得到样本外300 天的VaR 预测值,经过设定不同的置信水平来比较VaR 情况。

表5 几类藤Copula 模型VaR 预测及Kupiec 检验结果 Table 5 VaR prediction and kupiec test results of several vine copula models
由于等权重计算VaR 与实际情况不太符合,因此为了体现模型的稳健性,本文采用Mean-CVaR约束条件,利用原数据的最后300 天收益率计算得到新权重,依次为0.1772,0.1831,0.2018,0.1609,0.1735,0.1035。再次计算动态V aR 并进行返回值检验,结果如表6 所示。
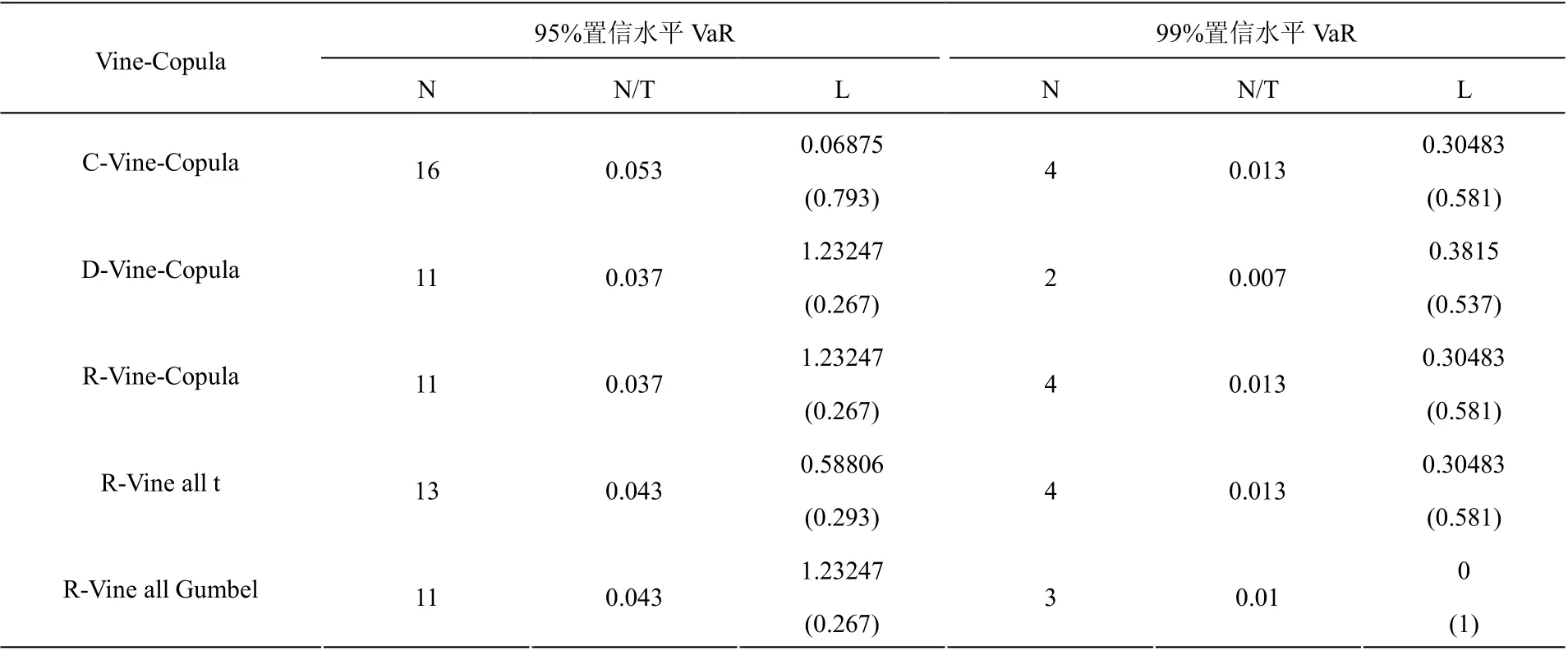
表6 新权重下藤Copula 模型VaR 预测及Kupiec 检验结果 Table 6 VaR prediction and kupiec test results of vine copula model under new weight
由表5 和表6 可得:5 种模型都通过了检验(括号中为对应的检验P 值),并且在两种置信水平与两种权重下,C 藤与R-Vine all t 在VaR 预测时表现出较好的稳健性,即失败天数保持不变。图2 展示了在新权重下C 藤的VaR 预测检验结果,从图中可知:随着置信水平的增大,VaR 值减小,也就是说资产投资组合收益率超出最坏损失的天数减小,即失败天数在随之减小。
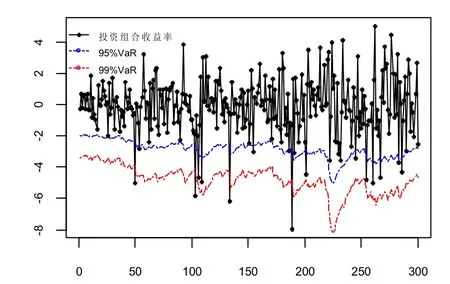
图2 新权重下C 藤的VaR 预测稳健性检验结果 Fig.2 VaR prediction robustness test results of C vine under new weight
5 结论
针对具有“高峰厚尾”的高维金融序列,本文选择具有时变特点的ARMA(1,1)-GJR(1,1)-SkT 模型、几类藤Copula 模型以及VaR 等理论,通过实证分析,证明了利用这些模型刻画金融序列具有实效性,为高维投资组合风险管理提供了理论依据。 经模型VaR 的预测与返回值检验结果可得出:不管是等权重还是新权重下,从整体上看,C 藤的预测效果最佳,其次是R-Vine all t,D 藤最差。而通过表4 模型检验的信息准则以及对数似然值显示:C 藤拟合最理想,R 藤次之,R-Vine all t 最差,这充分反映了C藤最适合解释多资产金融序列的诸多特性,而R 藤与R-Vine all t 在两次检验中反差如此之大,其原因是本文未进行详细的统计诊断,事实上R 藤在选择Pair Copula 时比R-Vine all t 更灵活,因此也更实用。计算VaR 方面,Mean-CvaR 约束条件比等权重更符合实际。

