P、Bi掺杂锐钛矿相TiO2的第一性原理研究

马战红，邓亚丰，任凤章，熊 毅

(河南科技大学 材料科学与工程学院，河南 洛阳471023)

0 引言

二氧化钛(TiO2)在理论上和试验上均已成为光催化研究领域的热点[1-4]。由于锐钛矿相TiO2的禁带宽度是3.2 eV，在实际应用中，只能被波长小于387.5 nm的紫外光激发，不能充分利用大部分可见光，需要将光响应范围扩展至可见光区。对TiO2进行金属离子掺杂可以降低TiO2的有效禁带宽度，引入的杂质能级还可以成为光生电子-空穴对的浅俘获势阱，从而促进光生电子-空穴对的有效分离，增加载流子的寿命[5-8]。引入适量的Bi元素可以有效地提高TiO2的光催化活性，如文献[9]使用溶胶-凝胶法制备Bi掺杂TiO2，通过检测发现掺杂适量的Bi可以明显提高TiO2在可见光范围内的响应。文献[10]计算表明：Bi掺杂TiO2后使体系在可见光范围的光吸收强度明显增大，同时使吸收带边发生了红移。近十几年来，TiO2体系的非金属元素掺杂改性已经成为研究热点[11-14]，引入适量的P可以有效地提高TiO2体系的光催化性能[11,15]。

第一性原理计算广泛应用于材料的结构设计和性能计算之中[16-17]，非金属和金属元素的共同作用可以改变TiO2在费米能级附近的电子结构，共掺杂后会出现电子自补偿作用，使杂质能级处于满填充状态，不仅可降低电子与空穴的复合，而且使TiO2的光学性能得以提高[18]。本文以P和Bi元素为例，系统研究P、Bi掺杂对TiO2电子结构及光学性能的影响。

1 晶胞模型的建立和计算方法

图1 P、Bi掺杂TiO2的4×2×1的超晶胞结构图

纯的锐钛矿相TiO2为四方晶系，每个晶胞由4个TiO2单元组成。P、Bi掺杂TiO2采用4×2×1的超晶胞结构，如图1所示，该超晶胞中共有96个原子。本文计算均基于密度泛函理论(density functional theory，DFT)平面波超软赝势的方法。在描述价电子与离子间的相互作用时，选取元素的价电子组态分别为：Ti，3p63d24s2；O，2s22p4；P，3s23p3；Bi，4f145d106s26p3。本文采用交换关联能为广义梯度近似(general gradient approximation，GGA)，赝势函数采用梯度修正函数(Perdew-Burke-Ernzerhof，PBE)，计算均在倒易空间进行。自洽过程结束时，结构的总体能量收敛于2×10-6eV/原子，每个原子上的力小于0.05 eV/nm，应力偏差为0.1 GPa，公差偏移0.000 2 nm。布里渊区K点设置为2×2×3。在计算能量时，电子采用的是自旋极化处理，由于GGA方法在计算电子结构时低估了一些金属氧化物的带隙宽度，采用GGA+U方法对能带加以修正[19]。本文所选参数为Ti的d轨道加5.5 eV(UTid= 5.5 eV)，O的p轨道加6 eV(UOp= 6 eV)。先优化晶体结构，根据所得结构参数再进行能带结构及光学性质的计算。

2 结果与分析

2.1 晶格结构和稳定性分析

表1 计算得到体系中TiO2的晶胞参数 nm

为了研究体系掺杂对锐钛矿相TiO2结构的稳定性影响，本文计算了纯锐钛矿相TiO2、Bi-TiO2、P-TiO2和P-Bi-TiO2的晶胞参数，其结果见表1。由表1可知：本文计算纯锐钛矿相TiO2的晶胞参数与试验值[20]非常接近。P、Bi单掺杂锐钛矿相TiO2的晶胞参数与文献[21]的试验值和计算值基本一致。由于Ti4+的半径(0.061 nm)大于磷离子的半径(0.017 nm)，而Bi3+的半径(0.103 nm)大于Ti4+的半径(0.061 nm)，因而导致掺杂体系中TiO2的晶胞参数发生变化，产生了晶格畸变。依据晶体场理论[22]，发生晶格畸变会导致TiO2晶体结构的负电荷中心与正电荷中心产生电偶极矩，从而在晶格内形成局域内部场。此变化可以促进光生载流子的分离，因而有益于提高TiO2光催化活性。

形成能Ef大小是判断体系稳定性和掺杂难易程度的重要依据。掺杂体系的形成能越小，表明掺杂体系稳定性越高，掺杂越容易实现。对于P-TiO2和Bi-TiO2单掺杂体系来讲，其形成能Ef的表达式[21]为：

Ef=E(doped)+μ(Ti)-E(undoped)-μ(X)，

(1)

其中：E(doped)和E(undoped)分别为掺杂体系、未掺杂体系的总能量，eV；μ(Ti)为Ti的化学势；μ(X)为掺杂原子的化学势，在共掺杂体系中，μ(X)=μ(P)+μ(Bi)。

表2 计算得到的掺杂形成能Ef

表2是本文计算得到的掺杂形成能Ef。由表2可知：3种掺杂体系的形成能均为负值，说明掺杂体系可以稳定存在。

2.2 掺杂对TiO2禁带宽度和态密度的影响

表3为TiO2掺杂体系的禁带宽度计算值Eg。由表3可知：锐钛矿相TiO2的禁带宽度计算结果为3.22 eV，这与资料报道的试验值(3.23 eV)非常接近[20]。图2是锐钛矿相TiO2的电子态密度图。由图2可知：O的2p轨道构成了锐钛矿相TiO2的价带，Ti的3d轨道构成了TiO2的导带，且锐钛矿相TiO2的价带和导带中都含有O的2p轨道和Ti的3d轨道成分，由此可以判断锐钛矿相TiO2的Ti原子与O原子之间存在部分共价键的成分，这与文献[23]报道的结果一致。

表3 TiO2掺杂体系的禁带宽度计算值Eg

图3为P掺杂TiO2的电子态密度图。由图3和表3可知：P的3p轨道与O的2p轨道发生了杂化现象，P单掺TiO2相比未掺杂体系的禁带宽度小。这是由于P掺杂后，形成了杂质能级，杂质能级可以充当电子由价带跃迁到导带的跳板，减小了电子由价带跃迁到导带所需要的能量。禁带宽度减小，将会导致吸收带边的红移，使电子由价带跃迁到导带所需要的能量有所降低；该杂质能级不是深杂质能级，不会成为光生电子的俘获中心，使得TiO2在可见光范围内的光催化活性得到较大程度的提高[11]。

图2 锐钛矿相TiO2的电子态密度图

图3 P-TiO2电子态密度图

图4为Bi掺杂TiO2的电子态密度图。结合表3和图4可知：Bi掺杂之后TiO2的禁带宽度变小，这是由于Bi掺杂后，出现一个比较小的态密度峰，这个峰对应杂质能级。这个杂质能级主要由Bi的6s轨道、O的2p轨道和Ti的3d轨道上的电子杂化而成，该杂质能级的存在使电子由价带跃迁到导带所需的能量大大降低。禁带宽度减小，将会导致吸收带边的红移，增加TiO2在可见光范围内的光催化活性。但是该杂质能级是深掺杂能级，且当Bi浓度太高时，容易成为光生电子-空穴对的复合中心，从而降低光生电子的利用率，导致体系的光催化性能大大减弱[13]。

图5为P和Bi共掺杂TiO2的态密度图。结合表3和图5可知：该体系的价带主要由O的2p轨道和P的3p轨道构成，导带主要由Ti的3d轨道构成，在带隙中间出现了由Bi的6s轨道提供的电子态密度峰，对应能带结构中的杂质能级。共掺之后材料的禁带宽度为1.83 eV，光吸收范围正好处于可见光范围内，有利于增加TiO2体系对可见光的利用率，从而增加其在可见光范围内的光催化活性。

图4 Bi-TiO2电子态密度图

图5 P-Bi-TiO2体系电子态密度图

2.3 光学性能分析

图6 P和Bi掺杂TiO2前后的吸收光谱

图6为P和Bi掺杂TiO2前后的吸收光谱。由图6可知：经过掺杂后，TiO2的吸收带边均发生红移，其中，Bi-TiO2的红移最为明显，禁带宽度最小；而P-TiO2和P-Bi-TiO2的光吸收相比于未掺杂TiO2的光吸收出现较小程度的红移现象，但是在可见光范围内；Bi-TiO2和P-Bi-TiO2的光吸收强度都比较大，说明这两个掺杂体系在可见光范围的光催化活性最好。根据能带和态密度的结果，可以认为掺杂后禁带中杂质能级为电子跃迁提供了一个跳板，使电子从价带先跃迁至杂质能级，再跃迁至导带，降低了电子跃迁过程中所需要的能量。

图7为纯锐钛矿相TiO2、P-TiO2、Bi-TiO2以及P-Bi-TiO2的复介电函数。介电函数的实部与虚部综合反映了材料对光的利用率。图7a为纯锐钛矿相TiO2的复介电函数。从图7a中可以看出：该体系的虚部在1.9 eV处开始有反应，表明该材料在可见光范围内的响应能力较差。图7b～图7d分别为P-TiO2、Bi-TiO2以及P-Bi-TiO2的复介电函数。从图7b～图7d中可以看出：与未掺杂的TiO2体系相比，这些体系的虚部峰值均出现红移现象，这是由于掺杂后体系中存在杂质能级，降低了电子在跃迁过程中所需要吸收的光子能量，导致复介电函数的虚部峰值发生向左移动的现象。Bi-TiO2的虚部峰值向左移动的趋势最大，但是在可见光范围内，Bi-TiO2的虚部响应数值低于P-Bi-TiO2的虚部响应数值，表明Bi-TiO2在可见光范围内的光催化活性低于P-Bi-TiO2的的光催化活性。

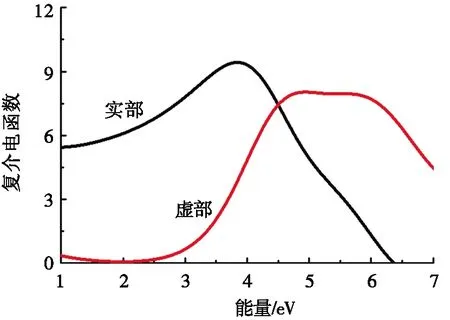
(a) TiO2

(b) P-TiO2

(c) Bi-TiO2

(d) P-Bi-TiO2

3 结论

(1)采用第一性原理计算得出纯锐钛矿相TiO2的禁带宽度为3.22 eV。

(2)从掺杂形成能的结果可以看出，P-TiO2、Bi-TiO2以及P-Bi-TiO23种掺杂体系均可以稳定存在。

(3)从能带结构及态密度结果可以看出，不论是P、Bi单掺杂或是共掺杂，均可以降低锐钛矿相TiO2的禁带宽度，共掺杂体系可以将禁带宽度降低至1.83 eV，大大提高了锐钛矿相TiO2在可见光范围内的光催化活性。

(4)与未掺杂锐钛矿相TiO2相比，掺杂过后锐钛矿相TiO2的光吸收带边均出现红移现象。