指南车控制理论的创建
邓崇林
(独立研究员)
一般在谈论指南车构造与原理时,人们通常会说指南车是一种具有负回馈作用并能定向的自动化机械装置[1],也有自动控制专著指出指南车应用了反馈原理的控制装置[2,3],甚至指南车机构设计专家在其文献中特别强调指南车是拥有负反馈机构的机械装置[4]。早期英国专研中国科学技术史的李约瑟说过指南车有负反馈回路自动控制[5],这或许是大家这么说的源头吧。但是,也有控制专家万百五持不同观点,他认为指南车是一个按扰动补偿原理工作的开环自动调节系统[6],该文从机械观点推论,差动齿轮系指南车乃依差动齿轮机械原理运作,它会形成闭环自动调节系统。万百五又在他的另一篇文章里补充了指南车应用了不变性原理[7]。
指南车的控制理论到底为何,其实还有其他不同观点,让人莫衷一是,这里就不一一赘述。总之,立论何以如此多样,究其原因仅有一个,就是指南车欠缺一个数学模型的控制理论,在没有可供推算的理论基础之下,便造成了现今众说纷纭的局面,因此,这就成了本文的研究动机。
1 研究对象与方法
谈到指南车的机械装置,这里先来界定一下本文讨论有关指南车的组成构件。指南车在实体上是由两侧车轮、传递装置、转向机构、车架、指向器等五大构件所组建而成的双轮无动力车辆。这里所涉及的传递装置与转向机构需要进一步诠释,其中传递装置乃由于车轮转动与转向机构之间有一段空间隔阂,为了填补此段距离以及进行运动传递和转速校正,该装置将会由齿轮、复合齿轮或齿轮对两两啮合组成;至于转向机构基本上是采用差动轮系机构,当然这是从机械机构的角度来看;倘若改用自动控制的角度,它将以机械构件做为基础在角速度方面的两个输入一个输出的控制器;如以功能作用的角度来看,当指南车行驶时,该装置会时时左右着车上指向器的转向,因此,特称其为转向机构,这是本文采用的术语,因为在推广至诸如不用齿轮也能控制指向器的指南车[8,9]时,名称的不变性,能保住控制理论的一贯陈述。
现在探讨指南车控制情况。首先,输入端利用适当的感知装置(同时运用左右两侧的车轮)不断地测量车辆行进中两轮滚动轧出不同轨道所反映的行程变化信号(ΔS),如站在维持特定方向控制目标来看,这些行程变量会带来方向维持上的干扰,因此称其为扰动信息或简称扰动,此刻感知装置一边进行输入扰动信息同时一边进行信息转换发出两车轮角速度差速(Δω)之前馈(feed forward)信息并立刻反应给传递装置与转向机构,又在量测扰动当下,由于所有装置混在轮车架里头,当扰动被量测时,车轮也推驶着车架,从而车架即刻产生旋转角速度变量(Φ),它会连带使得受控对象指向器为之改变原方向,从控制原理来看,这就是干扰信息,但在方向刚要被影响的那一瞬间,指向器立马收到来自转向机构所发出的控制信息(Ω),指向器自然受到双方通道影响,当会调动控制信息以补偿干扰信息,也就是调合(Φ+Ω)成为系统的控制要求,理论上最优解当然是零,这也就成了最优化控制条件,也称作不变性原理[7],持续不断依此控制,指南车始终能够克服扰动,从而使输出方向变量保持稳定不变。原理上,指南车如设计妥当,在理想运动状态下,无论做任何方向行驶,其指向器仍永远保守着既定的方向,这就是整体指南车进行自动控制的过程。以下就用一张藉指南车组成构件之间信息互动来说明指南车前馈控制的概要图。
从图1中可以辨别出这是双通道开环控制,由于输出方向变量并不发出反馈信息,因此指南车自动控制所起的作用是预先量测扰动,实时进行补偿防止扰动的扰乱,实属按扰动产生补偿作用进行调节的前馈控制(Feed Forward Control, FFC)系统,这就成了本文要研究的对象。

图1 初步建立差动式指南车前馈控制机械模型框图
有了前述依实况分析建立差动式指南车机械控制模型这个基础,就能运用古典控制理论方法建立指南车自动控制系统的数学模型。为了达成这个目标,首先,从图1探出指南车控制系统是双通道结构,然后根据系统双通道结构及工作原理将系统分成若干个环节,接着推演出每个环节各自的数学模型,并求取各环节的传递函数,再从相加点切入,分进合击之下,按信息流向依次连接成整体方框图,既建立了控制系统方框图,并依最优化控制条件或不变性原理求出指南车设计规律。后续还会以实际指南车设计案例,进行控制和机械方面的相互验证,并加以推广,还要对常见误区加以探讨,进而厘清一些长久以来混淆不清的观念,以上就是本研究的方法概要。
在落实研究方法之前,有些前提假设在这里预先提出来,本文推论都是基于这些假设。一般机械专家在设计指南车时,皆以运动学为基础分析指南车在纯滚动条件下,运用所设计的机械构件传动比的线性特性,计算出构件之间角速度的传递关系,从而算得指南车上指向器角速度与两侧车轮角速度差的数学关系式,最后获得指南车的设计要求。本研究沿用前述惯例,以自动控制的观点创建指南车理想化模型在平面上运动的控制理论,即把指南车视为理想刚体同时不考虑指南车重量、施力、转动惯量、力矩等力的作用,运用机械线性构件并排除诸如背隙(backlash)、不平滑、齿形误差、组合误差等非线性因素,且两侧等径车轮在车辆运动时皆保持垂直立于平面上纯滚动,同时两轮之间的轮轴与转向机构上的指向器也在平行于地平面的两不同平面上运动,此时刚体的任意转动,由原来欧拉角表征的章动、进动和自旋三部分运动,在这些理想约束条件下,简化成为平面上单一自旋角速度运动,从而让指南车形同刚体在平面上的运动,进而找出其控制规律。
2 指南车保守指向的运动分析
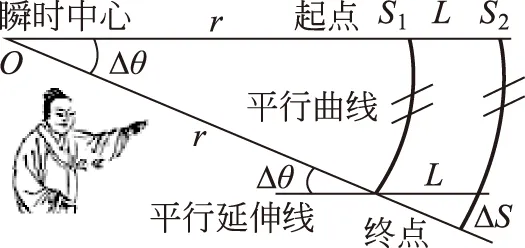
图2 车架瞬时行驶轨迹在平面的几何图
本节首先是弄清楚指南车形同刚体在平面上的运动现象,即探讨车轮行进轨道、车架转角与指向器的变化情形,目标就是要建立起有关的数学模式,以利后续找出其控制规律。现有一辆双轮的轮轴间距长为L之指南车,以车头前进方向为准,由于两轮径等高又车轮直立于平面且轮轴构件两端垂直衔接车轮,于是轮轴构件可垂直投影到两轮与平面接触点的连接线段,以俯视平面角度来看它们是迭合相等的,因此该连接线段的距离也是长L,所以车架的平面运动也等于是该连接线段的平面运动,是等价的。今考虑当车架在某瞬时Δt,于地面某一处观测点O产生旋转角速度Φ,形成角位移Δθ,因此依角速度定义知Φ=Δθ/Δt,又此瞬时观测点之速度为零,以刚体平面运动来论,可将它视为瞬时零速度中心之基准点,其轮轴相当于一条两端长L构件的刚体,而构件两端点速度的垂直线就是轮轴的延伸线,速度瞬时中心出现于速度向量的垂在线,因此刚体上任意点的瞬时角速度全等于车架角速度Φ,在此瞬时其左轮2与右轮1行驶于平面上滚轧分别留下两条轨道圆弧S2与S1,如图2所示,则两轮起点延伸线与两轮终点延伸线必相交于瞬时中心O且夹角正是Δθ,其行程差为两圆弧相减(ΔS=S2-S1),且圆弧S1与O基准点始终保持着等距r的关系,又圆弧长度为瞬心切线速度乘以此瞬时时间,且瞬心切线速度的求得是以瞬时中心之距离半径乘上角速度,因此,行程差就等于不同距离半径乘上角位移的差额,其计算过程为:ΔS=S2-S1=(r+L)Δθ-rΔθ=LΔθ,再将两边同除以瞬时时间可得到下列数学关系式:
ΔS/Δt=L(Δθ/Δt)=LΦ(t)
(1)
式(1)是指南车行程差与车架旋转之切线运动关系式。今改用几何观点来看,取S1终点处另画一条辅助平行延伸线与两轮起点延伸线相互平行的话,那么两轮起点与此辅助平行延伸线之间,所分割出来的是平行的两条圆弧线段,是等长的,所以,原来的行程差先对消该平行分割曲线之后,就只剩下是取S1终点为原点,并于轮2在S2曲线分割后所剩余的轨道上,用车轮轴间距(L)当半径所画的圆弧线,且夹角仍为Δθ,由于欧氏几何上平行曲线的特性,证明了ΔS=LΔθ关系式,也验证了式(1)数学关系式成立,如令指向器于指南车起点启动时的方向,就是沿两轮起点延伸线的车架方向,也就是图2中人偶左手所指之方向,那么它在某瞬时驱驶车架拐弯Δθ夹角,就等于是车架轮距当半径于这期间内产生旋转角速度变量(Φ),这两者乘积就相当于是车架以右端点为原点于左端点沿切线方向运动之切线速度。其车架两侧双轮单位时间之行程差仅仅与车架拐弯角速度成正比,且这比值恰等于车轮轴间距,这是第一个描述指南车两轮行驶于平面上的切线运动方程式。此时指向器若没有进行补偿动作,则其方向会旋转Δθ角而偏离原方向,倘若要指向器保持原来启动时的方向,则必须同时间内反方向补偿旋转角速度Ω(相对于车架),于是要能满足下列约束条件才行:
Ω(t)=-Φ(t)
(2)
这是第二个指南车设计指向器运作所要求的完全补偿公式,由于等量反向关系,使得指向器相对于地面的角位移永保为零的状态,这样指向器就能持续保持着单纯平移运动而不随车转,使其守住指向维持不变。如把这个式(2)改成左右项相加为零,同时将差分符号改成微分符号,就成了指南车保守指向运动方程式,这在另一文献[10]称之为“自由平移方程”,由于在前一节的假设已给出指南车形同刚体在平面上的运动,根据运动的叠加原理,刚体平面运动可看成是刚体的平动与转动的迭加,又前述文献[10]已用微分几何证得指南车在平面上的运动完全与选取路径无关,这样分析指南车在平面上的运动现象,就能化简成刚体在平面上的转动而已,因此,本节只需考虑车辆转弯的运动学就足够了。另,一般机械专家在设计指南车时,都直观默认不考虑刚体在平面上的平动(不一定是直线运动),而在车辆转弯时只单方面考虑圆周运动[11,15],这在理论建构上是不严谨的,因为有关刚体在平面上的平动之所以毋庸考虑,靠直观或辩证(这也是如今指南车控制立论多言堂的情况)是不准确的,而是需要运用数理加以证明。为了增进对指南车运动学的广泛认识,这里额外(不在本研究范围)将指南车在平面上的运动加以推广,当指南车行驶于曲面时,它的指向运动就会与路径选取直接关联,这部分也是由前述文献[10]给出严格证明,这应该是一般指南车设计专家料想不到的应用。
3 建立双通道的数学模型
从第1节分析知道,本文研究对象指南车控制系统是双通道结构,接下来将接续第2节的阶段分析成果,分别建立干扰通道与控制通道的数学模型。
3.1 建立干扰通道的数学模型
以控制观点来看,干扰通道中的主要执行者乃轮车架构件,其运作原理有一点儿复杂,须先厘清,才能求出此环节的数学模型。首先针对指南车运动现象进行观察车轮轨道变化的各种有用物理量,我们把观察目标放在两个车轮滚动造成行程差ΔS′,这个部分是来自两轮有着旋转角速度差Δω所贡献的,由于是来自于Δt期间内两轮以不同角速度在路面形成车轮切线速度Vt所经过的长度差,因此如果两轮同为R半径时,由两轮切线速度差可求得两轮滚动行程差ΔS′的关系式如下所示:
ΔS′=(Vt2-Vt1)Δt=(ω2-ω1)RΔt=ΔωRΔt
(3)
假设指南车行进间车轮始终是以纯滚动方式运动,也就是令车轮自旋与行进轨道之间起到了完全耦合作用,简称为车轮的“自旋-轨道耦合作用”,那么就保证了在单位时间内车轮滚动行程差式(3)等于平面上式(1)中的两轮平行轨道曲线长度差,也就是满足了下列纯滚动行程差恒等关系式:
ΔS′=ΔS
(4)
接着把前面式(1)转换成Φ=ΔS/(LΔt)的关系式,将此结果再除以这个把式(3)借助式(4)所转成Δω=ΔS/(RΔt)的转换关系式,再将Φ与Δω相除结果经分子项与分母项两两对消除掉重复变数,经此整理后得到下列车辆几何特征与车转变量的数学关系式:
(5)
从式(5)数学关系式里已经看不见行程差变量,也就是原先量测物理量是两轮行驶平行轨道行程差对时间的变量ΔS/Δt在纯滚动条件下,已经自然地调整化为两轮旋转角速度差Δω,导致前面所建之图1差动指南车前馈控制机械模型图中,要把输入控制系统的扰动改成Δω,在干扰通道中有一个环节是依式(5)的数学模型在进行信息转换。将式(5)两边取拉普拉斯转换,可发现输入量F(s)与输出量之间是比例关系,由此可求得干扰通道上之传递函数为GD(s)=R/L。
3.2 初建控制通道的数学模型
以控制观点来看,控制通道只有左右侧两车轮的转速差当输入,除此之外,并无其他干扰因素或设定值介入执行机构,至于输出则只有一个指向器进行补偿作用的角速度Ω,所以补偿角速度可表成是两轮转速差的函数,也就是Ω=f(ω2-ω1)=f(Δω),在分析时,前式函数f为执行控制设备专有的特性机制,它不随着过程控制的变化而有所改变,又由于齿轮机构传动比之线性特征,这可进一步推算出整体转向系统的等效比值,用黑箱慨念当它是该系统的特性参数,并定义成一个β符号代表,把β比例因子界定为补偿因子(compensating factor),它是用来补偿车子转弯所生的方向偏差,因此函数f会是个线性函数,也就是下列两轮角速度差额与指向器自转变量的数学关系式:
Ω=f(Δω)=βΔω
(6)
同样将式(6)两边取拉普拉斯转换,可发现输入量与输出量之间是比例关系,进而求得控制通道之传递函数为β。又由于该通道中是由传递装置与转向机构所组成,而β与前述两种设备都是具有传动比特性,即同样都是比例值。同理,可将控制通道拆分为传递装置之传递函数为GT(s)=NT与转向机构之传递函数为GC(s)=βC,其中NT是传递装置转速比,有着把扰动Δω转成适当转速的校正作用,以便匹配转向机构的输入特征,因此NT称为此校正环节的校正因子,至于控制通道主要执行控制者乃转向机构,控制环节就是由它所构成,因此转向机构正是掌管这个环节的控制器,它的补偿因子就是βC,显然有β=βCNT关系式,至于这些因子的内涵将于第4节里讨论。
4 建立指南车控制理论——前馈控制系统与计算法则
本节将回答如何设计指南车以求达到式(2)要求,也就是调合(Φ+Ω)输出值始终是零。注意,在后续式(8)是依图1里的信息流建立相关响应。由于第3节已求得干扰通道的传递函数GD(s),以及控制通道中校正环节的传递函数GT(s)和控制通道中控制器的传递函数GC(s),现整理如下:
(7)
现把扰动量F(s)输入到图1系统并经双通道进行控制,则总体输出响应输出量的Y(s)为下列关系式:
(8)
为实现前馈补偿控制之完全补偿条件,也就是令式(8)化为Y(s)/F(s)=0的情况,由于输入项F(s)不为零,为了让扰动对系统输出的影响为零,则需满足不变性原理[7],使得式(8)中传递函数项为零,即
GD(s)+GC(s)×GT(s)=0
(9)
将上式重新整理得:GD(s)=-GC(s)×GT(s),并还原成由式(7)各环节所组成的比例因子,可算得:
(10)
在设计要求时不用计负号。
上式“-”号乃表示补偿作用。当控制做到式(10)时,会把式(5)车转变量,用式(6)反向等值的控制变量加以抵销,即满足了式(2),使指向器方位不变。以下将图1转成由各比例因子构成的控制方框图
注意图3里控制通道中控制环节乃由差动机构行“-”号补偿因子的补偿作用,该作用能自动调合来自干扰通道的车转变量与指向器的角度变量始终为零,指南车也就达成了使命。此处终于推导出为达到完全补偿作用这个控制目标的控制系统设计要件,使得扰动对系统输出的影响为零,也就是让指向器有着保守指向作用的设计要件,正是由毋庸考虑负值的式(10)所规范,这里就以最有名的设计案例进行说明。英国学者兰开斯特 (G.Lanchester) 在1947年2月于伦敦中国学会中一篇名为“The Yellow Emperor’s South-Pointing Chariot”的演讲中,用直立式差速齿轮装置设计出具有指南功能的指南车,由文献[10]得知其输出入角速度特征为Ω=Δω/2且采等齿传递装置,依据式(6)与式(10),算得βC=1/2,NT=1,β=1/2,以及其几何特征为L=2R,也就是指所设计的指南车其轮轴间距一定要等于车轮直径。又为了能进行通盘计算,接下来要发展指南车控制理论的计算法则。

图3 指南车开环前馈控制系统框图
综观指南车的转向机构乃两个输入、一个输出的特定设备,一般在设计指南车时,由于转向机构左右输入转速通常不对等,这将反过来要求两侧车轮输入的传递装置传动比之设计也要有所不同,也就是左右侧输入端会有不同传动的转速比NTL与NTR,能对车轮转速与转向机构之间的匹配起了不同校正转速作用,这也就是为什么传递装置的控制环节称作校正因子的缘由,但如此一来,将会让前述图3控制系统方框图里存在单一项校正因子的转速比NT看起来好像不大对劲,这时前述控制理论是否还能适用,这成为本节要来解决的实际问题。
指南车控制理论的计算法则是这样子的,在机械传动系统中,传动比乃输入端主动轮与输出端从动轮的角速度或转速的比值,且传动比反比于齿数比,即ωi/ωo=Ni/No=Zo/Zi。当指南车原地打转一圈,这同时指向器刚好会自转一圈或兼有公转一圈,我们有兴趣的焦点皆围绕在“一圈”的问题上,如做不到或超过了“一圈”时,我们就要在设计阶段加以校正,让实际运作时使轮车架旋转与指向器自转都能同步且彼此反向转一圈,又由于我们有兴趣的是想搞清楚当输入一圈,经调控之后会输出多少圈的比例控制特性,因此要将原机械惯用计算方式的转速比之分子分母倒过来看成NT≡No/Ni=Zi/Zo,又分子分母里的单位时间可约分消去不计,使得这个转速比变成了圈数比,换言之,原本从机械观点计算输入与输出角速度比例过程,转变成计算输入一圈会输出几圈的控制响应,本文特称此为“输入转一圈”的计算法则,其适用范围涵盖控制通道里各种环节的比例因子。注意,这个计算法则迥异于机械观点,各种比值需倒过来看,有机械方面基础者,特别需要观念转换。又为了符合左右输入特性的差异,我们将分别固定单一侧车轮,使得指南车整体由两个自由度命题,变成一个自由度的一左一右两个各别命题,这样,左、右两侧各别输入经控制各环节的比例因子或许会有差异,然而整体控制通道的响应却是一致的,包括方向一致、大小一致,因为都得要满足不变性原理,也就是统一针对干扰通道的进行完全补偿动作,于是有了下列关系式
(11)
这时,图3系统方框图还是没变的,只有图内各比例因子的变量符号的脚注有些许变动而已。除了整体方框图不变之外,也可以求得左右侧不对称传递装置控制下的整体角速度输出入关系式,只要将式(11)代入到式(6)中,接着拆分成个别轮子其自带角速度的关系式,进而得到整体的角速度特征公式,得
(12)
上述公式乃线性组合的函数关系,这也额外验证了线性系统的叠加原理(superposition principle),即系统整体输出的响应是对各个讯号响应的代数和。对于这样有限的文字陈述,或许突然会看不明白,以下会用数学语言进行描述并自洽性证明了式(6)的线性系统假设,其推导过程如下:
有些机械书籍对轮系的自由度有所讲究,例如轮系中至少有一个齿轮除绕自身轴线转动(自转)外,其轴线还绕另一个固定轴线作公转,这种轮系称为周转轮系。周转轮系中自由度为1(两输入端其一固定)的称为行星轮系;自由度为2的称为差动轮系。这些名称虽有所不同,然而只要是同一种类的差动轮系机构,不管其自由度为何,其传动比都是同一个公式,如命题是自由度为1时,就是要找出该机构里哪个构件是固定不动的构件,然后在公式里将该构件对应的角速度设为零就行了。

图4 基本行星齿轮机构立体图与剖面图[12]
5 用物理及机械观点对行星齿轮机构进行运动分析
行星齿轮组(planetary gearset)是齿轮结构的一种,通常可分为简单行星齿轮系和复杂行星齿轮系。这里谈的是简单行星齿轮系中如图4所示基本的行星齿轮系(basic planetary gear train),分别有一个太阳齿轮(sun gear),一个环形的齿圈(ring gear),一个行星齿轮(planet pinion)和一个装有行星齿轮的行星架(carrier) 等4个基本构件组成,其中,太阳轮、齿圈和行星架三个构件共同绕公共轴线回转,而安装于行星架上的行星轮其外沿与齿圈相齿合,至于其内沿则与太阳轮相齿合,由于其绕行轨迹既可绕其本身轴线自转,又可在齿圈内绕公共轴线公转,就像行星绕着太阳公转一样,因而得名。
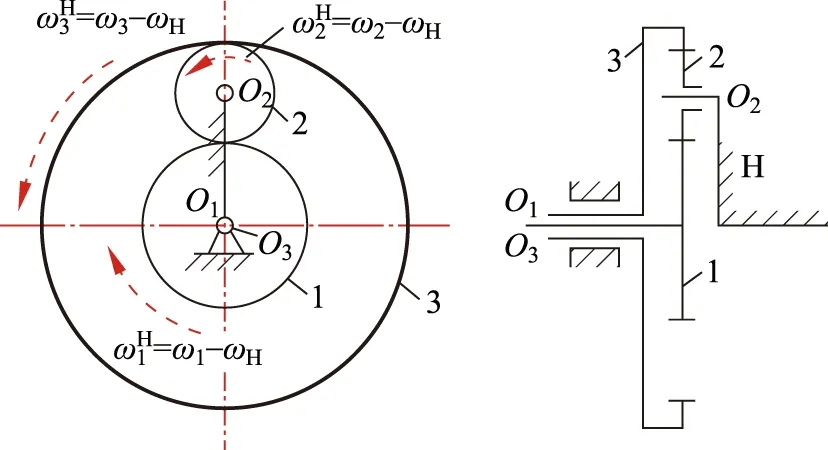
图5 在行星架的转动坐标系上观察到各构件相应的运动
在讨论运用行星齿轮系设计各种指南车之前,先就此一基本行星齿轮系进行基本的运动分析。这里将太阳轮、行星轮、齿圈和行星架等4个构件依序分别标记为1、2、3和H如图5所示,而各构件所相应的转动角速度则为ω1、ω2、ω3、ωH,以及半径各为R1、R2、R3,以下将进行物理运动学上的剖析。首先,吾人考虑观察者是落在行星架H的转动坐标系上,此时,可观察到行星架是静止不动的,这相当于在整个机构中的各个构件上同时加一个相同的(-ωH)相对运动角速度,则不影响各构件之间的相对运动关系,此刻各构件相对于行星架H的相对角速度(或转速)分别为
(13)

(14)
这里所谓的齿轮半径是指节径(节圆直径)的一半,而节圆(pitch circle)则是指两相啮合的齿轮在节点形成滚动接触的圆,其中,两相啮合的齿轮,其节圆相切之点即为节点(pitch point),又由机械设计齿轮的规范得知,模数(module)用于表示公制齿轮之大小,为节径(以公厘为单位)与齿数之比值,因此,模数越大,齿形越大,如果两齿轮之间要相互齿合的话,则两齿合之齿轮必须有相同的模数,换言之,齿轮之齿数与其半径成正比关系,从而由式(14)可推得
(15)
(16)
6 按机械原理探讨指南车的特征公式与控制特性
由于指南车转向机构需要二输入一输出的2自由度机构,在运用行星齿轮组设计时,行星齿轮组将被视为负号差动轮系机构,在其齿圈3、太阳轮1和行星架H等3个基本构件中,设计所选定的构件i和j都是活动构件且当作两个输入件,则第三个构件k将作为输出件,(i,j,k)∈{1,3,H} 并且i≠j≠k,则此差动机构将受到转化机构传动比式(16)所管控,又所有齿轮的齿数都是已知,使得该传动比为一常数比例项,再把式(16)经过角速度分子项、分母项与常数比例项交叉相乘并移项整理之后,能将该式(16)转换成ωi、ωj和ωk所构成的三元一次方程式,并令输出件其角速度变量ωk的系数为1,于是简化可得到

(17)
上述公式中的αi和αj皆是线性组合的正值常数系数,它们与“±”号都是由实际计算而定。接着考虑符合指南车指向要求而配套的传递装置,这可用定轴轮系方式求出其传动比大小为何,当然这也是个比例常数,进而可求出从左右两轮输入角速度ωL与ωR,分别经过左右两侧传递装置,一直传动到差动齿轮机构的输入件i和j的关系,如果这个设计是直接把指向器固连到输出件k的话,那么就可求得该指向器输出Ω角速度,以及相关输出入角速度之间的关系式,此推算结果其实是与第4节之计算法则里进行左右轮单独计算校正因子是一样的,毕竟这些因子都是传递装置的机械特性,最终可得出下列联立方程组
①ωi=±NTLωL,②ωj=±NTRωR,③Ω=ωk
(18)
上述公式中的“±”号是由实际计算而定,至于比例因子NTL和NTR也会是个正值常数,接着再将式(18)代入式(17),便能消掉ωi、ωj和ωk变量,转而成为指向器输出Ω角速度与左右两轮角速度输入ωL、ωR的关系式
Ω=αiNTLωL-αjNTRωR
(19)
以上是采左视指南车左车轮的顺时旋转方向为正向当基础的结论,后续讨论指南车相关角速度计算时都是以此为正负方向的依据,因此Δω≡ωL-ωR。现考虑指南车在平面上进行直线运动,此时的指向器将是纹风不动的,表示指向器并不会跟随指南车直行而发生转动,也就是指向器Ω角速度输出值必为零,而此刻处在直线运动的左右两轮角速度两者大小相等且转向一致,再将这些直线运动条件代回到式(19),导致该式中ωL、ωR的相关系数必须相等,并令此系数为γ,也就是
NTLαi=NTRαj≡γ⟹Ω=γ×Δω
(20)
由于是同一台指南车,所观察到的指向器输出角速度与左右两轮角速度差的关系式(6)必然是等同于式(20),故γ=β,也就是此系数乃前述第4节控制理论的补偿因子,进而能够推得式(11)与式(20)是一样的,故αi=βCL,αj=βCR,于是
(21)
式(21)有着二进一出系统特征,由于只涉及角速度变量,因而特称为指南车的角速度特征公式,这项由机械原理所推得结果,居然与控制理论推得的式(12)一模一样,这说明了,此角速度特征公式乃让指向器起到抵消车架偏转量的补偿作用;而此前不计负号的公式(10),则掌管着车轮半径与轮轴间距相关尺寸的几何关系,因而特称为指南车的几何特征公式,而该比值会受到补偿因子的约束。
接下来,我们回归本文关切的控制议题。首先来谈反馈控制,所谓反馈就是将输出的结果回输到原系统,但是在本节采机械原理推导过程中并没有发现把输出角速度重新导入的计算,而且这个反馈控制的重要特征也没有出现于式(21)里头,更何况该角速度特征公式本身会说话,它说明指南车的指向器角速度与两轮角速度差只跟控制理论中的补偿因子和校正因子相关,而这些比例因子皆属于指南车开环前馈控制自动调节系统中控制通道的各种环节。回顾本文在控制理论建立之初,是先假设了式(6)中有个补偿因子β,尔后才陆续推导出各环节的比例因子;反观本节则是先从探讨差动机构的传动比入手,再逐步探讨之后才发掘指向器角速度与两轮角速度差额的比例常数乃是补偿因子β,换言之,前馈控制起到了按扰动进行补偿作用,这也证实了先前式(6)的假设是成立的。无论是采机械原理观点还是控制理论观点,终究都一样,其表征皆需符合物理运动学的规律,其补偿作用则源自于前馈控制,因此,藉由行星齿轮系建构的指南车并不存在着反馈控制的机制。
综观本节所做理论推导,是建立在行星齿轮系组成构件任意组合情况下进行的,而行星轮系中做为输出入件就是齿圈、行星架与太阳轮等三种构件,其不同组合情况有三,分别为:(1)以行星架为左侧输入、太阳轮为右侧输入而齿圈为输出;(2)以齿圈为左侧输入、太阳轮为右侧输入而行星架为输出;(3)以齿圈为左侧输入、行星架为右侧输入而太阳轮为输出。由于本节推论必需透过实际设计案例进行检验,才能得到客观认证,因此,后续将会就这三种不同组合构件进行案例验算。
7 以实际案例进行控制和机械方面交叉验证
本节将以谢龙昌等[14]学者以差动机构周转轮系所设计之例3指南车做为设计案例讨论对象,其输出入件为第6节的①以行星架为左侧输入、太阳轮为右侧输入而齿圈为输出的组合情况,此处分别进行控制以及机械方面的计算,以便交叉相互验证。
7.1 以控制理论角度计算

图6 谢龙昌等设计例3指南车机械结构剖面图
图6是以“谢龙昌例3指南车”为例,进行理论方面验证。现令左轮不动仅右轮顺时旋转,此时先把焦点放在指南车里头的转向机构,由于左轮不动,使得该转向机构的4(80)行星支架齿轮被咬死,导致该行星支架也不会转动,因此,当该转向机构最底部的2(24)固连(32)太阳轮一起转一圈时,会经5(24)行星轮的惰轮作用将一圈24齿数传递给内有72齿的3(72)齿圈,也就是固连在该齿圈中心轴上端的指向器会旋转24/72=1/3圈,因此求得右输入的βCR补偿因子为1/3。接着来分析传递装置在右轮会发生什么情况,当右轮顺时旋转输入一圈时,由于会经过相同齿数的齿轮传动,也就是右轮传递给该转向机构的圈数比为NTR=1,这样从左轮不动仅右轮单侧旋转输入一圈就可以求得控制通道之传递函数为
(22)
现依指南车控制理论可进行两项推论,分别为:
(1) 当右轮顺时旋转输入一圈,同时会使指向器顺时旋转1/3圈。
(2) 而且式(22)须符合式(10)指南车的尺寸要求,即得R/L=1/3,也就是该指南车两轮之轮轴间距L必须设计成车轮半径R的3倍,这与图6设计纸上底部绘制长度水平线上头为两直立车轮之轮轴间距所标的注记:L=3r完全一致,而车轮半径标注则是绘制在图6右半边右车轮外侧的长度垂直线旁,其半径标注正是r。
现在俯瞰指南车以车架左侧轮不动当支点为圆心,做原地逆时针打转动作,此时右轮是顺针旋转,又车轮转一圈所走的长度就是车轮自转一圈的圆周长为2πR,且由前面算得两轮轮轴间距L=3R,当下若令左轮不动仅右车轮顺转3圈,这时右轮所走的轨迹长度,刚好是轮轴当公转半径绕满左轮支点圆心一圈的圆周长(3×2πR=2×πL),所以当右车轮以轴心顺时自转3圈,轮轴也绕左轮支点逆时公转一圈,这同时指向器在车架上顺时自转一圈,车架逆时公转与指向器顺时自转两相抵销,换言之,在地面可观察到,车架转弯当时,指向器的指向维持不变。

图7 基本行星轮系机构剖面图
接着考虑右轮不动仅左轮转动的机构各部件相应转速计算,由于此时多种构件相互啮合传动会比较复杂,为了化简复杂性并突显出做为控制指向器当主体的转向机构,还是把焦点放在图6指南车里头的转向机构,并将该转向机构里重复出现且不影响计算的齿轮元部件拿掉,仅留下与问题计算相关的组件,如此去枝蔓留主干,就精简成了如图7所示的基本行星轮系机构,或称之为等效控制器,注意,不要被该图标准的基本行星轮系所误导,该图里的2(24)太阳轮固连一根中心轴朝上,这是基本行星轮系的一般标准制图法,虽与图6谢龙昌等设计的例3指南车机械结构看起来会有所不同,但两者输出入的传动比是一样的,并不影响接下来的计算。此时,由于右轮不动,会将图6该转向机构中心底部的(32)齿轮咬死,也就是图7等效控制器中央2(24)太阳齿轮也不会转动,其输入从左侧4(80)行星支架为主动轮,当它转一圈时会带动5(24)行星齿轮绕着中央固定的2(24)太阳轮公转,这同时也诱发了行星齿轮自身的自转运动,又因行星轮与太阳轮两者齿数相等,使得行星轮会同向发生公转与自转各一圈,其中自转运动会将其24齿数传递给外围的3(72)齿圈,并导致其同向旋转24/72圈,该行星齿轮同时也会公转一圈,这将额外带动外围的齿圈同向转一圈,因此求得左输入的补偿因子为βCL=24/72+1=4/3。又从图6可看出左轮顺时旋转一圈时,由于会让20齿的(20)正齿轮反向转一圈传动给80齿的4(80) 行星架顺时旋转,也就是左轮传递给该转向机构的圈数为NTL=20/80=1/4,这样从右轮不动仅左轮单侧旋转一圈就可求得控制通道之传递函数为
(23)
有了前述右轮不动仅左轮顺时旋转下算得控制通道其传递函数为式(23)之后,发现其值与左轮不动仅右轮转动所得式(22)完全相同,这正如指南车控制理论所预测的式(11)一样,现依该控制理论可进行以下两项推论。
(1) 将它放入图3指南车控制方框图中,且必须符合不变性原理,即它要等于干扰通道的传递函数GD(s)=R/L,如不考虑负号的话,可算得同理论所预测的式(10)那样

(24)
以上依指南车控制理论推导出如何设计该款指南车其轮车架的几何条件,也就是该指南车左右两轮之轮轴间距L必须设计成该车轮半径R的3倍,这与图6该款指南车机械结构剖面图中为轮轴间距所做的尺寸注记:L=3r完全一致。
(2) 由于右轮不动当支点为旋转中心,此时若左轮顺时旋转一圈的话,会使得指南车轮车架逆时公转,同时指向器顺时自1/3圈,又车轮转一圈所走的长度为2πR,且两轮轮轴间距L=3R,使得左车轮自转3圈所走的长度刚好是轮轴绕满左轮支点圆心一圈的圆周长(3×2πR=2×πL),所以当左车轮以轴心顺时自转3圈,轮轴也绕右轮支点圆心逆时公转一圈回到原出发点,这同时指向器也在车架上顺时自转一圈,指向器与车架这两者是同步完成一周圈的,但两者旋转方向刚好相反,也就是这两者控制效果叠加起来始终相互抵消,充分体现出不变性原理的真谛,使得平面上指南车其指向器保守着方向上的守恒律,完全符合指南车平面上运动方程的描述[10]。
以上是以“谢龙昌例3指南车”[14]为样本,进行本文控制理论方面的验证。观察前述左轮不动仅右轮转动所得到的式(22)比例因子,以及右轮不动仅左轮旋转所算得的式(23)比例因子,这两者虽然βCR≠βCL,NTR≠NTL,即个别的控制节点有着不同的比值,可由式(11),将式(22)或式(23)补偿因子代入式(6)后,可推算出其指向器角速度Ω与左右两轮旋转角速度差Δω的关系式
(25)
上述结论若是按照机械原理针对图6该款指南车机械结构进行计算,其分析计算过程繁琐且复杂又容易出错,这需要机械专业功底才能算得式(25)关系式。由于式(24)的几何特征与式(25)的角速度特征完全与该款指南车原设计文献[14]要求完全一致。此处示范如何运用控制理论的推理路径,以不同于机械观点的逻辑检验了图6该款指南车的机械机构设计是正确无误的,同时也体现了指南车控制理论做为检验工具的简易性,方便在指南车于早期机械机构设计时间检视是否发生错误,避免在实际制作过程可能发生的设计错误或标注错误。
7.2 以机械原理角度重新计算
在前面我们将图6谢龙昌例3指南车里的转向机构简化为图7所示的基本行星轮系,这是有另一层用意的,因为这些机构都被研究透彻,其传动特性是有资料可查的,但前提是要以通用标准机构形式来查阅,为避免误判,此处就是以图7标准的基本行星轮系查阅了机械设计手册[13],得其传动比计算公式正如前面的式(16)所示,如采机械机构设计角度则要同时以两个输入一个输出来计算传递相应的角速度或传动比,如此就成了2自由度的机构命题,这样则会比前述以自动控制角度实行的1自由度命题来得复杂且容易犯错。首先在图7基本行星轮系里额外把指向器固连在3(72)齿圈上并套在中央轴外,现假设左右两轮分别输入角速度ωL与ωR,这两个角速度输入经左右定轴轮系再到行星轮系机构,之后会令该指向器输出Ω角速度,这样就有着Ω=ω3的关系式,接下来,我们就能运用传动原理分析其数学关系,以下是其推导过程。
(1) 负号差动机构:从转化机构传动比公式(16),及Z2=24,Z3=72,得如式(17)重整后的公式
(26)
(2) 针对左定轴轮系传动关系:从图6中已知ZL=20,Z4=80,可算得同于式(18)形式的公式
(27)
(3) 针对右轮传动:从图6中已知数齿为20T齿轮对与32T齿轮对,可算得同于式(18)形式的公式
(28)
将前面式(27)与式(28)二项代入到式(26)关系式,重新整理可以得到如同式(21)的数学关系式:
(29)
以机械机构角度进行计算该款指南车角速度特征求出的β补偿因子如式(29)所示,其结果完全与以控制理论计算所得式(25)结论一致,这支持着式(6)所做的假设,真是殊途同归。从机械设计方法的计算所得式(29)中,只要与式(21)逐项一一对应,很容易地就能反推得出控制通道中各项控制环节的比例因子:βCL=4/3,NTL=1/4,βCR=1/3,NTR=1,β=1/3,以及L=3R,这项由机械原理所推算的结果与本节前半段7.1以控制理论角度计算所得到的式(23)、式(22)与式(24)是一模一样。
8 控制理论的推广
回顾指南车的控制理论,由于各种环节都是比例因子,因而可推广至所有线性构件组成的指南车,从这个推论知道,转向机构做为指南车的核心部件并不限于本文分析所用的差动轮系机构,例如《宋史·舆服志》文献记载的吴德仁离合器式指南车、颜志仁绳索传动之差动式指南车[1]、杨衍宗等导螺杆式指南车[15]等,还有宋力斌斜面顶推式指南车[8,9],该项发明的指南车特别精简,完全不使用齿轮,而是使用了斜面、杠杆与曲轴等很原始的简单机械,本节将以图8所示的斜面顶推式指南车进行控制理论的计算,当然是沿前面第4节提出的“输入转一圈”的计算法则,并就所得结果加以推导出该指南车其几何特征该如何设计,才能符合不变性原理。

图8 宋力斌发明的斜面顶推式指南车原部件图
首先来看图8中左轮不动仅右轮转动的运作情况,假设图8中22扁平状滚轮是处于右轮进行顺时旋转的初始位置,它正紧贴着左侧的2302斜面,该斜面是在23套筒(把中央水平轴线穿孔的圆柱经平面斜切并套入2左半轮轴)右侧的斜切平面,所以当右轮顺时转动输入一圈时,扁平状滚轮会在斜面上滚动并绕轮轴转一圈,因此求得右轮传递给该等效控制器的传递因子为NTR=1,接着也让套筒在水平轴方向先向右后向左地往复移动,并通过3小滚轮摇动着5杠杆和6连杆进而带动13曲轴旋转一圈,正好驱动指向器转动一圈,也就是右侧输入等效控制器其补偿因子为βCR=1,这样从左轮不动右轮单侧旋转输入一圈就可以求得控制通道之传递函数的补偿因子为β=βCR×NTR=1×1=1,再将此代入到式(6)得
Ω=βΔω=Δω
(30)
再依指南车控制理论可进行推论,即考虑该补偿因子必须符合不变性原理,则它要等于干扰通道的传递函数GD(s)=R/L,如不考虑负号的话,可算得
(31)
以上依指南车控制理论推导出如何设计该款指南车其轮车架的几何条件,也就是该指南车左右两轮之轮轴间距L必须设计成等于车轮半径R的尺寸;同理,另从右轮不动仅左轮转动也能算出同样结论,这个式(31)由指南车控制理论计算的结果,与该发明专利文件[8]里所陈述的轮轴间距与车轮半径的设计规范是完全一致的。
另有一种构造更简单由李琛发明的指南车[16],它并不是依靠指向器辨别方向,而是经判读两轮相对运动位置从而了解到车头的指向方位。如将指南车分为无转向机构与含转向机构等两类指南车的话,那么李琛的指南车就属于无转向机构指南车或简称无机构指南车,如果按严格指南车五构件要求的话,该指南车缺了指向器与转向机构等重要构件。由于这类指南车没有提供输出指向器转动的转向机构,等于是没有了控制器,那么,本文创建的控制理论也就无从计算了。
9 理想与现实之间的误差
虽然前馈调节控制在理论上可以实现无误差调节,能充分体现不变性原理,可是指南车的实际行驶情况会碰到不可测的干扰,使得车轮自旋与行进轨道并不是完全耦合作用,旋即破坏了式(4)纯滚动行程差恒等关系式,例如,当轮子发生打滑空转现象,导致车轮自旋过快而多增加Δε角速度,使得ΔS′>ΔS,这项多出来的信号会经由控制通道传送出去,进而影响着指向器的转向;又如,当轮子发生腾空跳动现象,导致车轮自旋过慢,使得ΔS′<ΔS,也就相当于车架多弯了Δσ角速度,这项干扰信号会经由干扰通道传送出去,进而影响着指向器的转向,今将前述两种指南车在实际路面行驶时通常会发生的因素纳入指南车控制理论,简单推理,就能够列出车轮自旋与行进轨道不完全耦合作用下的控制系统输出入之数学关系式如下:
(32)
上式中间的前一个互减项因前馈控制系统完全补偿作用得以归零,因此会残留剩下后一个互减项,这就是车轮发生跳空或打滑现象对指向器的转向输出造成影响,又由于这两种现象为独立互斥事件,这些不可测干扰相互之间不生抵消,都会输入到控制系统,进而让指向器衍生累积偏差,而且由控制理论证实了指南车缺乏可以侦测鉴别车轮跳空或打滑扰动的机制,导致这些干扰不可能被量测出来。虽说人是可以判别这种累积偏差,然而机器却是无从知晓,使得有偏差产生但无法被消除。
虽然有偏差产生就无法被消除,然而指南车控制有一种自动重设定特性,例如以指南车启始指向器所指角度为极坐标零度角,且此处对指南车平移运动不做讨论,所以只要一路追踪其旋转运动就行了。思想实验追踪情况如下:指南车刚开始行驶平顺,然后于T1时碰到不可测干扰,此时指向器产生偏差E1角,然后继续纯滚动行驶,这时指向器依然是呈E1角样貌行平移运动,又于T2时碰到不可测干扰,使得指向器产生偏差E2角,因而累积偏差变为(E1+E2)角,后来又恢复纯滚动行驶。仔细检视从T1与T2这一段期间的纯滚动行驶过程,指南车控制系统就好像自动重设定一样,它会遗忘先前的偏差,而是拿先发生的偏差E1角当成最优控制条件的期望值,也就是重新设定了这个偏差角为零度角,因此控制系统在这一段纯滚动期间里仍然实现完全补偿控制,也就是任意行驶并没有对指向器产生偏差,换句话说,指向器自动以新重设后的零度角保持平移运动,因此该控制除了会自动重设定并没有记忆机制,由于这个作用称指南车控制系统具无记忆性自动重设定特质,因此,指南车是不存在有所谓的给定环节[7],所以也就没有设定值以及设定值偏差的问题。
虽然控制系统不具记忆性,但以启始方位角来看,每次所生偏差都会残留而累计下来,又由于指向器圆周旋转之周而复始特性,庇护了长时间行驶之下所累积的超大偏差不发生破表现象,绝对安全没有危险可言,且控制系统仍然依照着转向机构专有特性不断持续控制着,又由于指南车控制系统有着无记忆性自动重设定特质,前馈信息永远是针对当下扰动量进行控制,而不受之前任何扰动包括累积误差的影响,完全不针对被控对象的偏差量进行控制。
这里总结一下,由于指南车除了有制造上的系统误差[17,18]之外,它还无法克服车辆行进间地面颠簸或光滑所产生的误差,总之(1)轮打滑则轮多转,从而导致指向精度更差;(2)车跳动则车多转,从而导致转弯精度更差;(3)现实工艺非线性,从而导致构件精度变差等无法消除的三差环节,导致不可能将近似理想化指南车化为现实,换言之,在现实环境下为指南车进行定量实验是没有实质意义的,这也就是为什么一般指南车设计文献只讨论制造精度而不讨论其定向能力精度的重要因素。
10 常见误区厘清
在进行讨论之前,先来厘清所谓的自动控制。这里举个棒球赛例子,球要投得精准,是投手控球能力的控制问题,这显然是人工控制;至于自动控制,则是相对人工控制概念而言的,指的是在无人直接参与情况下,利用控制装置使被控对象或过程,能够自动地按原先设计或预定规律运行。照这个讲法,指南车的保守指向作用,并不是人工控制,它是靠人们设计在车里头的机关或机构来控制方向的,因此,指南车的确是拥有自动控制系统的机械装置,至于有很多学者认为指南车有定向作用,甚至认定由于差动结构具有负回馈作用,它是反馈控制,真的是这样吗?以下深入探讨。
10.1 指南车其指向器有定向作用,真的是这样吗
指南车能够执行指向功能,并不能做到定向。要赋予定向功能,以控制的观点,不外乎就是要知道自身与外界方位情况,然后设立预定方向,接着做好控制以稳定方向。就此定向要求来探讨,指南车的确是有三大盲点:其一如要达到设定方向目的,得为它先行设定方向以利后续执行调节方向控制,但指南车没有设计输入系统设定值的操作构件或界面机构,它是以启始方向为方向,因此要停车后,如指向器是固连着机构输出件,则要抬高车架转动轮子才能重新给定指向器方向,至于车子行进间是办不到的;其二如要达到稳定方向要求,需要提升追踪精度和抗干扰性,然而在缺乏反馈通路情况下,无法对系统内外干扰因素的总和做出实时估算和相应补偿,指南车设计没有负反馈控制回路,这些要求全做不到;其三如要达到固定方向作用,得知道方向预计设定在哪个方位,换句话说,得量测输出端信息与外界坐标之间的联系才行,可是在指南车里并没有作这样设计考虑。
就以上原因分析,明白看出指南车本身就是做不到定向要求,因为不管方向要怎么定,这所有的基准(固定)、判断(设定)与调整(稳定)都是在人的脑海里进行的。那指南车指向功能到底是什么呢?方向何来呢?由来又是什么?这得先来谈谈指南车所认定的方向。由于指南车始终是以车刚开始行驶的启始方向为指向依归,显然方向成了时间为零的边界条件,而且一直延续到任何时刻都丝毫不受车辆任何转弯的干扰,指向器都得要在静止坐标中始终保持平移运动而无任何旋转运动,如此才能守住启始方向,所示空间方位看起来像保持不变,这就是指南车指向功能的真谛。由此看来,指向作用并不是指南车所能提供的功能,而保守方向才是。当车刚开始行驶时,如果指向器所示启始方向就是我们要指定控制的方向,那么就可以说,指南车拥有保守指向作用。
保守指向作用是我们探讨指南车的主题,其最重要作用关键所在,就是指南车在平面上任意行驶,本身自有能力把指向器旋转与车辆拐弯这两个运动综合起来的偏差始终调节为零,这正是经验公式(2)的物理图像,而一般只知道该经验公式,进而猜想并推断指南车拥有反馈控制机制,然而事实真相又是如何呢?这个空间运动答案将随着选取系统范围不同而有所差异,以下就个别观点与整体观点来探讨相关命题。至于反馈控制机制方面的疑云,后续还会深入探索拨云见日。
首先以指向器做为受控对象来谈,指南车的指向器与车架并不发生耦合作用,事实上指向器并不受车架节制其运动。证明很简单,只要将指南车腾空架高让轮不着地,然后单单旋转车轮时,就只有指向器会随之转动,而车架则纹风不动。这个明显事实指出指向器旋转与车辆拐弯这两个运动,只是单纯以相对反方向运动而已,它们是独立发生的事件,彼此一点关系都没有,只是它们之间的等量反向相对运动,就那么巧,正是由于同时巧合发生,在静止坐标空间上同时合将起来的效果,被认为是保持不变守住方向。因此,能控制指向器保守指向的,也只是个巧合。
如果将指向器与车架统合起来看,意义就不同了,这整体观点会让指向器本身与车架融合成一系统而分不开的,本研究也是居于这个整体观点,虽然实际上,指南车并没有加法构件或机构,能把车架拐弯角速度与指向器旋转角速度这两个加起来之和为零,然而相对于惯性坐标的观察者而言,指南车相当于一个运动坐标系,而指向器则是在这运动坐标系上进行自旋运动,由于指南车如刚体平面运动般可看成是刚体的平动与转动,因此,惯性坐标观察者看到的指向变化是指南车刚体的转动与指向器在此刚体上自旋的叠加状态,整体观点还是能将这两股相对运动视同加法作用,就是一个偏差加上一个补偿,整体系统逻辑上是可以这样看待,宛如双人跳舞般,你来我往、舞步同调、节奏一致、淋漓曼妙。保守指向就这样发生作用,无时无刻无所不在。
10.2 差动结构有负回馈作用,真的是这样吗

图9 杨衍宗等第二款指南车转向机构图
“反馈或负回馈”一词在自动控制领域是个极其重要的概念,乃指将控制系统把信息输送出去,又把其作用结果返送回到输入端并以某种方式改变输入,它们之间存在因果关系的回路,进而影响系统功能的过程。依本文为指南车创建的图3控制方框图来看,显然反馈回路是不存在的;至于机械方面的观点,有文献指出当指南车转弯时,两轮差动将使得负差动的机械机构输出的转向与车子转弯角的方向等量反向,这样就可以实现负反馈[1]。这里将以一个负号差动机构来检验这个说法是否成立,此处选用杨衍宗等设计的第二款指南车[15],它的转向机构与图6谢龙昌等设计例3指南车基本是一样,其实际机构设计如图9所示,都是如图7所示属负号差动机构的基本行星轮系,有着与前述说法所指的负差动特性,另从该文献得知Z1=Z2=Z5=Z6=20,以及Z3=60等个别编号齿轮之齿数信息,那么,从图9中可观察到齿轮2为行星轮、齿轮1为太阳轮、齿轮3为齿圈,这样的输出入件正是第6节的②以齿圈为左侧输入、太阳轮为右侧输入而行星架为输出的组合情况,其中,行星齿轮2是套在行星架4的系杆上。现假设左右两轮分别输入角速度ωL与ωR,且这两个角速度直接传动到行星轮系机构,接下来就能运用传动原理分析其数学关系,以下是其推导过程。
(1) 负号差动机构:从其转化机构传动比公式(16)与Z1=20,Z3=60,得如式(17)重整后的公式
(33)
(2) 左轮传动关系:当左视图9中左轮6顺转时,俯瞰齿轮3会反向逆转,两者反向则传动比取负值,又齿数Z6=20,Z3=60,且ωL=ω6,由此可算得同于式(18)形式的公式
(34)
(3) 右轮传动关系:从图9中左视右轮5顺转时,俯瞰齿轮1会跟着顺转,两者都是正向,因此
ω5=ω1=ωR
(35)
将前面式(34)与式(35)二项代入到式(33)式,重新整理可得到此二进一出差动机构角速度关系式:
(36)
(4) 针对输出系杆:因转向机构输出件上齿轮啮合着同齿数连住指向器的平齿轮,两者等齿反向,得
Ω=-ω4
(37)
将前面式(37)代入到式(36),并经重新整理可以得到如同式(21)的数学关系式:
(38)
这个从机械原理计算所得的式(38),其乃该款形同式(21)的指南车角速度特征公式,只要与式(21)逐项一对一进行各别比对,很容易地就能反推得出控制通道中各项控制环节的比例因子,结果发现有这些:βCL=3/4,NTL=1/3,βCR=1/4,NTR=1,β=1/4,以及L=4R,这些结果完全与本文控制理论所得推理是一致的,真是条条道路通罗马。整体分析之后,接下来将探讨指向器运动细节。
这里沿用第4节控制理论计算法则里采单轮不动仅转动另一轮的作法,例如当右轮不动左轮顺时旋转输入到图9所示的转向机构则车身会逆时旋转运动,此时左轮6顺转为正向且ωR=0,这些代入到式(36)得到ω4为负值,即该转向机构的输出件会受式(36)调控而产生逆转现象,其输出会与车身转弯方向相同,让逆转角度加大,这并不同于前述文献[1]负反馈的说法,该款设计又为了要让指向器能够维持在原方位,只好在转向机构的输出件先不装指向器改安装一个平齿轮,再啮合相同齿数的平齿轮并固连一个转轴使其能安装指向器,这样就同式(37)那样能使指向器与原输出件发生等量反向的角速度,从而力保式(38)的转向功能,显然,负差动输出负反馈[1]的说法完全站不住脚。
或许有人会认为前述例子只是个特例,并不能以偏盖全证明什么!小心求证是对的,那么,这里还可以再举另一种常见的设计,如由卢志明设计的第b款指南车[19],并拿其角速度特征的数学模式来论事,由于版面受限,这里不详列其设计图,欲知详情者敬请参阅该文献。由于该b款的转向机构是采汽车常用的差速器,它也是负差动机构,其输出入角速度数学模式原为Ω=(ωL+ωR)/2,如把差速器当成指南车的转向机构时,最简单做法就是在差速器右侧输入之传递装置中插入安装一个反相器以便进行方向校正,使得输出入角速度关系一下逆转为Ω=(ωL-ωR)/2,这就与前面第4节提过兰开斯特指南车有着相同的数学模式[10],因而使得指向器有着正常作用。这个例子是在转向机构输入件之前进行了方向校正,不同于前一个杨衍宗第二款指南车是在转向机构输出件之后进行方向校正。综观以上这两个例子,充分显示出转向机构并非是促成指向器有指向作用的绝对要素,如还要硬说转向机构的负反馈作用起到了指向功能的话,那就不靠谱了,况且转向机构到底有没有负反馈作用,这还是个大疑问呢,也需要进一步深入探讨才能确认,以下就来讨论这件事。
或许有人会认为前面文献推论负差动机构输出具负反馈作用[1]的说法过于笼统,那么我们接着就来探讨较明确的说法,譬如,也有指南车机械专家认为所谓的“负回馈机构是指南车的主体,指南车因为两轮的速度差而造成车身旋转,负回馈系统则使输出件能够反向消除车身的旋转量,使其回到固定指向的目的”[20],按照机械观点来看,差动轮系是具有负回馈作用,这样描述的确明确多了。如果差动轮系真的存在有负回馈作用,那么这个作用只能是差动轮系的专有特性,又差动轮系内部各个构件的传动比正是该装置的专有特性,而该装置的负回馈作用又是涉及到角速度的议题,那么负回馈作用的数学模式必然会反映在此装置传动比公式的数学模式里,现在就拿差动轮系实际设计案例进行深入探讨有无此事,当然也是基于前面讨论所共通的负号差动机构。

图10 卢志明设计第c款指南车结构示意图
接着就以新案例进行探讨,这里就拿图10卢志明设计的第c款指南车[19]为例,当然也是基于共通的负号差动机构,其输出入件安排正好是第6节的③以齿圈为左侧输入、行星架为右侧输入而太阳轮为输出的组合情况。现为了便于讨论,从图10中左下角左轮开始依啮合次序给定齿轮编号为1至6号,各齿轮齿数详情如图10内容所示,例如齿轮1(左轮)Z1=14T,齿轮2(内齿圈内外均齿)Z2=42T,齿轮4(中心轮)Z4=28T,齿轮5(行星架)Z5=40T,齿轮6(右轮)Z6=8T,每个齿轮组件皆采用ωi代表该i编号齿轮之角速度,其中由编号4之中心太阳轮固连转轴直接输出指向器,驱之产生指向器角速度Ω,因此有着Ω=ω4的关系式。刚刚跳过了最特别的齿轮3(行星轮齿)Z3=7T,其乃差动机构中的行星轮,它是空套在齿轮5行星架上系杆的惰轮,所以该轮既可以自转也可以公转,但不做计算考虑;至于左车轮角速度,显然有着ωL=ω1关系式,同理,右车轮角速度也有着ωR=ω6关系式。接下来,我们就能运用传动原理分析其数学关系,其相关推导过程如下:
(1) 针对负号机构之差动轮系:从行星齿轮转化机构传动比式(16),以及已知Z2=42,Z4=28,Ω=ω4,算得如同式(17)并经重整后的公式
(39)
(2) 针对左轮传动定轴轮系:从图中已知齿数Z1=14,Z2=42,且左视左轮1顺转时俯瞰齿轮2为逆转,两者反向则传动比取负值,又ωL=ω1,可算得同于式(18)形式的公式
(40)
(3) 针对右轮传动定轴轮系:从图中已知齿数Z5=40,Z6=8,且左视右轮5顺转时俯瞰齿轮6为逆转,两者反向则传动比取负值,又ωR=ω6,可算得同于式(18)形式的公式
(41)
将前面式(40)与式(41)二项代入到式(39)关系式,重新整理可以得到如下数学关系:
(42)
以机械机构角度进行该款指南车角速度特征的计算求出β补偿因子如式(42)所示,其结果完全与以自动控制角度计算所得式(12)结论一致,这验证了式(6)假设的正确性,这丝毫不意外。只要式(42)与从机械原理一般推导所得式(21)进行逐项一一对映,很容易地就能反推得出控制通道中各项控制环节的比例因子:βCL=3/2,NTL=1/3,βCR=5/2,NTR=1/5,β=1/2,以及L=2R。正是角速度特征公式(21)让指向器具有补偿作用,其源自于前馈控制,而不是差动轮系具有负回馈作用。
11 本研究为何不考虑指南车的动力学
指南车是只有机械机构而没有动力的车辆,需要借助外力牵引才能运动,例如古时候是用牛马等兽力以寻常步行速度加以牵引,并藉由车轮与地面的摩擦力使车辆与指向器相应运动。当指南车受力运动时,就成了一个动力学的物理系统,理应研究此动力学系统下的运动规律,那为何本研究不考虑指南车的动力学,而仅考虑其运动学呢?理由有下列几点。
(1) 延续机械原理的分析基础。随便查阅任何一本机械手册里有关差动机构的传动比,都会与文献[13]里的记载完全一致,任何一本机械原理专书所定义的传动比,其分析基础无一例外都是以运动学为切入点,而本研究也是居于这个基础。
(2) 如考虑指南车的动力学,则难以找到统一的内在运行规律。有文献[21]指出早在中国古代的指南车中,就已经出现了面齿轮副的雏形,此文献指的正是第4节里的兰开斯特型指南车,而面齿轮副是此款指南车里转向机构的一部分构件。该文献运用动力学分析了面齿轮副设计状态时的动态特性,研究了啮合刚度、啮合间隙、静态传动误差、扭矩波动等因素对面齿轮副动态特性的影响,以及面齿轮副蕴含的非线性动力学响应。举这个面齿轮副动力学研究例子,就知道要为兰开斯特型指南车建立其动力系统的数学模型是多么的庞杂,更何况尚有千百种运用不同机构所设计的指南车,若就动力模型而言,由于不同机构的差异性,只能针对个别款式设计的指南车进行个案研究,如此将难以找到指南车共通的内在运行规律。
(3) 掌握研究对象的重点特征。对一个物理系统进行基础研究时,需去枝蔓留主干地掌握相关物理量,有时还需加上线性化假设,才得以化繁为简点出基本规律,进而以简驭繁描述相同或近似的物理现象。指南车的方向保守作用是建立在纯滚动的基础上,也因此指南车必须慢速运动,否则一切免谈。由于指南车处在慢速运动,里头机械构件的材料是可以保持近似刚体,同时也使得构件传动近似线性化,有了这些条件,使得考虑齿轮及机构传动时,单以运动学观点就足以描述其运动规律。在研究重点上,例如在汽车里的差速器,它是一进二出系统,是作为引擎动力输出的扭力分配装置,则扭力是其研究重点,显然必须考虑动力学,否则失去研究意义;然而如果将差速器拿来当指南车的转向机构,它变成是二进一出系统,而且指南车主要重点是要达到公式(2)车辆转弯角速度与指向器补偿角速度的约束条件。现考虑指南车是保持慢速的运动状态,则可以想成外界提供的动力,刚好能让指南车里头所有机械构件都处于线性化条件下运作,进而完成式(2)的角速度关系式,也就是单单运用基本的机械原理进行指南车内部运作的基础分析是可接受的,换言之,就像第2、3节中针对指南车保守指向作用进行的运动分析与建模那样,无须考虑力的作用,单以运动学观点就足以找到满足经验公式(2)的运动规律,而本研究也证实了这一观点。
12 指南车为何而发明,又有何用
本文所论及的理论公式,以及结构图都仅是古代指南车的实现,这些思维远远超出了古人的能力范围,那它们是怎么办到的呢?古人凭借着勤奋的双手与不知亦能行的朴实智慧,创造出不可思议的指南车发明物,其背景是黄帝与蚩尤进行生死存亡之战为破大雾迷阵的一项发明,是战争“需求”创造了“指南车”发明。人类的发明史其实有不少残酷性,所幸,经军转民用之后,这些发明都有利于社会民生,但现在有了卫星导航,那么指南车还有用吗?
其实需求是有了,例如文献[22]用上指南车并进行机电整合创造出新的服务型机器人或三轮车,可用于没有卫星导航又没能用上循线机器人的方向指引应用场景。其实,指南车最大用途是在教育领域,例如文献[10]用来学习曲面与向量平行移动的概念,或如本研究由于牵涉到控制理论,此一研究成果可用来学习控制学上的一些基本概念,例如第4节所讲的“输入转一圈”的计算法则,其实这应是在特定时间例如每一分钟内转一圈,本质上就是one r.p.m.之意,如站在控制学观点来看,这就相当于“输入一个step信号”,这在初学者来说就是个不小的挑战。如果用指南车进行这方面的演练,经由“做中学”就能大大减低其学习障碍。又比如,在机械理想化线性组件假设条件下,经过齿轮传动是立即响应的,因此指南车所有控制环节的转移函数并没有延迟时间,而且是也只能是比例因子,这其实是控制理论中最简单计算的实务应用例子,真是易教好懂。此外,由于本研究牵涉到跨领域的难点,为了方便提供偏向机械观的论述,笔者在第4节里拿掉了时间因素,给定“输入转一圈”的计算法则,从计算输入与输出角速度或转速的过程,转换成计算输入一圈与输出几圈的控制响应。
13 结论
这里总结本文三款行星轮系建构的指南车设计案例,皆用图4、图7基本行星轮系做为共通的负差动机构,其传动比公式同为式(16),其主要差异在于输出入件的设计选择,分别说明如下:
(1) 谢龙昌设计例3指南车时,以左侧输入为行星架、右侧输入为太阳轮而输出为齿圈。
(2) 杨衍宗设计第二款指南车时,以左侧输入为齿圈、右侧输入为太阳轮而输出为行星架。
(3) 卢志明设计c款指南车时,是以左侧输入为齿圈、右侧输入为行星架而输出为太阳轮。
由于基本行星轮系中做为输出入件就是齿圈、行星支架与太阳轮等三种构件,除开因左右镜射因素重复设计之外,就剩上述三种不同组合情况,而且本文实际设计案例①输出入组合算得式(29)、②输出入组合求得式(38)与③输出入组合导出式(42),皆与第4节控制理论之式(10)、式(12)和第6节机械原理之式(21)吻合,充分检验了机械原理与控制观点所做的共同推论,据此,已经系统性盘查所有关于该负号差动机构设计方案的机械传动特征与控制特性,全面交叉核实了本文控制理论的正确性。
笔者遍查机械设计手册[13]里所有差动机构的传动比,无一例外都是比例系数,即线性特性,将同本文第6节如此这般,皆能按机械原理探讨指南车的特征公式与控制特性那样,推得行补偿作用的指南车角速度特征式(21),以及行尺寸规范的指南车几何特征式(10),因此,本文所创建的控制理论其数学模型都通用。有着比例特性的传动比数学模式,这项机械特性注定了将差动机构当二输入一输出应用时,若以机械设计方法计算出其输出角速度为两输入角速度的函数关系式,再加上符合指南车指向要求而配套的传递装置,那么可以确定,该项一输出二输入函数关系式,必然是形如式(21)那样由本文所创建的指南车控制理论中控制通道相关左右侧校正因子与补偿因子所组成,因此,任何差动机构乃充当了如图3指南车开环前馈控制系统中控制通道的比例控制器。
本文为研究指南车控制理论建立的系统方框图表明,其乃属按扰动补偿原理工作的开环前馈控制自动调节系统,又由于指南车角速度特征公式(21)是线性组合的函数,而且指南车几何特征公式(10)只涉及比值,这些线性特征显然可以推广至所有线性构件建成的指南车设计方案,因其转向机构传动特性之数学模式的角速度比例值会是个常数,而从车轮与转向机构之间配套的传递装置的角速度比例值也会是个常数,进而可藉由机械观点推算出如同式(21)与式(10)的数学模式,当然数学模式本身会说话,说明了角速度特征公式正是能让指向器具有补偿作用的机制描述,而几何特征公式则保证了该作用能起到完全补偿,且这些公式里的比例因子皆属于指南车控制理论中控制通道的各种环节,显然控制通道也是同属于指南车的专有特性,只是与机械观点有着不同观察侧面罢了,这两者虽有着一体两面的面向之别,本身特性却是不变的。又为了进一步检验此项推广立论的正确性,本文已于第8节中针对一辆完全不使用齿轮设计的宋力斌斜面顶推式指南车进行推算,并依指南车控制理论推算出该款指南车的角速度特征式(30)与几何特征式(31)。由于完全不使用齿轮,若改用机械原理计算会不容易看出全貌。
本文研究指南车内在运作机理的规律,至于其外在的运动规律,是在文献[10]中进行探讨,并于该文献关于指南车运动现象的研究中,已用数学严格证明了角速度特征公式直接掌控着指向器与两侧轮之间的运动规律,无论指南车行驶在曲面或平面都成立,反观在设计上要求补偿作用的经验式(2),该文献也证明了该公式只在平面上行得通,它是曲面广义运动方程[10]跟随作用面退化成平面之后自然衍生而导出的结果,显然经验式(2)与指南车内部运作机理完全无关,因为如果此式是指南车的内部机制,应不受外在行驶于曲面的差别影响,然而该式一旦推广行驶在曲面上就行不通了,这充分揭露了式(2)并不是指南车内部运作机理所行的补偿作用,也证实了正如10.1节里所分析的那样,它只是车架转弯角速度与指向器旋转角速度两股相对运动相叠加为零的平面空间巧合现象(曲面就不成立),显然在理论上并不能用该经验公式推论说指南车拥有反馈机制。
爱因斯坦曾说过:不论有多少实验都无法证明我的理论,但只要有一项反例实验就可以推翻它!。此前方方面面推导皆指明指南车并无反馈回路,但如果有人还不接受此立论的话,那么,这里先假设指南车拥有反馈控制作用,现在来检验这项立论是否成立。这里举个反例实验就行了,首先以左视指南车车头之左侧车轮的顺时旋转方向为正向基准,只需要在实际运作上,令轮子一侧停住不转动并且让另一侧车轮原地持续正转打滑,由定性分析可发现,有一侧轮会与指向器之间的传动,犹如齿轮对般是反向旋转的;在车子不动情况下,如两侧轮彼此交换操作情境,则另一侧轮与指向器的传动,就如同在齿轮对中间插入惰轮般成了同向旋转。前者操作轮乃本文控制理论所描述的右轮,而后者操作轮则会是本文描述的左轮,其中,由于右轮与指向器双方呈反向旋转,所以右轮转速在角速度特征式(21)中必须以“-”号呈现,这就是该公式中会有负号的由来,与反馈回路完全无关。上述两种操作情境如采定量分析,那么,指向器会如第4节控制理论里面进行单轮独立转动的计算法则所描述的那样。这里总结一下前述思想实验,一方面,只能看到指向器会随着车轮持续打滑而转动,且车架丝毫不受影响,假如指南车拥有反馈控制回路的话,就应该会对该项系统外在干扰启动反馈机制,显然实验没能观察到这项相应的反馈动作;另一方面,如以整体运作来看,指南车乃属二进一出系统,由于第4节已证实其内部运作具有叠加原理特性,这说明二个输入干扰源在控制过程中并不会互相传递信息,而且系统响应也没有反馈回路。这项实际操作的反例实验,已充分证实指南车根本没有反馈控制回路。至此,可以毫无悬念地说,指南车并不存在所谓的负回馈机构[19,20]、反馈回路闭循环控制[3,23]、homoeostatic machine[5]等诸多令人混淆的观点。

