波浪-地震对海底管道垂直弯曲段力学状态的影响研究*
高凯歌
(中国石化青岛安全工程研究院,山东青岛 266100)
0 前言
海底管道垂直弯曲段(图1)在海洋油气开发中有着非常广泛的应用,同时由于其特殊的构造,使得海洋管道垂直弯曲段容易损伤,进而失效。海底管道垂直弯曲段内有高温高压流体流动,且同时存在随机的波浪荷载和地震波载荷加剧了海洋管道垂直弯曲段的破坏[1-8],因此,研究海洋管道垂直弯曲段受力变化规律对选管和管道几何参数优化、提高经济效益具有重要的意义。
海洋管道垂直弯曲段所承受的荷载有风、浪、流和地震等,其中最重要的是随机波浪和瞬态海流。波浪是由风或者其它自然原因而产生的水体的垂直周期性震荡,其本身是一种不稳定的非均匀流体。对于海洋管道垂直弯曲段在波浪力作用下的振动,国内外学者已进行了几十年的研究,在理论及工程应用上积累了宝贵的经验,研究成果较多[9-13]。闫相祯[14,15]教授通过有限元方法对埋地管道、弯管穿越强震区轴向应力、轴向应变变化进行研究,得到了影响管道轴向应力、应变的影响因素。T.K.Datta, Kalliontzis C.等[16-18]研究了大变形和大转角管道垂直弯曲段在波浪和海流作用下的动力响应,并在非线性弹性的基础上将剪切效应引入到控制方程中,同时得到管道垂直弯曲段的长度,管道垂直弯曲段角度是影响海洋管道垂直弯曲段挠度的主要参数。Kordkheili[19]提出了一种用于分析柔性管道垂直弯曲段的几何非线性有限元公式。Chainarong[20]等针对大柔性管道垂直弯曲段由于大变形引起的几何非线性特征,提出了一种非线性有限元分析方法对大变形柔性管道垂直弯曲段进行了动力分析,虽然更加真实地反映了大变形柔性管道垂直弯曲段的局部运动状态,但由于其自由度较多,计算耗时较长。同时,国内外学者针对海洋管道垂直弯曲段采用能量方法对管道强度的变化规律进行了研究[21-23],但是针对波浪力和地震波荷载共同作用下管道垂直弯曲段应力的变化规律,相关学者研究较少。笔者基于上述研究现状,采用有限元方法对海底管道垂直弯曲段在波浪力和地震波载荷共同作用下的应力变化规律进行了详细的研究,为现场海洋管道垂直弯曲段在考虑地震灾害时的施工、设计提供技术支持。

图1 海洋工程中海管管道垂直弯曲段段示意
1 海底管道经历波浪力计算
对于深水区域,波浪对管道作用力很小,一般不予考虑,但在浅水区,则须考虑波浪力对管道作用的影响。波浪对海底管道的作用如图2所示。其中fd为波浪力水平分力中的拖拽力,fi为波浪力水平分力中的惯性力,fl为波浪力垂直方向上的上升力。
文中引入附加质量的概念,基于文献调研发现,海底管道除了本身所占据的水体外,还需要考虑管道附近水体流速的改变引起的附加质量,即:
fi=CMρπD24∂u∂t
(1)
式中:fi——管道单位长度所受惯性力,N;
D——管道外径,m;
CM——管道周围水惯性力系数,文中取2;
∂u∂t——垂直于管道轴线的水质点相对于管道的加速度,m/s2。
稳定海流工况下速度力可表示为:
fd=ρ2Du2
(2)
式中:fd——管道单位长度上所受的速度力,N/m;
u——垂直于管道轴线的水质点相对于管道的速度,m/s。
当D/L≤0.15时,用莫里森方程计算管道受到的波浪力,表示为:
Fx=0.6ρDu|u|+π2ρD2dudt
(3)
Fz=0.35ρDu2
(4)
式中:Fx——管道单位长度所受水平波浪力,N/m;
Fz——管道单位长度所受垂直方向波浪力,N/m;
ρ——水的密度,kg/m3。
通过公式(3)(4)得到波浪力随时间的变化曲线如图2所示:
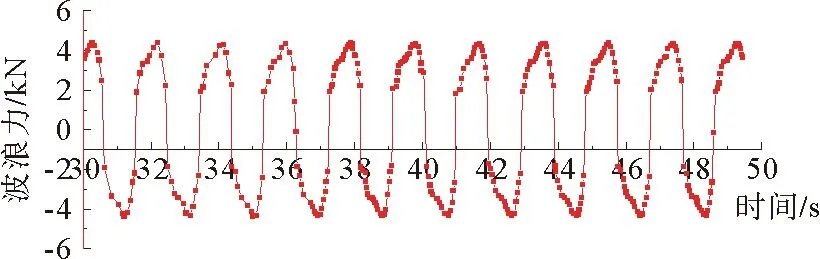
图2 波浪力随时间变化曲线
2 海底管道穿越强震区运动方程研究
将地震波对海底管道的作用效果分为两部分:①v(x,t),地震波作用下管道的横向位移;②u(x,t),地震波作用下管道的轴向位移。则地震波作用下埋地管道二维振动运动方程为:
{ρA∂2v(x,t)∂t2+kl[v(x,t)-gl(x,t)]+EI∂4v(x,t)∂t4=0 横向振动
ρA∂2u(x,t)∂t2+ka[u(x,t)-ga(x,t)]+EI∂2u(x,t)∂t2=0 轴向振动
(5)
式中:A——管道横截面面积,m2;
ρ——管道密度,kg/m3;
EI——管道刚度,MPa;
gl——海洋管道土体横向位移,m;
ga——海洋管道土体轴向位移,m;
kl——海洋管道土体横向弹簧常数;
ka——海洋管道土体轴向弹簧常数。
基于地震波动力学理论海底管道周围土体在地震波作用下的运动波动形状位移函数可以表示为公式(6)所示形式:
(6)
式中:A1——海底管道土体振动振幅,m;
ω——地震波频率,Hz;
λ——地震波波长,m。
通过坐标变换即可求得海底管道最大等效应力,最大轴向应力和最大弯曲应力。本文就管道最大等效应力、最大轴向应力和弯曲应力随剪切波速度、管径、壁厚、弯管角度等因素影响的变化规律开展研究。
3 实例计算及参数研究
采用ANSYS建立海底管道垂直弯曲段有限元模型如图3所示,管道物理力学参数:管道外径813 mm,壁厚22.2 mm,管道等级X65,钢材密度7 850 kg/m3,弹性模量207 GPa,水密度1 025 kg/m3,温度60 ℃,输送介质密度30 kg/m3,管道内压7 MPa,管道垂直弯曲段角度30°。管材参数取GB-50470规定的埋地管道穿越强震区时管道极限拉伸强度和容许轴向应变,如表1所示。以经典天津波为例进行说明,采用控制变量法研究不同参数对算例管道强度的影响规律。
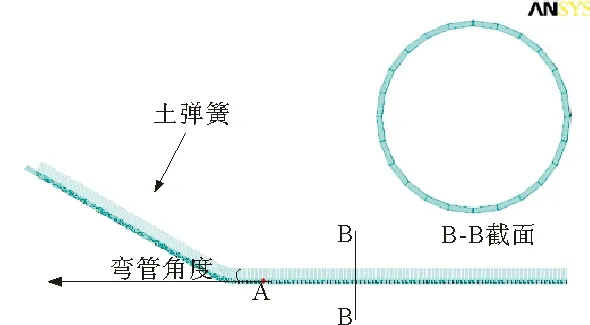
图3 海底管道垂直弯曲段有限元模型

表1 管道许用应变
3.1 剪切波速度对海底管道垂直弯曲段强度的影响
图4所示为海洋管道垂直弯曲段最大应力随地震波剪切波速变化计算结果和规律,可以看出,同一剪切波速下,管道轴向最大应力大于管道最大等效应力,管道应力随着剪切波速度的增加而减小;表2和图5为海洋管道垂直弯曲段最大轴向应变随剪切波速度和地震峰值加速度的变化规律,可以看出,地震波引起的管道轴向应变随着剪切波速减小而增大,随地震峰值加速度增大而增大。
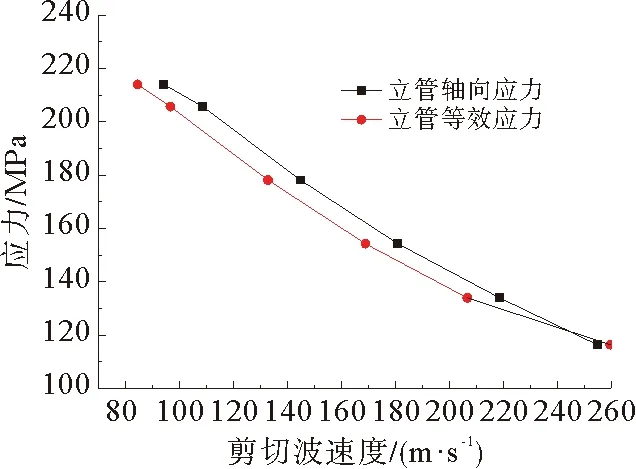
图4 海洋管道垂直弯曲段应力随剪切波速度变化规律
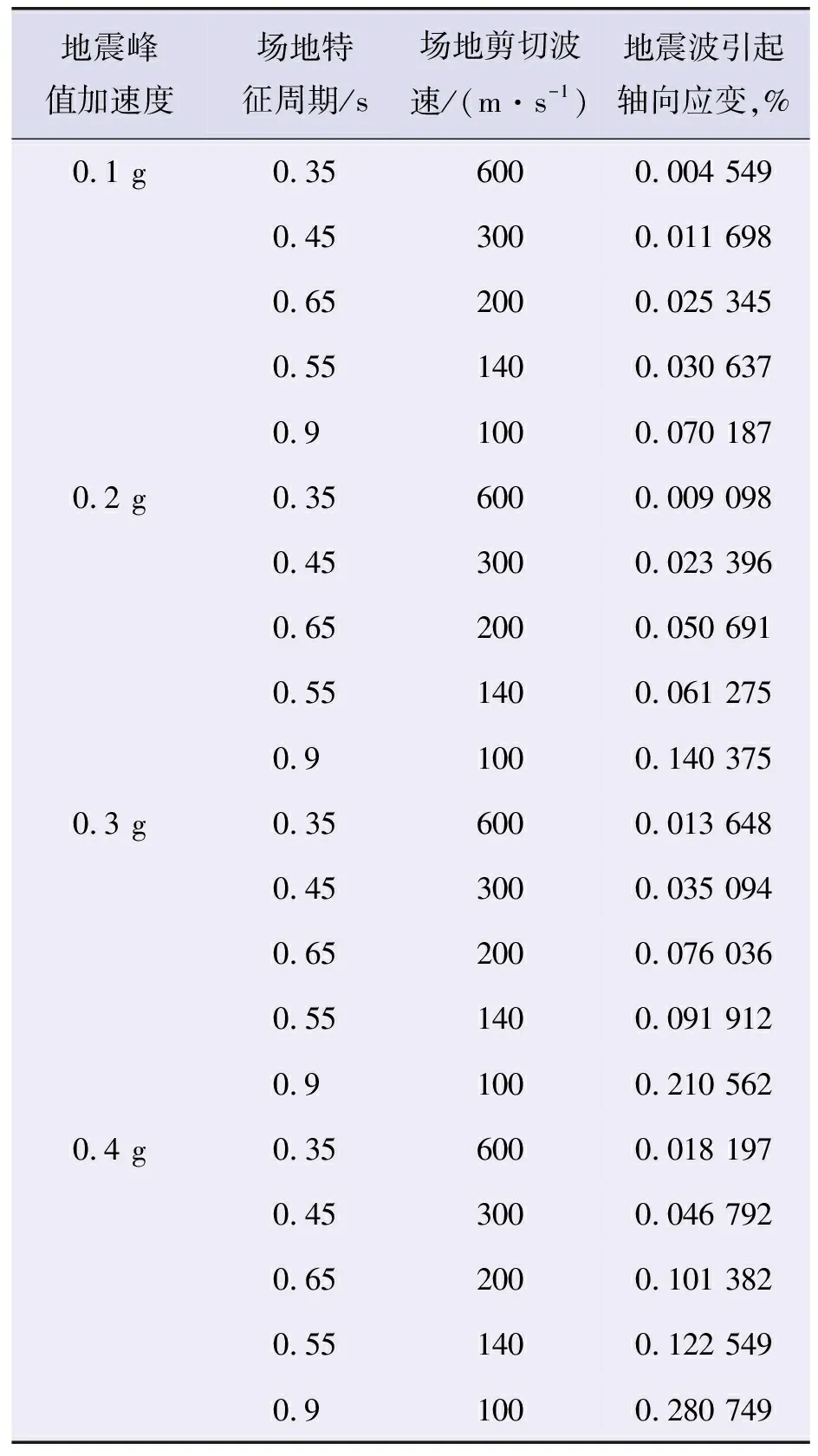
表2 不同剪切波速度下海底管道垂直弯曲段最大轴向拉压应变
3.2 管径对海底管道垂直弯曲段强度的影响
如图6为海洋管道垂直弯曲段应力应变随管径的变化规律,可以看出,海底管道垂直弯曲段的轴向应力、等效应力以及轴向应变随着管道直径的增大而减小,在许可范围内增大管径可以提高海洋管道垂直弯曲段的抗震和承受波浪力载荷性能。
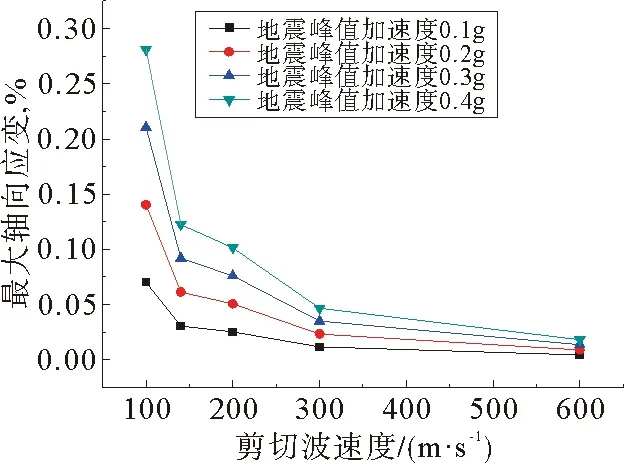
图5 海洋管道垂直弯曲段最大轴向应变随剪切波速度和地震峰值加速度的变化规律
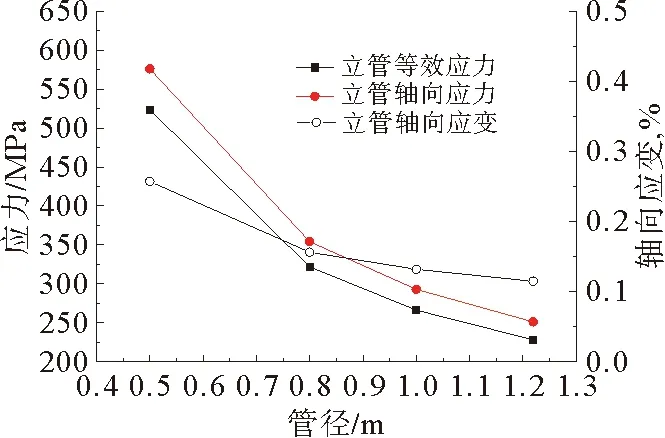
图6 海洋管道垂直弯曲段应力应变随管径变化规律
3.3 管道壁厚对海底管道垂直弯曲段强度的影响
图7为海洋管道垂直弯曲段应力、轴向应变随壁厚变化规律,可以看出,海洋管道垂直弯曲段最大轴向应力、最大等效、最大轴向应变随管道垂直弯曲段壁厚的增加而减小,且管道最大应力出现在弯管下端A(图3)点处。
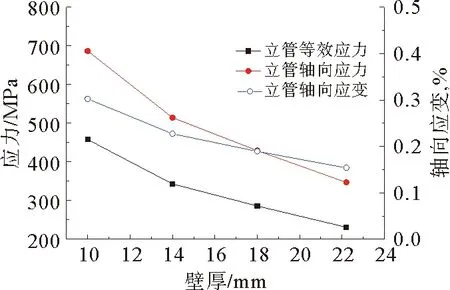
图7 海洋管道垂直弯曲段应力应变随壁厚变化规律
3.4 弯管角度对海底管道管道垂直弯曲段强度的影响
图8为海洋管道垂直弯曲段最大轴向应力、最大等效应力随管道角度的变化规律,可以看出,弯管角度达到30°时,弯管最大等效应力达到了317 MPa,超过了X60的许用应力,考虑到海底输油气管道外侧存在相应保护措施,因此建议海洋管道垂直弯曲段弯管角度小于30°为宜。
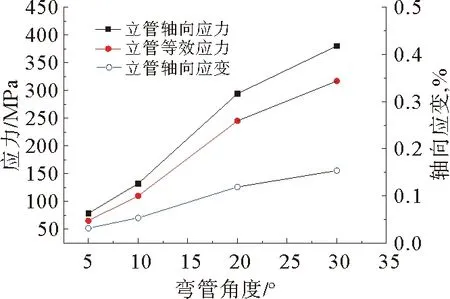
图8 海洋管道垂直弯曲段应力应变随弯管角度变化规律
3.5 海底土体性质对管道垂直弯曲段强度的影响
对陆地埋地管道的研究表明,砂土或粘土的内摩擦角对管道的最大轴向应变和最大轴向应力的影响较明显,通过采用有限元方法对海洋管道垂直弯曲段土体摩擦角变化对管道应力的影响进行研究,如图9所示。结果表明,在波浪力和地震波载荷共同作用下,波浪力对管道垂直弯曲段应力影响相较地震波载荷更为敏感。
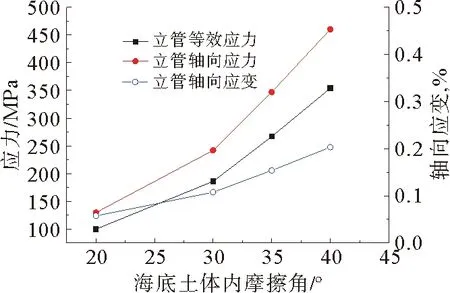
图9 海洋管道垂直弯曲段应力应变随海底土体内摩擦角变化规律
4 结论
a) 在地震波和波浪力共同作用下,海底管道垂直弯曲段最大应力出现在弯管下部A点处,且管道最大轴向应力大于管道Mises应力,都远大于管道垂直弯曲段的弯曲应力。
b) 为了增加海洋管道的抗地震和波浪性能,建议现场使用大直径、大壁厚管道,且管道垂直弯曲段弯管角度不大于30°为宜。
c) 考虑海洋管道垂直弯曲段深埋土体摩擦角特性,波浪力较地震波荷载对管道垂直弯曲段强度影响更加明显。
d) 通过研究管道垂直弯曲段最大轴向应力、最大等效应力、最大轴向应变随管道垂直弯曲段管径、壁厚、弯管角度、土体性质的变化规律,为现场施工、设计提供了一定的技术支持。

