反步法在多输入多输出逆变器系统中的应用

荔凡凡， 董锋斌， 吴 奥， 王锦博

(陕西理工大学 电气工程学院, 陕西 汉中 723000)

电压型逆变器是用于UPS、新能源发电等领域的主要电力电子变换器，其电路本质是一类时变的、耦合的、多输入多输出(MIMO)的非线性系统，采用线性控制规律对其控制具有一定的局限性，因此，将非线性控制方法应用到电力电子装置中来弥补线性控制方法的不足，成为了当前电力电子领域的研究热点[1]。现有逆变器控制技术包括双闭环、无差拍、滑模变结构控制等，虽然在一定程度上提高了逆变器的性能，但也都存在一些问题[2]。文献[3]中以单相电压型逆变器为例，比较了双闭环、滑模变结构以及反步法控制的性能，可以清楚地看到在系统负载突变以及外加干扰的情况下，反步法控制具有明显的优越性。反步法(Backstepping)是一种分若干步来实现控制器的设计方法，通过在每一个步骤中选择虚拟控制量以及构造Lyapunov函数，使其控制效果达到一定的目标，最终通过层层修正，使整个控制器达到理想的控制效果。这种控制方法具有严格的参数反馈，在工业设计中已被广泛应用于非线性系统的控制[4-6]。

基于以上原因，本文将反步法推广到多输入多输出逆变器系统中[7]，以非线性系统三相电压型逆变器为例，选取合适的虚拟变量以及构造Lyapunov函数，设计一个全局渐进稳定的控制器，来得到其反步法控制模型。

1 多输入多输出系统的反步法设计基本步骤

具有严格参数反馈形式的多输入多输出非线性系统的一般表达式为[8]

(1)

式中xi(i=1,2,…,n)为系统的状态变量，u∈Rm为系统的输入变量，y∈Rm为系统的输出变量，Fi(i=1,2,…,n)为光滑函数，Gi≠0(i=1,2,…,n)，且该方阵可逆。

对于满足严格反馈控制结构的系统，基本思想是将系统分解为低阶子系统，并通过Lyapunov函数和中间虚拟控制量的反向递归设计来完成整个控制器的设计。由式(1)可知，系统的阶数为n，因此整个设计可分为n步。

第1步，设计虚拟控制相量x2ref。

根据系统主要输出相量，定义跟踪误差相量矩阵E1为

E1=yref-y，

(2)

式中yref为输出期望值，对式(2)进行求导并整理后得到：

(3)

定义辅助误差相量E2矩阵函数为

E2=x2ref-x2，

(4)

式中x2ref为虚拟控制相量。将式(4)代入式(3)中可得

(5)

根据误差系统，设计虚拟控制相量x2ref为

(6)

式中k1为反馈增益对角矩阵，对角线上元素属于R+，且G1(x1)为非奇异方阵。

将式(6)代入式(5)得到

(7)

对于方程(7)，如果E2→0，则E1→0。

选取Lyapunov函数为

(8)

对式(8)进行求导可以得到

(9)

由于k1为对角阵，且E1、E2为列矩阵，式(9)可以简化为

(10)

第2步，设计虚拟控制相量x3ref。

对式(4)求导得到

(11)

定义辅助误差相量E3矩阵函数为

E3=x3ref-x3,

(12)

式中x3ref为虚拟控制相量。将式(12)代入式(11)得到

(13)

同理可设计虚拟控制相量x3ref为

(14)

式中k2为反馈增益对角矩阵，对角线上元素属于R+，且G2(x1,x2)为非奇异方阵。

将式(14)代入式(13)得到

(15)

选取Lyapunov函数为

(16)

对式(16)求导得到

(17)

由于k2为对角阵，且E1、E2、E3为列矩阵，式(17)可简化为

(18)

这样，就可以获得虚拟控制相量的设计步骤。

第i步，设计虚拟控制相量x(i+1)ref。

按照前面的思路定义辅助误差相量Ei+1矩阵函数为

Ei+1=x(i+1)ref-xi+1,

(19)

式中x(i+1)ref为虚拟控制相量。同理有

(20)

同理可设计虚拟控制相量x(i+1)ref为

(21)

式中ki为反馈增益对角矩阵，对角线上元素属于R+。

选取Lyapunov函数为

(22)

对式(22)求导可得到

(23)

第n步，设计控制相量u。

由前面讨论知

(24)

根据式(24)，设计控制相量u为

(25)

式中kn为反馈增益对角矩阵，对角线上元素属于R+。

将式(25)代入式(24)得到

(26)

选取Lyapunov函数为

(27)

对式(27)求导得到

(28)

式中ki是一个反馈增益对角矩阵，并且对角线上元素属于R+。因此Lyapunov函数的导数为负，则系统是渐近稳定的。

2 三相电压型逆变器反步法控制

三相电压型逆变器是一类多输入多输出非线性系统，逆变器电路连接如图1所示，图中Lf、Cf分别为滤波电感和滤波电容，三相对称负载其性质有阻性、阻感性、阻容性等，本文以阻性负载为例进行控制器设计，负载记为R0。Skj为电力电子开关，其中下标k∈{a,b,c}，j∈{p,n}。

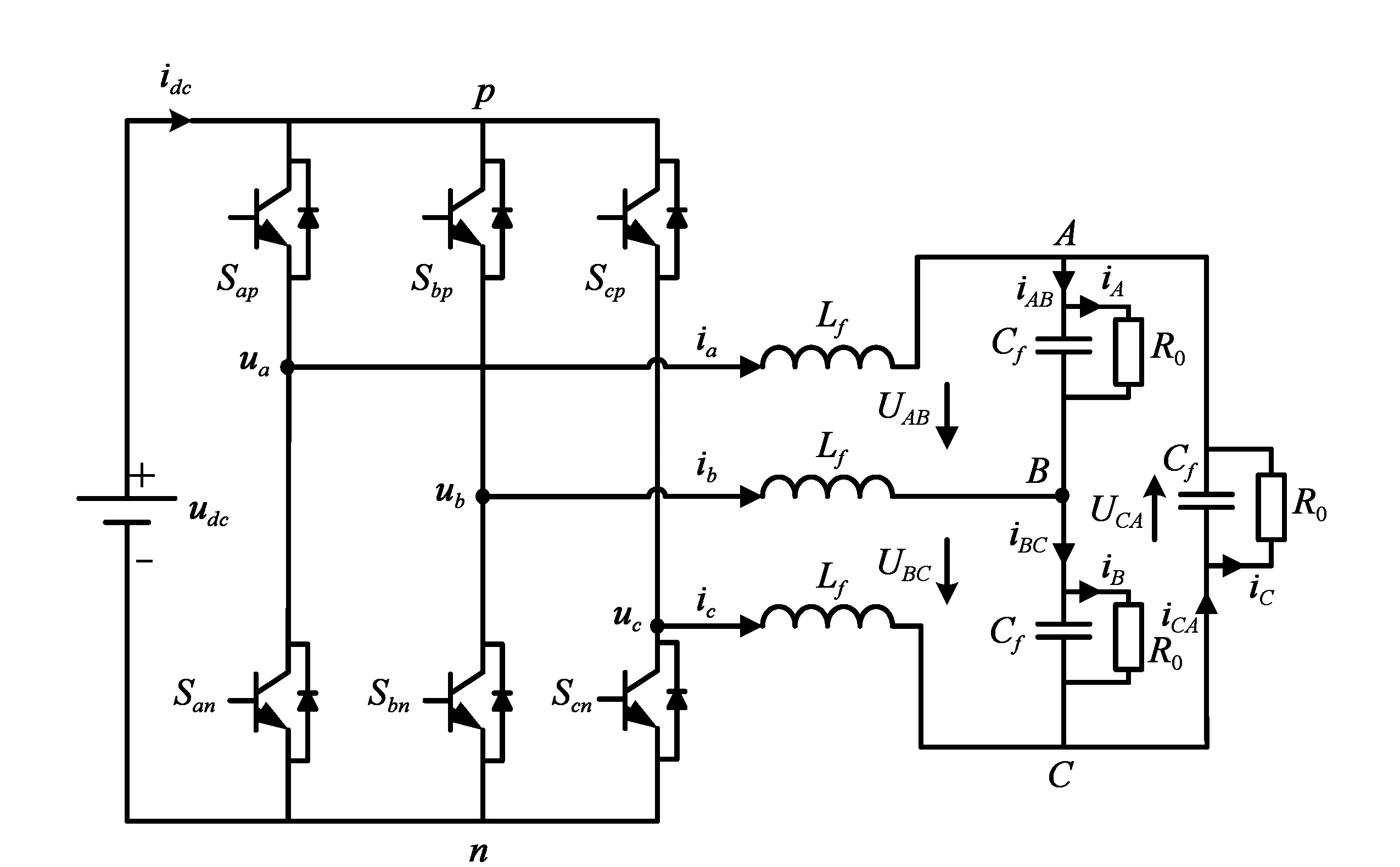
图1 三相电压型逆变器带阻性负载拓扑

在不考虑滤波器中电容、电感内阻以及忽略开关导通的压降和死区大小的情况下，建立线开关函数

Sab=Sa-Sb，Sbc=Sb-Sc，Sca=Sc-Sa，

定义线电流

iab=ia-ib，ibc=ib-ic，ica=ic-ia，

根据逆变器的开关状态及基尔霍夫定律可得

(29)

(30)

式中dab、dbc、dca为线间占空比,dab=da-db，dbc=db-dc，dca=dc-da。

从逆变器系统的数学模型可以看出，式(30)具有严格的参数反馈形式，同时也是一个三输入三输出系统，满足式(1)的统一表达式，因此有

(31)

其中

将各矩阵代入式(2)、(4)、(6)、(14)可以得到

(32)

其中u为所求反馈控制向量。

3 实验验证

3.1 实验参数

为验证在三相逆变器中反步法控制的合理性，搭建实验平台进行验证。实验采用的控制器为德州仪器生产的TMS320F2812型号DSP，所用功率器件IGBT为西门康公司生产的SKM50GB123D。电压和电流传感器采用北京森社公司生产的CHV-25P/200和CHB-25NP型霍尔传感器。

实验主电路见图1，实验参数如表1所示。在控制过程中，通过检测负载的电压和电流在线计算参数R0的大小。

表1 实验参数

反馈增益矩阵中增益系数的选择对系统的动态性能有很大的影响。增益系数偏大时，系统容易振荡；增益系数偏小时，系统响应速度慢。这里反馈增益选为k11=k12=k13=2000，k21=k22=k23=4000。

3.2 实验波形

3.2.1 起动响应波形

图2展示了输出电压和电感电流的起动实验波形。从实验波形来看，起动过渡时间约为8 ms。起动输出电压基本上没有超调。在系统达到稳定状态之后，输出波形将变得平滑且谐波更少，稳定后的输出电压为100 V，输出频率为50 Hz，服从给定基本无静差。

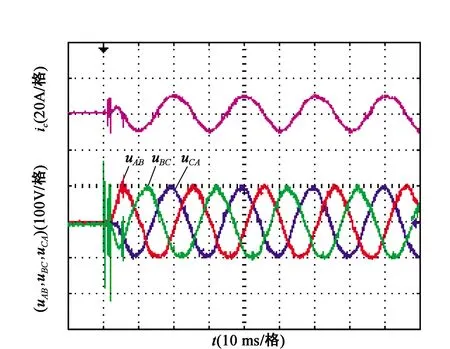
图2 输出电压与电感电流起动响应实验波形

3.2.2 负载扰动实验波形

在负载扰动实验中，电阻先由20 Ω突降为10 Ω之后再增加到20 Ω。从图3中可以看到在负载发生变化后系统的输出电压有很小的波动并且在2 ms中恢复稳定，基本服从给定无静差，而传统的双闭环控制在相对理想的仿真环境下调节时间为2.5 ms[10]，通过对比说明反步法控制策略的抗负载扰动能力强于传统的双闭环控制策略。

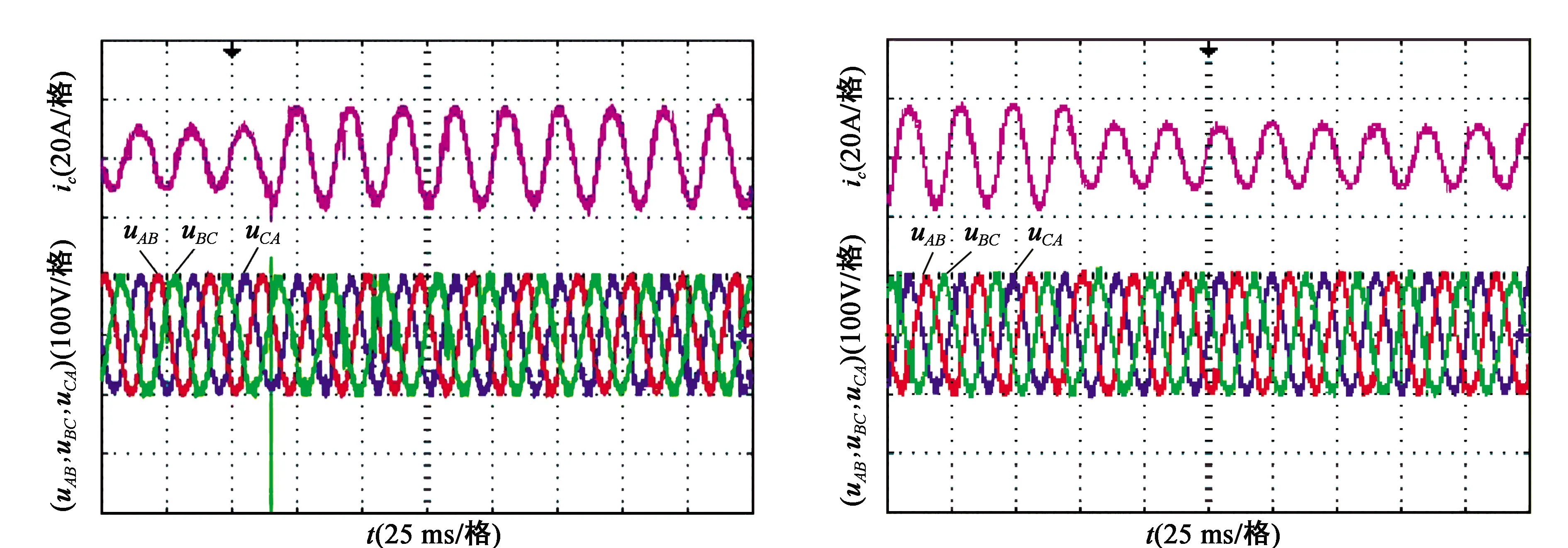
(a)负载突增时响应波形 (b)负载突卸时响应波形

3.2.3 直流电压扰动实验波形

直流电压扰动实验波形如图4所示，分为直流激励先增后减和先减后增两部分进行实验，电压变化为150 V→180 V→150 V和150 V→120 V→150 V。从实验波形可以看出，当给定直流激励发生变化时，输出电压基本不变，即整个系统对直流激励波动有很强的抵抗能力。从式(32)可知，控制器中有对直流侧电压的前馈控制作用。三相PWM型电压逆变器本质为降压型逆变器，在线性区满足uomax=0.866udc的关系，因此对于期望幅值100 V、频率50 Hz的输出电压，当给定直流激励大于等于117.5 V时，其电流和电压的输出基本不变[11]。

同时如果三相电压型逆变器直流侧电压是交流电源通过不控二极管整流经大电容滤波而得到的，反步控制策略对直流激励的前馈作用可以使得直流滤波电容减小，从而使整个逆变器体积相对减小。

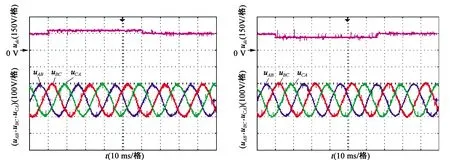
(a)直流电压先增后减波动时响应波形 (b)直流电压先减后增波动时响应波形

整个实验结果表明，在采用了反馈控制策略之后，系统的输出电压、频率服从给定且基本无静差，同时对负载扰动和直流激励的扰动有很好的抵抗能力，相对于传统的双闭环控制策略有明显的优势，说明了反步控制策略在三相电压型逆变器应用的合理性。

4 结论

本文讨论了多输入多输出系统的反步控制策略的设计步骤，并将此方法应用到三相电压型逆变器非线性系统中去，通过选择合适的虚拟控制量并逐步构建Lyapunov函数，使系统中所选状态变量具有适当的渐近特性，最终实现在大扰动下系统的全局渐近稳定性，得到了反步控制策略的一般表达式，最后建立了闭环控制系统实验平台，验证了该控制策略的合理性。