基于Seislet分数阶阈值算法约束的平面波最小二乘逆时偏移
黄建平, 张入化, 国运东, 雍 鹏, 李 闯
(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580;2.西安交通大学电子信息工程学院,陕西西安 710000)
近年来,油气勘探的地质目标越来越精细化,对勘探、开发的要求进一步提高,发展更加精确的偏移成像技术成为必然趋势[1-2]。基于反演思想的最小二乘偏移(LSM)和最小二乘逆时偏移(LSRTM)虽然具有高精度保幅成像的特点,但计算量较大。多炮编码策略如相位编码、振幅编码、极性编码、平面波编码等[3-9]能一定程度提高计算效率,但多炮数据混叠也会引入串扰噪声。李闯等[10]将随机最优化相位编码引入多炮编码中进一步减少了串扰噪声。PLSRTM也可以通过叠加不同射线参数的平面波成像结果来压制串扰噪声[11-12],但平面波道集数量增加会增大计算量。Xue等[13]在目标函数后加上了整形正则化约束项,能一定程度地改善多震源数据的成像质量。Li等[14]则将奇异谱值分析(SSA)引入到PLSRTM中作为正则化约束。除此之外,根据地震数据在曲波域稀疏分布的特点,Herrmann等[15]将曲波变换用作偏移的预处理。相较于来自图像算法的曲波变换,Seislet变换更加适用于地震数据,Xue[16]首先将Seislet约束用于全波形反演中,Dutta[17]将Seislet变换引入最小二乘逆时偏移中,有效地提高了成像质量。在前人研究的基础上,笔者利用Riemann-Liouville分数阶积分理论推导得到分数阶阈值函数,并与Seislet变换相结合得到Seislet分数阶阈值算法,再将其作为稀疏约束算子,实现Seislet分数阶阈值算法约束的平面波最小二乘逆时偏移。
1 方法原理
1.1 平面波编码
多炮编码的方式主要有相位编码、振幅编码、平面波编码等方式。在二维地震数据中对共接收点道集(CRP)进行平面波编码。
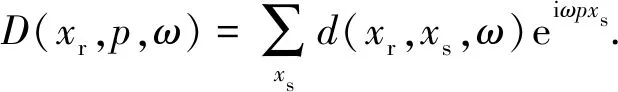
(1)
式中,d(xr,xs,ω)为共接收点道集,由位于横坐标xs处的震源产生,再被横坐标位于xr处的检波点所接收的记录;eiωpxs为代表时间域的时移量,ω为角频率,而最主要的时移参数则是pxs,p为射线参数,p=sinθ/v,θ为地层倾角,v为地层速度。等式(1)主要是将道集中参与时移的道叠加在一起,形成一个平面波道集。
平面波编码的关键是射线参数的选择,最大射线参数pmax应该满足不等式

(2)
式中,fmax为最大频率;Δxs为炮间隔。射线参数的间隔Δp应满足

(3)
式中,θ1为最小倾角;θ2为最大倾角;Np为平面波道集的数量。射线参数p不同,角度范围便不同,照明的区域便存在差异,增加平面波道集的数量能够加强对地下复杂区域的有效照明。但过多的平面波道集也会增大计算量,降低计算效率。
1.2 平面波编码最小二乘逆时偏移
正演的方式主要分为有限差分正演和Born线性正演。其中Born线性正演过程可以表示为
d=Lm.
(4)
式中,L为Born线性正演算子;d为观测数据;m为反射系数。
偏移过程则可以表达为
mmig=LHd.
(5)
式中,mmig为偏移结果;H为共轭转置;LH为偏移算子,在本文中为逆时偏移算子[18]。
假设有n个平面波道集,则反射系数模型M可表示为
M=[m1,m2,m3,…,mn]T.
(6)
式中,mn为第n个平面波道集所对应的偏移成像结果。平面波道集D可以表示为
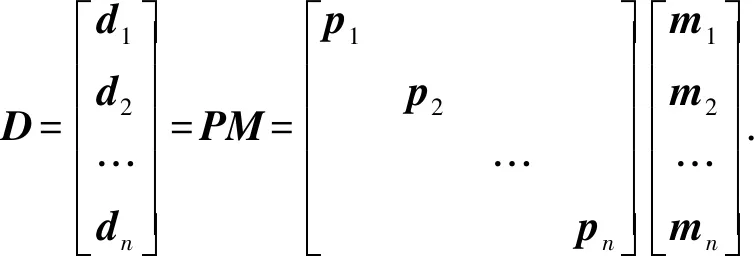
(7)
式中,pi为平面波的Born正演算子。
平面波最小二乘逆时偏移的误差函数可以定义为

(8)
其中误差函数的梯度解为
(9)
其中
1.3 约束的平面波最小二乘逆时偏移
模型M的更新等式为
M(i+1)=M(i)+α(i)z(i),
(10)
z(i)=-f(M)(i)+β(i)z(i-1).
(11)
式中,i为第i次迭代;α(i)为搜索步长;z(i)为共轭梯度;β(i)为共轭梯度修正因子。一个n维函数的共轭方向最多只有n个,大于n次迭代时共轭梯度的计算将失效[19]。为避免迭代误差的积累,本文中在连续计算4次共轭梯度后将使用一次最速下降算法再重新使用共轭梯度法。
对模型的更新等式(10)加上约束得
M(i+1)=S-1TS(M(i)+α(i)z(i)).
(12)
式中,S为Seislet正变换;S-1为Seislet反变换;T为阈值函数,本文中T为分数阶阈值函数。约束算子S-1TS的目的主要在于消除偏移假象和因编码时炮数据混叠产生的串扰噪声。
如果将某个稀疏变换作为一个整体的算子,那么等式(12)就等同于用线性Bregman迭代法使得下列的正则化目标函数最小化[20]。
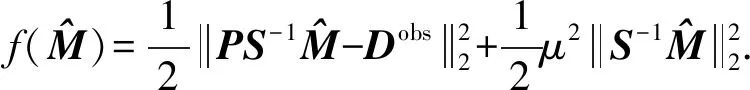
(13)
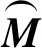
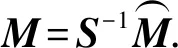
(14)
Seislet分数阶阈值算法约束的PLSRTM流程如图1,其中对初始模型M(0)赋零值。
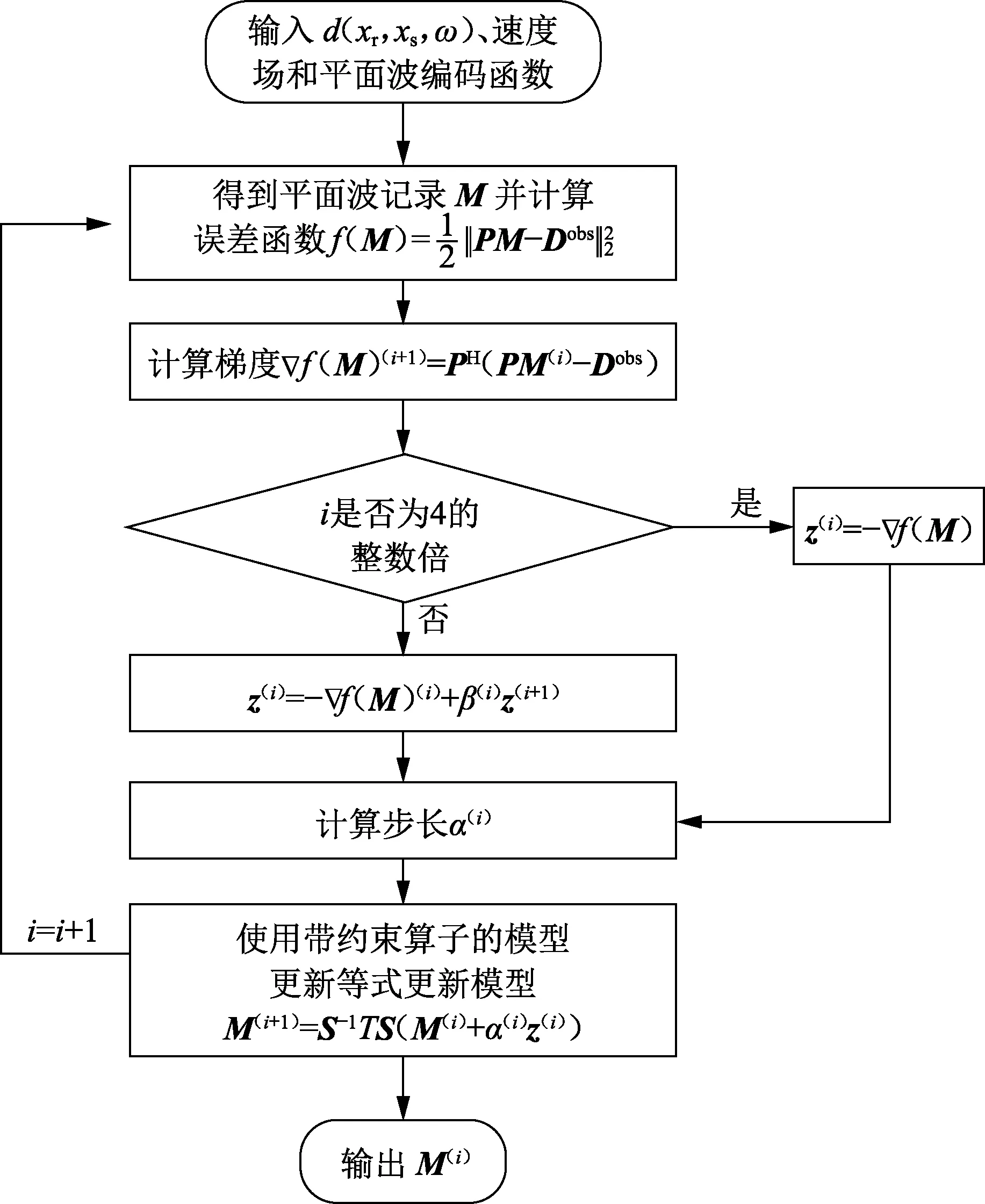
图1 Seislet分数阶阈值算法约束的PLSRTM流程Fig.1 Workflow of PLSRTM with Seislet fractional threshold algorithm constraint
1.4 分数阶阈值函数
传统的阈值函数主要有硬阈值函数和软阈值函数[21-22]。硬阈值函数在阈值附近存在断点,重构信号会产生伪吉布斯现象,一般用得比较少。常用的主要是软阈值函数,但软阈值函数处理后的系数与原系数相比有恒定的偏差,偏差在数值上等于阈值,这会使得重构信号与原信号之间产生较大的误差。有学者也提出过半软阈值,就是在硬阈值函数和软阈值函数中加了一个权系数[23],但这个权系数需根据不同的数据测试后再确定,且与真实系数的相比仍存在一定偏差。

(15)
式中,s为Seislet稀疏变换后的系数;λ为阈值。
设阈值为2,软阈值函数如图2所示,经过软阈值函数处理后的系数与原系数之间存在偏差。
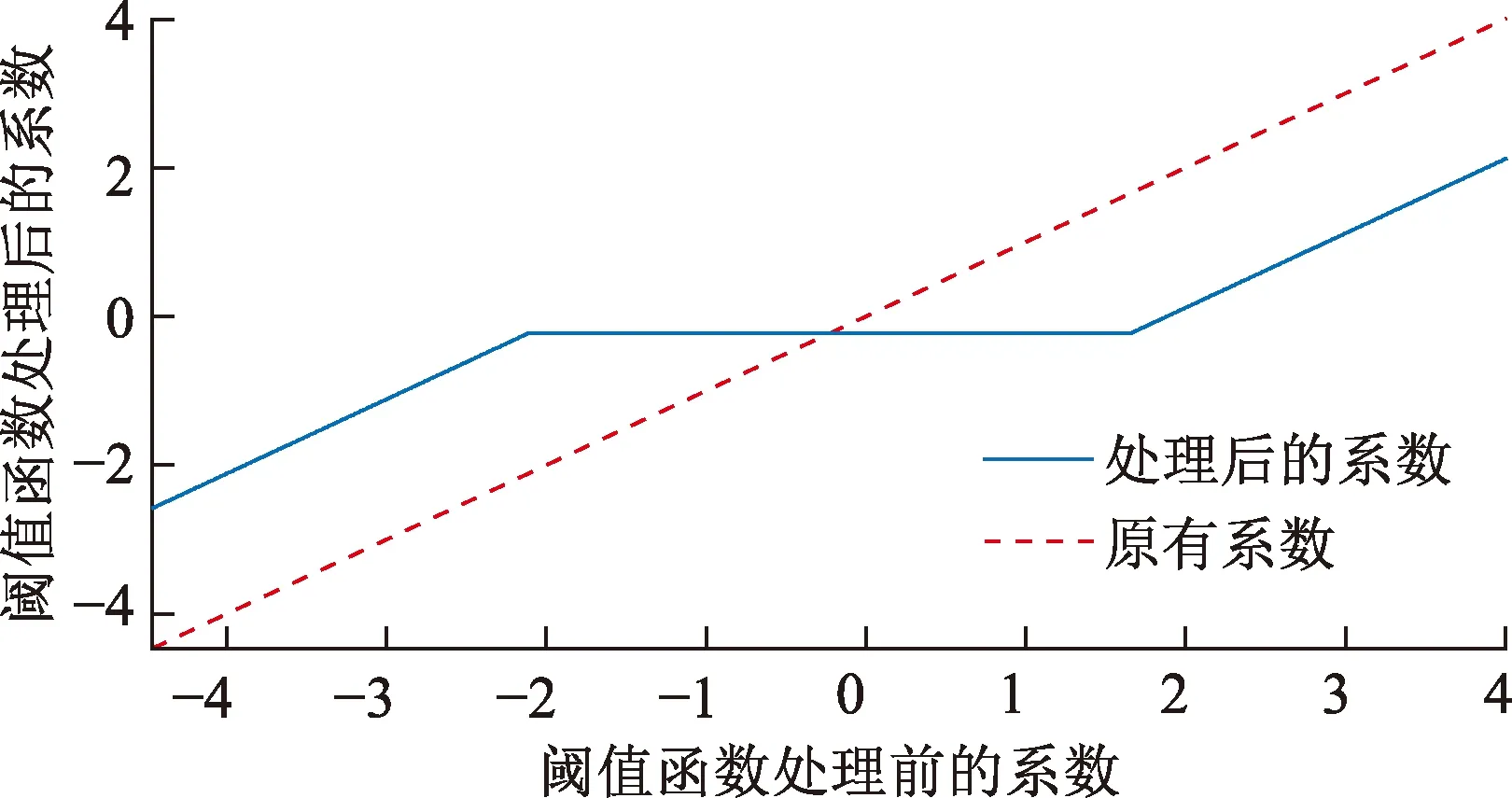
图2 软阈值函数图Fig.2 Soft threshold function
分数阶阈值函数应用了分数阶微积分理论(Riemann-Liouville分数阶积分公式)[24],用该分数阶积分公式对函数进行积分处理积分后,能够增强函数的连续性且保留原函数特征。
本文中提出的分数阶阈值函数如下:
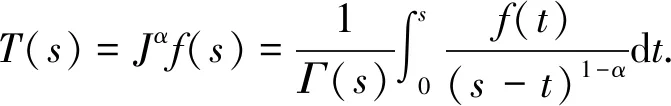
(16)


图3 分数阶阈值函数图Fig.3 Fractional threshold function
由图3可见,分数阶阈值函数在系数偏差上得到了很好的控制,端点处也得到了一定的平滑。
2 Seislet变换测试
常见的稀疏变换有Fourier变换、小波变换、曲波变换、Seislet变换等。其中Seislet变换是专门针对地震数据的一种信号变换,能将数据变换到Seislet域[25],但在进行Seislet变换前需要采用平面波解构滤波器(PWD)对地震数据进行局部倾角估计。Seislet变换需要局部倾角数据作为输入,再沿着倾角方向对地震数据作Seislet变换。Fourier变换、小波变换、曲波变换等均以采样点为变换的单位,而Seislet变换则是以地震道为单位进行变换。
选择某一复杂模型作Seislet变换测试和小波变换测试,该模型数据的横向长度为5 120 m,纵向长度为1 500 m,道数为512,纵向采样点数为150,间距均为10 m。首先对复杂模型分别进行Seislet变换和小波变换,得到对应的系数,再通过选取同样百分比的Seislet系数和小波系数进行反变换得到重构模型,再进行对比分析。
图4(a)所示为某一复杂模型的真实反射系数,再对其进行Seislet变换,得到Seislet系数(图4(b))。由图4(b)可知,Seislet系数主要集中在尺度小于50的位置,且整体分布较为集中。随后分别将Seislet变换和小波变换的系数经过从大到小排序后,选取前1%的系数得到重构后的结果(图4(c)、(d)),前者基本重构了真实反射系数的轮廓,但却没有重构出绕射点(图4(c)),而后者的右侧反射系数很杂乱没有得到有效重构,但能重构下部绕射点(图4(d))。图4(e)、(f)则是分别将Seislet变换和小波变换的系数经过从大到小排序后,选取前7%的系数进行重构后的结果,前者基本与真实反射系数一致,而后者中部断层处的反射系数仍比较模糊。
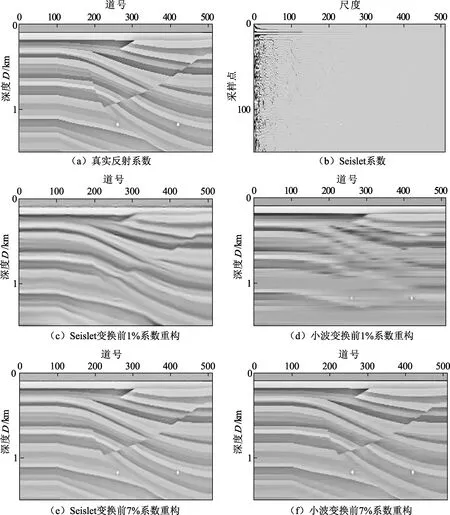
图4 Seislet变换测试Fig.4 Seislet transform test
将同样阈值截取的数据投影到原有的尺度矩阵中(横坐标为尺度)。图5(a)、(b)是分别将Seislet变换和小波变换的系数经过从大到小排序后,选取前1%的系数投影到尺度矩阵的结果,其中黑色数据为前1%的系数。从图5 (a)中可以看出系数主要集中在尺度小于15的位置且分布较为集中, 图5 (b)中的系数主要在尺度小于50且分布相对图5 (a)较为分散。同理,再选取前7%的系数投影到原来的尺度矩阵(图5(c)、(d)),黑色数据为前7%的系数。从图5(c)中得知系数主要集中在尺度小于100的位置,在尺度小于256的范围都有一定分布;由图5 (d),可以发现系数在全局范围内都有分布,且分布较为分散。
最终,可知Seislet变换比小波变换能够更好地压缩地震数据,更能表示地震数据的稀疏性。
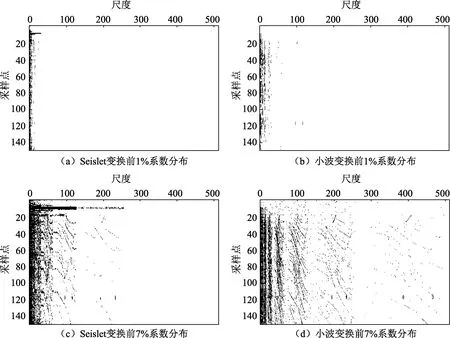
图5 系数在原来尺度矩阵的分布Fig.5 Distribution of coefficients in original scale matrices
3 数值测试
3.1 简单模型测试
选择一个4层的层状模型进行测试。该模型的尺寸为1 500 m×5 120 m,横向采样点数为512,纵向采样点数为150,横纵向采样点距均为10 m。共激发120炮,炮间隔为40 m,检波点为512个,检波点距10 m,最大采样时间为8 000 ms,震源子波采用雷克子波,震源主频率为20 Hz。先使用时间2阶,空间8阶的有限差分算法及PML边界条件进行正演模拟[26-27]得到单炮记录,再用平面波静态编码技术将多炮数据合成具有不同射线参数的平面波道集。
图6(a)为4层水平模型,第一层速度为1 600 m/s,第二层速度为1 900 m/s,第三层速度为2 300 m/s,第四层速度为2 600 m/s,模型长度为5 120 m,深度为1 500 m,图6(b)为偏移速度场。根据公式(1)合成了不同平面波射线参数p的平面波道集,p的取值范围为-0.3~0.3 ms/m,且呈线性变化,共计11个平面波道集。
图7(a)、(c)、(e)分别为简单层状模型经过平面波最小二乘逆时偏移迭代5、10、25次的结果。可以看出图7(a)、(c)、(e)都有不同程度的串扰噪音和少量采集脚印,但图7 (c)的噪音明显小于图7 (a),图7 (e)的噪音也小于图7 (c),这是因为最小二乘逆时偏移本身随着迭代次数的增加能够一定程度地压制噪音。
图7(b)、(d)、(f)分别为PLSRTM迭代5、10、25次结果对应的局部倾角估计。根据颜色条,颜色越深倾角越大,且经过测试发现层状模型本身的倾角值为0,表示为最浅的颜色。由图7(b)、(d)、(f)可知,随着迭代次数增加,局部倾角估计图中颜色团的颜色逐渐变浅,而对应偏移结果的串扰噪音逐渐减弱(图7(a)、(c)、(e))。因此层状模型偏移结果中的非零局部倾角值是由噪音引起的。

图6 层状模型速度场和偏移速度场Fig.6 Velocity field of layered model and migration velocity field
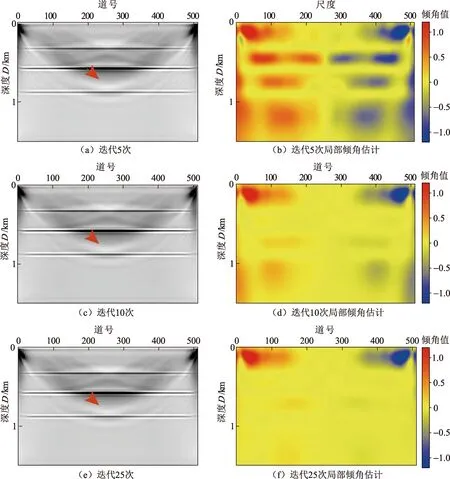
图7 层状模型PLSRTM结果及其局部倾角估计Fig.7 The PLSRTM result of layered model and its local dip estimation
图8(a)为简单层状模型经Seislet分数阶阈值函数约束的PLSRTM迭代10次后的结果,图8(b)为简单层状模型经Seislet软阈值函数约束的PLSRTM迭代10次后的结果,图8(a)、(b)都一定程度上压制了噪音,但前者的压制效果更好,见图中的红圈部分。图8(c)、(d)分别为图8(a)、(b)所对应的局部倾角估计。图8(c)和图8(d)相比,不同颜色的颜色团几乎消失,大部分为局部倾角值为0的颜色,则表明经过Seislet分数阶阈值函数约束和软阈值函数约束的PLSRTM都能够压制串扰噪音和采集脚印。但图8(d)在上部还存在的颜色团较大,而图8(c)在上部附近颜色团稍小,因此经Seislet分数阶阈值函数约束PLSRTM的效果优于经Seislet软阈值函数约束PLSRTM。
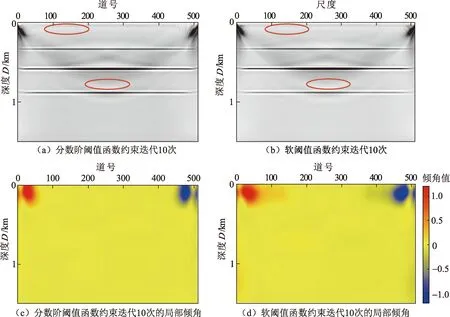
图8 层状模型下不同Seislet阈值算法约束的PLSRTM及其局部倾角估计对比Fig.8 Comparison of PLSRTM with different Seislet threshold function constraints and comparison of dip estimation in layered model
3.2 复杂模型测试
为进一步验证本文方法的可行性,选用某一复杂模型进行成像测试。该模型尺寸为1 500 m×5 120 m,横向采样点数为512,纵向采样点数为150,横纵向采样点距均为10 m。共激发120炮,炮间隔为40 m,检波点为512个,检波点距为10 m,最大采样时间为8 000 ms,震源采用雷克子波,震源主频率为20 Hz。
先使用时间2阶,空间8阶的有限差分算法及PML边界条件进行正演模拟得到单炮记录,再使用平面波静态编码技术将多炮数据合成具有不同射线参数的平面波道集,射线参数p呈线性变化,平面波道集数为11个。图9(a)为该复杂模型的真实速度模型,图9(b)为偏移速度场。
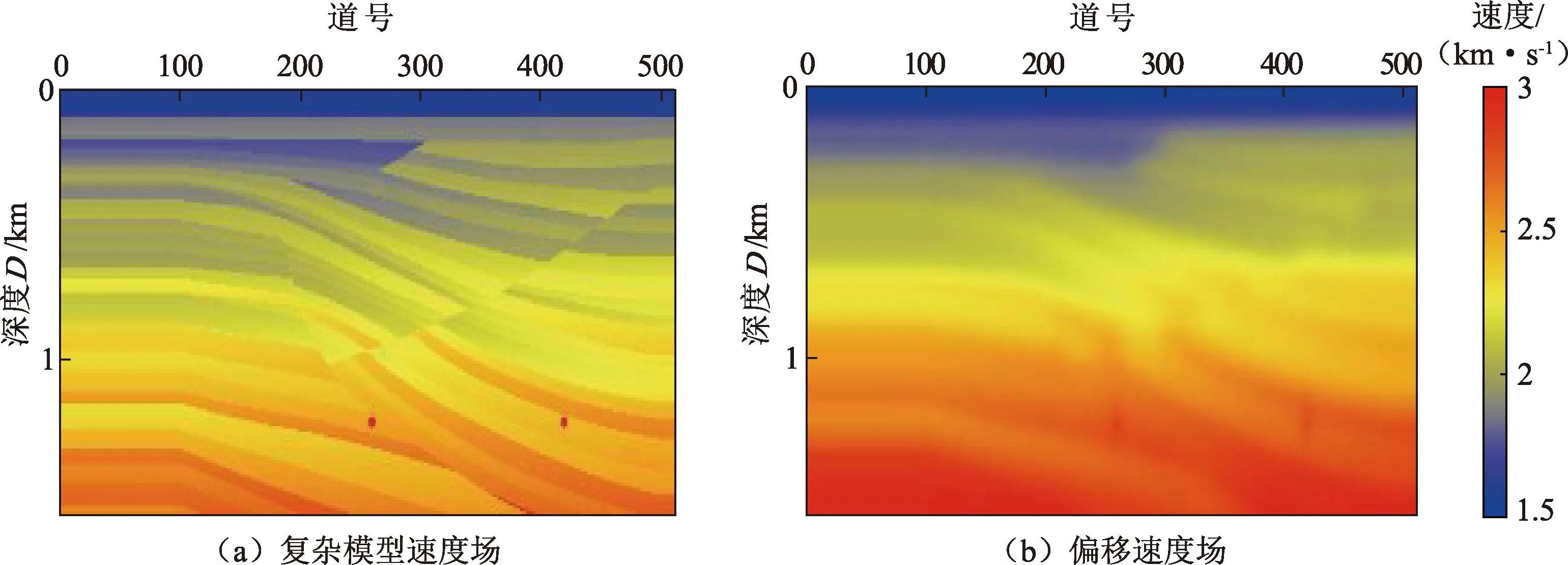
图9 复杂模型速度场和偏移速度场Fig.9 Velocity Field of complex model and migration velocity field
先分别对复杂模型进行PLSRTM迭代15次和35次,得到成像结果(图10(a)、(b))。由图10(a)、(b),经过15次和35次迭代的平面波最小二乘逆时偏移后,偏移结果中的构造成像效果较好、断层边界较为清楚,但存在较为严重的串扰噪声,这是由于多炮数据混叠在一个道集中所带来的噪音,且浅层部分存在一定的采集脚印。迭代35次的成像结果比迭代15次的成像结果更为清晰且串扰噪音更少。图10(c)、(d)分别是复杂模型经过Seislet软阈值算法约束和Seislet分数阶阈值函数约束的PLSRTM迭代15次后的成像结果。由图10(c)、(d)可知,在Seislet约束的平面波最小二乘逆时偏移后的结果中,串扰噪声都得到了一定的压制,对断层边界的成像效果都很好,但Seislet分数阶阈值函数的约束效果优于Seislet软阈值函数的约束效果,具体见红圈。图10(e)、(f)分别是复杂模型经过Seislet软阈值函数约束和Seislet分数阶阈值函数约束的PLSRTM迭代35次后的成像结果。图10(e)在部分反射轴附近仍存在部分串扰噪音,图10(f)的串扰噪音几乎被压制,浅层的采集脚印也得到一定的压制,具体位置见红圈。Seislet分数阶阈值函数的约束效果明显好于Seislet软阈值函数的约束效果。

图10 复杂模型下不同Seislet阈值函数约束的PLSRTM对比Fig.10 Comparison of PLSRTM with different Seislet threshold function constraints in complex model
虽然增加平面波道集的数量可以一定程度地提高PLSRTM的成像质量,压制串扰噪音,但会增加计算量。本文中先分别使用30个平面波道集的PLSRTM迭代15和35次后,得到偏移结果(图11(a)、(c))。图11(b)、(d)为使用11个平面波道集且经过Seislet分数阶阈值函数约束的PLSRTM迭代15和35次后的结果。由图11(a)、(b)、(c)、(d)可知,使用30个平面波道集的PLSRTM结果(图11(a)、(c))比未经过约束使用11个平面波道集的PLSRTM结果(图10(a)、(b))噪音更少,成像质量更高,但使用11个平面波道集且采用Seislet分数阶阈值函数约束的PLSRTM(图11(b)、(d)),其串扰噪音被压制得更为彻底,具有和使用较多平面波道集的传统PLSRTM相同的成像效果。再将使用11个道集的约束PLSRTM、11个道集的传统方法,以及30个道集的传统方法进行运算时间对比。
由表1可知,经过约束且使用11个平面波道集的PLSRTM时间略少于使用11个平面波道集的传统PLSRTM,更少于使用30个平面波道集的传统PLSRTM。因此该方法能够一定程度地提高计算效率。

表1 运算时间对比Table 1 Calculation time comparison s

图11 使用不同平面波道集数目下的PLSRTM与约束PLSRTM对比Fig.11 Comparison between PLSRTM and constrained PLSRTM using different number of plane-wave gather
对复杂模型进行偏移成像后,分别抽取其第150道、350道和200道作单道振幅对比(图12)。在图12(a)、(b)中,蓝色虚线为经过Seislet分数阶阈值算法约束的PLSRTM迭代20次后的振幅,橘色实线为经过PLSRTM迭代20次后的振幅,黄色为真实反射系数。从图12(a)、(b)中可以看出,经过Seislet分数阶阈值算法约束的20次迭代PLSRTM结果保幅性更好,更加收敛于真实的反射系数,成像更为准确,且振幅曲线波动更小,相对于未约束的PLSRTM抗噪能力更强。由图12(c),对11个道集的Seislet分数阶阈值函数约束的PLSRTM、11个道集的传统方法,以及30个道集的传统方法迭代第20次结果抽取第200道对比后,经过约束的PLSRTM结果更加收敛于真实的反射系数,具有更好的保幅性。
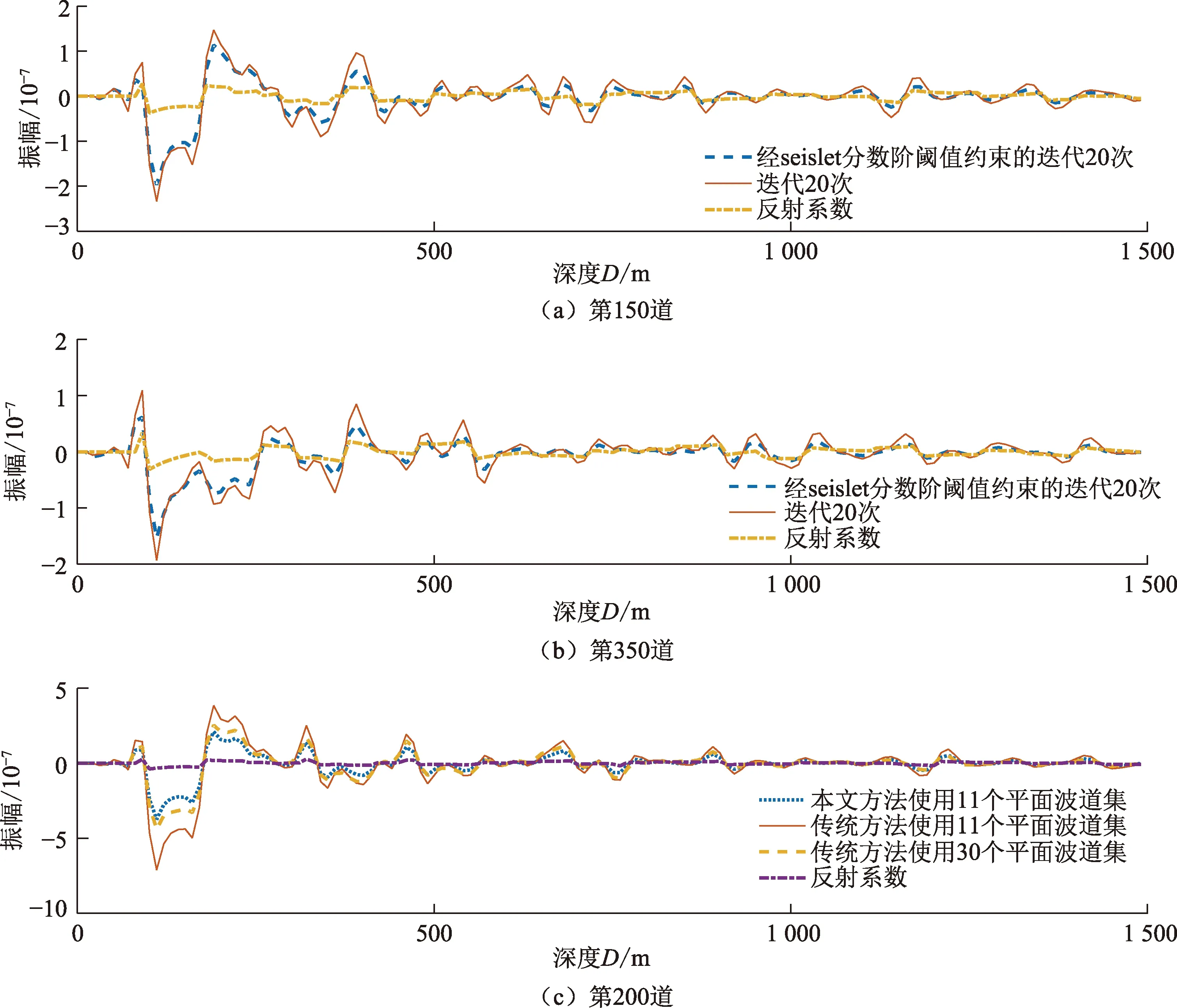
图12 复杂模型单道振幅对比Fig.12 Single-trace amplitude comparison of complex model
为了进一步验证本文方法对噪声的适应性,对所有炮集添加随机噪声,使其信噪比为2 dB。再对炮集进行平面波编码,得到11个平面波道集, (图13)。计算信噪比RSN的方法为能量叠加法[28],公式如下:

(17)
式中,M为时间采样点;N为道数;xij为第j道第i点的振幅。再分别进行Seislet分数阶阈值算法约束的PLSRTM和传统方法PLSRTM,并分别抽取第15次和第35次迭代结果进行分析(图14)。由图14可知,传统方法PLSRTM结果的噪音较为严重,尤其在构造附近,而经过Seislet分数阶阈值算法约束的PLSRTM后,噪音得到有效压制,且仍然能够较好地还原构造。

图13 射线参数p为0的含噪声平面波道Fig.13 Plane-wave gather for p=0 ms/m encoded by shot data with noise

图14 含噪声下的PLSRTM与约束PLSRTM对比Fig.14 Comparison between PLSRTM and constrained PLSRTM using plane-wave gather with noise
4 结 论
(1)Seislet变换测试表明,地震数据在Seislet域具有较好的稀疏性,但在使用阈值法进行地震数据重构时阈值不宜太小,以免丢失部分有效信息。
(2)数值测试中的模型测试和单道振幅测试表明,Seislet分数阶阈值算法约束的PLSRTM能够在传统PLSRTM的串扰噪音较强和保幅性等方面得到改善,且Seislet分数阶阈值算法比Seislet软阈值算法性能更优越。含噪数据测试结果表明,本文算法约束的PLSRTM能够在炮记录含噪的情况下得到较好的成像结果。
(3)基于Seislet分数阶阈值算法约束的PLSRTM可以使用较少的平面波道集达到与传统PLSRTM相同的成像效果,且运行时间也少于传统PLSRTM,提高了计算效率。
(4)Seislet变换对倾角过于依赖,倾角预测不精确时容易对成像造成影响,以后可以在如何减弱Seislet对倾角依赖的方面进行改进。

