航空弓形结构框喷丸强化变形计算及工艺规范建立
蒋建军,陈飞,门向南,钞欣,方丁,王成雨,李伟刚,杨杰
航空弓形结构框喷丸强化变形计算及工艺规范建立
蒋建军1,陈飞2,门向南1,钞欣1,方丁1,王成雨2,李伟刚2,杨杰2
(1.成都飞机工业(集团)有限责任公司,成都 610092;2.西南交通大学 力学与工程学院,成都 610031)
研究航空弓形结构框喷丸强化变形的力学理论、有限元模拟的预测方法,建立喷丸强化工艺规范,为国内航空工业中的喷丸工艺提供一定指导。首先利用有限元软件ABAQUS进行若干组不同喷丸速度的随机弹丸撞击模拟,创建与喷丸平均速度相关的喷丸诱导应力数据库,在此基础上,进行弓形结构框喷丸强化变形的理论预测和有限元仿真。在ABAQUS环境下开发一个快速模拟不同喷丸参数下弓形结构框喷丸强化变形的插件,实现各种不同类型的弓形结构框的自动前处理以及理论解和仿真解的给出。在以上研究的基础上,发展一套快速确定各类弓形结构框喷丸强化参数的工艺规范。针对某型号弓形结构框,在相同的喷丸参数下,理论计算的最大变形量为1.25 mm,有限元计算的最大变形量为1.13 mm,实验结果为1.8 mm。结合计算预测和工艺规范,确定了喷丸矫形区域及参数,最终弓形结构框的变形为0.15 mm,满足精度要求,验证了计算预测与规范的有效性。分析认为,建立的理论预测方法和有限元方法可以快速准确地预测弓形结构框喷丸强化变形结果。本研究对于国内航空工业中弓形结构框喷丸强化变形的快速仿真以及理论预测具有较大的工程价值。
喷丸;有限元仿真;弓形结构框;变截面梁;变形
在航空制造工业中,为了达到减轻质量和保证强度的目的,会使用较多高筋薄壁、结构复杂且精度要求较高的铝合金结构件。弓形结构框为其中一种典型的结构件,某型号飞机机头所使用的弓形结构框如图1所示。铝合金在加工成弓形结构框的过程中,由铣削、装夹等过程产生的残余应力,会引起构件尺寸发生变化,且内部的残余应力会严重影响结构框的疲劳强度,降低其使用寿命[1]。喷丸强化处理是提高构件疲劳强度和延长寿命的有效方法之一,在航空航天和汽车领域结构件的表面处理中有着广泛应用。由于弓形结构框为非对称结构,喷丸产生的残余压应力会使弓形结构框产生一定的变形,需要调整不同位置的喷丸强度以减小整体变形[2]。
喷丸变形在国内外有较多的研究。Miao等[3]建立了喷丸诱导应力与轴向约束力及约束弯矩之间的关系,并通过喷丸诱导应力计算了Almen试片的喷丸变形。肖旭东[4]基于等效喷丸诱导应力场,计算了喷丸对板料变形的影响。Gariépy等[5-6]通过实验和有限元模拟,研究了不同弹丸直径和不同喷丸速度对喷丸效果的影响,并将模拟弹丸撞击得到的喷丸应力场引入到大尺寸零件的有限元模型中,模拟零件变形。文献[7-9]建立了喷丸强化三维模型,并研究了不同喷丸参数对喷丸诱导应力分布的影响。张炜等[10]利用Box-Behnken实验和有限元分析,对机翼缘条喷丸参数进行了优化。
在实际喷丸强化工艺中,弓形结构框的种类繁多,且每一类的喷丸要求均不同,喷丸参数往往需要通过大量的重复实验来确定。另外,同一批次工件因其初始变形的不同,需要不同的喷丸参数。针对上述问题,本文进行了如下研究:首先利用ABAQUS进行随机多弹丸的喷丸模拟,建立喷丸诱导应力数据库;其次,研究了弓形结构框喷丸强化变形的力学理论和有限元仿真预测方法,在ABAQUS环境下开发了一个快速预测不同类型弓形结构框在不同喷丸强化参数下变形结果的插件,将理论预测方法集成于插件中,与ABAQUS共用模型数据,并在后处理中同时输出理论预测结果和有限元结果,结合具体的弓形结构框喷丸实验验证了该插件的有效性。在以上研究的基础上,形成了一套快速确定各类弓形结构框喷丸强化参数的工艺规范。
1 喷丸诱导应力数据库建立
根据Gariépy等[6]对大尺寸零件喷丸模拟方法的研究,本文采用直接应力法来模拟结构框的喷丸强化变形。首先通过随机多弹丸撞击模拟获得了如图2所示的多组喷丸诱导应力曲线,结合不同喷丸参数下的诱导应力曲线,可以建立喷丸参数与喷丸诱导应力之间的关系,在此基础上建立喷丸诱导应力数据库。然后利用有限元模拟和理论计算快速预测弓形结构框在不同弹丸速度下的喷丸强化变形。在计算过程中,直接考虑的喷丸参数为喷丸速度,但在实际喷丸的时候,喷丸速度不便直接测量,利用Dr. KIemenz[11]推导出的经验公式计算:
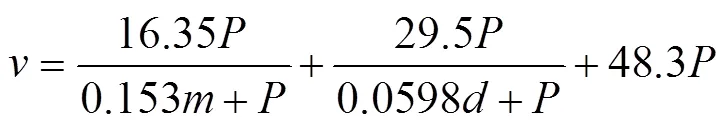
式(1)中:为弹丸平均速度,m/s;为喷丸压力,MPa;为弹丸直径,mm;为弹丸流量,kg/min。其中,喷丸压力、弹丸直径和弹丸流量可根据具体喷丸工况直接给出。
图2 不同速度下的诱导应力沿厚度分布
Fig.2 Induced stress distribution along the thickness at different speeds
具体的随机弹丸撞击模型如图3所示。此模型已经对网格尺寸的收敛性、模型的边界效应以及约束方式等进行了分析,其收敛性良好,且计算结果稳定。模型中,弹丸是直径为0.58 mm的球体,初速度为50 m/s,为减少计算时间,弹丸在模拟过程中被视作刚体。靶材的几何尺寸为5.5 mm×5.5 mm×2 mm,为了避免边界对结果的影响,弹丸全部作用在靶材上表面中心的2 mm×2 mm的区域内,且只统计中心1 mm×1 mm区域内的数据。靶材侧面设置对称约束,靶材底面全固定。为确保计算结果的精度和最终所得应力曲线的平滑度,对弹丸撞击区域内的网格进行了加密处理,单元尺寸为0.02 mm,非撞击区域的网格尺寸为0.1 mm,单元类型为8节点的减缩单元(C3D8R)[12]。采用动态显式分析,靶材与弹丸间的接触设为罚函数法,接触摩擦系数为0.03。弹丸和靶材的材料参数见表1,靶材采用Johnson-Cook本构模型参数,见表2[13]。

图3 多弹丸撞击模拟模型
表1 弹丸和靶材的材料属性

Tab.1 Material properties of shots and targets
表2 7075铝合金Johnson-Cook本构模型参数

Tab.2 Johnson-Cook constitutive model parameters of 7075 aluminum alloy
2 理论及有限元预测弓形结构框变形
在诱导应力数据库的基础上,本文同时采用解析计算和有限元模拟对喷丸强化后的工件变形进行预测。解析计算方法基于弹性力学,将喷丸诱导应力等效为弯矩,根据梁的弯曲理论,建立结构框喷丸诱导应力与变形方程,得到了结构框喷丸变形。有限元模拟方法则选取直接应力法,采用3层结构的复合材料常规壳单元,外侧两层用来定义初始应力,中间层用于调整模型厚度。
2.1 理论模型
根据航空弓形结构框的结构特点,将其简化成轴线为弧线、横截面为“T”形且相对轴线平面对称的变截面曲梁。如图4所示,轴为弧形件轴线,轴线半径为,轴沿截面法向,轴为弧形件横截面的对称轴,轴在横截面上,且垂直于轴、轴。

图4 简化几何模型
弧形件截面高度远小于其轴线曲率半径,因此假定弧形件纯弯曲时的中性层位于轴。弧形件在进行喷丸强化时,受喷面相对其几何对称面对称。喷丸强化工艺完成后,其变形以对称面内的弯曲及延展变形为主,可视为变截面曲梁的平面变形。
初始状态下,完全约束弧形件变形。σ可以等效为与边界上约束力相平衡的等效轴向力和弯矩:

式中:是横截面面积。根据曲梁平面弯曲理论,边界条件撤除后弧形件变形方程为:
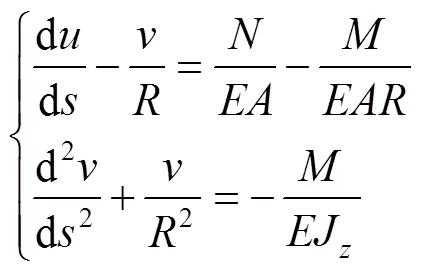
2.2 有限元模拟
由于弓形结构框的几何实体外形轮廓比较复杂,为了保证数值模拟的可行性,并合理节省计算时间,方便网格划分,进行有限元模拟时,对几何模型进行了适当的简化,如图5所示。
泡沫塑料也是现代立体漆艺常用的造型材料。泡沫塑料质地轻,容易切削成型。成型之后可以留在作品内部,起支撑作用;也可以将其去除。这只需要在成型的胎骨上凿一个小孔,用针管注入松香水等稀释剂,即可使泡沫塑料溶解,随后让溶解成的液体从小孔流出,封上小孔即可。闽江学院美术学院学生陈健的作品《容·屿》(图5)便是用塑料泡沫制作胎骨。作品表现了海水惊涛拍岸的汹涌来势,以及岛屿处变不惊的从容气度。

图5 有限元壳单元模型
将模型分段是为了方便将不同的材料厚度赋予给相应工件部位。首先约束模型3个顶点位移自由度,以防止模型产生刚体位移。然后利用ABAQUS子程序将已获得的诱导应力施加到相应的壳单元节点上,最后模拟得到结构框的喷丸变形结果,如图6所示。
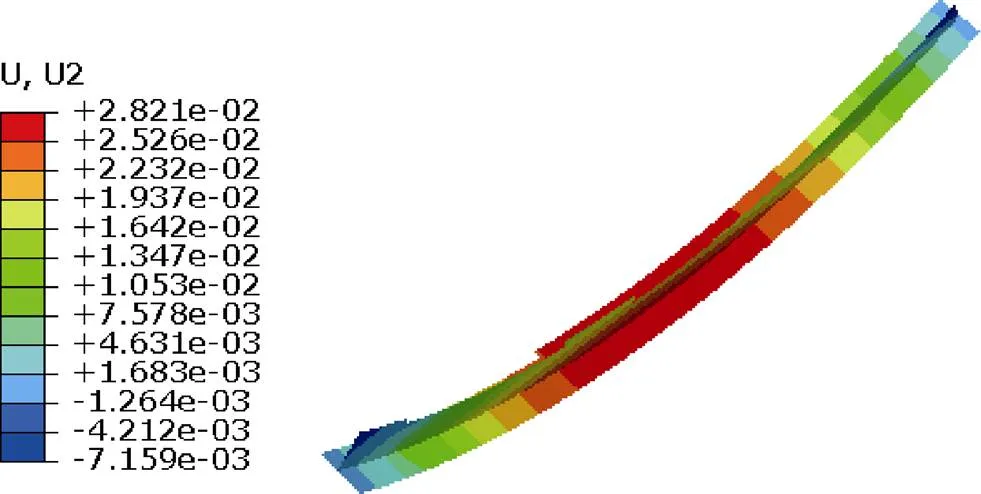
图6 喷丸强化变形结果
3 ABAQUS二次开发
3.1 程序框架
本节基于ABAQUS的 Plug-ins 插件程序,通过GUI脚本创建新的用户图形界面,实现与用户的人机交互[14]。使用 Python 语言编写内核脚本程序,通过设计合理的参数对话框和定义关键字,开发出一个用户定制功能的弓形结构框喷丸模拟仿真模块,使ABAQUS可自动完成不同种类弓型结构框的有限元分析。包括几何建模、边界条件施加、网格划分和子程序SIGINI自动施加等操作,有效提高了弓形结构框喷丸强化数值模拟的效率[15]。子程序中的诱导应力数据将由用户输入的喷丸参数决定。另外,将理论预测模型集成于仿真模块中,与ABAQUS共用模型数据和喷丸参数,在用户使用Plug-ins插件并开始有限元计算时,理论计算程序自动提交运算,并将理论预测结果和ABAQUS模拟结果同时输出。程序流程如图7所示。

图7 程序流程
3.2 前、后处理模块
插件中,前处理包含了两个输入界面。模型参数输入界面如图8所示,界面直接定义了工作目录、弓形结构框总分段数、每一段的截面参数、腹板与外形间的夹角、半径、网格尺寸和材料类型等7个参数,其中的截面参数包含了界面中表格里面的8个参数。喷丸参数如图9所示,喷丸面介绍如图10所示。输入的参数为各个喷丸面的喷丸压力、每分钟喷丸量、弹丸直径和喷丸角度。输入的模型参数和喷丸参数为理论计算和有限元仿真共用参数。从参数输入界面可以看出,该插件可适用于任意变截面弓形结构框在不同喷丸参数下喷丸强化模拟。为了更直观地查看弓形结构框喷丸强化后的变形量,在ABAQUS完成计算后,提取相应节点的两个主方向的位移结果,利用三角关系求解出喷丸后弓形结构框沿其半径方向的位移,并将ABAQUS模拟结果同理论预测结果同时输出在ABAQUS操作界面下方的显示状态信息栏。
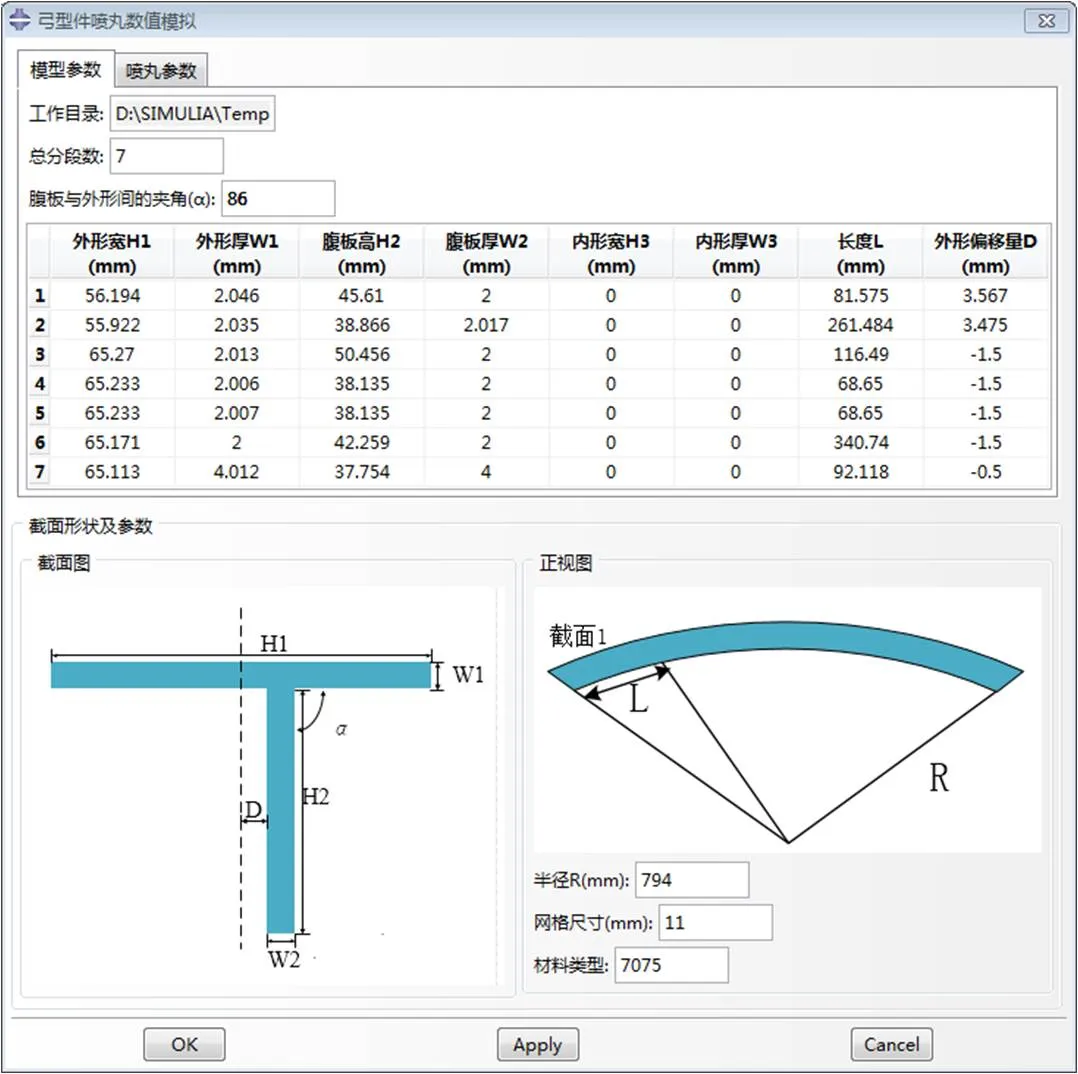
图8 模型参数界面
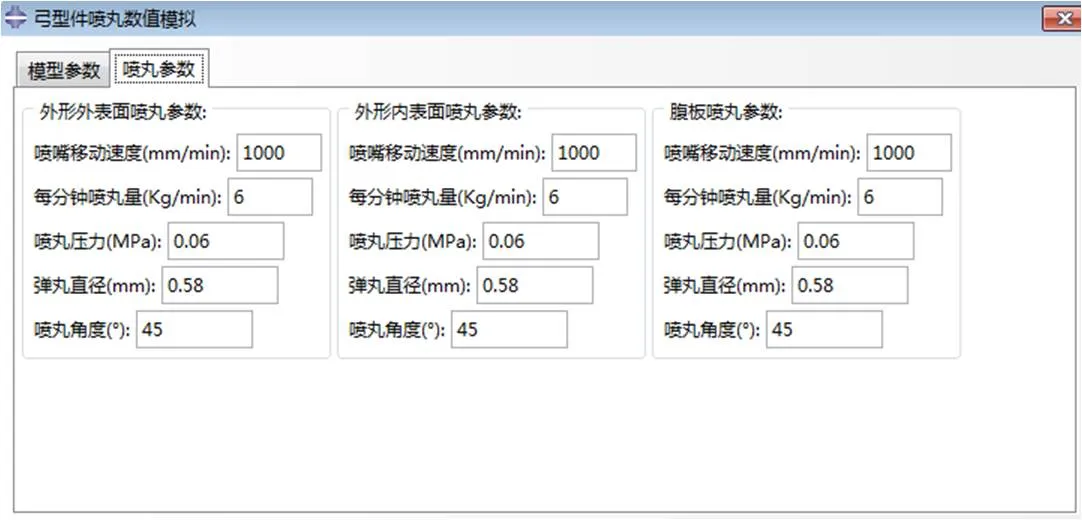
图9 喷丸参数界面
4 理论计算与有限元仿真验证
为了验证理论预测和有限元模拟结果的可靠性,利用具体弓形结构框的喷丸实验来加以验证。针对如图11所示的弓形结构框,按照实际的喷丸要求,对弓形结构框的外形内外表面使用相同的喷丸参数进行喷丸实验、理论预测和数值模拟。

图11 实验工件
4.1 有限元及理论计算结果
根据第3节的介绍,利用喷丸强化插件计算的位移云图如图12所示。同一喷丸参数下,理论预测出工件的最大变形量为1.25 mm,有限元模拟出最大变形量为1.13 mm。理论预测和有限模拟结果基本一致。
4.2 喷丸实验和变形测量
现场的喷丸实验如图13所示,将弓形结构框固定在工作平台上进行喷丸。分别将喷丸前后的弓形结构框放置在检夹模具上,利用塞尺测量弓形结构框与检夹模具之间的间隙,然后对比喷丸前后间隙的变化,确定弓形结构框的喷丸强化变形量,并记录相关数据。

图12 有限元模拟结果

a 喷丸过程
b 贴模测量
图13 喷丸实验件
Fig.13 Shot peening test piece: a)shot peening process; b)die sticking measurement
4.3 计算与实验对比
相同喷丸参数下,计算与实验的最大变形量见表3。将实验结果与计算结果对比发现,计算结果较实验结果偏小。由于喷丸过后,工件的变形量过大,无法满足精度要求,后续利用工艺规范确定了喷丸矫形区域(腹板面)及参数,最终喷丸过后工件的变形量为0.15 mm,达到了喷丸变形要求。
表3 最大变形量比较

Tab.3 Comparison of maximum deformation
5 工艺规范
5.1 喷丸强化工艺总体流程
理论和有限元虽然可以快速预测不同类型弓形结构框喷丸强化变形结果,但是由于实际工艺的复杂性,有必要建立具有操作性的规范。针对成都飞机工业(集团)有限责任公司的喷丸工艺,结合有限元仿真及理论预测,建立了一套适用于各类弓形结构框喷丸强化的工艺规范,如图14。利用此规范的方法,修正了成飞公司某零件的喷丸参数,最终零件的变形误差在生产要求的±0.2 mm之内。

图14 工艺规范基本思路
5.2 确定喷丸强度与气压关系
实际喷丸过程中,可变的喷丸参数较多,包括喷丸气压、弹流量、喷丸角度、弹丸直径和喷嘴移动速度。为实现少参数下控制喷丸变形结果,固定非关键因素(弹流量、喷丸角度、弹丸直径和喷嘴移动速度),在许可范围内调整喷丸气压来控制喷丸变形。通过Almen喷丸实验确定了S230弹丸类型下喷丸气压与喷丸强度之间的关系曲线,如图15所示。
5.3 确定喷丸基准面及其喷丸强度初始值
根据具体结构框的喷丸要求,首先确定喷丸基准面,然后以规定许可喷丸强度的中间值作为基准面的喷丸强度,通过改变其他面的喷丸强度来调整喷丸强化的变形量。
5.4 计算变形与喷丸强度的关系
针对相应的喷丸设备,固定零件基准面的喷丸强度,利用弓形结构框喷丸强化插件计算零件沿半径方向的最大变形量随调整面喷丸强度的变化曲线,结果如图16所示。
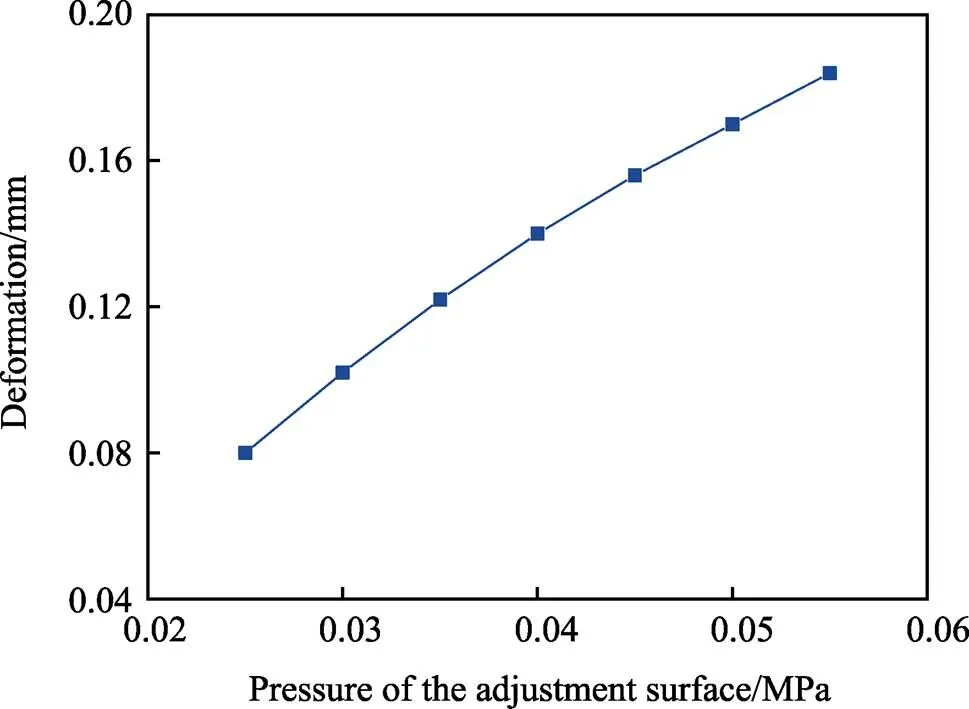
图16 S230弹丸喷丸强度和变形的关系
5.5 喷丸工艺流程
1)第一件初始变形尺寸测量,选择第一个零件,利用检夹模具和塞尺测量初始的变形量,记录内收尺寸或者外扩尺寸。
2)利用弓形结构框喷丸强化软件,计算获得喷丸强度的值,使得零件的变形量补偿初始变形。
3)按照计算得到的喷丸强度依次对零件基准面和调整面进行喷丸,利用检夹模具实际测量零件变形量。通过插值方法获得计算的补偿系数。
4)针对接下来的每一个件,检测初始变形量,采用有限元仿真并对结果进行计算补偿,进行喷丸。
6 结论
喷丸工艺在国内外已有较多的研究,但是由于实际喷丸的复杂性,目前喷丸研究仍然还不完善。本文针对航空弓形结构框的喷丸工艺进行了深入的研究,主要研究成果如下:
1)建立了喷丸诱导应力数据库,建立了弓形结构框喷丸变形的理论计算方法和有限元模拟方法,开发了快速预测弓形结构框喷丸变形结果的插件,通过具体的实验验证了插件计算结果的有效性和准确性。
2)针对成都飞机工业(集团)有限责任公司的喷丸工艺,结合有限元仿真及理论预测,建立了一套各类弓形结构框喷丸强化的工艺规范。该套工艺规范的建立对快速确定各类弓形结构框的喷丸参数具有较大的工程价值。
[1] 荣祖兰. 表面喷丸改善铝合金高周疲劳寿命的实验研究[J]. 热加工工艺, 2016, 45(4): 134-136. RONG Zu-lan. Experimental study on high-cycle fatigue life enhancement of shot-peening Al alloy[J]. Hot working technology, 2016, 45(4): 134-136.
[2] 陈家伟, 廖凯, 车兴飞, 等. 铝合金喷丸应力-变形的仿真分析与实验[J]. 表面技术, 2018, 47(11): 41-47. CHEN Jia-wei, LIAO Kai, CHE Xing-fei, et al. Simulation analysis and experiment of surface stress-deformation on Al-based alloy by shot peening[J]. Surface technology, 2018, 47(11): 41-47.
[3] MIAO H Y, LAROSE S, PERRON C, et al. An analytical approach to relate shot peening parameters to almen intensity[J]. Surface and coatings technology, 2010, 205(7): 2055-2066.
[4] 肖旭东. 弹丸喷丸应力场建模与条带喷丸整体变形模拟[D]. 西安: 西北工业大学, 2015. XIAO Xu-dong. Modelling of shot peening stresses and simulation of integral deformation of strip peening forming[D]. Xi′an: Northwestern Polytechnical University, 2015.
[5] GARIÉPY A, MIAO H Y, LÉVESQUE M. Simulation of the shot peening process with variable shot diameters and impacting velocities[J]. Advances in engineering software, 2017, 114: 121-133.
[6] GARIÉPY A, LAROSE S, PERRON C, et al. Shot peening and peen forming finite element modeling—Towards a quantitative method[J]. International journal of solids and structures, 2011, 48(20): 2859-2877.
[7] 张洪伟, 陈家庆, 张以都. 基于多丸粒模型的喷丸表面强化过程数值模拟[J]. 塑性工程学报, 2012, 19(6): 118-125. ZHANG Hong-wei, CHEN Jia-qing, ZHANG Yi-du. Numerical simulation of shot-peening process based on multiple shot model[J]. Journal of plasticity engineering, 2012, 19(6): 118-125.
[8] 张洪伟, 张以都, 吴琼. 喷丸强化残余应力场三维数值分析[J]. 航空动力学报, 2012, 25(3): 603-609. ZHANG Hong-wei, ZHANG Yi-du, WU Qiong. Three- dimensional numerical analysis of residual stress field for shot-peening[J]. Journal of aerospace power, 2012, 25(3): 603-609.
[9] 王明涛, 曾元松, 尚建勤, 等. 基于ABAQUS的大尺寸弹丸喷丸过程数值模拟[J]. 塑性工程学报, 2012, 19(5): 109-114. WANG Ming-tao, ZENG Yuan-song, SHANG Jian-qin, et al. Numerical simulations of shot peening with large balls based on ABAQUS[J]. Journal of plasticity engineering, 2012, 19(5): 109-114.
[10] 张炜, 刘立彬, 夏明莉, 等. 机翼缘条喷丸强化变形模拟与参数优化[J]. 航空制造技术, 2016(17): 28-32. ZHANG Wei, LIU Li-bin, XIA Ming-li, et al. Simulation and optimization of shot peening deformation for aircraft wing flange[J]. Aeronautical manufacturing technology, 2016(17): 28-32.
[11] KLEMENZ M. Anwendung der simulation der randschicht ausbildung beim kugelstrahlen auf die abschätzung der schwingfestigkeit gekerbter bauteile[D]. Shaker Aachen: Universität Karlsruhe, 2009.
[12] 张少波, 布紫叶. 2024铝合金随机多弹丸喷丸后残余应力场的有限元模拟[J]. 机械工程材料, 2016, 40(7): 87-90. ZHANG Shao-bo, BU Zi-ye. Finite element simulation on residual stress field of 2024 aluminum alloy after shot peening with number of random projectiles[J]. Materials of mechanical engineering, 2016, 40(7): 87-90.
[13] 李源, 雷丽萍, 曾攀. 弹丸束喷丸有限元模型数值模拟及实验研究[J]. 机械工程学报, 2011, 47(22): 43-48. LI Yuan, LEI Li-ping, ZENG Pan. Shot stream finite element model for shot peening numerical simulation and its experiment study[J]. Journal of mechanical engineering, 2011, 47(22): 43-48.
[14] 黄霖. Abaqus/CAE二次开发功能与应用实例[J]. 计算机辅助工程, 2011, 20(4): 96-100. HUANG Lin. Secondary development functions and applications of Abaqus/CAE[J]. Computer aided engineering, 2011, 20(4): 96-100.
[15] 杨德锴, 刘长安, 牛强, 等. 金属板料抛喷丸仿真的有限元方法[J]. 机械科学与技术, 2010, 29(6): 836-840. YANG De-kai, LIU Chang-an, NIU Qiang, et al. Finite element method for shot blasting and shot peening simulation of metal sheet[J]. Mechanical science and technology for aerospace engineering, 2010, 29(6): 836-840.
Calculation of Shot Peening Strengthening Deformation of Aerospace Arc-shaped Frame and Establishment of Process Specification
1,2,1,1,1,2,2,2
(1.Chengdu Aircraft Industry (Group) Co., Ltd, Chengdu 610092, China; 2.School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)
This work aims to study the mechanical theory and finite element method (FEM) prediction method for shot peening deformation of aerospace arc-shaped frame, and establish the specification of shot peening process to provide guidance for shot peening in the domestic aviation industry. Firstly, several groups of random shot impact simulations with different shot speeds were carried out by ABAQUS, and a shot peening induced stress database related to the average shot speed was created. Based on this, theoretical prediction and finite element simulation of shot peening deformation of arc-shaped frame were carried out; in the ABAQUS environment, a plug-in for quickly simulating the shot peening deformation of arc-shaped frame under different peening parameters was developed. By using this plug-in, all operations could be done automatically in the fore treatments of ABAQUS for various types of arc-shaped frames, and theoretical and simulation results could be given at the same time. Based on the above research, a process specification for quickly determining the shot peening parameters of various arc-shaped frames was developed. For specific aerospace arc-shaped frame, the theoretical maximum deformation was 1.25 mm; the maximum deformation calculated by FEM was 1.13 mm; and the experimental result was 1.8 mm under the same shot parameters. Combined with calculation prediction and process specification, the shot peening area and parameters were determined; and the final deformation of the arc-shaped frame was 0.15 mm, which met the accuracy requirements. The validity of the calculation prediction and specification was verified. Through the analysis, theoretical prediction method and FEM can quickly and accurately predict the results of shot peening deformation of arc-shaped frame. This study is of engineering value for the quick simulation and theoretical prediction of the shot peening deformation results of the arc-shaped frame in the domestic aviation industry.
shot peening; finite element simulation; arc-shaped frame; beam with variable cross-section; deformation
2019-06-21;
2019-09-09
JIANG Jian-jun (1970—), Male, Master, Researcher level senior engineer, Research focus: aeronautical engineering.
杨杰(1970—),男,博士,教授,主要研究方向为工程力学。E-mail: yangchenjie@swjtu.cn
Corresponding author:YANG Jie (1970—), Male, Doctor, Professor, Research focus: mechanics of Engineering. E-mail: yangchenjie@swjtu.cn
蒋建军, 陈飞, 门向南, 等. 航空弓形结构框喷丸强化变形计算及工艺规范建立[J]. 表面技术, 2020, 49(6): 290-296.
TG668
A
1001-3660(2020)06-0290-07
10.16490/j.cnki.issn.1001-3660.2020.06.035
2019-06-21;
2019-09-09
蒋建军(1970—),男,硕士,研究员级高级工程师,主要研究方向为航空工程。
JIANG Jian-jun, CHEN Fei, MEN Xiang-nan, et al. Calculation of shot peening strengthening deformation of aerospace arc-shaped frame and establishment of process specification[J]. Surface technology, 2020, 49(6): 290-296.

