二次喷丸42CrMo钢表面完整性的数值模拟研究
何嘉禧,汪舟,甘进,杨莹,王晓丽,石明,任旭东
二次喷丸42CrMo钢表面完整性的数值模拟研究
何嘉禧1,汪舟1,甘进2,杨莹1,王晓丽1,石明1,任旭东1
(1.武汉理工大学 a.汽车工程学院 b.现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学 交通学院,武汉 430063)
目的探究二次喷丸工艺参数对42CrMo钢零件表面完整性的影响规律。方法建立三维随机喷丸有限元模型,并通过实验验证有限元模型预测残余应力的准确性。将一次喷丸后零件的表面形貌和应力应变结果作为初始状态导入到二次喷丸模型中,构建出二次喷丸预测模型。分析二次喷丸参数对42CrMo钢零件表面残余应力场、表面粗糙度以及等效塑性形变场的影响情况。结果二次喷丸后,42CrMo钢零件近表层(0~100 μm)的残余压应力值均比初始状态有所增加。增加二次喷丸覆盖率对表面残余应力的提升作用最为明显,最大可比初始状态提高63.3%,而增加二次喷丸直径对残余应力的改善效果最不明显。过度增加二次喷丸速度会导致表面粗糙度明显增加,提高二次喷丸覆盖率可显著降低表面粗糙度,覆盖率为300%时,粗糙度比初始状态减小了14.4%。表层PEEQ值随着二次喷丸速度、弹丸直径和覆盖率的增加而增加,但当二次喷丸速度、弹丸直径和覆盖率增加到一定程度后,表层PEEQ值会趋于饱和。结论二次喷丸预测模型揭示了二次喷丸参数与42CrMo钢零件表面完整性之间的影响规律,为二次喷丸的工业应用提供了一定的参考意义。
二次喷丸;有限元模拟;表面完整性;残余应力;等效塑性形变;表面粗糙度
喷丸是一种利用大量高速弹丸撞击零件表面来提高金属疲劳寿命的机械表面强化工艺。它通过向零件表层引入残余压应力来阻碍金属表面裂纹的萌生和扩展[1-3],同时还能使零件近表层产生晶粒细化和加工硬化[4-5],提高零件的抗疲劳和抗应力腐蚀能力[6]。喷丸强化工艺不受材料种类和几何形状尺寸的限制,因此被广泛运用于机械制造、船舶、航天航空、汽车生产等领域[7]。二次喷丸是在传统喷丸的基础上,通过比一次喷丸强度更小的弹丸流撞击零件表面,来进一步改善喷丸强化效果,其在工业界有着广泛的应用前景。
随着计算机技术的迅猛发展,利用计算机模拟分析喷丸工艺过程已经成为喷丸领域不可或缺的研究手段之一。近几十年来,众多学者在喷丸有限元仿真上做了许多有意义的工作。Bagherifard等人[8]利用三维有限元模型预测高能喷丸对表面纳米结构的影响,提出了一种利用等效塑性形变值来判断纳米层生成的数值方法,最后分析了喷丸参数与残余应力、加工硬化和纳米层深度之间的关系。Miao等人[9]考虑了弹丸空间分布的随机性,联合Matlab和ANSYS建立了随机喷丸模型,并研究了弹丸数量与喷丸强度、覆盖率和粗糙度之间的数值关系,结果表明,该随机喷丸模型对喷丸强化效果的预测比传统喷丸模型更准确。Hong等人[10]结合有限元和离散元研究了弹丸入射和回弹过程中的接触问题,并揭示了喷丸工艺参数对残余应力的影响规律。梁若等人[11]提出了34CrNiMo6钢随机多弹丸的周期性有限元模型,并分析了复合喷丸的强化效果以及不同喷丸强度对残余应力场的影响。赵莉莉等人[12]利用分批顺序撞击的9丸粒有限元模型,研究了弹丸速度、重复打击次数、搭接率以及多丸粒分布对残余压应力的影响,为获得理想残余应力提供了理论依据。
之前的喷丸数值模拟工作绝大部分都仅围绕一次喷丸展开,学术界针对二次喷丸强化效果的模拟研究相对较少。而在实际生产中,二次喷丸可进一步提高零件的表面残余压应力值,并降低表面粗糙度,因此对二次喷丸进行仿真具有重要的研究意义[11]。本文结合ABAQUS和Python程序,建立了二次喷丸预测模型,系统地分析了二次喷丸参数对受喷零件表面残余应力、表面粗糙度和等效塑性形变的影响。研究结果可为二次喷丸仿真领域提供一定的参考价值。
1 三维随机喷丸有限元模型建立
本文采用有限元软件ABAQUS 6.10建立三维随机喷丸有限元模型,模型由42CrMo钢受喷零件以及空间上随机分布的弹塑性弹丸所组成,如图1所示。建模过程分为两步:1)通过一次喷丸仿真,获取一次喷丸后零件的表面形貌和应力应变结果;2)把计算结果作为初始状态导入到二次喷丸模型中,构建出二次喷丸预测模型,并完成后续仿真。前后两次仿真采用相同的受喷零件,零件模型为3 mm×3 mm× 10 mm的长方体,网格单元为减缩积分单元(C3D8R)。为了减少模型内部剪切波和膨胀波回弹对残余应力结果的影响,模型四周设置了无限边界条件,单元类型为无限单元(CIN3D8)。零件底面节点的自由度均被约束。选取零件中心1 mm×1 mm×2 mm的区域作为塑性变形观测区,并在该区域内分析残余应力、表面粗糙度和等效塑性形变,如图1b的中心区域所示。伍刚等人[13]的研究结果表明,网格密度对残余应力模拟结果有较大影响。综合考虑模拟结果的准确性和计算效率,设置观测区网格长度为0.02 mm,其他区域采用渐变网格。采用Python程序实现弹丸在三维空间上的随机分布,式(1)为弹丸中心点坐标的生成公式。

由于Johnson-cook模型考虑了应变硬化、应变率硬化以及温度软化对材料流动应力的影响,因此本文采用Johnson-cook模型作为零件材料的本构模型,如式(2)所示。
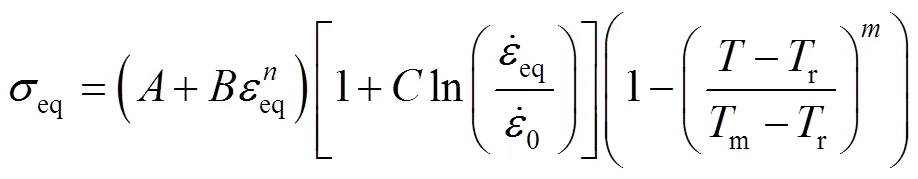
式中,、、、和分别代表环境温度(r)下的初始屈服应力、应变硬化参数、应变率敏感系数、温度软化系数和应变硬化指数。42CrMo钢的Johnson-cook模型参数如表1所示。弹丸的屈服强度为1550 MPa,密度为7850 kg/m3,杨氏模量为210 GPa,泊松比为0.3。
表1 42CrMo钢的Johnson-Cook本构模型参数

Tab.1 Johnson-Cook constitutive model parameters of 42CrMo steel
图2为随机喷丸模型弹坑示意图,采用Kirk[14]等人推导的公式,计算特定覆盖率下所需的弹丸数量:

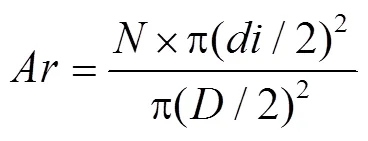
式中,为喷丸覆盖率,为中间变量,为弹丸数量,为单弹坑直径,为覆盖率计算区域的直径,取值为1 mm。表2为不同二次喷丸工艺参数和对应的弹丸数量。

图2 随机喷丸模型弹坑示意图[15]
为了准确评估零件表面残余应力和等效塑形形变(PEEQ),利用Python程序提取观测区沿层深各层节点的残余应力平均值和PEEQ平均值,提取范围为直径1 mm的圆,以便与X-ray实验测得的残余应力值进行对比。表面粗糙度采用轮廓算术平均偏差作为评价指标,利用Python程序计算受喷零件表面各节点的向位移量的算术平均偏差,得到各喷丸参数下的值。
表2 不同二次喷丸工艺参数和对应的弹丸数量

Tab.2 Different shot peening parameters and the corresponding number of shots
一次喷丸和二次喷丸的工艺参数如表3所示。除了图3中残余应力验证所用的一次喷丸参数为= 35 m/s、=0.56 mm、=100%以外,后续的二次喷丸仿真中采用的一次喷丸的速度、直径和覆盖率均为60 m/s、1 mm和100%。由于本文二次喷丸仿真参数较多,为了便于区分,对仿真组有如下定义:代表速度,代表直径,代表覆盖率。例如5006100代表速度为50 m/s,直径为0.6 mm,覆盖率为100%的仿真组。
表3 一次喷丸和二次喷丸的工艺参数

Tab.3 Process parameters of single shot peening and dual shot peening
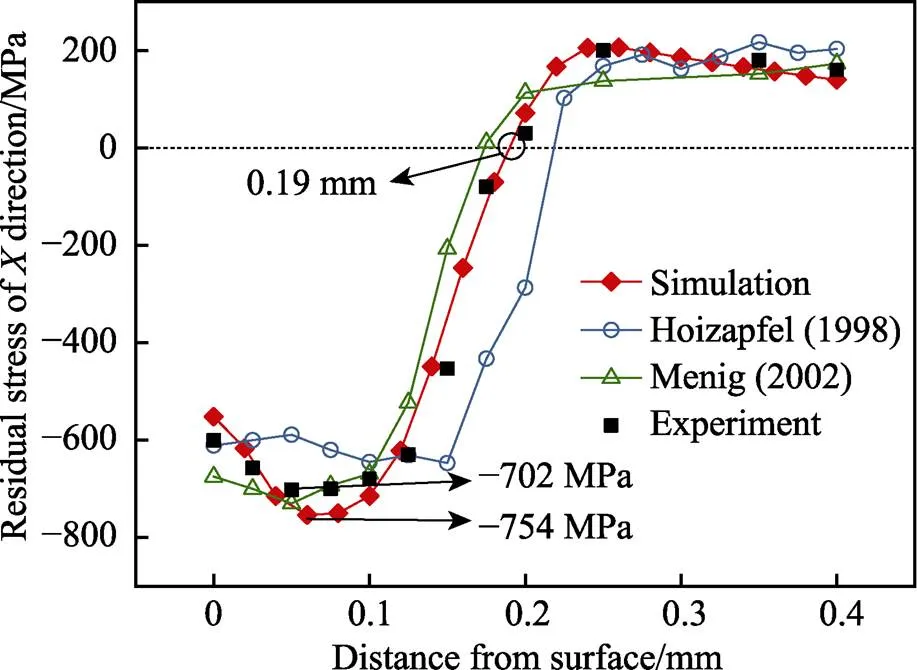
图3 一次喷丸后42CrMo钢零件的残余应力模拟和实验结果
图3为一次喷丸后42CrMo钢零件的残余应力模拟与实验结果,喷丸参数=35 m/s、=0.56 mm、= 100%,仿真弹丸数量=154。实验采用了Holzapfel[16]、Menig[17]的实验数据和学校实验室所测数据。由图可知,在应力曲线的形状和幅值方面,仿真值与三组实验值基本吻合,残余压应力层深在0.15~0.25 mm范围内,最大残余压应力层深在0.05~0.1 mm范围内。其中,仿真值和实验室所测值的表面残余应力分别为−552 MPa和−600 MPa,模拟误差为8.0%;最大残余压应力分别为−754 MPa和−702 MPa,模拟误差为7.4%;最大残余压应力层深和残余压应力层深基本一致。这表明所建喷丸模型对残余应力有较好的预测能力,能用于描述受喷零件表面残余应力的变化情况。
2 实验方法
采用42CrMo钢作为实验材料,其热加工工艺为850 ℃下淬火20 min(水冷),然后回火至650 ℃下保温2 h(空冷)。材料的初始屈服强度、抗拉强度和硬度分别为680 MPa、930 MPa和250HV。表4为42CrMo钢的化学成分。
表4 42CrMo钢化学成分

Tab.4 Chemical composition of 42CrMo steel wt.%
采用XN-9065P型气动式喷丸机,完成喷丸强化实验。根据Klemenz[18]的经验公式(5),建立仿真参数和实验参数之间的对应关系。

式中,为弹丸直径,为丸料进给流量,为喷丸压力,为弹丸速度。例如实验中=2 kg/min、=1 mm、=5 bar,由公式(5)可得弹丸的平均速度约为60 m/s。
残余应力通过X射线衍射仪和Mn-Kα辐射仪检测,根据sin2方法[19-20]分析γ-Fe(211)的衍射峰位移,在−70°~+70°范围内,每变化10°测定一次角。为了获取零件沿层深方向的残余应力,通过电解法对样品进行剥层处理,并根据Moore等人[21]提出的方法修正残余应力值。
3 结果与分析
3.1 二次喷丸参数对初始残余应力的影响
喷丸后,零件表层区域的残余应力场对喷丸材料疲劳性能的改善十分关键。为了准确评估残余应力场,通常定义表面残余应力、最大残余压应力、最大残余压应力层深以及残余压应力层深四个特征参数。
图4为二次喷丸中,弹丸直径为0.6 mm,覆盖率为100%,弹丸速度分别为50、60、80、100 m/s时,42CrMo钢零件方向的残余应力沿层深的分布示意图。由图可知,二次喷丸后,零件近表层(0~100 μm)内的残余压应力值均比初始状态有所增加,这说明二次喷丸能有效改善零件表层的残余应力场。当二次喷丸速度在50~100 m/s范围内,最大残余压应力随着弹丸速度的增加而增加,表面残余应力和最大残余压应力层深有所波动,残余压应力层深则基本不变。造成这种结果的原因是,二次喷丸强度往往小于一次喷丸强度,二次喷丸对残余应力场的影响主要是增加了近表层的残余压应力值,而对残余压应力层深基本没影响,这也被华程等人[22]的实验结果所证实。弹丸速度为50 m/s和100 m/s的最大残余压应力分别为−823 MPa和−961 MPa,比初始状态提高了4.0%和21.5%。这表明适当提高二次喷丸速度,可获得更大的最大残余压应力。

图4 不同二次喷丸速度下42CrMo钢零件X方向沿层深的残余应力曲线
值得注意的是,当二次喷丸的弹丸速度为50 m/s和60 m/s时,残余应力曲线出现一定的波动。造成这种波动的原因是,二次喷丸使表面残余应力增加的同时,由于内部残余应力需要得到平衡,在零件次表面必然会产生一个拉应力方向的波动。随着二次喷丸弹丸速度的增加,所产生的应力波动的影响深度和一次喷丸的最大残余压应力深度互相重叠,因此当弹丸速度增加到80 m/s以后,残余应力曲线的波动最终消失。
图5为二次喷丸中,弹丸速度为60 m/s,覆盖率为100%,弹丸直径分别为0.3、0.5、0.6、0.8 mm时,42CrMo钢零件方向残余应力沿层深的分布示意图。由图可知,增加二次喷丸直径对残余应力的提高作用并不明显。在零件近表层内,弹丸直径为0.5、0.6、0.8 mm的三条应力曲线基本重叠,这表明残余应力值已趋于饱和。和图4类似,当二次喷丸弹丸直径为0.3、0.5、0.6 mm时,残余应力曲线出现波动,而直径增加到0.8 mm时波动消失。这种波动是一次喷丸和二次喷丸的残余应力内部平衡的结果。增加二次喷丸的弹丸直径后,二次喷丸所产生的应力波动的深度和一次喷丸的最大残余压应力深度重叠,波动最终消失。

图5 不同二次喷丸直径下42CrMo钢零件沿层深的X方向残余应力曲线
图6为二次喷丸中,弹丸速度为60 m/s,直径为0.6 mm,覆盖率分别为50%、100%、200%、300%时,42CrMo钢零件方向残余应力沿层深的分布示意图。由图可知,当二次喷丸覆盖率在50%~300%范围内,增加覆盖率可显著提高零件的表面残余应力,最大可比初始状态提高63.3%。覆盖率为50%时,表面残余应力略微小于初始状态,而当覆盖率为100%和300%时,其表面残余应力分别为−524 MPa和−694 MPa,比初始状态提高了23.3%和63.3%。这表明增加二次喷丸覆盖率对表面残余应力的提高作用最为明显。对比覆盖率为200%和300%的两条应力曲线发现,最大残余压应力分别为−944 MPa和−939 MPa,两者幅值基本相等。这表明覆盖率增大到一定程度后,最大残余压应力值会达到饱和。
3.2 二次喷丸参数对表面粗糙度的影响
经过一次喷丸后,零件表面发生了较大的塑性变形,受喷表面形成的凸峰和凹坑可能会在零件服役中产生应力集中,容易导致微裂纹的萌生,降低喷丸强化效果。二次喷丸的主要目标是提高受喷零件的表面质量,因此还需要考虑二次喷丸参数对表面粗糙度的影响。图7分别为一次喷丸和二次喷丸后42CrMo钢零件的表面形貌示意图。其中一次喷丸参数为= 60 m/s、=1 mm、=100%时,为11.16 μm;而二次喷丸参数为=60 m/s、=0.6 mm、=300%时,为9.55 μm。在该二次喷丸参数下,零件的表面粗糙度与一次喷丸相比有所减小。
图8为不同二次喷丸参数下的42CrMo钢零件表面粗糙度曲线。图中方标为二次喷丸中弹丸直径为0.6 mm,覆盖率为100%,弹丸速度分别为50、60、80、100 m/s时,42CrMo钢零件的表面粗糙度值。由图可知,二次喷丸不一定能降低一次喷丸后零件的表面粗糙度,合理选择二次喷丸参数尤为重要。当速度为50 m/s和60 m/s时,表面粗糙度分别为10.59 μm和10.06 μm,比初始状态分别降低了5.1%和9.9%,零件表面质量得到提升。但当速度增加到80 m/s和100 m/s后,表面粗糙度比初始状态分别增加了15.4%和50.4%,并呈急剧上升的趋势,零件表面变得更粗糙。这表明二次喷丸速度对粗糙度具有显著影响,过度增加二次喷丸速度会导致表面粗糙度显著增加,反而降低零件的表面质量。
图8中圆标为二次喷丸中弹丸速度为60 m/s,覆盖率为100%,弹丸直径分别为0.3、0.5、0.6、0.8mm时,42CrMo钢零件的表面粗糙度值。由图可知,当二次喷丸直径在0.3~0.8 mm范围内,二次喷丸后零件表面粗糙度与初始状态相比均有所降低,降低幅度最大为9.9%。
图8中三角标为二次喷丸中弹丸速度为60 m/s,直径为0.6 mm,覆盖率分别为50%、100%、200%、300%时,42CrMo钢零件的表面粗糙度值。由图可知,提高二次喷丸覆盖率可显著降低表面粗糙度,覆盖率为300%时,粗糙度比初始状态减小了14.4%。当二次喷丸覆盖率在50%~300%范围内时,表面粗糙度随覆盖率的增加而波动。当覆盖率为50%时,表面粗糙度比初始状态增加了12%。而覆盖率为100%、200%和300%时,其粗糙度均小于初始状态,这表明二次喷丸覆盖率大于100%,才有利于表面质量的提升。
3.3 二次喷丸参数对等效塑性形变(PEEQ)的影响
喷丸工艺不仅能在零件表面引入残余压应力,还能使零件表层产生晶粒细化,提高零件的力学性能。研究表明,等效塑性形变(PEEQ)是判断晶粒细化程度的重要指标,PEEQ值越大,则晶粒细化程度越高[23-24]。
图9为二次喷丸中弹丸直径为0.6 mm,覆盖率为100%,弹丸速度分别为50、60、80、100 m/s时,42CrMo钢零件PEEQ值沿层深的变化曲线。由图可知,二次喷丸能显著提高42CrMo钢零件表层区域的PEEQ值,有效改善了零件的等效塑性形变场。当二次喷丸速度在50~100 m/s范围内时,表面PEEQ值和最大PEEQ值随着二次喷丸速度的增加而增加。弹丸速度为50 m/s和100 m/s时,表面PEEQ值比初始状态分别提高了110%和330%,最大PEEQ值分别提高了71%和254%,这表明增加弹丸速度能显著提高PEEQ值。从图中也能看出,随着二次喷丸速度的增加,PEEQ值增加速率逐渐减小,这表明弹丸速度增加到一定程度后,PEEQ值会趋于饱和。
图10为二次喷丸中弹丸速度为60 m/s,覆盖率为100%,弹丸直径分别为0.3、0.5、0.6、0.8 mm时,42CrMo钢零件PEEQ值沿层深的变化曲线。与图9的分析结果相似,表面PEEQ值和最大PEEQ值随二次喷丸直径的增加而增加。当弹丸直径为0.3 mm和0.8 mm时,表面PEEQ值比初始状态分别提高了135%和160%,最大PEEQ值分别提高了79%和129%。同样地,随着二次喷丸弹丸直径的增加,PEEQ值逐渐趋于饱和。

图10 不同二次喷丸直径下42CrMo钢零件沿层深的PEEQ曲线
图11为二次喷丸中弹丸速度为60 m/s,直径为0.6 mm,覆盖率分别为50%、100%、200%、300%时,42CrMo钢零件PEEQ值沿层深的变化曲线。由图可知,增加二次喷丸覆盖率对PEEQ值的改善作用最为显著,覆盖率为300%时,表面PEEQ值和最大PEEQ值分别比初始状态提高了615%和461%。当二次喷丸覆盖率为100%、200%和300%时,表面PEEQ值和最大PEEQ值随二次喷丸覆盖率的增加而增加,PEEQ的增加速率则随覆盖率的增加而逐渐减小。

图11 不同二次喷丸覆盖率下42CrMo钢零件沿层深的PEEQ曲线
4 结论
1)二次喷丸后,42CrMo钢零件近表层(0~ 100 μm)残余压应力值均比初始状态有所增加。增加二次喷丸覆盖率对表面残余应力的提高作用最为明显,最大可比初始状态提高63.3%。增加二次喷丸直径对残余应力的改善效果最不明显。
2)过度增加二次喷丸速度会导致42CrMo钢零件表面粗糙度显著增加。提高二次喷丸覆盖率可显著降低表面粗糙度,覆盖率为300%时,粗糙度比初始状态减小了14.4%。
3)42CrMo钢零件表层PEEQ值随着二次喷丸速度、弹丸直径和覆盖率的增加而增加,但当二次喷丸速度、弹丸直径和覆盖率增加到一定程度后,表层PEEQ值会趋于饱和。
[1] KOBAYASHI M, MATSUI T, MURAKAMI Y. Mechanism of creation of compressive residual stress by shot peening[J]. Nihon Kikai Gakkai Ronbunshu, A Hen/Transactions of the Japan Society of Mechanical Engineers, Part A, 1998, 20(5): 351-357.
[2] TORRES M A S, VOORWALD H J C. An evaluation of shot peening, residual stress and stress relaxation on the fatigue life of AISI 4340 steel[J]. International journal of fatigue, 2002, 24(8): 877-886.
[3] HU Dian-yin, GAO Ye, MENG Fan-chao, et al. A unifying approach in simulating the shot peening process using a 3D random representative volume finite element model[J]. Chinese journal of aeronautics, 2017, 30(4): 1592.
[4] UNAL O, VAROL R. Surface severe plastic deformation of AISI 304 via conventional shot peening, severe shot peening and repeening[J]. Applied surface science, 2015, 351: 289-295.
[5] INÉS F P, MARIO G. About the role of residual stresses and surface work hardening on fatigue Δthof a nitrided and shot peened low-alloy steel[J]. Surface and coatings technology, 2008, 202(13): 3072-3080.
[6] 赵西洋, 陈晓秀, 孟海英. 喷丸强化技术在某型作动筒延寿修理中的应用[J].装备环境工程, 2018, 15(12): 87-90. ZHAO Xi-yang, CHEN Xiao-xiu, MENG Hai-ying. Application of shot peening technology on lifetime extension repair of an actuator cylinder[J]. Equipment environmental engineering, 2018, 15(12): 87-90.
[7] HARDING M D, DONALDSON I W, HEXEMER R L, et al. Characterization of the microstructure, mechanical properties, and shot peening response of an industrially processed Al-Zn-Mg-Cu PM alloy[J]. Journal of materials processing technology, 2015, 221: 31-39.
[8] BAGHERIFARD S, GHELICHI R, GUAGLIANO M. A numerical model of severe shot peening (SSP) to predict the generation of a nanostructured surface layer of material[J]. Surface and coatings technology, 2010, 204(24): 4081-4090.
[9] MIAO H Y, LAROSE S, PERRON C, et al. On the potential applications of a 3D random finite element model for the simulation of shot peening[J]. Advances in engineering software, 2009, 40(10): 1023-1038.
[10] HONG T, OOI J Y, SHAW B. A numerical simulation to relate the shot peening parameters to the induced residual stresses[J]. Engineering failure analysis, 2008, 15(8): 1097- 1110.
[11] 梁若, 解丽静, 庞思勤. 34CrNiMo6钢复合喷丸强化的有限元模拟[J]. 航空制造技术, 2017, 60(10): 99-103. LIANG Ruo, XIE Li-jing, PANG Si-qin. Finite element simulation of 34CrNiMo6 steel after dual shot peening[J]. Aeronautical manufacturing technology, 2017, 60(10): 99- 103.
[12] 赵莉莉, 王建明, 裴信超. 喷丸残余应力场有限元数值模拟分析[J]. 材料保护, 2015(1): 6-7. ZHAO Li-li, WANG Jian-ming, PEI Xin-chao. Finite element simulation of residual stress field after shot peening[J]. Materials protection, 2015(1): 6-7.
[13] GANG W, ZHOU W, JIN G, et al. FE analysis of shot- peening-induced residual stresses of AISI 304 stainless steel by considering mesh density and friction coefficient[J]. Surface engineering, 2018, 1-13: 242-254.
[14] KIRK D, ABYANEH M Y. Theoretical basis of shot peening coverage control[J]. The shot peener, 1993, 2(9): 28-30.
[15] BAGHERIFARD S, GHELICHI R, GUAGLIANO M. On the shot peening surface coverage and its assessment by means of finite element simulation: A critical review and some original developments[J]. Applied surface science, 2012, 259: 186-194.
[16] HOLZAPFEL H, SCHULZE V, VÖHRINGER O, et al. Residual stress relaxation in an AISI 4140 steel due to quasistatic and cyclic loading at higher temperatures[J]. Materials science & engineering A, 1998, 248(1-2): 9-18.
[17] MENIG R, SCHULZE V, VÖHRINGER O. Optimized warm peening of the quenched and tempered steel AISI 4140[J]. Materials science & engineering A, 2002, 335(1-2): 198- 206.
[18] KLEMENZ M. Anwendung der simulation der randschichtausbildung beim kugelstrahlen auf die abschätzung der schwingfestigkeit gekerbter bauteile[D]. Karlsruhe: Karlsruhe University, 2009.
[19] MACHERAUCH E, MÜLLER P. Das sin2ψ-verfahren derröntgenographischen spannungsmessung[J]. Z angew phys, 1961, 13: 340-345.
[20] NOYAN I C, COHEN J B. Residual stress-measurement by diffraction and interpretation[M]. New York: Springer Verlg, 1987.
[21] MOORE M G, EVANS W P. Mathematical correction for stress in removed layers in X-ray diffraction RS analysis[J]. SAE trans, 1958, 66: 340-345.
[22] 华程, 姚兰, 李国庆, 等. 复合喷丸强化对A-100钢旋转弯曲疲劳寿命的影响[J]. 中国表面工程, 2019, 32(2): 137-142. HUA Cheng, YAO Lan, LI Guo-qing, et al. Effects of double shot peening on rotational bending fatigue life of A-100 steel[J]. China surface engineering, 2019, 32(2): 137-142.
[23] HUANG H, WANG Z, GAN J, et al. The study of universality of a method for predicting surface nanocrystallization after high energy shot peening based on finite element analysis[J]. Surface and coatings technology, 2019, 358: 617-627.
[24] UMEMOTO M, TODAKA Y, TSUCHIYA K. Formation of nanocrystalline structure in steels by air blast shot peening[J]. Materials transactions, 2003, 44: 1488-1493.
Numerical Simulation on Surface Integrity of 42CrMo Steel after Dual Shot Peening
1,1,2,1,1,1,1
(1.a. School of Automotive Engineering, b. Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology, Wuhan 430070, China; 2.School of Transportation, Wuhan University of Technology, Wuhan 430063, China)
The work aims to explore the influence of dual shot peening parameters on the surface integrity of 42CrMo steel components. A 3D random shot peening (SP) finite element model (FEM) was established and the accuracy of predicting the residual stress by the model was verified by experimental data. The surface topography and stress-strain results of the component after single shot peening were imported into the dual shot peening model as the initial state, to construct the prediction model of dual shot peening. The effects of the dual shot peening parameters on the surface residual stress field, surface roughness and equivalent plastic deformation (PEEQ) field of 42CrMo steel components were analyzed. The compressive residual stress value near the surface layer (0~100 μm) of 42CrMo steel components after dual shot peening increased compared with the initial state, and the dual shot peening coverage ratio had the most obvious effect on the improvement of the surface residual stress, with the maximum increase of 63.3% compared with the initial state. On the contrary, the improvement effect of dual shot peening diameter on residual stress was the least obvious. The excessive increase of the dual shot peening speed would lead to the significant increase of the surface roughness while the increase of the dual shot peening coverage ratio could significantly reduce the surface roughness, and the roughness was 14.4% less than the initial state when the coverage ratio was 300%. The surface PEEQ value ascended with the increase of the dual shot peening speed, shot diameter and coverage ratio. However, when the shot speed, shot diameter and coverage ratio increased to a certain extent, the PEEQ value tended to be saturated. The prediction model of dual shot peening reveals the relationship between dual shot peening parameters and surface integrity of 42CrMo steel component, which provides some guidance for the industrial application of dual shot peening.
dual shot peening; numerical simulation; surface integrity; residual stress; equivalent plastic deformation; surface roughness
2019-12-09;
2020-05-08
HE Jia-xi (1995—), Male, Master, Research focus: lightweight of automobile, multiphysics coupling simulation.
汪舟(1981—),男,博士,副教授,主要研究方向为汽车轻量化、汽车零部件先进制造、多物理场耦合仿真。邮箱:wangzhou@whut.edu.cn
Corresponding author:WANG Zhou (1981—), Male, Doctor, Associate professor, Research focus: lightweight of automobile, advanced manufacturing of auto parts, multiphysics coupling simulation. E-mail: wangzhou@whut.edu.cn
何嘉禧, 汪舟, 甘进, 等. 二次喷丸42CrMo 钢表面完整性的数值模拟研究[J]. 表面技术, 2020, 49(6): 216-223.
2019-12-09;
2020-05-08
国家自然科学基金(51405356,51772228)
Fund:Supported by the National Natural Science Foundation of China (51405356, 51772228)
何嘉禧(1995—),男,硕士研究生,主要研究方向为汽车轻量化、多物理场耦合仿真。
TG668
A
1001-3660(2020)06-0216-08
10.16490/j.cnki.issn.1001-3660.2020.06.026
HE Jia-xi, WANG Zhou, GAN Jin, et al. Numerical simulation on surface integrity of 42CrMo steel after dual shot peening[J]. Surfacetechnology, 2020, 49(6): 216-223.

