基于SWAT模型与Copula修正的融雪径流模拟

邢贞相，金超群，纪 毅，付 强，刘 东

（东北农业大学水利与土木工程学院，哈尔滨 150030）

受温度季节性变化影响，中高纬度地区积雪融化为典型自然现象，其产生的融雪径流是融雪季节径流重要组成部分，也是河流主要补给来源。在全球变暖背景下，全球范围内积雪正在逐渐消融[1]，积雪融水变化对当地供水、防洪、灌溉和雪崩等生态环境和生产生活具有重要影响[2]。因此，模拟融雪径流对流域内水资源持续利用具有现实意义[3]。

融雪过程受温度、辐射、土地覆盖等自然因素影响[4]。融雪径流模拟采用两类方法，一类方法基于温度指数法，假设温度是融雪主要影响因子，另一类是能量平衡法，考虑所在流域内能量交换[5-6]。目前，全球已开发多个带有融雪模块分布式水文模型，如VIC、UEB、DHSVM和SWAT等，可对融雪径流作精准模拟[7-8]。

温度指数方法由于输入参数较少、模型计算简单等特点应用广泛[9-10]。Marks等研究表明，雨夹雪天气产生融雪对空气与积雪间能量交换最敏感[11]，温度指数方法忽略风速等自然因素作用，低估融雪前和融雪季节融雪。能量平衡方法在融雪模拟中综合考虑多因素条件影响。当一定温度与高湿度和风速共同作用时，显热和潜热成为能量主要来源，导致积雪开始融化[12]。Fontaine等认为能量平衡方法需额外气象和地形参数输入[13]。孟现勇等研究表明，在无额外数据要求情况下，能量平衡方法在融雪预测中表现优于温度指数方法[14]。Fuka等将不同形式能量平衡方法嵌入SWAT模型中[15]。Zhang等使用3种融雪模型应用于大型山区流域（中国黄河上游水域）发现，能量平衡方法性能优于温度指数方法[16]。Debele等发现模拟3个不同流域（美国两个小流域和中国黄河一个大流域）日径流量方面[12]，能量平衡方法不如温度指数方法。因模拟3个流域时，能量平衡方法中校准参数始终保持不变。针对不同流域环境应分别校准。为提高融雪径流模拟精度，Piani等提出利用数理统计方法预测模拟后误差[17]，寻找模拟值与其误差间相关性并修正模拟值。

为保证融雪径流模拟精度，本文利用分布式SWAT模型模拟我国东北地区三江平原挠力河流域融雪期（3～5月）内径流，采用Copula函数预报径流模拟误差，修正径流模拟值提高模拟精度，为流域春季农业灌溉用水配置及春季防汛抗旱提供参考。

1 研究方法

1.1 SWAT融雪模块

SWAT融雪模块采用温度指数法模拟融雪过程[13]。当日平均气温低于SWAT参数（SFTMP），将降水视为雪。当日平均气温高于SWAT参数（SMTMP）时，积雪开始融化。则雪水当量平衡计算方程为：

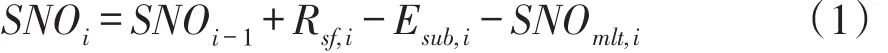
式中，SNOi和SNOi-1分别是第i天和第i-1天雪水当量；Rsf,i是第i天降雪量；Esub,i是蒸发量；SNOmlt,i是融雪量。

积雪温度随着气温变化而变化，主要受前1 d平均积雪温度影响。前日积雪温度对今日积雪温度影响可用滞后系数（TIMP）描述。该参数用于解释积雪密度、湿度和阳光。积雪温度计算如下:

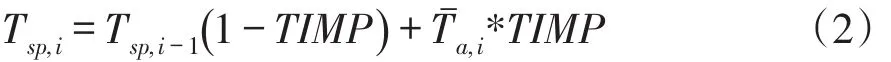
式中，Tsp,i和Tsp,i-1分别为第i天和第i-1天积雪温度；Ta,i平均气温。则融雪量计算如下:

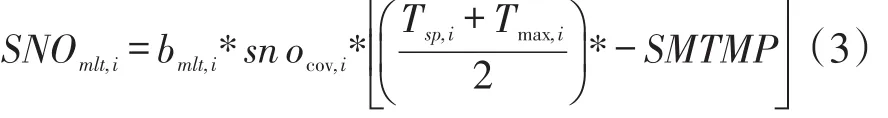
其中，Tmax为最高气温；bmlt,i为第i天融雪系数其计算如下:

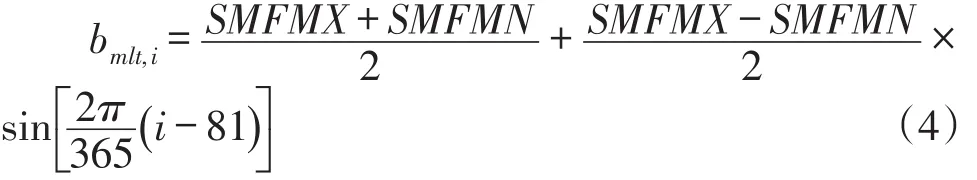
式（4）中，SMFMX和SMFMN分别为最大值和最小值融雪因子。

1.2 二维Copula函数表达式

Copula函数克服传统多变量联合分布要求边际分布为同一类型分布不足，通常水文模型模拟值与其误差间具有相关关系，提高水文模型模拟精度，本文在率定期采用Copula函数描述模拟值和误差值联合概率分布，探讨两者关系，预报误差修正模拟值。

在众多Copula家族中，阿基米德Copula在水文研究应用广泛。阿基米德Copula中以Clayton Copula、Gumbel Copula和Frank Copula 3个函数应用最广。其中，Frank Copula结构简单，描述对称相关结构，对正负相关性均可适用且不限制相关性程度，而其他两种Copula函数仅适用于正相关水文序列[18]。

本文研究融雪径流及其模拟误差序列关系不一定为正相关，因此选择Frank Copula作为联合分布函数，构建融雪径流及其模拟误差联合分布。

在Copula理论中，具有不同边缘分布变量X和Y联合分布函数表示为式（5）:

式中，H（x,y）为联合分布函数；C（·，·）为连接2个边缘概率分布Copula函数；F（x）和G（y）分别是x，y边缘概率分布，若F、G连续，则C唯一。

Frank Copula函数作为Copula成员之一，最早由Frank于1979年提出，表达式为式（6）：

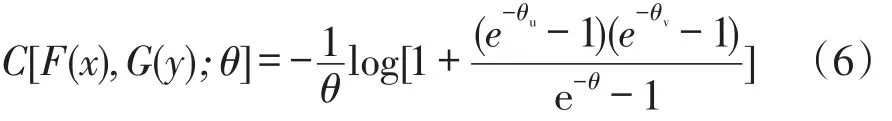
式中，u和v分别为变量边缘累积概率；θ为参数，其取值范围为-∞＜θ＜+∞，可由Kendall秩相关系数τ求得，而τ与θ表达式为式（7）和（8）为：

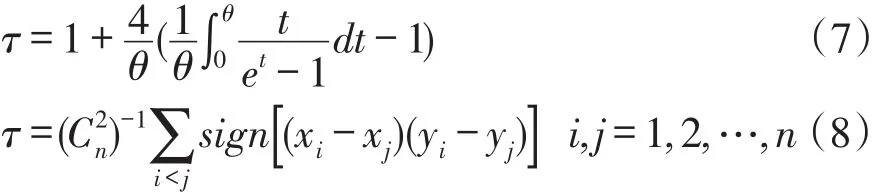
式中，（xi,yi）为样本数据，sign为signum函数。

1.3 误差修正方案

在传统水文模拟中，利用多年历史水文数据率定一组固定模型参数，代入水文模型，用于模拟验证期水文过程。由于模型输入误差、结构不完善及参数不确定性，导致模拟值存在不同程度误差。

1.3.1 Copula修正

为降低模拟值误差，本文采用Copula函数描述模拟径流值与误差值联合概率分布，揭示两者关系，并通过预报误差以修正模拟值，减小模拟误差，达到提高模拟精度目的，此方法在文中称为Copula修正。

本文将2004～2008年作为率定期（2004年为模型预热期），将该时期数据作为此率定模型参数值，并构建模拟值及其误差相关关系。具体步骤为：首先，将DEM、土地利用、土壤数据、气象数据输入SWAT模型中，模拟融雪期（3～5月）日径流。计算径流模拟值与实测值误差，并确定误差值与模拟值概率分布、计算两变量间Kendall相关系数（τ），确定 Frank Copula参数（θ）值，建立Frank Copula联合概率分布函数。将2009～2014年作为验证期（2009年为模型预热期），利用已率定模型参数，模拟融雪期径流，采用Coupla修正方法修正模拟值。

1.3.2 优化处理

采用滑动平均法平滑修正后得到最终模拟值，本文将该方法称为优化处理。优化处理基于统计规律，将连续数据定义为一个长度固定为N序列，在新数据加入时，去掉该序列首个数据，其余N-1个数据依次前移，在第N个位置插入新数据，形成新序列，并对新序列作均值运算处理，将运算结果作为本次测量值，依次类推[19]。该方法在本文中主要用于修正后径流过程线平滑。

2 应用实例

2.1 研究区域

挠力河流域（如图1）位于中国黑龙江省三江平原东北部（东经45°43′～47°35′，北纬131°21′～134°10′），流域以东南部完达山为界，东接乌苏里江，流域总面积2.42×104km2；挠力河流域地处寒温带大陆性湿润季风气候区，年平均气温2.3～3.4℃。流域内河流一般在11月中旬结冰，次年3月初解冻。年降雪量30～150 mm，其融雪径流占全年径流总量13.3%～24.9%。

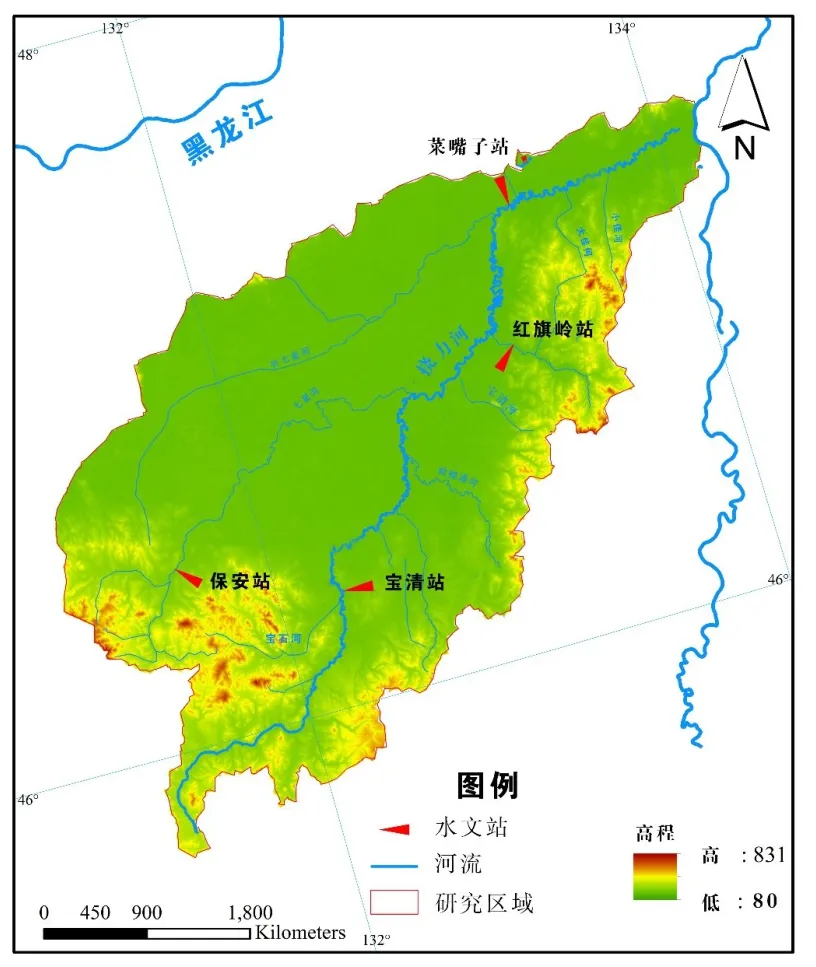
图1 挠力河流域概况Fig.1 General map of Naoli River Basin

2.2 数据

SWAT模型主要输入数据包括数字高程模型（DEM）、土地利用、土壤属性和日气象数据（降水、最高和最低气温、相对湿度、风速和太阳辐射）。本研究数据来源于网上公开数据，部分数据来自黑龙江省水文年鉴，来源如表1所示。

2009年颁布的《中华人民共和国邮政法》中为快件损坏赔偿问题提供了法律依据。根据新邮政法的相关规定，普遍邮政服务业务范围以外的邮件的损失赔偿，适用有关民事法律的规定，并明确要求快递企业应当在其营业场所公示或者以其他方式公布其损失赔偿办法，以及用户对其服务质量的投诉办法，以保障公众的知情权。“快递企业要加强对消费者合法权益的保护，今后可以采取保价、保险的方法解决赔偿问题，即用户根据寄递物的贵重程度，选择办理相应的保价业务，如发生丢失或损毁，由快递企业依据保价金额进行赔偿。”

表1 研究数据来源Table 1 Research data source

2.2.1 数字高程模型

数字高程模型（DEM）在流域和子流域所有地形属性数据集推导过程中发挥重要作用，其属性包括面积、坡度、坡度长度等，本文采用分辨率为30 m DEM作为输入数据集。

SWAT输入包括1个最小值-80 m和最大值831 m数字高程模型（DEM）。流域主要地形为平原，主要分布于流域中北部，坡度在0～5°。山区分布在流域西部和南部，大部分山区坡度在9°以上。

2.2.2 土地使用

采用2012年土地利用地图，其原始空间分辨率为30 m。轻微修改原数据与SWAT数据库一致，主要包括农用地（80.17%）、林地（17.37%）和其他土地用途包括草、水、城市（2.46%）。

2.2.3 土壤类型与特征

根据土壤科学数据库定义不同土壤类别，可以查询我国主要土壤类型、面积、分类名称和典型剖面分布情况，确定研究流域14种土壤类型，主要包括普通淋溶土（22.24%）、薄层黑土（18.41%）、松软潜育土（17.89%），而其余11种类型土壤平均占总流域面积3.8%。

2.2.4 气象和径流数据

2.3 模型设置与配置

运用SWAT模型模拟研究流域内水量平衡，DEM对流域划分是模拟过程中第一步。在流域划分后，定义水文响应单元（HRUs），HRUs是地形、土地利用和土壤类型相似区域，下垫面特征相对单一和均匀，具有相似水文特征。因此，3个空间数据集（坡度、土地利用和土壤属性）对于HRUs定义具有重要意义。将所需气象变量输入至模型，包括降雨量、最低和最高温度、相对湿度、平均风速和太阳辐射数据。应用SWAT模型模拟。在模型启动过程中，将2004～2008年作为率定期，确定适用于此流域参数值。而2009～2014年作为验证期，评估模型适用性，其中2004、2009年则分别作为模型在相应时段的热身期，在模型模拟过程中仅模拟融雪期（3～5月）日径流。

3 结果与分析

3.1 模型率定

SWAT-CUP广泛用于SWAT校准计算机程序，作为SWAT操作重要补充，SWAT-CUP工具提供5种SWAT验证方法，即GLUE、Para Sol、SUFI2、MCMC和PSO算法。李倩楠等比较5种不确定性评价方法，认为SUFI-2方法运行次数少、运算效率高[21]，故本研究采用SUFI2标定方法，并根据SWAT输入/输出文档中参数特征、物理特征和参数范围确定挠力河流域SWAT模型参数。选用参数及其描述、调整下限和上限见表2。

选用纳什效率系数（NSE）、确定性系数（R2）、平均绝对误差（MAE）及均方根误差（RMSE）作为模型评价指标。利用NSE及R2作为本文主要评价方法，估计模型参数适用性，而MAE与RMSE对比相同时段不同模拟方法结果。NSE＞0.5，R2＞0.6，且MAE与RMSE均小于30，模拟效果显著。本文率定期（2004～2008年）内每年融雪期日径流模拟值与实测值对比见图2。模型评价结果见表3。可见，效率系数仅0.26，2008年融雪期径流峰值小于其他年份，这是SWAT模拟径流不准原因，但整体模拟效果良好，故SWAT模型在挠力河流域融雪径流模拟中具有良好适用性。

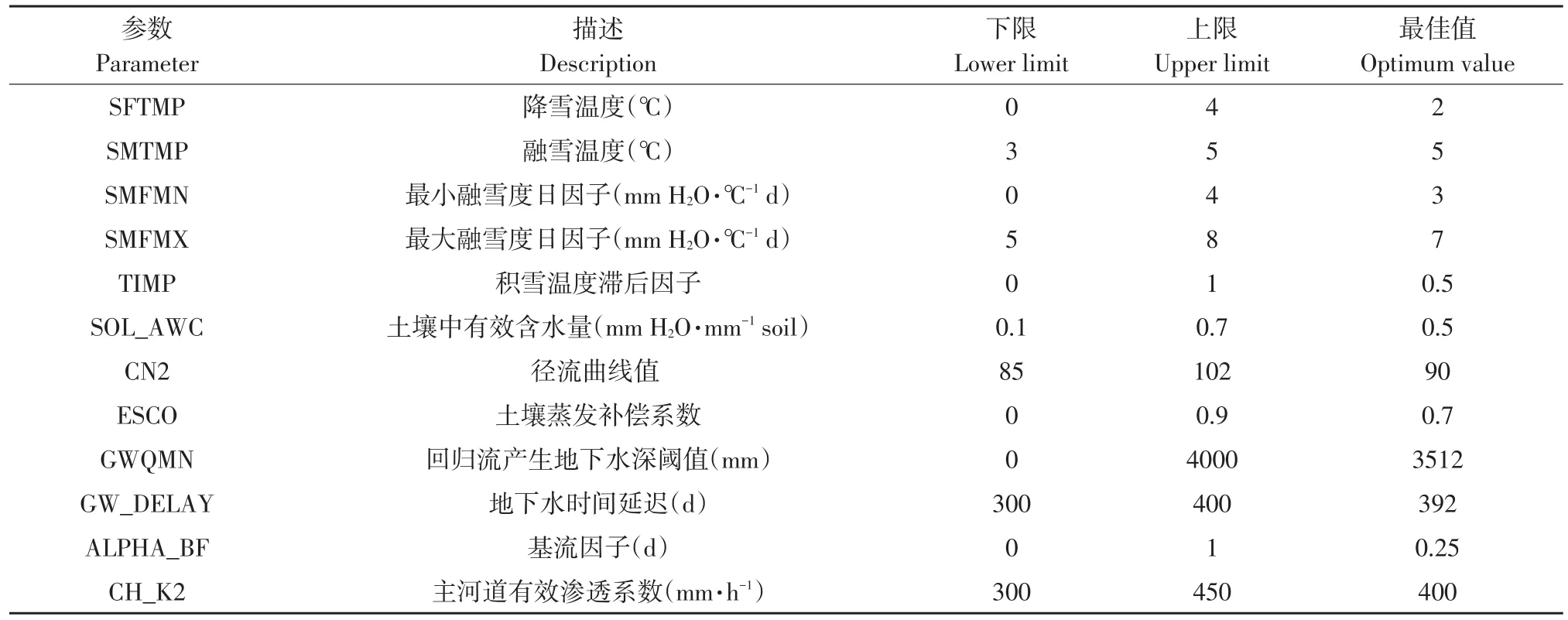
表2 挠力河流域SWAT模型参数率定值Table 2 Calibration of SWAT model parameters in the Naoli River basin

图2 率定期（2005～2008）径流过程线Fig.2 Runoff process line in the calibration(2005-2008)

表3 率定期（2005～2008）模拟结果Table 3 Result of simulation in the calibration(2005-2008)

3.2 参数敏感性分析

本文采用SWAT-CUP中全局敏感性分析[22]，利用t值和P值评价模型参数敏感性。参数敏感性与t值呈正相关、与P值呈负相关，结果如图3所示，CN2和ALPHA_BF其t值均在4～5，其中CN2的t值大于ALPHA_BF，P值均接近于0，故在研究区域中参数敏感性CN2排名第一，ALPHA_BF排名第二。而SFTMP、SMTMP和TIMP其t值均在1.5～2.5，P值均在0～0.4。而其他参数t值均小于1.5，P值则在0.4以上。综上所述，在12个参数中，CN2和ALPHA_BF是最敏感参数，其次为SFTMP、SMTMP和TIMP。

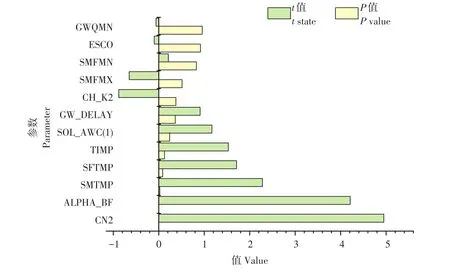
图3 参数敏感性关系Fig.3 Relation diagram of parameter sensitivity

3.3 基于Copula验证期模拟修正

由表3可知，率定期参数值（即由参数确定模型）对2006年径流模拟精度较高，2008年较差。但整体上，率定期模型模拟精度良好。为提高个别年份及整体模拟精度，本文利用Frank Copula对模拟径流值与误差值建立联合概率分布，用于融雪期模拟径流Copula修正。由图2可知，前期融雪期径值流较低，模拟精度较高，修正必要性不大，因此本文仅对自融雪期开始第40天后径流模拟值作Copula修正。利用非线性拟合技术确定模拟径流值及误差值概率分布（见图4），其中图4a、b分别为模拟值和误差值概率分布。本文对模拟值分别采用韦伯分布、正态分布和伽马分布作拟合尝试，而对误差值采用正态分布、极值分布和Logistic分布作拟合尝试。拟合结果发现，正态分布对模拟值和误差值拟合效果良好，其中模拟径流值主要分布在30～60，而误差主要分布在5～25。利用Cop⁃ula函数对两者联合概率分布描述见图5。

图4 模拟径流值与误差值概率密度分布Fig.4 Probability density distribution of simulated runoff values and error values

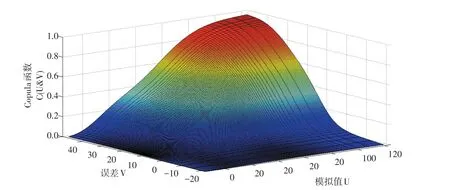
图5 误差V和模拟值U联合概率分布Fig.5 Joint probability distribution of errors and simulation values

构建SWAT模拟验证期（2010～2014年）融雪期径流，采用Copula修正并经优化处理，融雪径流模拟结果如表4所示，模拟径流过程如图6所示。由表4可知，验证期SWAT模拟纳什效率系数值为0.75，采用Copula修正方法纳什效率系数为0.92，利用移动平均法优化处理纳什效率系数为0.93。对于确定性系数、平均绝对误差和均方根误差，与传统SWAT模型相比，经Copula修正和优化处理后验证期整体模拟结果均有明显提高，单一年份模拟结果也有所提高（2014年NSE提高139%）。然而，2012年Copula修正后较SWAT模拟结果有所降低（NSE降低22.5%），但优化处理后模拟结果提高且与SWAT模拟相当。由2012年SWAT模拟径流过程可知，SWAT模拟径流值远大于真实值。但在率定期，SWAT模拟值低于真实值，Copula修正后无理想结果，但优化处理后可弥补。综上所述，经修正处理后，融雪期日径流模拟精度有明显改善。

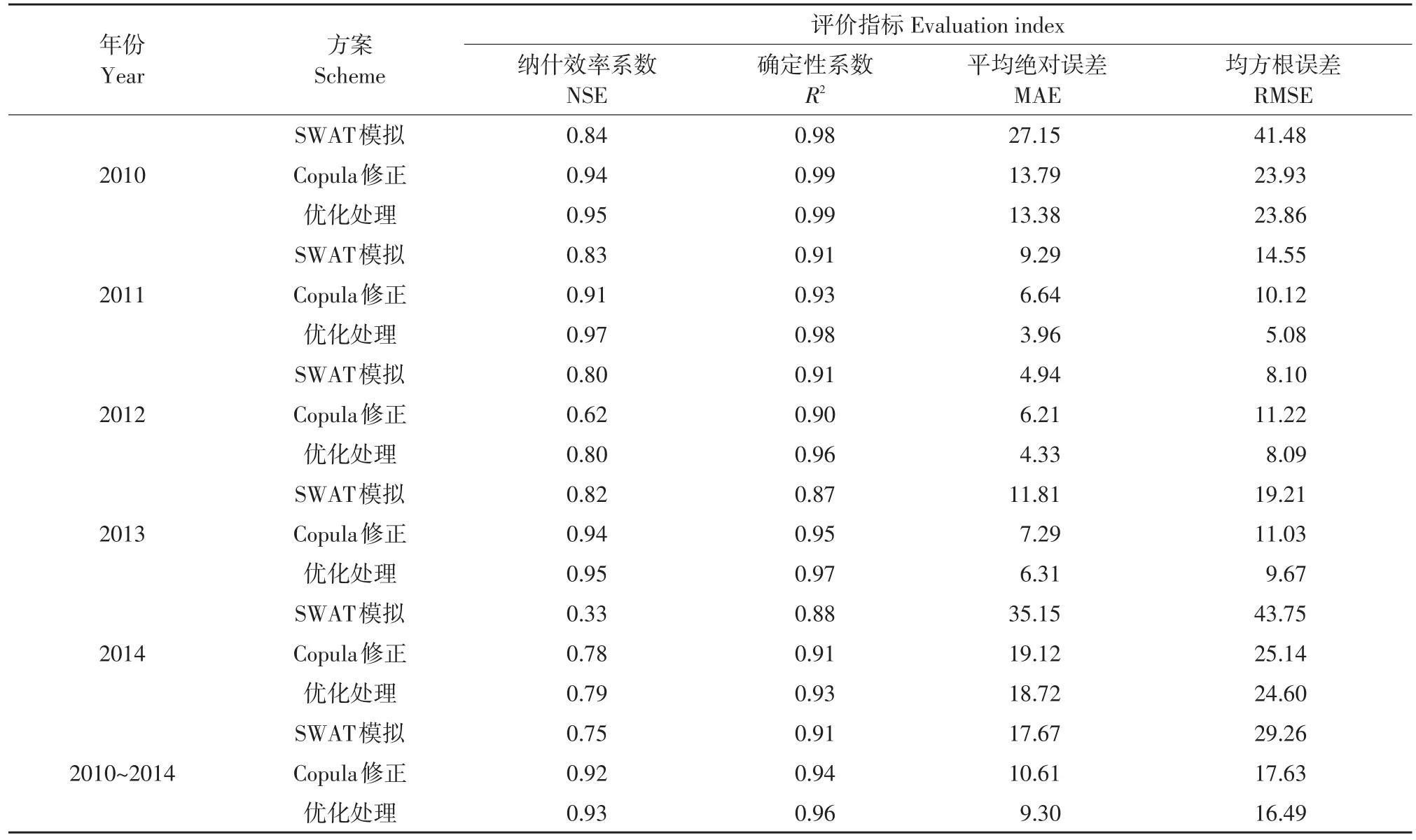
表4 验证期模型模拟结果、修正结果及优化处理结果Table 4 Results of the simulation,correction and optimization in the validation

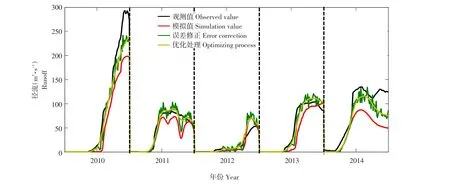
图6 验证期模型模拟、修正及优化处理径流过程Fig.6 Runoff process of the simulation,correction and optimization in the validation

4 讨论与结论

通过敏感性分析发现，CN2（径流曲线数）和ALPHA_BF（基流系数）为主要敏感参数（敏感程度分列1～2位），并与控制地表径流和地下径流密切相关。CN2取决于土地利用类型和土壤含水量，而ALPHA_BF主要控制地下径流量，因SWAT模型模拟融雪径流在计算过程中主要通过影响地表径流与地下水补给控制河道径流量。与融雪有关参数（SMTMP、SFTMP和TIMP）分别排在 3～5位。其中，SMTMP是融雪温度，为模拟融雪径流重要参数。在SWAT融雪模块中，当平均气温达到SMT⁃MP值时，雪开始融化。SFTMP是降雪温度。在融雪期前几个月，由于气温较低，大量降水以雪形式储存在流域中。评价融雪期前以雪形式储存水量在径流模拟中具有重要作用。因此，SFTMP在模型模拟中与SMTMP有重要作用。积雪温度受前1 d积雪平均温度影响极大，随气温升降而变化。前日积雪温度对今日积雪温度影响可用滞后因子描述。因素由TIMP指定，TIMP是集总参数，综合考虑积雪密度、含水量和日照等因素，灵敏度较高。在SWAT模型中，由于模拟融雪径流采用温度指数法，温度相关参数灵敏度处于中等水平。

模拟结果分析发现，无论是率定期还是验证期均采用同一套模型参数，对有些年份模拟精度较好，但个别年份模拟精度不理想，如2008和2014年，其纳什效率系数分别为0.26和0.33。原因是在模拟过程中模型参数存在不确定性。

本文提出Copula修正和优化处理并未改变SWAT模型融雪径流计算方法，仅修正和处理模拟结果，提高模型模拟精度。通过图2和6发现，SWAT模拟径流值低于实测值，因SWAT融雪径流模拟采用是温度指数法，未考虑融雪期风速对融雪影响。Copula修正和优化处理方法可弥补SWAT模型不足。通过验证期模拟径流过程（图6）发现，修正后径流过程线并非平滑曲线，利用滑动平均法对Copula修正后径流作平滑优化处理。由表4发现，2010～2014年Copula修正后纳什效率系数为0.92，优化处理后纳什效率系数为0.93，模拟精度提高。优化处理方法可平滑Copula修正过程线，提高径流模拟精度。