波浪滑翔器水下牵引机滑翔动力分析

孙秀军, 王力伟, 桑宏强

波浪滑翔器水下牵引机滑翔动力分析

孙秀军1,2,3, 王力伟2, 桑宏强4

(1. 河北工业大学 机械工程学院, 天津, 300130; 2. 中国海洋大学 物理海洋教育部重点实验室, 山东 青岛, 266100; 3. 青岛海洋与技术试点国家实验室, 山东 青岛, 266237; 4. 天津工业大学 机械工程学院, 天津, 300387)

波浪滑翔器的纵向速度与水下牵引机结构参数有很大关系, 其中水下牵引机自重和水翼最大俯仰角对其影响尤为突出。文中以“海哨兵”波浪滑翔器为研究对象, 采用牛顿-欧拉方程建立水翼动力学模型, 对最优自重及最优角度进行计算流体力学仿真, 并将仿真结果与试验数据进行对比分析。分析结果可知, 受到多种因素的影响, 两者数据存在一定偏差, 但两者总体趋势相近, 数据显示20°俯仰角为水翼的最优俯仰角, 3级海况条件下, 45 kg的自重使得水下牵引机在下滑时间和下滑位移方面更加匹配波浪特性。文中在部分参数确定的情况下, 研究自重和俯仰角对波浪滑翔器推进效率的影响, 可为波浪滑翔器后续的参数优化和设计提供参考。

水下牵引机; 水翼; 波浪滑翔器; 自重; 俯仰角

0 引言

波浪滑翔器是一种能够将波浪能转化为前向动能的水面无人航行器, 具有工作时间长、位置自主可控等优点, 可广泛应用于水文气象观测、水质生态调查、卫星遥感验证以及水面通信中继等领域[1-3]。当前, 如何提升波浪滑翔器的运动速度逐渐成为该领域的研究焦点之一。提升波浪滑翔器的运动速度也就是提高波浪滑翔器的波浪动力转化效率。波浪动力转化效率主要取决于波浪滑翔器的双体结构参数以及水下牵引机的结构参数等。对于水下牵引机来说, 其自重、翼板翼型和翼板弹簧机构等参数选择, 以及不同参数的组合对波浪转化效率都会产生不同程度的影响, 在各个参数相互耦合的关系中, 找出波浪动力转化效率的优化路线以及完成耦合参数的优选, 对波浪滑翔器的运动速度提升至关重要。

刘鹏等[4]基于雷诺平均(Reynolds average Navier-Stockes, RANS)方程利用二维面元法计算了摆幅角、翼间距及升沉幅度等因素对水下牵引机推进性能的影响, 并给出小翼间距可产生更大推力的结论。Yang等[5]基于URANS方程利用计算流体力学(computational fluid dynamics, CFD)软件FINE/Marine与STAR-CCM+联合仿真了波浪滑翔器整个运动周期。Caiti等[6]利用拉格朗日方法对波浪滑翔器纵垂面进行建模分析, 求解了总体位移和速度与时间的对应关系。贾立娟[7]利用Kane方法对波浪滑翔器进行动力学建模, 分析了波浪滑翔器水下牵引机升阻比的影响因素。但上述研究主要集中在理论层面, 尚未在工程设计中给出水下牵引机细节机构的参数选择依据, 例如, 水下牵引机自重、弹簧劲度系数、水翼限位轴与转动轴的距离等与推进效率的对应关系。

文中以“海哨兵”波浪滑翔器的牵引机结构为研究对象, 在相关结构参数确定的情况下分析水下牵引机自重与波浪滑翔器滑翔效率的对应关系, 找到已有结构下水下牵引机的最优自重, 进而确定最优俯仰角。最后, 对波浪滑翔器的实际滑翔效率进行了试验, 在趋势上验证了理论分析、流体仿真和真实情况之间的一致性。

1 结构组成及工作原理

波浪滑翔器是由水面浮体船、柔性铠装缆、水下牵引机组成的双体结构系统。水面浮体船在波浪的作用下产生上下起伏运动, 通过柔性铠装缆拉拽水下牵引机上下运动, 受迫垂向运动的水下牵引机水翼与水质点发生相对滑翔运动, 水质点对水翼产生前向作用力, 水下牵引机产生向前运动, 反之, 水下牵引机通过柔性铠装缆带动水面浮体船前向运动, 其运动过程如图1所示。

图1 波浪滑翔器运动原理

为便于求解水下牵引机滑翔效率, 做出如下假设: 1) 波浪滑翔器的垂向运动完全符合波浪周期, 且为周期性正弦运动; 2) 以6对水翼代表整个水下牵引机, 不考虑水下牵引机其余部件的水动力影响; 3) 水下牵引机向下滑落时水翼保持最大滑翔角的时间为整个波浪周期的1/5, 下落位移为波高的1/2, 此状态下水下牵引机在水中处于自由落体状态, 柔性铠装缆对水下牵引机不施加外力作用。

根据波浪滑翔器运动特性, 其水翼的运动规律如图2所示。

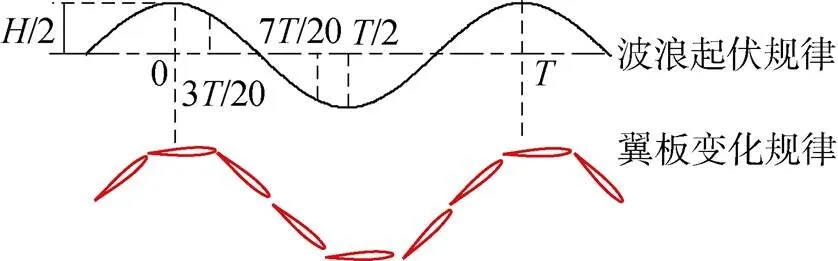
图2 水翼运动曲线

2 数值模型

2.1 动力学模型

水翼受力情况如图3和图4所示, 利用牛顿-欧拉方程[8]建立水翼下滑过程中纵向速度、垂向速度的动力学模型, 用以揭示水翼运动与自重和俯仰角的特征关系, 水翼动力学方程的显式表达形式为

式中:为水翼质量; d为仿真时间步长;为弹簧与水平方向夹角;为水动力合力;为水动力合力与水平方向夹角;为水翼重力;为水翼绕轴旋转的角加速度;L为水翼相对于质心方向的转动惯量;F、F分别为在、方向上的分力;F为弹簧拉力, 由于文中着重研究水翼处于最大俯仰角的状态, 此状态下, 弹簧与水翼的相对状态不变, 弹簧拉力为恒定值。

图3和图4中:为水翼攻角;为水翼俯仰角;1为弹簧拉拽点与质心的水平距离;2为旋转轴与限位轴的距离;3为旋转轴与质心的距离。

图3 水翼下滑受力情况示意图

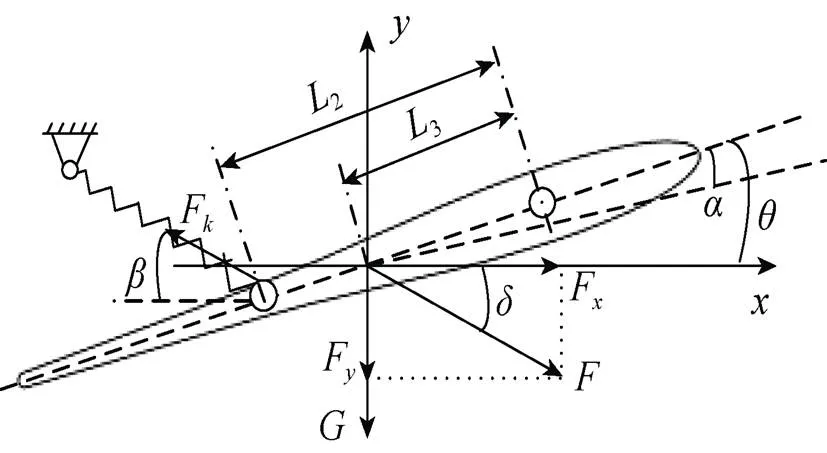
图4 水翼上滑受力情况示意图

文中由于水翼下滑时间1, 垂向位移≤1,因此, 水下牵引机水翼的最优方程可以表达为式(2), 式中相关参数均由“海哨兵”波浪滑翔器已有数据测得, 其几何参数及动力学参数如表1所示。

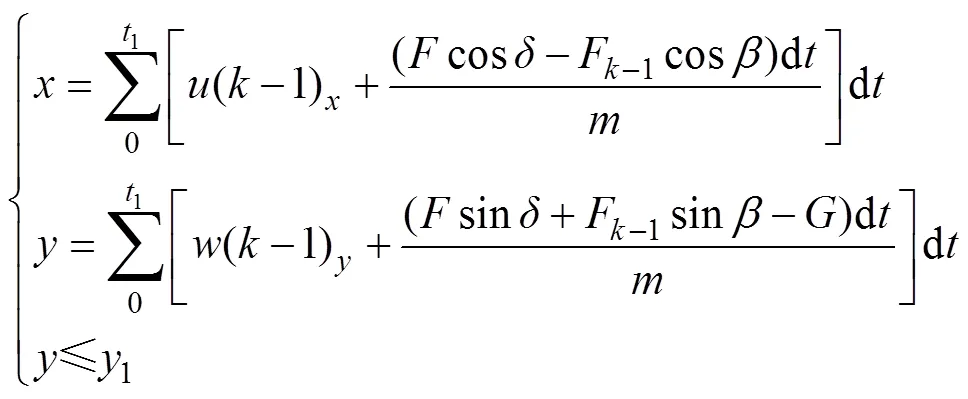
表1 波浪滑翔器几何参数及动力学参数

2.2 仿真模型及参数

文中采用类NACA0012翼型[9]单对水翼进行仿真, 水翼特征弦长=0.16 m, 质心位置由SolidWorks确定并使之与原点重合, 利用CFD计算软件FLUENT对二维水翼进行仿真, 仿真模型计算域为15×20,为水翼弦长, 左边界和上边界距离翼型质心的距离均为5, 全局网格采用非结构性网格, 边界层为10层, 并严格控制第1层网格高度+值小于60, 如图5所示。

图5 模型边界及水翼近壁网格

2.3 网格无关性验证

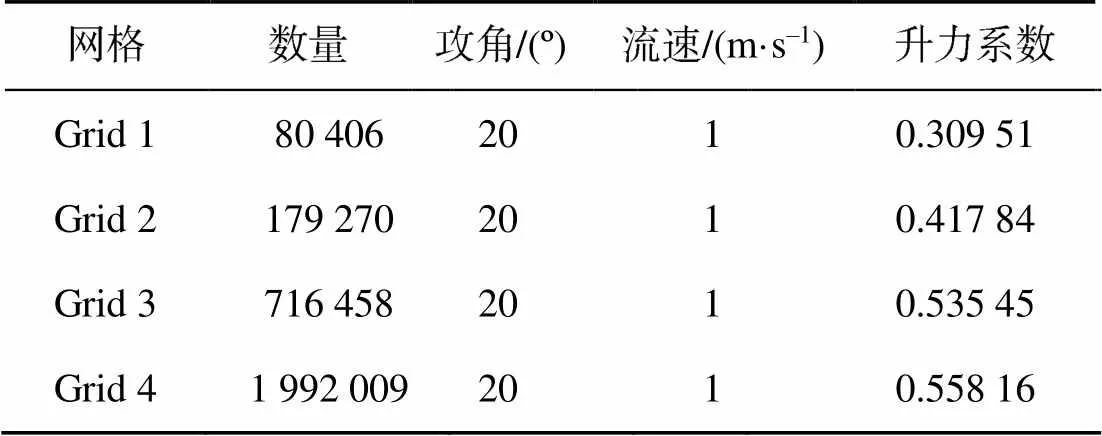
表2 FLUENT网格无关性验证

3 数值计算仿真与分析

太平洋海况波谱如表3所示[10], 据表显示太平洋中3级海况最为常见, 由于海况的复杂性和不确定性增加了对海浪系统性仿真的难度, 因此拟采用太平洋中最常见的3级海况进行仿真以达到简化的效果。

表3 太平洋海况波谱

利用6自由度动网格方法对水翼20°俯仰角下5~9 kg不同水翼质量进行仿真[11], 得到水翼纵向速度曲线见图6。从图中可知, 当水翼质量为2 kg时, 在初始的一段时间内由于自身质量较轻, 水翼尾缘分流效果作用明显, 导致其存在非稳状态: 水翼纵向速度达到约0.7 m/s后, 其运动状态逐渐稳定, 且在0.25 s下滑时间内, 该质量水翼的纵向速度远超其余情况纵向速度; 当下滑时间较大时, 该质量水翼运动状态趋于稳定, 纵向加速度较小, 纵向速度小于其余质量水翼的纵向速度。5~9 kg水翼的纵向运动较为相似, 纵向速度随着质量的增加而增加。

图6 不同质量水翼纵向速度随时间变化曲线

图7给出了水翼的纵向位移曲线, 从图中可以看出, 7.5 kg水翼更加吻合假定3)中关于下滑时间和下滑位移的设定, 因此将45 kg(7.5 kg×6)质量视为水下牵引机最优自重进行下一步仿真。

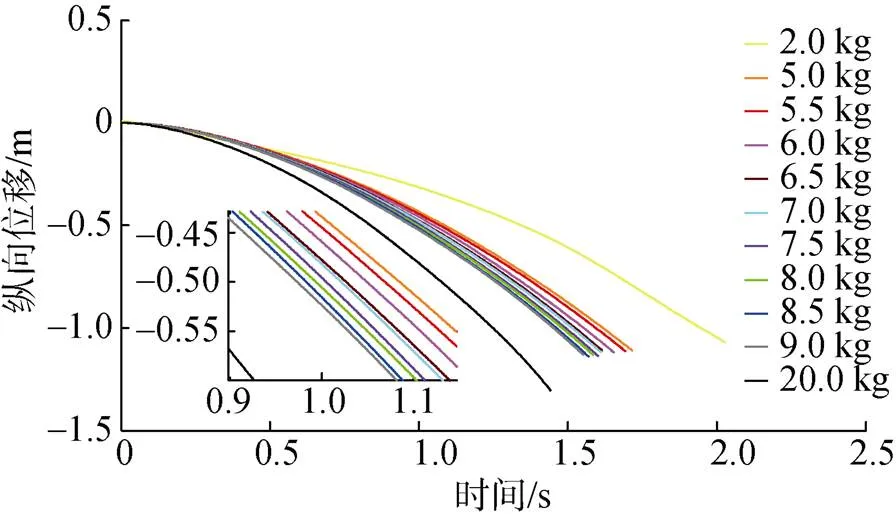
图7 不同质量水翼纵向位移随时间变化曲线

在最优自重情况下, 分别对10°、15°、20°和25°俯仰角的纵向位移和下滑时间进行仿真, 其结果如图8和图9所示。从图中可以看出, 当水翼俯仰角在10°~20°范围内时, 其纵向位移随着俯仰角的增大而增大; 在20°时达到峰值; 当水翼俯仰角为25°时, 其纵向位移在初始一段时间内较大, 但由于其俯仰角较大导致升力系数减小, 该俯仰角度的水翼在后续时间的纵向速度小于其他水翼。

图8 不同俯仰角水翼纵向位移随时间变化曲线

图9 不同俯仰角水翼纵向速度随时间变化曲线

根据仿真数据绘得1 s时间内不同俯仰角的水翼纵向位移曲线, 如图10所示。可以看出, 相同下滑时间时, 20°俯仰角有较大纵向位移; 当俯仰角为25°时, 水翼的纵向位移逐渐减小, 因此认为20°为水下牵引机在最优自重情况下的最优俯仰角。

图10 1 s滑翔时间内水翼纵向位移随俯仰角变化仿真曲线

4 水池试验与数据对比分析

4.1 水池试验

为验证仿真数据的准确性, 现利用一定机构进行水池试验验证, 其结构如图11所示。定滑轮将水下牵引机固定在一定高度, 利用单一变量法将水下牵引机的结构参数根据仿真条件进行相关调整, 具体试验结构参数如表4所示。将水下牵引机在水中自由释放, 观察记录水下牵引机垂向位移0.5 m所需时间及其下滑的纵向位移。图12为水下牵引机水池试验现场照片。

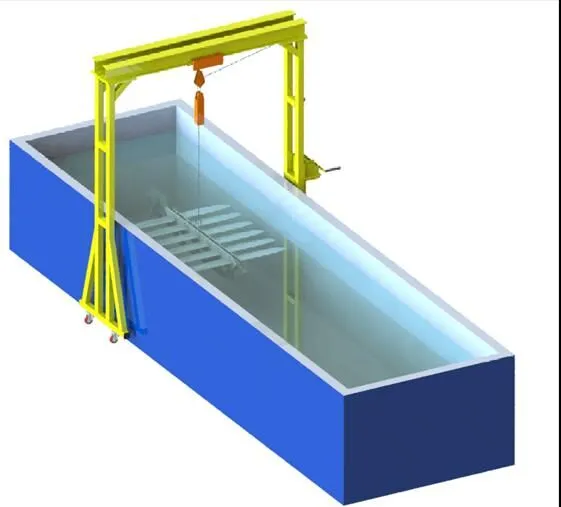
图11 水下牵引机水池试验装置结构图

表4 水下牵引机试验结构参数

图12 水下牵引机水池试验

4.2 数据对比分析

由于试验装置的局限性, 并未对2 kg和20 kg翼重对应的水下牵引机自重进行试验, 利用去最值平均法对每组参数测得的数据进行处理, 将处理后的数据与仿真数据进行对比, 其结果如图13~图16所示。

图13 20°俯仰角下仿真与试验纵向位移对比曲线

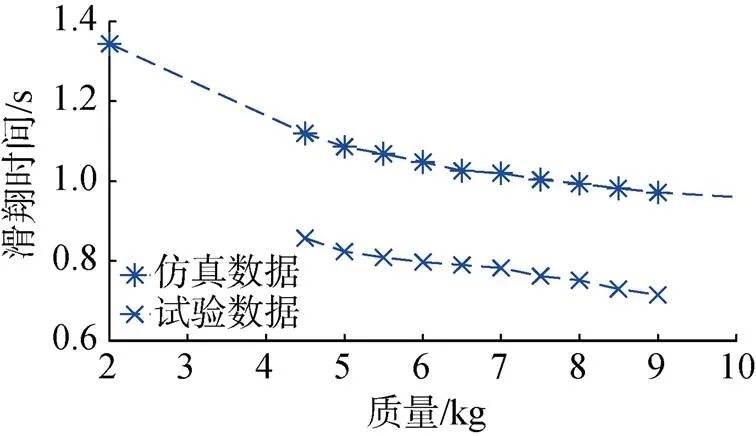
图14 20°俯仰角下仿真与试验时间对比曲线

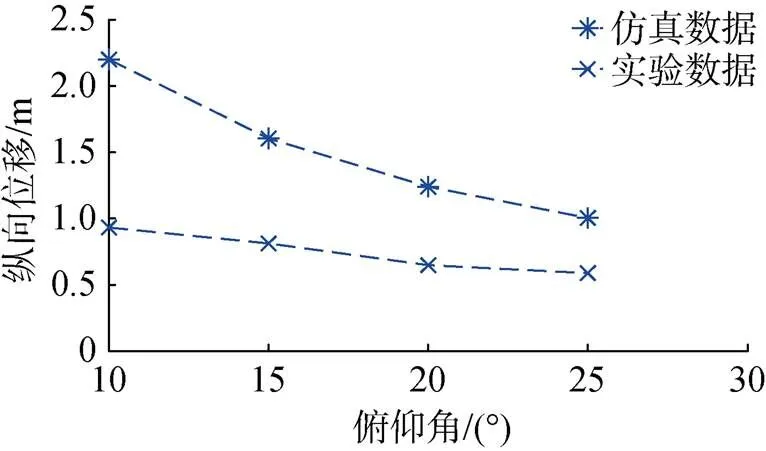
图15 7.5 kg质量下仿真与试验纵向位移对比曲线

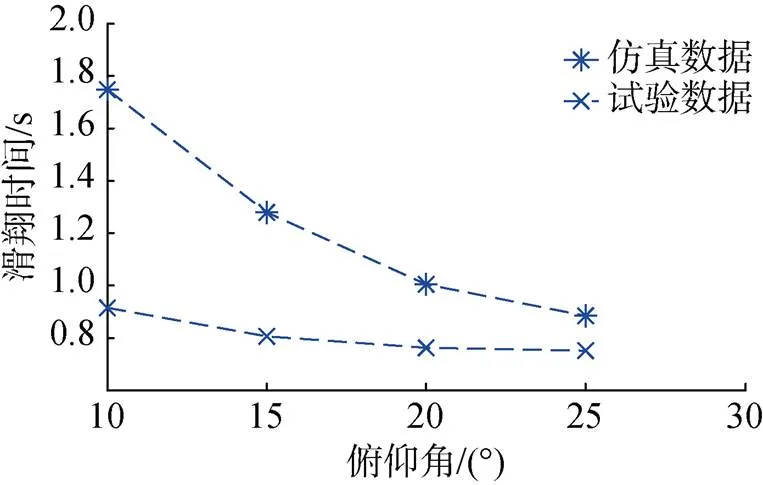
图16 7.5 kg质量下仿真与试验时间对比曲线

从图中可以看出, 试验数据与仿真数据存在一定偏差, 分析存在如下原因。

1) 试验过程中数据测量存在误差。

2) 水池试验装置的边界效应明显, 运动过程中边界扰流作用较大, 导致水下牵引机运动与仿真存在一定偏差。

3) 仿真模型与实际试验设备存在出入, 试验模型中除水翼之外存在其余部件, 试验过程中其余部件水阻力导致水下牵引机的试验数据与仿真数据存在差别。

4) 仿真模型为单对水翼, 实际试验模型为6对水翼, 水翼之间的流场扰动导致水翼实际受力与仿真存在偏差。

5 结束语

由于上文所述原因, 仿真数据和试验数据存在一定出入, 但两者总体趋势相近。

该文仅考虑了水下牵引机对波浪滑翔器纵向速度的影响, 但在实际工作中, 波浪滑翔器的工作性能是水面浮体船和水下牵引机多种因素耦合产生的结果, 在今后的研究中将尽量向实际情况靠拢, 以便更真实的分析其影响因素。此外在数据测量准确性方面仍有提升空间。

[1] Daniel T, Manley J, Trenaman N. The Wave Glider: Enabling a New Approach to Persistent Ocean Observation and Research[J]. Ocean Dynamics, 2011, 61(10): 1509- 1520.

[2] Goebel N L, Frolov S, Edwards C A. Complementary Use of Wave Glider and Satellite Measurements: Description of Spatial Decorrelation Scales in Chla Fluorescence Across the Pacific Basin[J]. Methods in Oceanography, 2014, 10: 90-103.

[3] 廖煜雷, 李晔, 刘涛, 等. 波浪滑翔器技术的回顾与展望[J]. 哈尔滨工程大学学报, 2016, 37(9): 1227-1236.Liao Yu-lei, Li Ye, Liu Tao, et al. Unmanned Wave Glider Technology: State of the Art and Perspective[J]. Journal of Harbin Engineering University, 2016, 37(9): 1227- 1236.

[4] 刘鹏, 苏玉民, 刘焕兴, 等. 串列异步拍动翼推进性能分析[J]. 上海交通大学学报, 2014, 48(4): 457-463.Liu Peng, Su Yu-min, Liu Huan-xing, et al. Propulsive Performance Analysis of Tandem Asynchronous Flapping Foil[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 457-463.

[5] Yang F M, Shi W C, Zhou X, et al. Numerical Investigation of a Wave Glider in Head Seas[J]. Ocean Engineering, 2018, 164: 127-138.

[6] Caiti A, Calabro V, Grammatico S, et al. Lagrangian Mo- deling of the Underwater Wave Glider[C]//OCEANS 2011. Spain: IEEE, 2011: 1-6.

[7] 贾立娟. 波浪动力滑翔机双体结构工作机理与动力学行为研究[D]. 天津: 国家海洋技术中心, 2014.

[8] Smith R, Das J, Hine G, et al. Predicting Wave Glider Sp- eed from Environmental Measurements[C]//Oceans 2011. Waikoloa, HI ,USA: IEEE, 2011: 1-8.

[9] Yousefi K, Saleh R. Three-dimensional Suction Flow Control and Suction Jet Length Optimization of NACA 0012 Wing[J]. Meccanica, 2015(6): 1481-1494.

[10] 付诚翔. 波浪滑翔器的浮体阻力及运动性能分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.

[11] 桑宏强, 李灿, 孙秀军. 波浪滑翔器纵向速度与波浪参数定量分析[J]. 水下无人系统学报, 2018, 26(1): 16-22.Sang Hong-qiang, Li Chan, Sun Xiu-jun. Quantitative An- alysis on Longitudinal Velocity and Wave Parameter of Wave Glider[J]. Journal of Unmanned Undersea Systems, 2018, 26(1): 16-22.

1. 孙芹东, 兰世泉, 王超, 等. 水下声学滑翔机研究进展及关键技术[J]. 水下无人系统学报, 2020, 28(1).

2. 桑宏强, 游宇嵩, 孙秀军. 波浪滑翔器网络版岸基监控中心设计[J]. 水下无人系统学报, 2019, 27(5).

3. 孙秀军, 王雷, 桑宏强. Petrel-Ⅱ 200水下滑翔机动力学建模及仿真[J]. 水下无人系统学报, 2019, 27(5).

4. 王冠琳, 王岩峰, 官晟. 水下滑翔机数据管理[J]. 水下无人系统学报, 2019, 27(5).

5. 吴尚尚, 李阁阁, 兰世泉, 等. 水下滑翔机导航技术发展现状与展望[J]. 水下无人系统学报, 2019, 27(5).

6. 尹云龙, 杨明, 杨绍琼, 等. 基于水下滑翔机的海洋声学背景场观测技术[J].水下无人系统学报, 2019, 27(5).

7. 孙秀军, 王雷, 桑宏强. “黑珍珠”波浪滑翔器南海台风观测应用[J]. 水下无人系统学报, 2019, 27(5).

8. 钱洪宝, 卢晓亭. 我国水下滑翔机技术发展建议与思考[J]. 水下无人系统学报, 2019, 27(5).

9.刘来连, 闵强利, 张光明. “海鲟4000”水下滑翔机水动力特性与滑翔性能研究[J]. 水下无人系统学报, 2019, 27(5).

10. 桑宏强, 李灿, 孙秀军. 波浪滑翔器纵向速度与波浪参数定量分析[J]. 水下无人系统学报, 2018, 26(1).

11. 孙春亚, 宋保维, 王鹏. 翼身融合水下滑翔机外形优化设计[J]. 水下无人系统学报, 2017, 25(2).

Gliding Dynamics Analysis for Underwater Tractor of Wave Glider

SUNXiu-jun1,2,3, WANGLi-wei1, SANGHong-qiang4

(1. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China; 2. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China; 3. Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China; 4. School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300387, China)

The longitudinal velocity of wave glider is closely related to the structural parameters of the underwater tractor, especially, the self-weight of the underwater tractor and the maximum pitch angle of the hydrofoil are crucial. In this study, a dynamic model of the hydrofoil of the Sea Sentry wave glider was established by using the Newton-Euler equations to simulate the optimum weight of the underwater tractor and the optimum pitch angle of the hydrofoil in computational fluid dynamics(CFD) simulation software. Furthermore, the simulation results were compared with the test data. Due to the influence of various factors, there is a certain deviation between the two kinds of data, but the general trends are similar, and the data show that 20° pitch angle is the optimal pitch angle of hydrofoil. Under the level three sea condition, the self-weight of 45 kg can make the underwater tractor more suitable for wave characteristics in terms of gliding time and gliding displacement. The effects of the weight and pitch angle on propulsion efficiency were studied under the condition that some parameters were fixed, which provided reference for the subsequent parameter optimization and design of wave glider.

underwater tractor; hydrofoil; wave glider; self-weight; pitch angle

U674.941; O353.2

A

2096-3920(2020)03-0252-07

10.11993/j.issn.2096-3920.2020.03.002

2019-10-11;

2019-11-19.

国家重点研发计划重点专项(2017YFC0305902); 青岛海洋科学与技术国家实验室“问海计划”项目(2017WHZZB 0101); 天津市自然科学基金重点基金(18JCZDJC40100).

孙秀军(1981-), 男, 教授, 硕导, 主要研究方向为海洋移动观测平台技术.

孙秀军, 王力伟, 桑宏强. 波浪滑翔器水下牵引机滑翔动力分析[J]. 水下无人系统学报, 2020, 28(1): 252-258.

(责任编辑: 杨力军)