高产气井瞬时关井对油管内流体流动的影响

张智，王嘉伟，李炎军，罗鸣，张超

（1.西南石油大学油气藏地质及开发工程国家重点实验室，成都 610500；2.中海石油（中国）有限公司湛江分公司，广东湛江 524057）

0 引言

随着高温、高压、高产气井不断投入开发，开采难度不断增大，对井筒完整性提出了更高的要求[1-5]。尤其是高产气井（无阻流量大于120×104m3/d）在开采过程中，受地质和油管条件等因素影响，产量随时间一直波动，且常面临开关井工况[6-7]。高产气井产量高，流速快，开关井速度对油管压力分布影响较大。开关井速度过快将导致较大的波动压力，诱发严重的井筒完整性问题[8]；而开关井速度过慢，则开关井操作时间过长，会对现场作业造成较大的影响。1981年10月4日，德州一口气井发生井喷，事故原因主要是开关井速度过快形成水锤产生高压所致[9]。四川盆地东北部的河坝 1井试采初期因关井过快严重影响了气井的正常生产，甚至出现天然气爆泄险情[10]。因此，研究开关井时油管内的瞬变流动过程、根据实际生产优化开关井时间对保障井筒完整性至关重要。

油管内的流动可看作是非恒定有压管流，在这种流态下，若流体流速骤然发生改变，会在油管内产生剧烈的压力波动[11]。气井生产中，采气树阀门开度发生变化时，油管内流体的速度随之发生改变，进而产生波动压力。开度变化的急缓影响波动压力的大小，当阀门急骤地启闭时，油管内的波动压力可能达到正常压力的数倍甚至数十倍，且压力的反复变化会引起油管和设备的振动，严重时会造成油管及井口装置的损坏[12]而引发事故，影响井筒的完整性及安全生产。

阀门瞬关产生的波动压力也被称作水锤。水锤现象表现出了流体的可压缩性，是一个瞬变流问题，它体现出流体在运动过程中，流域内的所有运动物理量（速度、压力等）兼具时变与位变的性质。目前，水锤问题得到国内外学者的高度重视，该问题已成为流体力学瞬变流领域内一大研究焦点。1993年Jardine等[13]提出了“硬关井”与“软关井”问题，并指出了硬、软关井操作的优劣。Erika等[14]预测了气井内流体在充填过程中的瞬态现象。Jalal等[15]研究了一种微压缩宾汉流体的流动，建立了基于水平井压力和压力导数的新解析方程，并对6种不同工况进行了逐步计算验证。国内学者对油管内流体瞬变过程的研究更多体现在钻井过程中。何世明等[16]用ADINA软件对溢流关井产生的波动压力进行了有限元仿真研究。彭齐等[17]以槽流模型为基础，结合起下钻过程中的流体真实速度分布情况，分别讨论了层流、紊流状态下的波动压力，建立了基于钻柱运动的稳态井筒波动压力计算模型。陈林等[18]提出了压力波速标准图版的绘制方法并绘制了压力波速图版，用以查询油管气液两相流在不同温压和含水率下的压力波速。

尽管对水锤的相关研究取得了众多成果，但在气井采气阶段，有关气井瞬变流的研究均未讨论阀门开度系数、持液率等参数对油管内压力的影响，同时油管造斜段部分流体瞬变流动情况研究的报道也很少。因此，建立适用于气井复杂工况的瞬变流模型，并对油管造斜段进行单独建模，分析讨论阀门开度系数、持液率等参数对油管流体瞬态流动的影响很有必要。本文针对该问题，建立适用于气井多相流环境的瞬变流数学模型，并对油管的造斜部分单独进行建模，分析关井工况对油管内流体瞬变流动的影响，为研究油管内实际流动过程及气井压力分布[19-20]提供技术支持。

1 气井瞬变流动数学模型

1.1 气井关井瞬变流动过程

气井油管内的瞬变流动过程与普通管道类似，完成一次压力的传递需要经历4个阶段（一个周期）。设井深为L，压力传播速度为cm，井口流速为u0，井口压力为p0，那么一次压力传递分为 4个阶段：①0～L/cm；②L/cm～2L/cm；②2L/cm～3L/cm；④3L/cm～4L/cm。

在井口阀门关闭的瞬间，紧贴阀门高度为Δz的微元流体速度会立刻变为0，流动满足实际流体总流的伯努利方程。若从截面A1到A2定义一段元流（见图1），由元流积分成总流，则可得实际流体总流的伯努利方程，如（1）式所示。

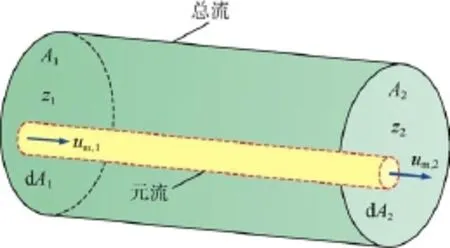
图1 实际流管流体元流示意图

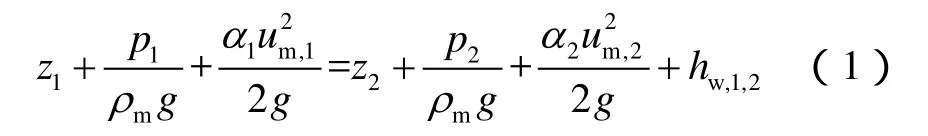
该方程确立了实际流体总流流动中的势能与动能、流速与压强相互转化的普遍规律。若取高度为Δz的微元流体作为研究对象，位置水头和沿程摩阻就可以忽略不计，即该微元流体的速度水头和压力水头之和为一定值。速度减小，压力必然增大。

图2为气井形成水锤过程的4个阶段。井口阀门关闭后，压力波以波速cm向井底传播，经过t=L/cm后传播到井底；油管内流体压力为p0+Δp（Δp=Δp1+Δp2+…+Δpi）。此时，油管内压力高于井底，靠近井底流体以速度um,0向井底倒流，上方流体依次流入井底。在L/cm～2L/cm内，压差逐渐消失并恢复到常压。当t=2L/cm时，流体在重力的作用下仍以速度um,0向井底流动，油管内产生负压，形成减压波面并以波速cm向井底传播，直至压力降为p0−Δp。当t=3L/cm时，井底压力高于油管内压力，流体以速度um,0向上运动，井底的流体压力恢复到p0。这种不平衡依次以波速cm向井口传播，在t=4L/cm时传到井口。至此，气井关井产生的水锤压力完成了一个周期的传播。

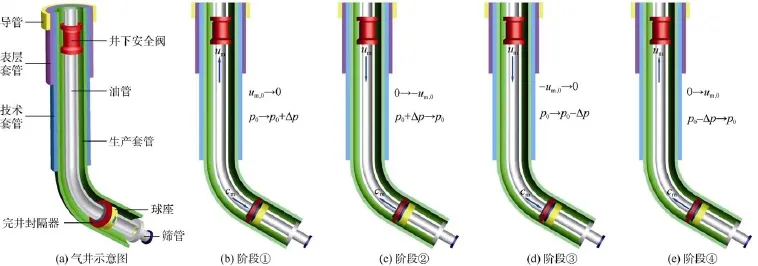
图2 气井形成水锤的压力波动传播过程

1.2 气井瞬变流控制方程

经典瞬变流模型研究的是水平管道单相流，而且大多数仅考虑了液相。井下环境复杂多变，需要考虑诸多经典模型中未考虑到的因素：在垂直或近似垂直的油管中，经典模型无法准确地描述重力带来的影响；在造斜段，需考虑流体冲击弯头受到的反弹性膨胀力与该段因急变流造成的局部摩阻；油管中的传播介质是多相流体[21-22]，压力波速与流体流速等参数会因相的增加发生很大的变化。无论是钻井过程还是生产过程，此时单相流模型都无法满足计算需求。

考虑多相流后，会涉及到油管内流动介质相间的相互作用，介质物性受体积比、密度比等参数的影响，以及十分复杂的流型转变和相间质量、动量、能量传递过程等。因此，在建模时需作简化：①油管内的流动介质与油管壁均为线弹性体，弹性模量恒定，油管纵向无弹性形变；②油管内的流动介质为一元流动，沿油管同一截面上的多相流体分布均匀，流速相同；③瞬变流中摩阻计算仍沿用油管恒定流公式。

研究油管内瞬变流动过程的基础是瞬变流动基本微分方程组。该微分方程组由连续性方程和运动方程构成。如图 3所示，于直井段和造斜段各取一有限长度（弧度）的流体段作为研究对象，长度（弧度）为dz，流体进口节点为j，流体出口节点为j+1。

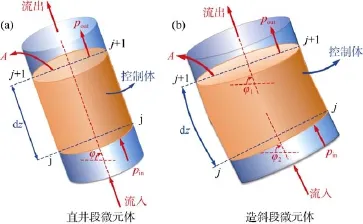
图3 油管有限单元的流入与流出

因为直井段与造斜段不影响流体的连续介质假设，故两种井段条件下采用同一连续性方程。根据所取有限元控制体在dt时间段内的质量守恒关系，有：

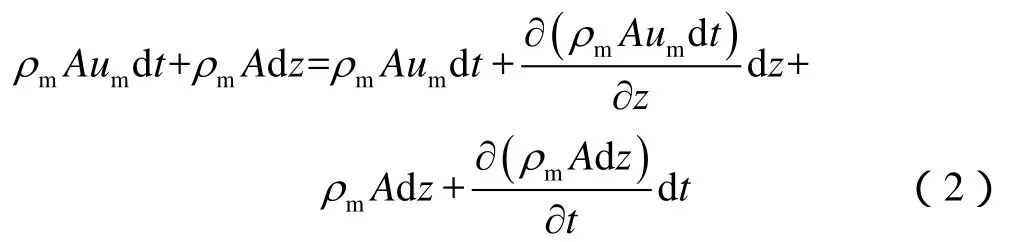
简化整理可得：

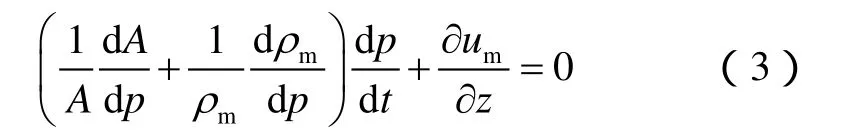
在考虑多相流因素的分析中，达西公式失效，此时摩擦阻力需要通过范宁摩阻公式进行计算：

那么相应的水锤压力可表达为：

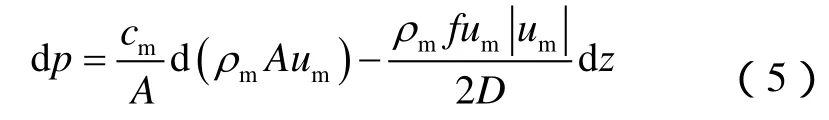
这里的cm是多相流条件下的压力波速（此处不考虑固相），定义为：

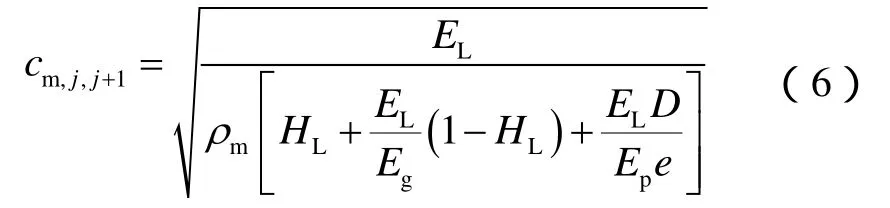
在油管材料、尺寸确定后，如忽略油管内气液流体弹性模量的变化，则持液率的改变会直接影响压力波速，从而影响该截面的水锤压力。根据上式，持液率减小，压力波速会增加，从而导致水锤压力的增加。

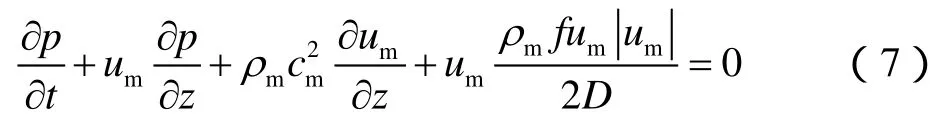
由此可得到描述气井瞬变流过程的连续方程为：同样，于直井段和造斜段各取一有限长度（弧度）的流体段作为研究对象，长度（弧度）为dz，流体进口节点为j，流体出口节点为j+1，受力分析如图4所示。

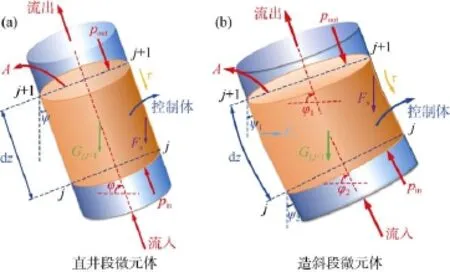
图4 油管有限单元的受力分析

当流体混合物流过直井段时，根据以上的受力分析，可以得到该段所受的合力为：

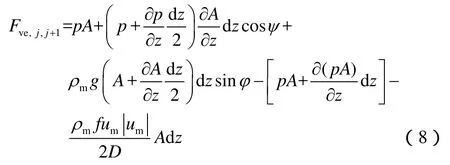
当流体混合物流过油管造斜段时，由于惯性作用，流体会冲击弯头处，假设管壁为线弹性体，故会反作用给流体一个弹性膨胀力：

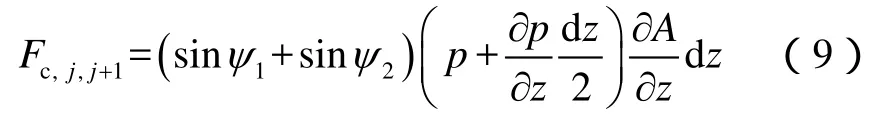
此时，造斜段所受的合力为：

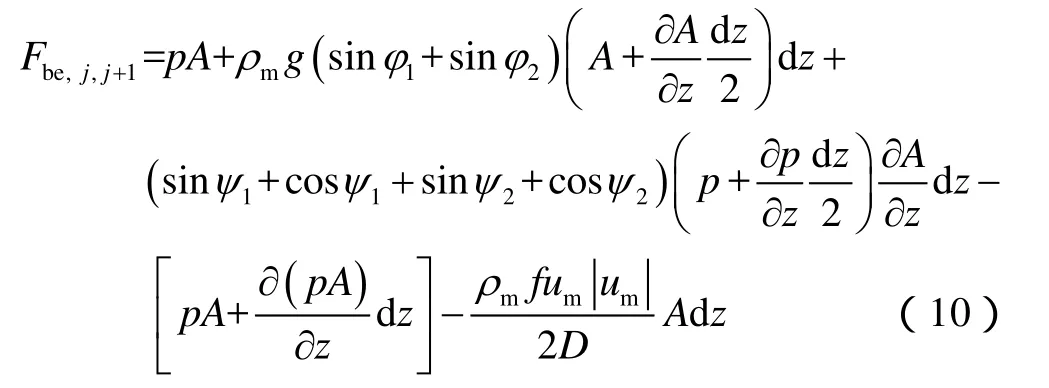
由此，可以得到满足气井瞬变流过程的运动方程形式，对直井段和造斜段分别列出牛顿第二定律方程。

故气井的瞬变流动过程可以分为 3个井段进行计算，如图5所示。

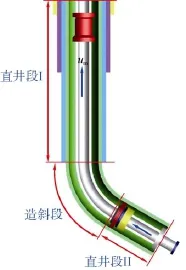
图5 气井水锤分段计算示意图

上述气井瞬变流模型在经典模型的基础上，考虑了竖直油管的重力因素、多相流影响以及造斜井段对流体的作用，该模型能更好地反映井下复杂环境，对油管内的流体瞬态运动情况做出精确的数学描述。

2 特征线法求解

对于瞬变流数学模型的求解，解析法与数值解法最为普遍。瞬变流模型是一对拟线性双曲偏微分方程，求出解析解存在很大的困难。数值解法对方程本身的要求较低，可以不对方程做较多简化，通过计算机模拟代替实际的模型实验，更有利于对工程问题进行研究。本文采用数值解法中常见的特征线法进行求解。

直井段与造斜段需要分开进行描述，此处以直井段Ⅰ（垂直）为例，建立并求解特征线方程组，造斜段与直井段Ⅱ（斜）的求解步骤与直井段Ⅰ类似。

2.1 特征线方程组

引入待定系数ω对直井段简化后的瞬变流基本微分方程进行线性化：

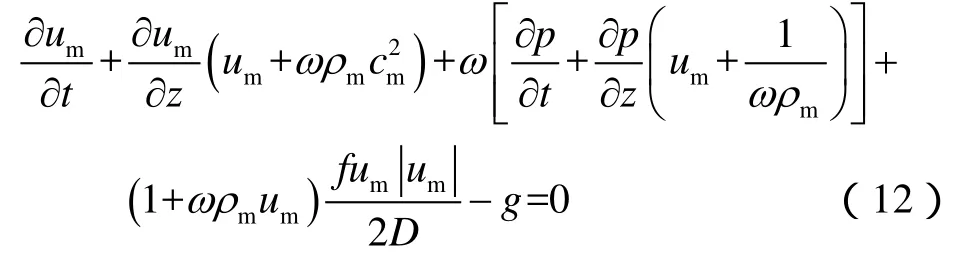
将线性化后的方程转化为常微分方程，并选取合适的ω，由此可以得到描述瞬变流过程的特征方程组。顺波特征线（C+）为：

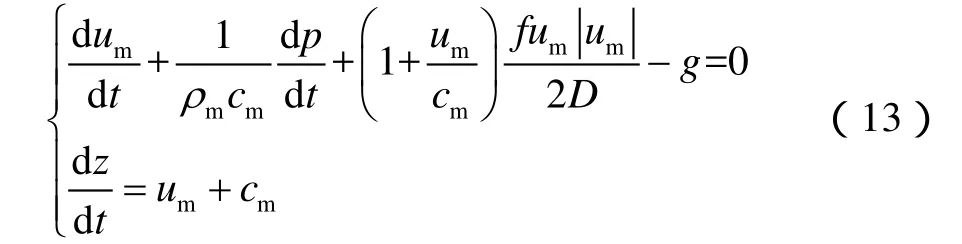
逆波特征线（C−）为：

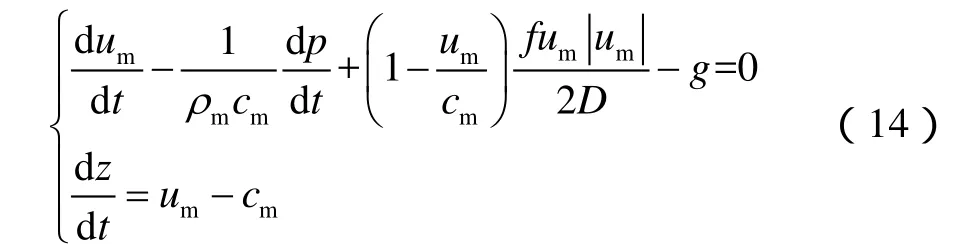
2.2 有限差分离散求解

通过有限差分法对井深和时间进行离散：将油管分为3段，分别是直井段Ⅰ、造斜段和直井段Ⅱ，油管微元长度为Δz；时间等分为M段，每段步长为Δt。以直井段Ⅰ为例，绘制特征网格L-t平面图，如图6所示。

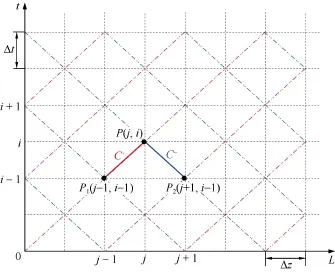
图6 特征网格L-t平面图

若已知点P1和P2所在井深分别为L1和L2，i时刻相应油管节点横截面的压力为pP1,i和pP2,i，流速为umP1,i和umP2,i，则点P在i+1时刻的压力和流速可由（13）和（14）式联立求得。重复此步骤，便可逐个求出后继时刻油管内所有节点的压力与流速，造斜段和直井段Ⅱ的求解步骤与之相同。

分别沿特征线C+和C−对（13）和（14）式进行差分，可得i时刻、任意节点j横截面的压力和流速：

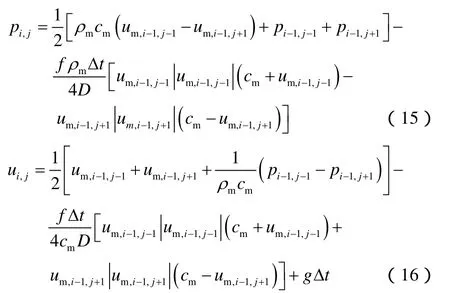
在气井波动压力和流速的求解过程中，油管每一节点的p和um初始值均为已知，先计算Δt时刻各节点的p和um，再计算下一时刻各节点的p和um，直到达到需要计算的时刻为止。

3 实例计算

3.1 计算分析

求解直井段与造斜段的联合离散方程计算量巨大，无法进行人工求解，需要通过计算机程序来实现气井瞬变流动的模拟计算。将实例井分为 3段计算，直井段Ⅰ离散为500段，造斜段离散为150段，直井段Ⅱ离散为 350段。定义井口阀门开度Kv满足如下函数：

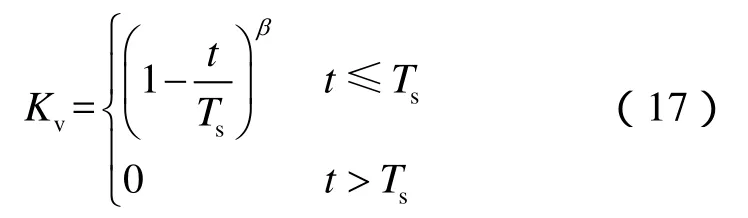
其中β为阀门开度系数，当β=1.0时为线性关阀。

将标准状况下的天然气产量转换为油管中的流量时，考虑到天然气的压缩性，需采用实际气体状态方程进行换算，其中天然气压缩因子Z是非常重要的参数。本文参照国家标准GB/T 17747[23]中的SGERG-88公式，使用高位发热量、相对密度和 CO2含量作为输入变量。在GB/T 17747中，用物性值计算天然气压缩因子的公式如下：

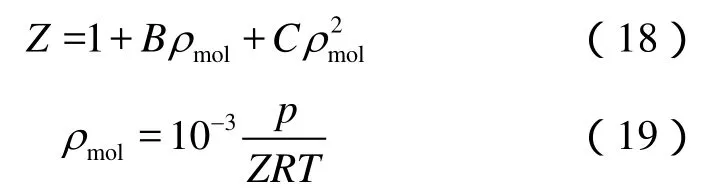
油管内不同微元体天然气压缩因子的值可由上式联立求得，（18）式中的B和C分别表示天然气的第二、第三维利系数，是高位发热量、相对密度、气体混合物中不可燃和可燃的非烃组分（CO2、H2）的含量及温度的函数，可根据GB/T 17747中的标准进行计算。

以XX6井为例模拟阀门关闭后井口的压力波动情况，分析不同的阀门开度系数、截面持液率和关阀时间对井口波动压力的影响。气井的基础数据见表1。

表1 XX6井物理及生产参数

3.2 结果分析

通过本文建立的多相流气井瞬变流动分析模型，计算得到XX6井井口的压力波动情况（见图7）。由图可见，阀门关闭瞬间，井口流体流速突变为0，压力迅速增大，在3.28 s时达到峰值32.65 MPa，之后以不同的梯度开始下降，在9.06 s时达到谷值26.48 MPa，然后开始压力波的下一次传播。因油管内的天然气易压缩，且在沿程摩擦阻力的作用下，波动压力会很快衰减，经过一段时间后，达到平衡压力。

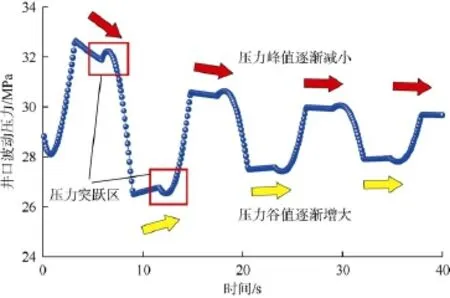
图7 XX6井井口波动压力模拟计算结果

阀门开度系数（β）是模拟瞬变流动过程一个重要的参数，它直接影响波动压力的峰值大小和幅值变化。取不同β值模拟计算瞬变流过程中的井口压力变化曲线（见图8a），并对图8a中红色矩形框部分进行局部放大（见图 8b）。由图8a可知，当β=1.5时，井口波动压力的峰值最大，可达33.07 MPa，且β值越大，井口波动压力的峰值越大。而图8b显示β值越大，井口波动压力变化幅度越平缓，压力传播过程中的压力突变区域越不明显；β值越小（以β=0.5为例），井口波动压力变化幅度越大，压力突变区越明显，突变区压力峰值最大达到32.79 MPa，数值大于最先到达井口的波动压力。虽然β值较大时会出现较大的波动压力，但较小的β值会造成油管内流体反复的压力扰动，从而引起油管的流固耦联振动，该问题是当下极难妥善解决的技术难题。所以应在不超过油管最大关井压力的基础上，尽量使用较大的阀门开度系数。

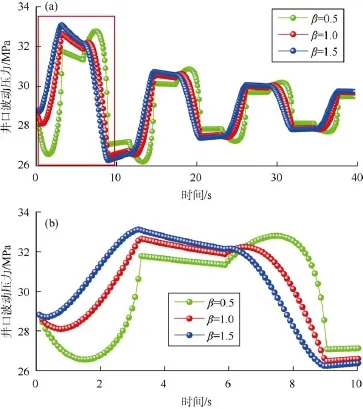
图8 不同阀门开度系数下井口波动压力模拟计算结果

截面持液率（HL）是研究多相流问题一个非常重要的参数，它是指在气液两相流动的过程中，液相的过流断面面积占总过流面积的比例。本文选取紧贴井口的一层流体为研究截面，对该截面不同HL值条件下的压力脉动进行计算（见图9a），并对图9a中红色矩形框部分进行局部放大（见图9b）。由计算结果可知，HL值越大，压力波的传播速度越大，传播周期越短。例如，随着HL值从0.03增加至0.10，压力拐点分别出现在 3.47，3.28，3.08，2.79 s，表现为依次缩短（见图9b中的红色矩形框）。

较大的HL值对应的波动压力变化幅度大，会引起油管内的压力扰动，同时较大的HL值对应的压力值也较大，且HL值的变化会引起较明显的波动压力变化。实际生产中可通过精确计算油管内流体的持液率，调整生产参数得到合适的HL值，控制波动压力的大小和变化幅度，减小水锤压力的冲击。

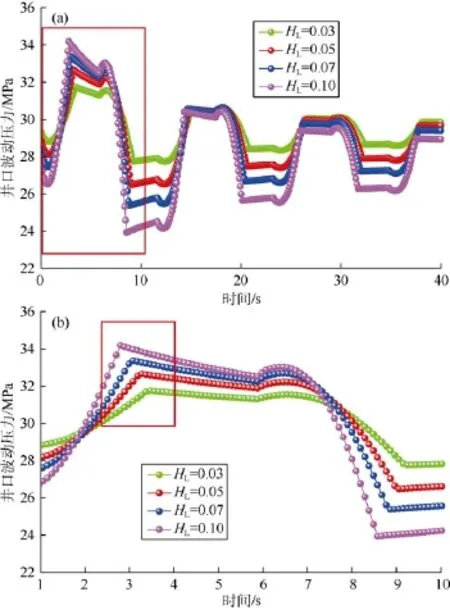
图9 不同截面持液率下井口压力模拟计算结果

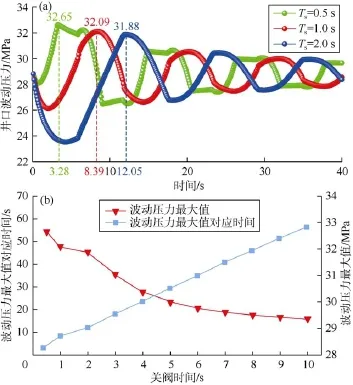
图10 不同关阀时间下井口波动压力模拟计算结果

不同关阀时间对井口波动压力峰值也有较大影响，图10a为3个不同关阀时间条件下井口波动压力的模拟结果，3条虚线的位置代表3个关阀时间对应的压力峰值。可以看到，关阀时间增加，井口最大压力值减小，峰值出现的时间也相应滞后。图10b为0.5～10.0 s关阀时间条件下，不同的井口波动压力峰值与其对应的时间。可以发现，短时间关井的压力波传播速度比较长时间关井的压力波传播速度要快。

XX6井是一口储气库井，井浅且高产，阀门瞬关会形成较大的压力波冲击，井口压力较大。随着关阀时间增加，水锤冲击压力减小，达到平衡压力的时间缩短。在深井或超深井中，沿程摩阻较大，天然气本身具有较强的压缩性，压力波衰减更快，此时压力波对井口的冲击较小。

通过气井瞬变流模型模拟气井瞬态关井，可以优化合理的阀门开度系数和关阀时间，减小水锤冲击对井口装置和油管造成的危害，保障井筒完整性。

4 结论

高产气井井口阀门关闭时开度系数越大，井口压力的峰值越大，波动压力的变化幅度越平缓，压力突变区越不明显。在保证不超过油管最大关井压力的前提下，使用较大的开度系数可减小压力波的冲击。

截面持液率越大，压力波速越大，传播周期越短；持液率越大，波动压力的变化幅度越大，压力越大。实际生产中，可通过调整生产参数得到合适的持液率，控制波动压力的大小和变化幅度，减小水锤的冲击。

采气树关阀时间增加，井口的最大波动压力值减小，峰值出现的时间也相应滞后，压力突变区逐渐消失；阀门关闭时间越短，压力波的传播速度越快。

气井瞬变流模型可以优化合理的阀门开度系数和关阀时间，减小水锤冲击对井口装置和油管造成的危害，保障井筒的完整性。

符号注释：

A，A1，A2——油管横截面面积，m2；B——天然气第二维利系数，m3/kmol；C——天然气第三维利系数，m6/kmol2；C+——顺波特征线；C−——逆波特征线；cm——压力波速，m/s；D——油管外径，m；e——油管壁厚，m；Eg——气体弹性模量，Pa；EL——液体弹性模量，Pa；Ep——管壁弹性模量，Pa；f——范宁摩阻系数，无因次；Fbe——造斜段油管所受合外力，Pa；Fc——造斜段油管弹性膨胀力，Pa；Fs——油管膨胀造成的平均侧向力，Pa；Fve——直井段油管所受合外力，Pa；g——重力加速度，m/s2；G——油管重力，N；hw,1,2——水头位置 1到 2的沿程摩阻，m；HL——截面持液率，%；i——时间节点编号；j——空间节点编号；Kv——阀门开度，无因次；L——气井井深，m；M——时间段数，段；p——油管内压力，Pa；p0——井口压力，Pa；p1，p2——水头位置 1，2处的压力，Pa；pP1,i，pP2,i——i时刻点P1和P2处油管节点横截面的压力，Pa；P，P1，P2——特征网格L-t平面图上的点；pin——微元体入口流压，Pa；pout——微元体出口流压，Pa；R——通用气体常数，J/（mol·K）；t——时间，s；T——天然气温度，K；Ts——关阀时间，s；u0——井口流速，m/s；um——气液混合相流速，m/s；um,0——气液混合相初始流速，m/s；um,1，um,2——水头位置1、2处气液混合相流速，m/s；umP1,i，umP2,i——i时刻点P1和P2处油管节点横截面的流速，m/s；z，z1，z2——水头位置，m；Z——天然气压缩因子，无因次；α1，α2——水头位置1，2的动能修正系数，无因次；β——阀门开度系数，无因次；Δp——油管内的压力增量，Pa；Δt——时间步长，s；Δz——井深步长，m；ρm——气液混合相密度，kg/m3；ρmol——摩尔密度，kmol/m3；τ——油管壁面剪切应力，Pa；φ，φ1，φ2——油管轴线与水平位置的夹角，（°）；Ψ，Ψ1，Ψ2——油管侧壁与轴线的夹角，（°）；ω——拟合待定系数，m2·s/kg。