基于卷积神经网络的径向复合油藏自动试井解释方法

李道伦，刘旭亮，查文舒，杨景海，卢德唐

（1.合肥工业大学，合肥 230009；2.大庆油田测井技术服务分公司，黑龙江大庆 163453；3.中国科学技术大学，合肥 230026）

0 引言

人工智能方法因其处理高度复杂问题的突出能力，引起了石油行业研究者的特别关注[1-4]。传统人工神经网络已在石油工程领域得到广泛应用。李道伦等[5]利用神经网络的隐式方法来预测未知年份的测井数据，进而提出基于隐式曲线与神经网络的时间序列处理新方法[6]。Asadisaghandi等[7]利用神经网络预测油品压力-体积-温度属性。Enab等[8]利用正向和反向神经网络来预测产气剖面等。Singh等[9]利用人工神经网络估算孔隙度。Memon等[10]采用径向基神经网络构建动态井代理储集层模型预测井底流动压力。Kim等[11]利用神经网络选择页岩气储集层完井方法。最近，Choubineh等[12]利用神经网络模型来估算气-原油的最小混相压力。

20世纪90年代以来，传统人工神经网络在试井解释中得到了应用。Athichanagorn等[13]使用神经网络来识别导数图的特征。邓远忠等[14]将导数曲线的峰值及径向流水平线位置作为 3层前馈神经网络的输入，来预估试井参数。Jeirani等[15]将霍纳图输入神经网络来估计油藏压力、渗透率和表皮系数。Adibifard等[16]将压力导数数据的插值切比雪夫多项式的系数作为神经网络的输入来估计储集层参数。Ghaffarian等[17]将拟压力导数数据作为单一和耦合多层感知器网络的输入，识别凝析气藏模型。然而，基于传统人工神经网络的试井解释方法存在以下问题。首先，将压力导数曲线的部分特征作为神经网络的输入，导致试井自动解释困难，例如，仅将切比雪夫多项式系数作为网络输入[16]。其次，试井曲线复杂多变，需要大量数据来训练网络。然而，传统的3层或4层网络往往会训练失败，这限制了其自动解释的能力。

深度学习是机器学习的一个新领域。深度学习的本质是构建含有多个隐藏层的网络模型，通过学习大规模的数据，获得更具代表性的特征，从而提高预测和分类的精度。近年来，深度学习也开始被应用于石油领域。Tian等[18]利用递归神经网络学习永久井下压力计（PDG）数据，用于识别油藏模型及生产预测。Sudakov等[19]将深度学习用于渗透率预测。ZHA等[20]利用深度学习进行三维多孔介质重构。张东晓等[21]利用循环神经网络研究测井曲线的生成与修补。卷积神经网络是深度学习算法的一个重要组成部分，它和传统神经网络的区别在于：①卷积神经网络打破了传统神经网络对层数的限制，可增加网络层数，成为深度网络；②卷积神经网络采用特征学习的方法，通过逐层提取特征的方式使得预测或分类问题更易实现。卷积神经网络研究始于20世纪80年代，时间延迟网络和LeNet-5网络是最早的卷积神经网络[22-23]。进入21世纪后，随着深度学习理论的引入、数据的增加以及计算设备的改进，卷积神经网络迅速发展。Krizhevsky等[24]提出的 AlexNet网络得到广泛应用，之后卷积神经网络也在石油领域得到应用[25]。

本文提出一种基于卷积神经网络的径向复合油藏自动试井解释方法，将压力变化及其导数数据输入到网络中就可解释出地层参数，无需人工调参拟合，实现解释自动化。利用大庆油田现场实测数据验证本文方法的有效性和准确性。

1 方法概述

1.1 径向复合油藏模型及试井解释参数

径向复合油藏模型由两个参数属性不同的区域组成，即以井为中心的圆形内区和无限大外区。径向复合油藏模型可以描述井周围的污染或改善、远井区的径向岩性或流体性质的变化。径向复合油藏模型的基本假设为：①地层水平，等厚，均质，各向同性；②内、外区流体均为单相微压缩流体，流动符合达西定律；③开井前地层各处压力相等；④考虑井储效应和井筒污染，忽略重力。

本文使用的试井曲线为Gringarten-Bourdet复合曲线，其由Gringarten压力曲线和Bourdet压力导数曲线组成[26-27]。考虑到方法普适性，本文方法使用无因次参数。因此，径向复合油藏模型试井解释参数为：流度比M、储容比F、无因次复合半径RfD及无因次组CDe2S，取对数形式，即 lg(M)，lg(F)，lg(RfD)及 lg(CDe2S)。无因次组可表征井储和表皮效应。无因次复合半径的定义为：

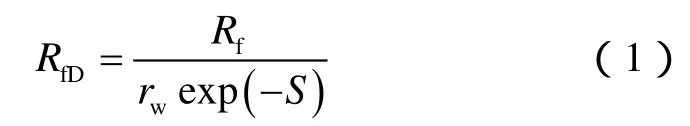
（2）式和（3）式分别定义了内、外区的流度比和储容比：

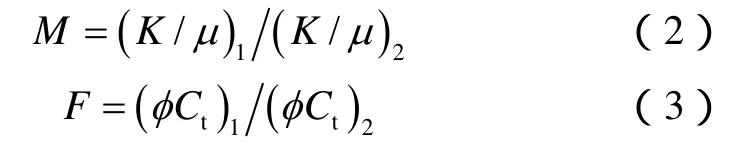
1.2 卷积神经网络

卷积神经网络是一种深度前馈神经网络。卷积神经网络主要由输入层、卷积层、池化层、全连接层和输出层构成。卷积层通常有若干个，池化层位于卷积层之后，全连接层通常在网络末端。激活函数跟随在卷积层和全连接层之后，为网络增加非线性。卷积层中输入与卷积核之间会进行卷积运算。卷积运算通常用*号表示，设f(x)，g(x)为实数域上的两个可积函数，则它们的卷积结果为：

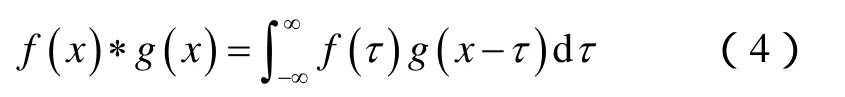
数列x(n)和h(n)的卷积结果为：

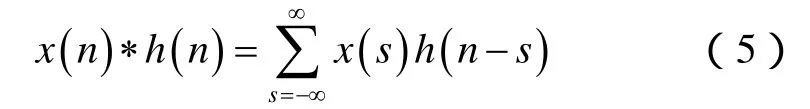
卷积层的输入和卷积核通常是多维数组数据，卷积运算可以被看作是卷积核在输入数据上滑动的过程：将卷积核的各个元素与其在输入数据上覆盖的对应位置的元素相乘再求和得到未激活的神经元，最后滑动完所有的输入数据。例如，给定一个二维输入xij和二维卷积核fuv，其中 1≤i≤N1，1≤j≤N2，1≤u≤n1，1≤v≤n2。通常情况下，n1≤N1，n2≤N2。这时卷积结果为：

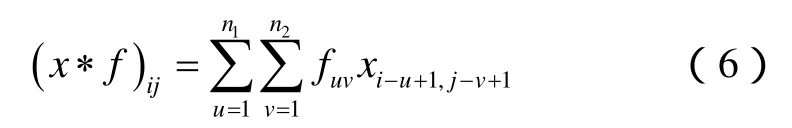
图1展示了一个二维数组卷积的例子[28]。

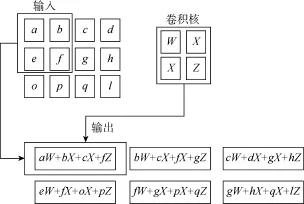
图1 二维数组卷积示例

与传统神经网络不同的是，卷积操作通过两个重要特性提高网络性能：局部连接和权重共享。传统人工神经网络通常使用矩阵乘法来构建输入和输出之间的连接，这种形式的连接是完全连接，意味着每个输出神经元都与每个输入神经元相互连接。然而，卷积神经网络具有局部连接的特点，即每个输出都连接一部分输入，这大大减少了参数的数量，使网络易于训练。局部连接使神经元只对局部进行感知，在更高层将低层局部的信息综合起来得到全局信息，这大大增强网络特征提取能力。在全连接中每个连接具有不同的权重。然而，卷积层中，一组连接可以共享相同的网络权重，而不是每个连接的权重都不同。局部连接和权重共享使卷积神经网络在统计效率和存储需求上都大大优于传统人工神经网络。本文网络的输入为100×100矩阵且有18层卷积层，从输入到第18层卷积层一共有590 688个参数。若采用全连接方式且每个隐藏层有200个神经元，则从输入到第18层隐藏层会产生2.621 44×1045个参数，远远多于采用卷积操作的参数数量。

池化也叫下采样，它提取出某一位置相邻区域的总体特征作为该位置的输出。池化方法在保留信息的同时减少了数据量，大大降低了特征维数和网络参数数量。常见的池化方法有最大池化和平均池化。最大池化取相邻区域内特征点的最大值，平均池化取相邻区域内特征点的平均值，图2展示了最大池化的示例。本文网络的输入为 100×100矩阵，经过第一层池化层后变为 50×50的矩阵，大大降低了特征维数，使网络更易训练。

图2 最大池化示例（在2×2的矩形区域内选择最大值）

可见，与传统人工神经网络相比，卷积神经网络参数更少，更容易训练，提取特征更有效，学习能力和性能显著提高。

1.3 基于卷积神经网络的自动试井解释方法

基于卷积神经网络的自动试井解释方法的具体步骤如下。

①数据收集与预处理。人工智能本身就是一种数据科学，卷积神经网络也不例外。本文一共取得径向复合油藏 2×105组双对数图及其对应的油藏参数组合lg(M)，lg(F)，lg(RfD)及 lg(CDe2S)，其中 199 820组是由解析法生成的模拟数据，其余为现场实测数据。生成模拟数据时，参数的取值范围如表1所示。

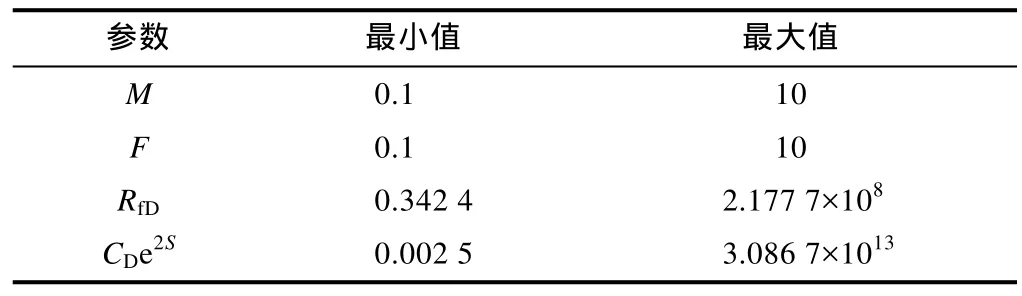
表1 生成模拟数据时的参数取值范围

每个模拟双对数图中的压力及导数曲线各有 200个数据点，而现场实际图往往不完整，每个曲线各有100～110个数据点。为了保持输入维度的一致性，在每次迭代训练时，选取100个连续点。

在实际应用中，卷积神经网络通常用于目标识别，其输入是图像的像素值，这是 1个二维或三维矩阵。因此，在训练前，需要将上一步生成的数据转换为矩阵：对于每个双对数图，分别复制选取的 100个压力数据点和 100个压力导数数据点再连接在一起形成 1个100×100的矩阵。

②卷积神经网络的训练和优化。将经过步骤①转换后的矩阵和对应的参数组合lg(M)，lg(F)，lg(RfD)及lg(CDe2S)分别作为卷积神经网络的输入和输出，90%、5%和 5%的数据分别用于训练、验证和测试。损失函数为均方误差。均方误差的计算式为：

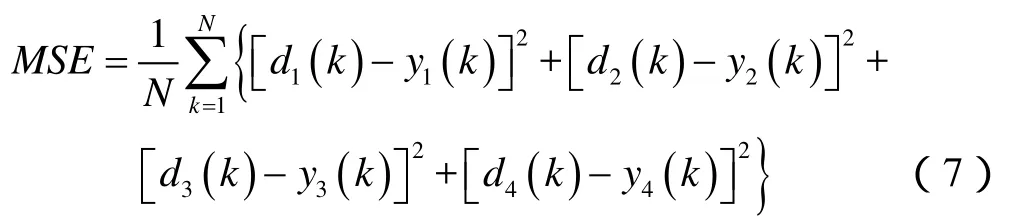
训练数据的均方误差越小，网络的拟合效果越好。在反复实验中对网络进行优化，优化过程包括改变网络深度、宽度、超参数等，加入正则化方法或其他优化方法，最终得到最优的网络配置。本文得出的最优卷积神经网络包含18个卷积层，3个池化层和3个全连接层。每个卷积层和全连接层的输出均经过 ReLU（线性整流函数）激活。ReLU函数的输出值为自变量与零之间的最大值，其使部分神经元输出为零，增加了网络的稀疏性，减少了训练时间。网络采用了“dropout”方法[24]，其在正向传播中将每个隐藏神经元的输出以一定的概率设为零，可以避免出现过拟合。初始学习率为0.000 1，为了使模型在训练后期更加稳定，本研究采用指数衰减的方法在每次迭代训练时逐步降低学习率。

③利用训练好的最优网络进行试井参数解释的自动初拟合。将测得的压力数据转换成双对数图，再重新排列成矩阵，输入训练好的最优卷积神经网络中，输出为 lg(M)，lg(F)，lg(RfD)及 lg(CDe2S)，从而得到M，F，RfD及CDe2S，实现了试井参数解释的自动初拟合。

④移动曲线，解释出井筒和地层参数。将M，F，RfD及CDe2S输入到商业软件中可得到典型曲线图，移动典型曲线图，使之与实测双对数图重合，从实测曲线上任取一点，记下该点的压力变化值Δp和时间值t，同时也查出该点在典型曲线上的无因次压力变化值pD和无因次时间值tD。利用该点的 Δp，t，pD和tD以及参数M，F，RfD及CDe2S的值，就可以根据一系列公式计算出井筒存储系数、表皮系数和内、外区渗透率等井筒和储集层参数[29]。

2 结果与讨论

2.1 本文方法与基于人工神经网络的方法的差异

本文方法直接将整个压力变化及其导数数据作为网络的输入，而在以往基于人工神经网络的方法中，输入是从压力变化及其导数数据中获得的特征。例如，邓远忠等[14]使用导数图的峰值和径向流的水平位置作为神经网络的输入，Adibifard等[16]使用插值切比雪夫多项式的系数作为神经网络的输入。

2.2 卷积神经网络性能验证

验证集和测试集数据用于验证训练后的最优卷积神经网络的解释精度。表 2给出了验证集和测试集数据解释值的平均绝对误差，可以看出 4个油藏参数的平均绝对误差都很小，说明网络训练得很好，具有很好的泛化能力。

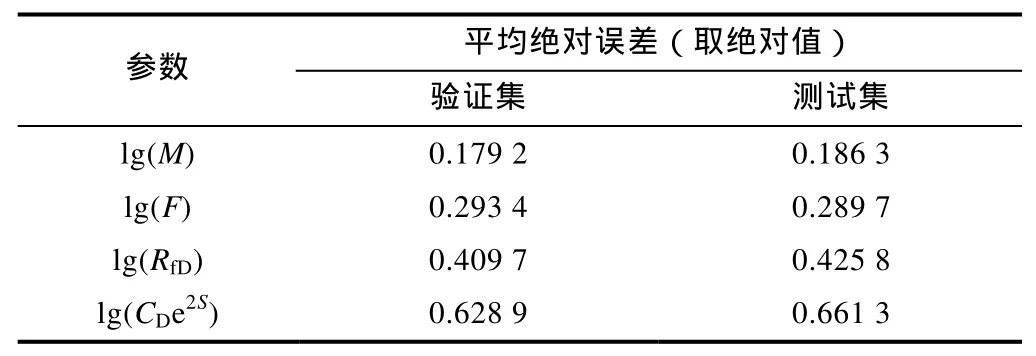
表2 验证集和测试集数据解释值的平均绝对误差

为了更清楚地展示本文方法的解释效果，分别从验证集和测试集中抽取了 3个样本，用来进一步展示训练后的卷积神经网络的性能。样本Val1，Val2，Val3取自验证集，样本 Test1，Test2，Test3取自测试集。解释结果如表3所示。

表3 选取的6个样本的参数解释值及其绝对误差

从表3可以看出，对于 6个样本，本文提出的卷积神经网络解释的参数与真实参数的误差整体上较小。然而样本 Val2的 lg(F)，样本 Val3的 lg(M)及lg(CDe2S)，样本 Test2的 lg(M)，lg(F)和 lg(CDe2S)的解释值的误差较大，其中 lg(M)和 lg(F)解释值误差大主要是由数据截取误差引起，当没能截取全部特征时，解释效果不好。下面以样本Test2为例详细解释原因。样本Test2的原始曲线和截取的曲线如图3所示。可见，测试时截取的曲线没有包含原始曲线后期上翘的部分，而这一部分正是表征流度比和储容比的关键，这是导致该样本流度比和储容比解释效果差的原因。样本Test2的参数lg(CDe2S)绝对误差相对较大，但其相对误差为0.167 5，较小。图4表明，分别由解释值与真实值得到的两条双对数图的前期曲线基本重合，而曲线前期峰值及其前后是表征 lg(CDe2S)的关键。这说明解释误差较小。

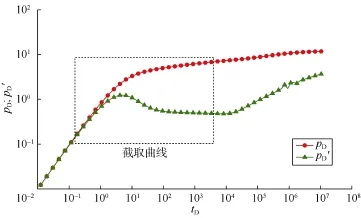
图3 样本Test2的原始曲线和截取曲线

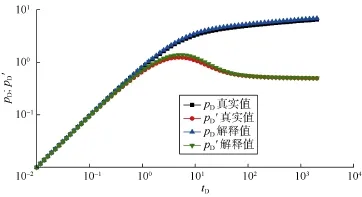
图4 样本Test2的解释值与真实值对比（只截图了前半部分）

2.3 现场实例分析

利用大庆油田的6个现场实例资料，进一步验证本文方法的有效性。表4给出了6个现场实例的基本参数。

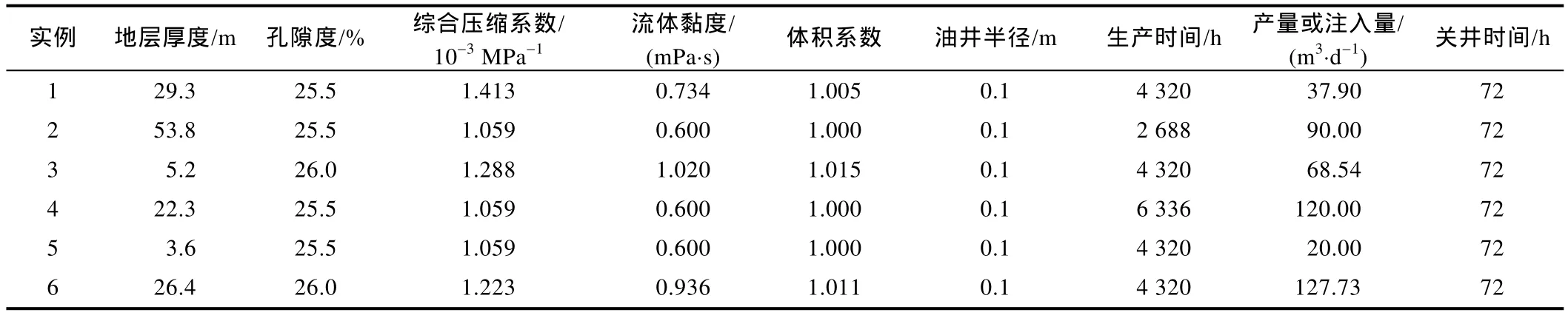
表4 6个现场实例的基本参数

图5—图10给出了本文方法与解析法的计算结果对比，表 5给出了相应的解释参数。由图 5a和图 6a可知，对于无噪音或有轻微噪音的实测数据，本文方法能正确解释出地层参数，这从实测曲线与计算曲线几乎重合可以看出。随着噪音的增加，解释结果仍然很好，如图 7a和图 8a所示。甚至当实测数据有杂乱噪音时，训练好的卷积神经网络仍然能近乎完美解释出地层与井筒参数，如图9a所示。即使当实测数据在局部上下振荡时，图 10a表明解释结果仍然很好。这证明了本文方法的有效性和鲁棒性。即使训练样本中存在部分“坏样本”，训练后的卷积神经网络仍能正确解释实测关井压力数据。这说明，少量的“坏样本”不会影响卷积神经网络的性能，只是不能正确解释出“坏样本”所对应的参数。若剔除“坏样本”，可以预见训练后的卷积神经网络将有更优异的表现。如何剔除“坏样本”将是今后的研究内容之一。

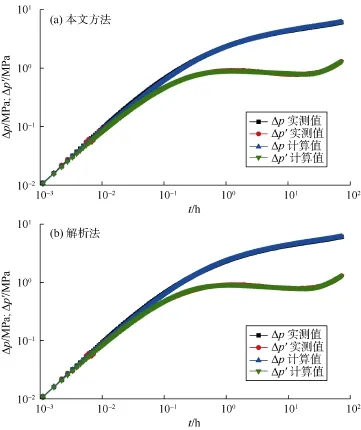
图5 实例1本文方法与解析法计算结果对比

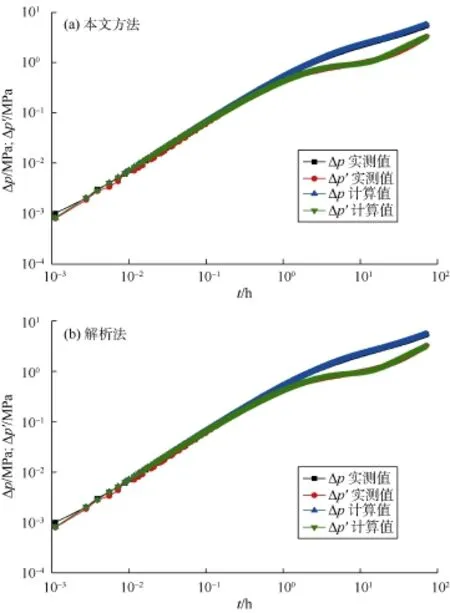
图6 实例2本文方法与解析法计算结果对比

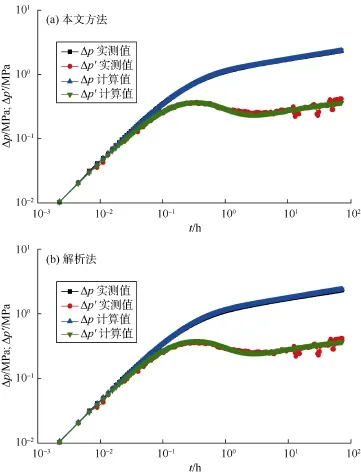
图7 实例3本文方法与解析法计算结果对比

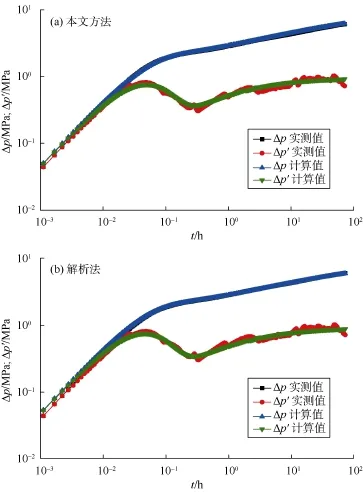
图8 实例4本文方法与解析法计算结果对比

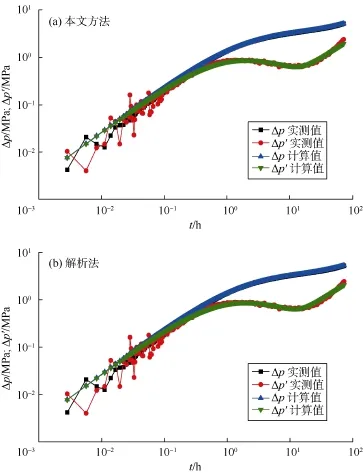
图9 实例5本文方法与解析法计算结果对比

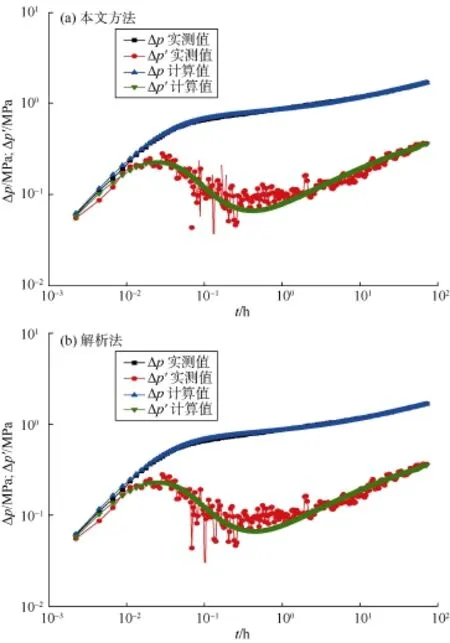
图10 实例6本文方法与解析法计算结果对比

此外，通过与解析法对比发现，本文方法解释结果与解析法解释结果差距较小，两种方法都可以得到很好的解释结果。但是，解析法需要专业的试井人员操作完成，耗费大量的人力和时间。而本文方法可自动解释，只需将实测数据转化为矩阵输入到训练好的卷积神经网络中，输出即为所需解释的参数，即使是不具备专业知识的人员也可操作，这大大提高了工作效率。

可以看出，本文提出的基于卷积神经网络的试井解释新方法能够高精度地自动解释出径向复合油藏参数，显著提高工作效率，实现试井解释的自动化。

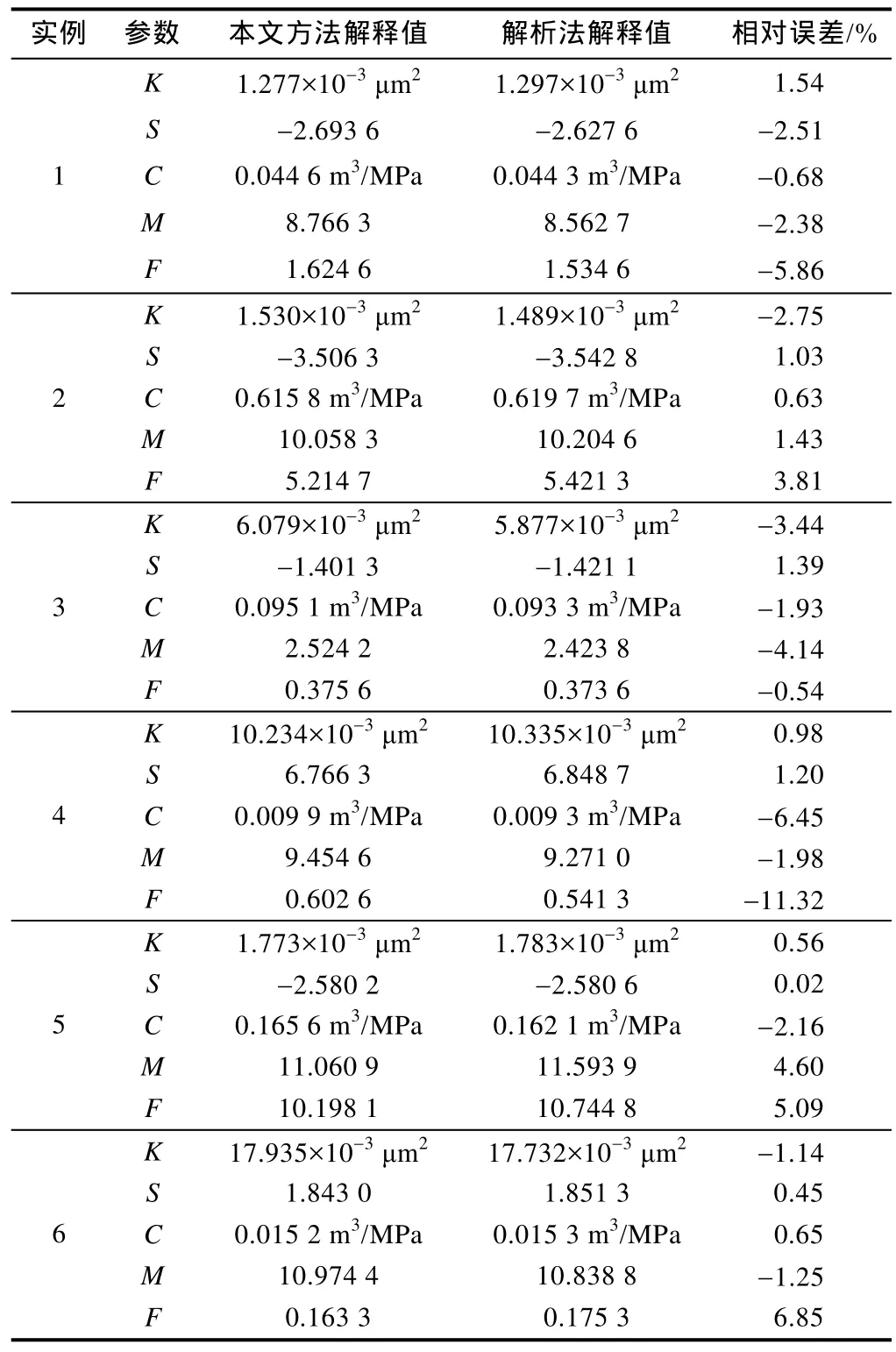
表5 本文方法与解析法的解释参数对比

2.4 本文方法与最小二乘法的对比

选取两个最有代表性的实例（实例1与实例6）将本文方法与最小二乘法进行对比，实例1的噪音很小，而实例6有较为杂乱的噪音。从图11、图12及表6中可以看出，由最小二乘法得出的结果较差，且最小二乘法涉及选取拟合参数问题，无法真正做到自动化的试井解释。

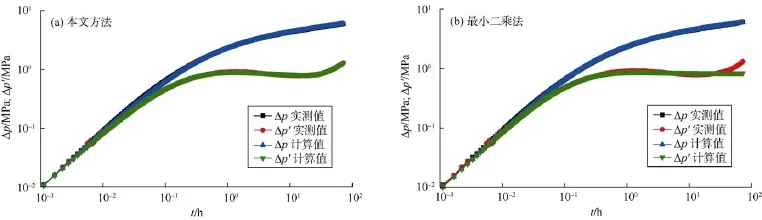
图11 实例1本文方法与最小二乘法计算结果对比

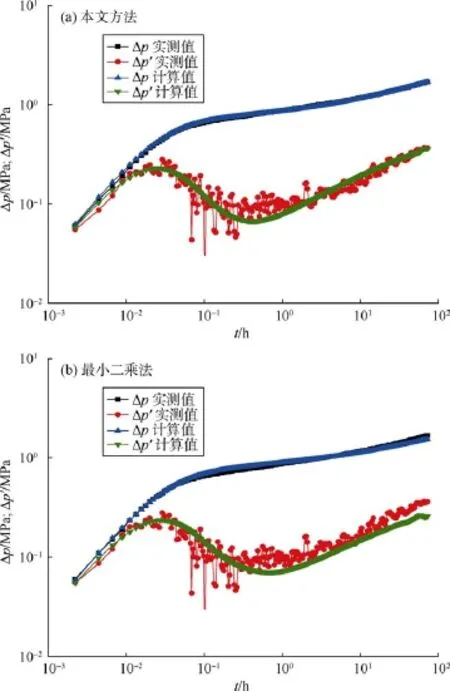
图12 实例6本文方法与最小二乘法计算结果对比

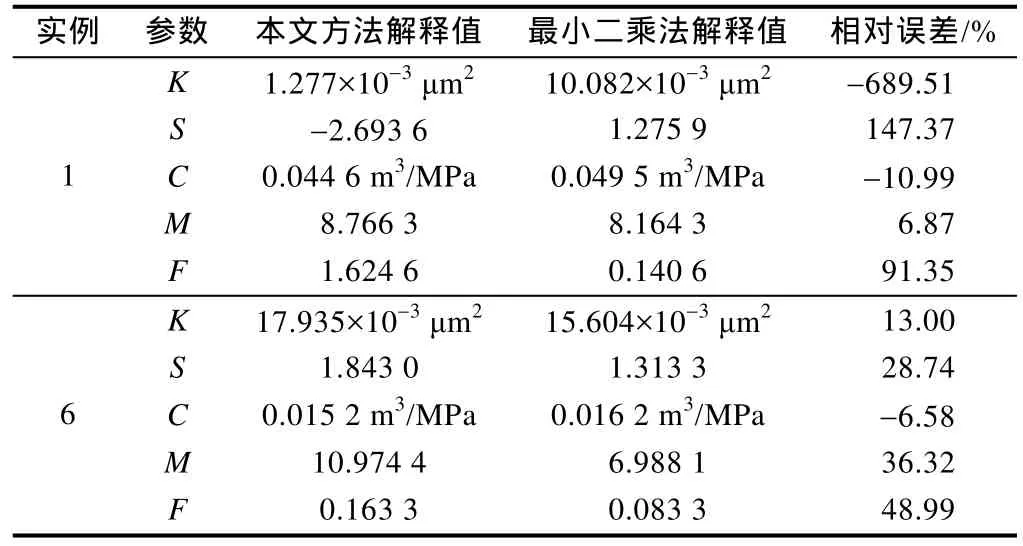
表6 本文方法与最小二乘法的解释参数对比

3 结论

提出了基于卷积神经网络的径向复合油藏自动试井解释方法。将压力变化及其导数数据作为输入，对应的参数组合作为输出，训练后的卷积神经网络就可自动解释压力数据，给出径向复合油藏参数。该方法实现了试井参数解释的自动初拟合，可大幅提高试井解释效率。利用大庆油田的实测数据验证了本文方法的有效性和鲁棒性，且发现本文方法优于解析法和最小二乘法。

本文方法不能简单照搬到其他类型油藏。不同类型油藏的试井曲线特征、参数个数等都有很大差异，导致神经网络架构及相关处理方法不同。

符号注释：

B——体积系数，m3/m3；C——井筒存储系数，m3/MPa；CD——无因次井筒存储系数；Ct——综合压缩系数，Pa-1；d1(k)，d2(k)，d3(k)，d4(k)——第k个参数组合中 lg(M)，lg(F)，lg(RfD)及 lg(CDe2S)的解释值；fuv——二维卷积核；f(x)，g(x)——函数；F——储容比，无因次；h(n)，x(n)——数列；H——地层厚度，m；i，j——二维输入的行、列序号；K——渗透率，10-3μm2；M——流度比，无因次；MSE——均方误差；n，s——数列长度；n1，n2——二维卷积核的行数、列数；N——参数组合数目；N1，N2——二维输入的行数、列数；pD——无因次压力变化，pD=2πKHΔp/QBμ；pD′——无因次压力变化导数，pD′=tDdpD/dtD；Δp——压力变化，MPa；Δp′——压力变化导数，Δp′=ΔtdΔp/dΔt，MPa；Q——产量，m3/s；rw——井筒半径，m；Rf——复合半径，m；RfD——无因次复合半径；S——表皮系数，无因次；t——时间，h；Δt——时间变化，h；tD——无因次时间，tD=Kt/φμCtrw2；u，v——二维卷积核的行、列序号；x，τ——函数自变量；xij——二维输入；y1(k)，y2(k)，y3(k)，y4(k)——第k个参数组合中lg(M)，lg(F)，lg(RfD)及 lg(CDe2S)的真实值；μ——流体黏度，mPa·s；φ——封堵层孔隙度，%。下标：1——内区；2——外区。