核心素养下中考数学测评研究——以2019年武汉市中考数学试题为例

朱思奥，太会娟，潘继斌

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

核心素养是知识与技能、过程与方法、情感态度与价值观的综合表现。2014年3月，教育部《关于全面深化课程改革，落实立德树人根本任务的意见》中指出，研究制定学生发展核心素养体系和学业质量标准，要根据核心素养体系，明确学生完成不同学段、不同年级、不同学科学习内容后应该达到的程度要求。以数学核心素养为视角研究作为终结性评价的中考数学试题，有助于初中数学教师对数学核心素养的理解，帮助学生成长和形成终身发展的必备品格和关键能力。

1 对试卷整体分析与数学核心素养的考查

1.1 试卷整体分析

整体上来看，2019年武汉市中考数学试题，是一套高水准的毕业考试试卷。在对基础知识、基本图形、基本方法及基本能力考查的同时，也着眼于考查学生的数学核心素养。在命题思路上，遵循《课程标准》的要求，试题源于课本，并适当拓展加深，编排具有起点低、坡度缓、难点分散等特点。

2019年武汉市中考数学试卷满分120分，时间为120分钟，全卷包括Ⅰ卷和Ⅱ卷。Ⅰ卷为选择题，Ⅱ卷为非选择题。试卷包括选择题、填空题和解答题三种题型。选择题12小题，每题3分，共36分；填空题4小题，每题3分，共12分；解答题9题，共72分。数与代数、图形与几何、统计与概率、综合与实践4个部分在试题中所占的比重与它们在教学中所占课时的百分比大致相同，数与代数约占45%，图形与几何约占40%，统计与概率约占15%，综合与实践的考查渗透在上述3个部分中。

试卷最大的变化在于容易题、中档题、难题比例的变化，由去年的7∶2∶1变成6∶3∶1，整套试题难度系数在0.65左右。整套试题计算量较大，对学生的数学运算能力要求较高。整体上来说，试卷较为新颖，对于学生的灵活处理问题要求较高，因此基础知识扎实且做题比较灵活的学生会取得较好的成绩。

1.2 数学核心素养的考查

核心素养是三维目标的发展与超越。在测试题中它们交叉呈现、各有侧重，且与四基融合在一起。表1列出了典型试题所涉及的知识领域、四基指向以及核心素养。

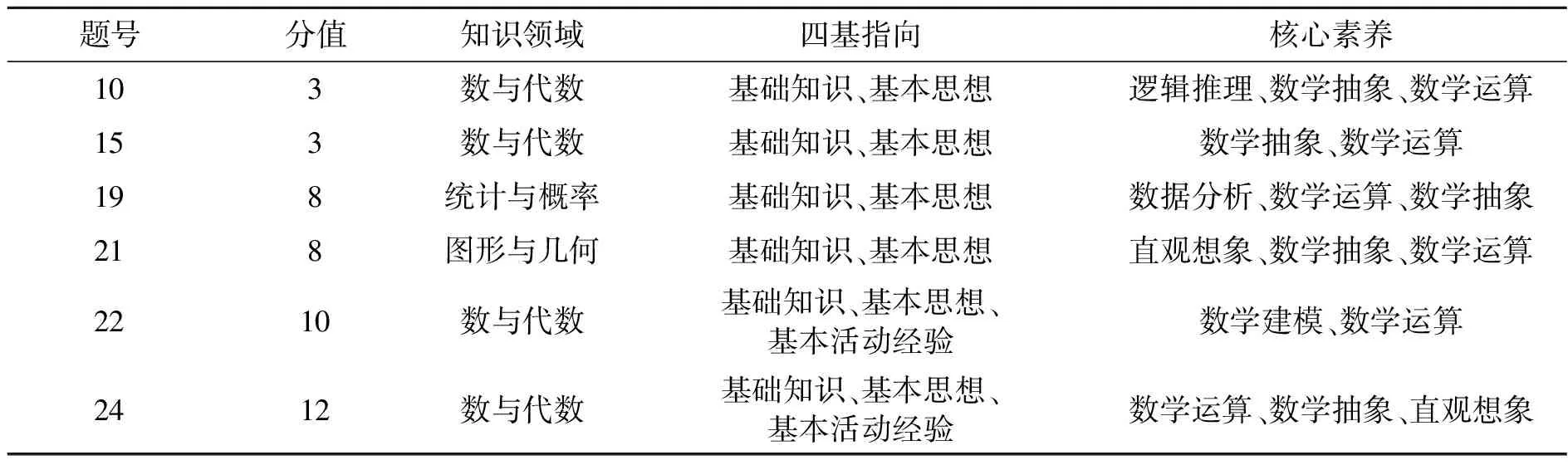
表1 典型试题涉及的知识领域、四基指向以及核心素养

2 典型试题对数学核心素养考查分析

湖北省中考一直都是各地级市统一命题，2019年武汉市共有6.98万名初中毕业生参加了中考，平均分77.20分，及格率56%，优秀率7%，及格率偏低，优秀率与往年持平。事实上，学生在触及到考查数学核心素养的题目上得分不理想。下面选择其中的典型试题为例进行数学核心素养考查分析。

2.1 数学抽象素养的考查

数学核心素养考查分析：

数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养。题目以抛物线为背景，考查一元二次方程、平移的性质等知识，难度一般，主要是要找到解本题的切入点。此题以考查数学抽象为主，同时考查直观想象的数学素养。

学生解题分析：

此题是需要观察a(x-1)2+c=b-bx通过y=ax2+bx+c向右平移一个单位得来的，从而算出解为(-2,0)与(5,0)。这道题有近五成的学生并没有作答，也有部分学生解题思路出现错误：将A与B两点坐标带入y=ax2+bx+c中，计算不出a,b,c的值。由此可以看出，此类学生数学功底较弱，且数学抽象素养有待提升。

2.2 数学建模素养的考查

例：22.某商店销售一种商品，经市场调查发现，该商品的周销售量y(件)是售价x(元/件)的一次函数。其售价、周销售量、周销售利润w(元)的三组对应值如表2：

表2 商品销售表

注：周销售利润=周销售量×(售价-进价)

1)①求y关于x的函数解析式(不要求写出自变量的取值范围)；

2)由于某种原因，该商品进价提高了m元/件(m>0)，物价部门规定该商品售价不得超过65元/件，该商品在今后销售中，周销售量与售价仍然满足1)中的函数关系。若周销售最大利润是1400元，求m的值。

数学核心素养考查分析：

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养。本题考查一次函数、二次函数的应用，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型。

学生解题分析：

数学建模意识较弱的学生在第1问求函数关系式时，没有理解题意出现错误。例如，少部分学生列出y的函数关系式为y=售价-进价=x-40.在第3问上，一些学生只是将函数表达式列了出来，但并没有求出m的值，或是分析题目思路出现错误，说明此类学生二次函数的基本功还是不够扎实。

数学运算素养薄弱的学生会出现这两种错误：

2.在第3问上，有同学在配方上出现错误，如：

2.3 数据分析素养的考查

例：19.为弘扬中华传统文化，某校开展“汉剧进课堂”的活动。该校随机抽取部分学生，四个类别：A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”，调查他们对汉剧的喜爱情况，将结果绘制成如下两幅不完整的统计图，根据图中提供的信息，解决下列问题。如图1所示。

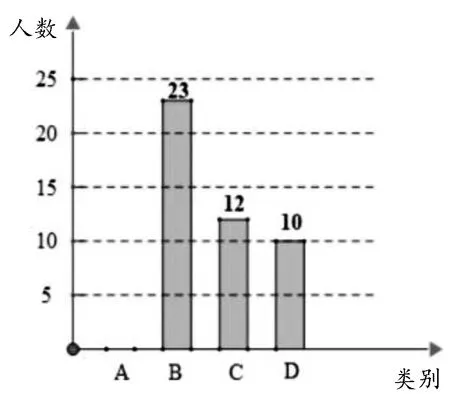
图1 武汉市2019年中考数学第19题图

2)将条形统计图补充完整；

3)该校共有1500名学生，估计该校表示“喜欢”的B类的大学生大约有多少人？

数学核心素养考查分析：

数据分析是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养。本题考查了频数分布直方图、扇形统计图等知识。熟悉样本，以及用样本估计总体是解题的关键，另外需要注意学会分析图表计算扇形的圆心角度数。

学生解题分析：

本题是七年级下册第十章第1节问题1的改编，学生的错误主要在于对统计知识和数据处理不够熟练。

在第1问上，有近3成的学生已经求出了总共人数是50人，但不知如何求出D类圆心角的大小；也有少部分学生出现低级错误，用720×20%或180×20%计算D类所对应扇形圆心角大小。

在第3问上，部分学生将简单问题复杂化，在之前第1问和第2问中算出了A，D所占百分比，于是通过1500×(1-20%-10%-24%)=1500×56%.

个别学生对第3问题目理解不清，写出这种错误答案：B类学生在680～710人数之间。

2.4 直观想象素养的考查

例：21.已知AB是圆O的直径，AM和BM是圆O的两条切线，DC与圆O相切于点E，分别交AM，BN于D、C两点。

1)如图2(a)，求证AB2=4AD×BC；

2)如图2(b)，连接OE并延长交AM于点F，连接CF，若∠ADE=2∠OFC，AD=1,求图中阴影部分的面积。

(a)

(b)

数学核心素养考查分析：

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养。此题考查了勾股定理、三角形的垂直平分线以及等腰三角形和扇形面积公式。在第1问中，作出辅助线是解本题的关键，需构造一个矩形，再利用勾股定理即可证明AB2=4AD×BC，第2问的难点是要求出∠BOE的度数。

学生解题分析：

直观想象较强的学生直接将辅助线作出并证明AB2=4AD×BC，而直观想象素养较弱的学生知道将OD，OC,OE连接，但并没有推理出ΔODE与ΔCOE相似。同样在第2问中，一些学生并没有推理出△COF为等腰三角形，或是在求阴影部分的面积时，有学生利用2个△OBC的面积减去扇形OBE的面积，但在计算过程中，并没有算出扇形OBE的面积。可见这类学生在直观想象以及逻辑推理素养上有待加强。

2.5 数学运算素养的考查

例：24.已知抛物线C1：y=(x-1)2-4和C2：y=x2.

1)如何将抛物线C1平移得到抛物线C2？

①若AP=AQ，求点P的横坐标；

②若PA=PQ，直接写出点P的横坐标。

3)如图3(b)，△MNE的顶点M，N在抛物线C2上，点M在点N右边，两条直线ME，NE与抛物线C2均有唯一公共点，ME，NE均与y轴不平行，若△MNE的面积为2，设M，N两点的横坐标分别为m,n,求m与n的数量关系。

(a)

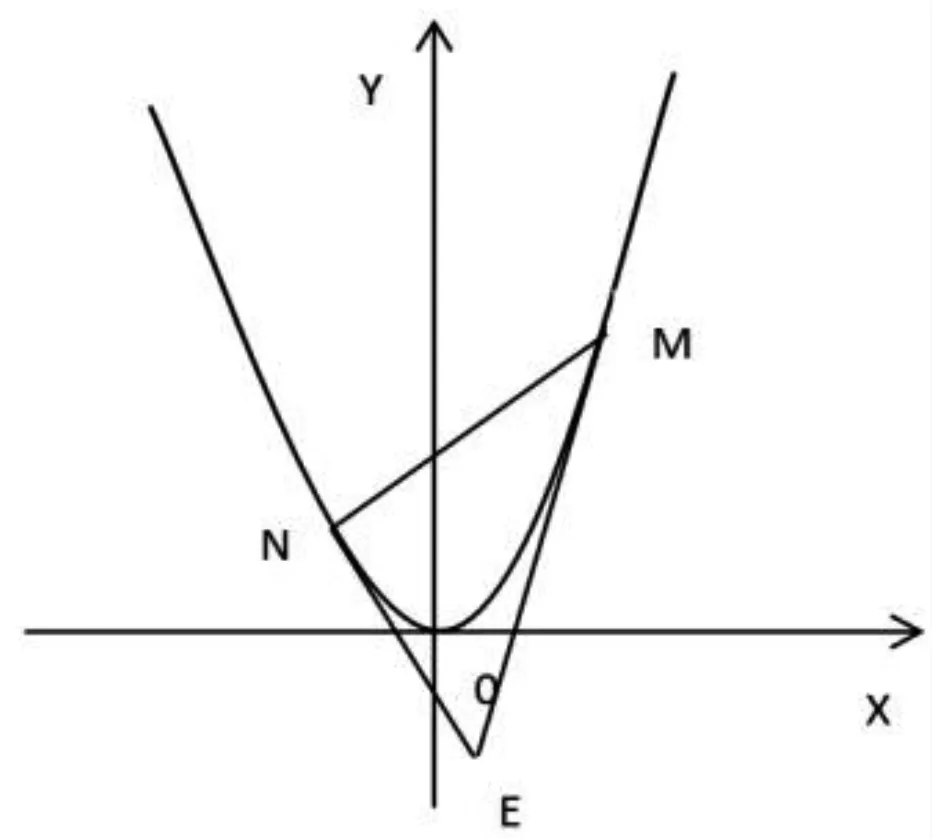
(b)

数学核心素养考查分析：

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养。本题是一道抛物线与函数的综合题，涉及的知识点有抛物线的性质、平移、点的坐标、一次函数等知识，同样也对数形结合思想、直观思维进行考查。

学生解题分析：

此题计算量大，对于学生的数学运算素养要求较高，学生的错误也出于此：

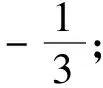
④面积关系出现m-n=-2，造成低级错误。

还有一些学生在直观想象与数学抽象素养犯的错误类型：

①有学生求出直线AD与直线AD′的解析式,但不知道如何进行下一步求出点p的横坐标；

2.6 逻辑推理素养的考查

例：10.观察等式：2+22=23-2；2+22+23=24-2；2+22+23+24=25-2;….已知按一定规律排列的一组数：250，251，252，…，299，2100.若250=a,用含a的式了表示这组数的和是：

A)2a2-2aB)2a2-2a-2 C)2a2-aD)2a2+a

数学核心素养考查分析：

逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养。此题的切入点是需寻找到规律，这对学生平常的积累，以及数学功底要求较高，这道题也涉及到了数学运算素养。

学生解题分析：

逻辑推理素养较强的学生可以较快地利用题目中已知的条件，寻找到规律，并求出这组数的和，而逻辑推理素养较弱的学生虽然找出了2+22+…249=250-2，但并没有推理出2+22+……+2100=2101-2这一式子，因而在答题卡上没有写出正确的答案，可见此类学生的逻辑素养能力有待加强。

在数学运算素养上，有少部分学生会出现此类错误：2101-2-(250-2)=2a2+a或2a2-2a-2.

3 结论与建议

合理将数学核心素养渗透于中考数学试题中能更加有益于全面评价学生，也会进一步促进学生数学核心素养的形成。依据上述研究分析，下面就从教学上提出两点建议：

1)数学课程既要注重基础知识水平提高，也要提升学生核心素养发展水平。

近几年来，核心素养成为一个热点话题，对于素质教育的推进有着积极作用。教书育人这一教学准则也一直是教师强调需要具备的特点，在数学这门学科中的基础知识与基本内容，是学生必备的条件，但从人文价值方面来看，更应该提升数学思维和数学思想这一目标。因此，数学课程既要面向知识也要面向素养。

2)“学而不思则罔，思而不学则殆”，养成良好的思维品质是教学改革中的一个重要课题。

数学核心素养水平的提高需要一个漫长的过程，在重视学生基本知识和基本技能的同时，更应该注重学生思维品质的培养。教师在数学教学中应当教育学生学会透过现象看本质，学会全面地思考问题，养成追根溯源的习惯。