致密油藏水平井压裂裂缝参数优化方法*
姜汉桥 赵玉云,2 陈 强 李俊键 成宝洋 范 桢
(1. 中国石油大学(北京)油气资源与探测国家重点实验室 北京 102249; 2. 浙江理工大学理学院数学系 浙江杭州 310018;3.中石油西部钻探国际工程公司阿克纠宾项目部 新疆乌鲁木齐 830026)
致密油作为一种新兴的非常规油气资源,在美国、加拿大、澳大利亚等地已实现了成功的商业开发[1]。我国的致密油发展较晚,但储量丰富,根据美国能源信息署(EIA)的预测,我国致密油可采资源量达44.8×108t[2-3]。贾承造 等[4]将致密油总结为4个明显标志,其中,孔隙度小于10%、基质覆压渗透率小于0.1 mD、孔喉直径小于1 μm为其最主要的特征。致密油藏储层孔隙度较小、渗透率极低的特性决定了只能采取水力压裂的开采方式。而压裂裂缝参数的优选就成为致密油开发的关键性问题之一。目前已经有许多文章研究水力压裂裂缝的参数优选,但大多针对低渗透油藏[5-6],而对于致密油藏的研究较少。致密油藏由于其储层特性,流体在基质中呈现非线性渗流的特点,而且基质和裂缝存在应力敏感效应,即渗透率随压力的变化而存在动态变化。
本文考虑了致密油藏非线性渗流和应力敏感的特点,在致密油藏非线性渗流数值模拟方法的基础上,研究了水平井单井压裂裂缝的数量、位置分布、长度、开度、方位角等参数对致密油藏衰竭式开采产量的影响规律,并进行了优化设计,形成了基于模拟退火算法的参数优化方法。
1 模型建立
本文模型考虑了致密油藏渗流非线性和应力敏感效应。
1) 非线性渗流。
致密油藏储层致密,基质含有微纳米孔隙,有较强的微尺度效应。目前已有一些文献研究非线性渗流的机理[7-13]。本文采用姜瑞忠 等[7]提出的二参数非线性渗流模型,即
(1)
式(1)中:v为流体的达西速度,kg/m3;μ为流体黏度,mPa·s;K为基质渗透率,mD;p为压力,MPa;ε1和ε2均为非线性系数。
当ξ1=ξ2=0时,式(1)即为传统的达西公式。
2) 应力敏感效应。
研究表明,致密油藏的基质和裂缝有较强的应力敏感性,即基质和裂缝的渗透率随压力的变化而变化,且变化的程度有较大差异,需要用不同的模型来表征[8]。考虑经典的渗透率指数增长模型,即渗透率(K)随压力(p)的变化率与渗透率本身成正比,如下式所示:
(2)
设正比系数为αχ,则有
(3)
两边同时积分,可得
Kχ=Kχ0eαχ(p-pref)
(4)
式(4)中:pref为参考压力,Kχ0为该参考压力下的渗透率,下标χ可取χ=m和χ=f,分别代表基质和裂缝。
3) 模型建立。
对于单相流体,由质量守恒方程,对于任意一个控制体积Ω,考虑岩石和流体的可压缩性时,基于控制体积的流动方程为
(5)
式(5)中:∂Ω为控制体积Ω的边界,n是边界∂Ω上的微元dS的内单位法向量(即指向控制体积内部的单位法向量);φ是岩石的孔隙度,f;ρ是流体在地下的密度,kg/m3;ρs是流体在地面的密度,kg/m3;q是源汇项,kg/s;dσ是Ω的体积微元。
本文考虑微可压缩情形,即基质孔隙度φ和流体密度ρ均与压力呈线性增长关系。
联立式(1)、(4)、(5)可得到致密油藏非线性模型,本文用文献[8]中提到的自动微分的方法来求解该方程组。
2 裂缝参数对产量的影响
研究了压裂裂缝各参数对致密油藏衰竭式开采产量的影响规律,计算中所采用的地层参数和流体参数见表 1。
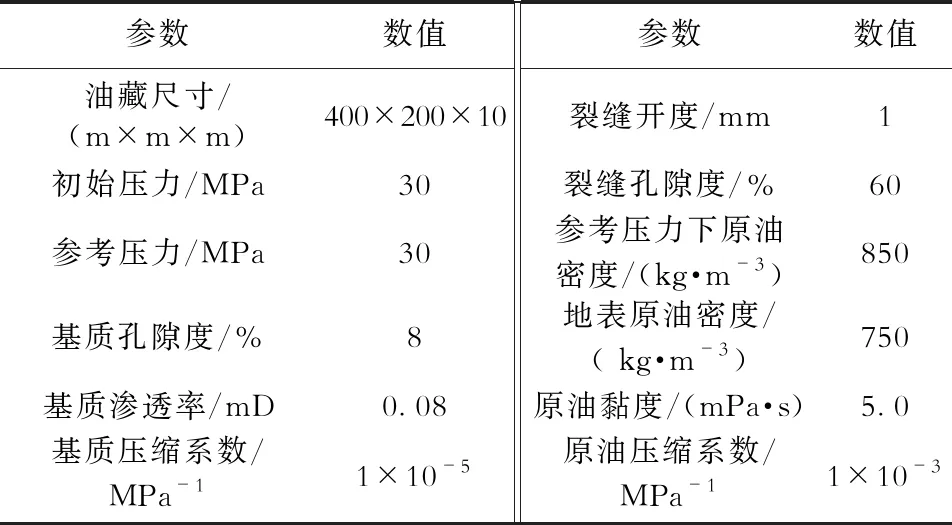
表1 地层参数和流体参数Table 1 Parameters of formation and fluid
2.1 裂缝数量
考虑了6种模型(图1a),模型裂缝条数分别为3、5、7、9、17、33,裂缝沿水平井方向等间距分布,长度均为80 m,开度为1 mm。
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图1所示。对比模拟结果发现,裂缝的数量越多,初始阶段的日产油量越高,得到的累计产油量越多。同时也发现,第100 d的累计产油量与裂缝条数并不成正比,当裂缝数量从9条增加到17条时,得到的累计产油量并没有翻倍,而是增加了约6%。考虑到压裂的成本与裂缝条数成线性关系,因此从经济效益的角度考虑,存在一个裂缝条数的最优值,并不是越多越好。
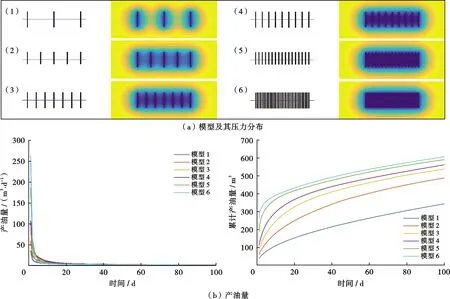
图1 不同裂缝数量的6种模型及其压力分布和产油量对比Fig .1 Six models with different fracture numbers and their pressure distribution and oil production comparison
2.2 位置分布
2.2.1 沿水平井方向的位置分布
考虑了6种模型(图2a),其中模型1裂缝为等间距分布,其余均为非等间距,裂缝长度均为80 m,开度为1 mm。
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图2所示。对比模拟结果发现,裂缝沿水平井方向分布越均匀,在前期的日产油量越高,得到的累计产油量越多。
2.2.2 垂直于水平井方向的位置分布
考虑了6种模型(图3a),裂缝沿水平井方向均等间距分布,其中模型1的5条裂缝在垂直于水平井方向的位置均相同,模型2为垂直于水平井方向交错分布,其余均为随机分布,裂缝长度均为60 m,开度为1 mm。
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图3所示。对比模拟结果发现,裂缝在垂直于水平井方向交错分布,累计产油量越多,模型2与模型1相比,产量提高了5.3%。
考虑了当裂缝条数增加到8条时的情况,模型2与模型1相比,累计产油量增加了14.3% (图 4)。所以交错分布方式可以带来更高的产油效率。
2.3 裂缝长度
考虑了6种模型(图5a),均为5条裂缝,沿水平井方向等间距分布,其裂缝长度分别为20、40、60、80、100和120 m,开度均为1 mm。模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图5所示。对比模拟结果发现,裂缝越长,在前期的日产油量越高,得到的累计产油量越多。

图2 沿水平井方向位置分布不同的6种模型(5条裂缝)及其压力分布和产油量对比Fig .2 Six models(5 fractures) with different positions along the horizontal well and their pressure distribution and oil production comparison

图3 垂直于水平井方向位置分布不同的6种模型(5条裂缝)及其压力分布和产油量对比Fig .3 Six models (5 fractures) with different distributions perpendicular to the horizontal well and their pressure distribution and oil production comparison

图5 不同裂缝长度的6种模型(5条裂缝)及其压力分布和产油量对比Fig .5 Six models(5 fractures) with different fracture lengths and their pressure distribution and oil production comparison
2.4 裂缝方位角
考虑了6种模型(图6a),均为5条裂缝,沿水平井方向等间距分布,其裂缝方位角分别为北偏东0°、15°、30°、45°、60°和75°,裂缝长度均为60 m,开度为1 mm。
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图6所示。对比模拟结果发现,裂缝的方位角越小,得到的累计产油量越多。
2.5 裂缝开度
考虑了6种模型(图7a),均为5条裂缝,沿水平井方向等间距分布,裂缝长度均为80 m,开度分别为0.1、0.5、1、1.5、2和3 mm。

图6 不同裂缝方位角的6种模型(5条裂缝)及其压力分布和产油量对比Fig .6 Six models(5 fractures) with different fracture orientations and their pressure distribution and oil production comparison

图7 不同裂缝开度的6种模型(5条裂缝)及其压力分布和产油量对比Fig .7 Six models(5 fractures) with different fracture apertures and their pressure distribution and oil production comparison
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图7所示。对比模拟结果发现,裂缝开度越大,得到的累计产油量越多。同时也发现,当裂缝开度达到一定程度(如本例的1.5 mm)后,累计产油量的变化很小。
3 基于模拟退火算法的缝网模式优化
以上考虑的裂缝都是等长度的,考虑到压裂的成本与裂缝的长度成正相关,假设裂缝的数量和总长度一定,分别考虑了3种模式的缝网(1-等长型、2-纺锤形、3-哑铃形)和他们的交错形式(4-等长交错型、5-纺锤交错形、6-哑铃交错形),裂缝的数量均为7,总长度均为420 m,如图8a所示。
模拟了100 d的生产动态,油藏压力分布、日产油量和累计产油量如图8所示。可以看出,对比模型1、2、3,外侧长内侧短的哑铃形缝网(模型3),得到的累计产油量最多。同时也发现,交错分布可以有效提高产量。
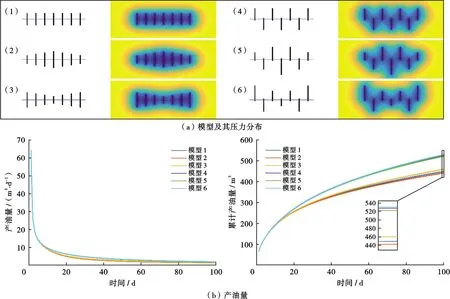
图8 不同缝网模式的6种模型(7条裂缝)及其压力分布和产油量对比Fig .8 Six models(7 fractures) with different fracture network patterns and their pressure distribution and oil production comparison
以上讨论的缝网模式是对称型的,对于非对称的缝网结构,比如图9所示的缝网,是否可以得到更多的产量,很少有文献研究此问题。

图9 非对称的缝网结构Fig .9 Asymmetric fracture network structure
因此,基于模拟退火算法[14],以100 d的累计产油量为最优化目标,对类似图9所示的任意缝网进行了优化研究。该最优化问题可以表述为如下形式:
max 累积产油量
s.t. 裂缝数量为7,总长度为420 m
(6)
即任意改变裂缝的中线点位置和长度,但保持数量和总长度不变,比较模拟得到的累计产油量。考虑到问题的复杂性,本文对裂缝的开度做了限制,假定裂缝开度均为1.5 mm。由第4节知哑铃交错形缝网可以得到较高的产量,本文设置以一定的概率取到哑铃交错形缝网,从而避免优化陷入局部最优。记随机变量Xn表示第n次迭代是否取到哑铃交错形缝网,则有
P(Xn=1)=P(Xn=1|Xn-1=0)×
P(Xn-1=0)+P(Xn=1|Xn-1=1)P(Xn-1=1)
(7)
将上式简记为
Pn=P01(1-Pn-1)+P11Pn-1
(8)
因此可以得到
(9)
由于初值选取非哑铃交错形缝网,因此有P1=0。则在N次迭代中,哑铃交错形缝网出现次数的期望为
(10)
本文取P01=0.7,P11=0.5,迭代6 000次(外部迭代200次,内部迭代30次),则有EN=3 500,结果如图10所示。

图10 模拟退火算法优化过程Fig .10 Simulated annealing algorithm optimization process
得到的最优结果如图11所示,裂缝长度从左至右依次为84、84、30、24、30、84和84 m。优化结果表明哑铃交错形缝网得到的产量更高。

图11 优化得到的最优缝网结构及其压力分布Fig .11 Optimized fracture network and its pressure distribution
基于该优化结果,本文提出一种交错哑铃形压裂方案,即外侧长内侧短的对称型交错压裂方案,以上结果表明,该压裂缝网得到的累计产油量较高。交错哑铃形缝网事实上属于单翼缝组成的缝网模式,单翼缝压裂的可行性在文献[15]中有所提及,因此可以保证交错哑铃形缝网的现场实现。
4 结论
1) 致密油藏压裂裂缝的数量越多、长度越长、方位角越小、开度越大,得到的累计产油量越多。从经济效益的角度考虑,裂缝条数和开度均存在一个最优值,不是数量越多、开度越大越好。
2) 致密油藏压裂裂缝沿水平井方向分布越均匀,在前期的日产油量越高,得到的累计产油量越多。压裂裂缝在垂直于水平井方向交错分布,得到的累计产油量越多。
3) 致密油藏哑铃交错形缝网得到的累计产油量更高,提出了一种外侧长内侧短的交错哑铃形缝网的水平井压裂技术,可为现场压裂方案优选提供借鉴。

