脉动流条件下的圆柱绕流特性研究

曹 兴， 刘宇飞， 于 恒， 孔祥鑫， 李庆领

(青岛科技大学机电工程学院，青岛 266061)

圆柱绕流现象广泛存在于各类实际工程问题之中[1-2]，如海洋工程、测量设备、换热器等。前人对圆柱绕流问题的研究[3-5]主要集中于来流定常流动，但是流体的实际流动过程中存在强烈的非定常性，会产生不同程度的脉动流，如果忽略脉动流对流场的影响，会令研究偏离实际情况。此外，脉动流常用来改变流场与传热特性[6]。宋德福等[7]采用数值方法研究了脉动流下平板壁面的换热；李国能等[8]采用数值模拟方法，研究了平行圆柱体在层流脉动流中的相关特性。但是脉动流条件下的流场中，不仅存在着脉动阻力，而且在垂直来流的展向上会产生较大的升力，同时脉动流在空间上引入了脉动振幅，在时间上引入了脉动频率，导致脉动流下的流场特性非常复杂，使得目前少有对于脉动流条件下圆柱绕流特性的研究[9]。相关研究中，王燕珍[10]对脉动流下圆柱绕流问题进行了研究，发现柱体所受的应力在脉动流条件下更大；Armstrong等[11]在湍流脉动条件下研究了圆柱绕流问题，发现横向分离的减小与旋涡强度的增大影响了锁定范围，但其均未能综合给出脉动频率和无量纲脉动振幅对圆柱绕流尾涡脱落、升阻力系数、旋涡脱落频率等的影响规律。为此采用数值模拟的方法对雷诺数Re=200、脉动流条件下的圆柱绕流特性进行研究，并与相关文献进行对比，分析流体脉动频率与振幅对升、阻力系数以及旋涡脱落频率的影响规律，并对尾涡脱落过程的涡量分布进行研究。

1 数值模拟方法

1.1 物理模型与控制方程

计算区域物理模型如图1所示。由图1可知，计算区域的几何尺寸为20D×30D(D为圆柱直径，m，D=0.1 m)，流体入口边界与圆柱中心的垂直距离为10D，出口边界与圆柱中心的垂直距离为20D，垂直于流向的上下边界到圆柱中心的距离各为10D。

图1 计算区域物理模型Fig.1 Physical model of computational domain

所采用的控制方程为

(1)

(2)

(3)

式中：μ为流体黏度，(N·s)/m2；ρ为流体密度，kg/m3；u为x方向的速度，m/s；v为y方向的速度，m/s；p为压力，Pa。

雷诺数表征流体惯性力和黏性力之比，公式如式(4)所示：

(4)

式(4)中:U为来流速度，m/s。

以水为流动工质，数值计算选用层流模型，Re=200。

1.2 边界条件与数值计算方法

对物理模型的边界条件进行了简化。定义入口为速度入口边界，给定入口速度呈正弦脉动变化，即：

u(t)=um[1+Asin(2πft)]

(5)

式(5)中：u(t)为入口脉动流速度，m/s；t为流动时间，s;um为稳态流速，m/s；f为脉动频率，Hz；A为无量纲脉动振幅，A=A0/D，其中A0为脉动振幅，m。

通过改变脉动频率f和无量纲脉动振幅A(脉动振幅A0与圆柱直径D的比值，A=A0/D)，来改变入口脉动流工况；定义出口为压力出口边界，给定静压和适当的回流条件；圆柱表面设为无滑移不可渗透固体壁面，近壁面处采用标准壁面函数法处理；垂直于流向的上下两边界采用对称边界条件，该边界上各单元节点的变量沿法向的分量为零。

对于压力-速度的耦合选择Coupled算法，动量方程离散采用Quick格式，对于压力项离散采用Standard格式，瞬态项采用二阶隐式格式，时间步长设置为0.002 s。当计算域内所有控制体积的各方程平均绝对残差小于10-5时，认为迭代计算收敛。

1.3 网格划分与独立性验证

计算区域采用结构化网格划分，出于节省计算资源同时提高计算精度的考虑，对圆柱周围区域的网格采取加密处理，而远场区域的网格相对稀疏。

圆柱水动力可以分解为沿流向的阻力和沿法向的升力，将升力Fl和阻力Fd无量纲化，可以分别得到升力系数Cl和阻力系数Cd。

(6)

(7)

式中：Fl为作用于单位长度圆柱上的升力，N/m；Fd为作用于单位长度圆柱上的阻力，N/m。

利用斯特劳哈尔数，可以表示旋涡脱落的快慢程度。

(8)

式(8)中：fv为旋涡脱落频率，Hz；U为来流速度，m/s。

当Re=200时，选用4套不同密度的网格进行独立性测试，由4套网格计算得到Cd时均值、Cl振幅、St，如表1所示。由表1可知，随着网格单元数的增加，Cd时均值、Cl振幅和St均逐渐增大，且变化的幅度均逐渐变缓。由网格2计算出的Cd时均值、Cl振幅和St与网格1计算出的分别相差1.67%、4.17%和5.26%，网格3的计算结果与网格2的计算结果Cd时均值、Cl振幅和St分别相差1.64%、2%和5%，网格4的计算结果与网格3的计算结果Cd时均值、Cl振幅和St分别相差0.81%、0.98%和0.95%。当网格单元数大于网格3的单元数以后，数值计算结果已经相当接近，误差在1.0%以内，计算结果已经满足网格独立性的要求。综合考虑后选用网格3进行计算。网格划分示意如图2所示。

表1 网格独立性验证Table 1 Summary of grids independence checks for simulation

图2 计算区域网格Fig.2 Schematic of the computational grids

1.4 数值计算方法验证

基于文献[12-14]的计算结果，对方法的可靠性与准确性进行验证，结果如表2所示。在定常流条件下，计算得到的Cd时均值与文献[12-14]偏差为5.34%～7.46%，Cl振幅与文献[12-14]偏差为21.54%～31.08%，St的数值与文献[12-14]偏差为5%～16.7%， 偏差均在合理范围之内，证明了本文方法的可靠性。

对9种脉动流工况下圆柱绕流场进行数值计算，结果如表3所示。

表2 计算结果与文献结果对比Table 2 Comparisons between calculated results and literature results

表3 脉动流工况Table 3 The working conditions of pulsating flow

2 数值模拟结果及分析

2.1 典型时刻涡量分布图

图3为不同脉动流工况下，旋涡脱落周期T内等时间间隔的4个典型时刻瞬时涡量图。

图3 不同脉动流条件下圆柱绕流瞬时涡量Fig.3 Vorticity contours of pulsating flowing around a circular cylinder under different conditions

由图3可以看出，在t=0时刻，下涡占据主导地位，分离区域在圆柱上侧近壁面处形成，此时上个旋涡脱落周期形成涡的剪切层还与近壁面黏连；在t=T/4时刻，下涡占据主导地位，新的上涡形成，在下涡的拉拽作用下剪切层断裂；在t=T/2时刻，上涡逐渐开始混合并重新占据主导地位，下涡加速向下游移动；在t=3T/4时刻，上涡混合成一个大涡并占据主导地位，在上涡的作用下，新的下涡形成后剪切层被撕扯断裂离开圆柱表面，此时1个新的旋涡脱落周期完成，如此周而复始。与定常流条件下圆柱绕流流动分离规律不同，脉动流条件下圆柱绕流旋涡的剪切层更薄，分离更快，并且由于速度呈脉动变化，脉动流条件下圆柱绕流的涡量图在1个完整周期内没有明显的对称性。

提高脉动频率f使得尾涡长度变短，旋涡脱落速度加快，混合速度减慢，随着无量纲脉动振幅A逐渐增大，旋涡生成区域越来越靠近圆柱表面，这使得处于主导地位涡的脱落速度减缓，另一侧涡的脱落速度加快。

2.2 脉动频率与脉动振幅对升力系数的影响

图4为无量纲脉动振幅A=1，脉动频率f分别为4、8、10 Hz时升力系数Cl的时间历程曲线。对比图4可以看出，当A不变时，随着f逐渐升高，Cl的振幅逐渐增大。图5为脉动频率f=10 Hz，无量纲脉动振幅A分别为0.2、0.6、1时Cl的时间程曲线。对比图5可以看出，当f不变时，Cl的振幅随着A的增大逐渐增大。与定常流条件下圆柱绕流情况[15]相比可以发现，在相同雷诺数下，脉动流条件下Cl的振幅大于定常流条件下Cl的振幅，说明脉动流的作用使圆柱横向振动增强。

2.3 脉动频率与脉动振幅对阻力系数的影响

当无量纲脉动振幅A=1时，脉动频率f分别为4、8、10 Hz时的阻力系数Cd时间历程曲线如图6所示。由图6可知，A不变的条件下，Cd的振幅随着f的增大而增大。当脉动频率f=8 Hz时，无量纲脉动振幅A分别为0.2、0.6、1时的Cd时间历程曲线如图7所示。由图7可知，f不变的条件下，Cd的振幅随着A的增大而增大。对比图4、图6可知，脉动流条件下圆柱阻力系数的振幅高出升力系数的振幅一个数量级，且阻力系数的变化速率也比升力系数的变化速率更快。与定常流条件下Cd的振幅[15]相比，脉动流条件下Cd的振幅更大，说明圆柱在脉动流条件下会受到更大的流向阻力，使圆柱体流向振动加强。

2.4 脉动频率与脉动振幅对旋涡脱落频率的影响

利用快速傅里叶变换(FFT)方法，可以将升力系数时间历程曲线图转化为频谱图，使时域值转化为频域值，从而得到旋涡脱落频率fv。A=0.6时，三种不同脉动频率下(f=4、8、10 Hz)的升力系数Cl频谱特性如图8所示。图8(a)中，当f=4 Hz时旋涡脱落存在两个主频，主频频率分别为2.1、6.1 Hz；图8(b)中，当f=8 Hz时旋涡脱落存在三个主频，主频频率分别为2.1、6.1、10.1 Hz；图8(c)中，当f=10 Hz时同样存在三个主频， 主频频率分别为2.1、8.1、12.1 Hz。由此可见，脉动流条件下圆柱绕流升力系数频谱图(图8)中同时存在多个不同的主频，其中振幅最大的主频即为旋涡脱落频率fv，且fv的振幅随着脉动频率f的增大而减小，其他主频均为脉动频率f与旋涡脱落频率fv经过相位叠加得到的频率，这可能是由于涡的混合造成的。例如，在图8(b)中，涡脱频率为2.1 Hz，脉动频率为8 Hz，两个频率经过正负相位叠加分别得到了频率为6.1、10.1 Hz的另外两个主频。

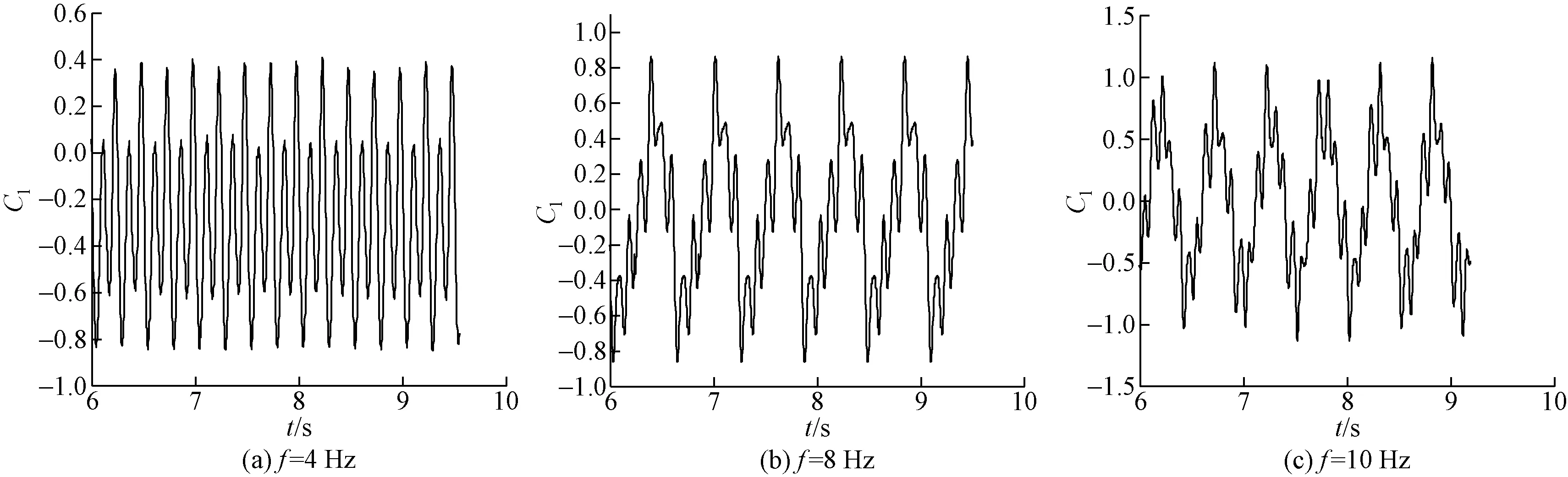
图4 A=1时不同脉动频率下的升力系数时间历程曲线Fig.4 Time-history curve of lift coefficient at different pulsating frequency when A=1

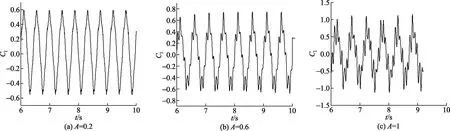
图5 f=10 Hz时不同无量纲脉动振幅下的升力系数时间历程曲线Fig.5 Time-history curve of lift coefficient at different dimensionless pulsating amplitude when f=10 Hz

图6 A=1时不同脉动频率下的阻力系数时间历程曲线Fig.6 Time-history curve of drag coefficient at different pulsating frequency (A=1)

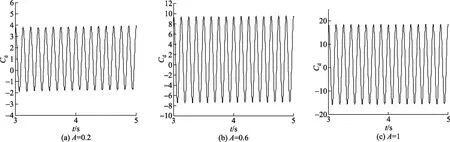
图7 f=8 Hz时不同无量纲脉动振幅下的阻力系数时间历程曲线Fig.7 Time-history curve of drag coefficient at different dimensionless pulsating amplitude (f=8 Hz)

图9 f=10 Hz时升力系数频谱图Fig.9 Frequency spectrogram of lift coefficient (f=10 Hz)

脉动频率为f=10 Hz时，三种不同无量纲脉动振幅(A=0.2、0.6、1)的升力系数频谱特性如图9所示。图9中存在3个主频，其中振幅最大的即旋涡脱落频率fv=2.1 Hz，另外两个频率是由脉动频率f=10 Hz和旋涡脱落频率fv=2.1 Hz相位叠加得到的，分别为8.1、12.1 Hz。由图9还可以看出，频谱图中fv的振幅随着无量纲脉动振幅A的增加而增加。

3 结论

通过研究脉动流条件下，脉动频率和无量纲脉动振幅对圆柱绕流尾涡脱落、升阻力系数、旋涡脱落频率等的影响规律，得出以下主要结论。

(1)当脉动频率增大时，尾涡长度变短，旋涡脱落速度加快；当无量纲脉动振幅增大时，主导涡脱落速度减缓，另一侧涡的脱落速度加快。

(2)随着脉动频率与无量纲脉动振幅的增大，升力系数与阻力系数的振幅均增大，且后者的振幅比前者的振幅高一个数量级，变化速率后者也更快。

(3)升力系数频谱图存在多个主频，其中振幅最大的频率为旋涡脱落频率，其余频率均是由脉动频率与旋涡脱落频率相位叠加的结果；随着脉动频率的增加，或无量纲脉动振幅的减小，旋涡脱落频率的振幅减小。